柔性微动机构是一种靠各构件的变形来输出力或位移的机构[1-2]。现代科学技术的发展,使得柔性机构在微机电、微加工、微制造、微装配、纳米技术、航空航天和生物工程[3-8]等微观领域得到广泛应用。刚度是影响柔性微动机构动态性能和末端定位精度的重要因素,因此刚度是评价柔性微动机构的重要指标。
现有的柔性微动机构分析方法主要有伪刚体模型法[9-11]和结构矩阵法[12-13]。伪刚体模型法由Howell和Midha[14]最先提出,其基本思想是刚体替换法,将柔性机构等效简化为相应的刚性机构模型,再沿用成熟的刚性体理论对柔性机构的刚度进行分析。该方法计算简单,但伪刚体模型不唯一,刚体柔体之间有较大差别,在复杂力作用下,变形不仅发生在一维方向上,因此计算精度相对较低。结构矩阵法是一种扩展的伪刚体模型法,考虑柔性运动副的变形,对于柔性运动副间的连杆部件作为刚体考虑,利用刚柔单元变形协调方程、力平衡方程、坐标变换到整体坐标系下计算机构刚度。精度比伪刚体模型高,但变形协调难求解,计算量大。
基于以上方法的特点,提出一种求解柔性微动机构新方法——传递矩阵法。将柔性微动机构模块化,各子单元视为柔体,分别求解其传递矩阵,利用相邻子单元结点力与位移的关系将各子单元传递矩阵组合,由力平衡求解整个机构的刚度。该方法避免了变形协调方程及全局坐标系的变换,求解简单,具有递推性,利于编程,且考虑了各子单元的变形,求解结果更精确。以一种柔性杠杆放大机构为例,推导了其刚度的求解过程,并与ANSYS分析结果对比,证明了此方法的精确性。
1 传递矩阵法 1.1 基本原理选取的任一梁单元,如图 1所示。传递矩阵表示左结点力Fl、位移ul与右结点力Fr、位移ur的矩阵关系。结点力包括轴向力Fx、剪切力Fy、弯矩M,结点位移包括轴向位移ux、横向位移uy以及转角α。定义传递矩阵的传递方向由左向右,如图 1中箭头所示。

|
| 图 1 梁单元结点力与位移 Fig. 1 Beam element node force and displacement |
单元从左 (l) 端到右 (r) 端的关系为
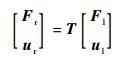
|
(1) |
式中:Fi=[Fxi Fyi Mi]T,i=l, r;ui=[uxi uyi αi]T; T为传递矩阵,文献[15]根据力平衡及虚功原理求解了传递矩阵的公式为

|
(2) |
其中:
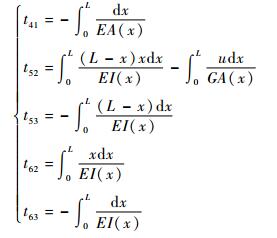
|
(3) |
L为梁的长度;E为弹性模量; G为剪切模量;u为应力分布不均匀系数,当截面为矩形时取u=1.2;A (x) 为截面剪切面积函数;I (x) 为惯性积函数。
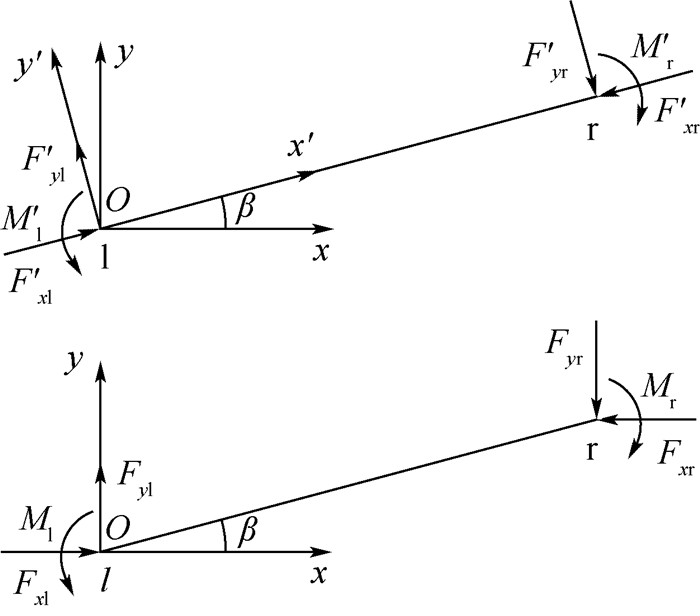
1.2 传递矩阵坐标变换在单元坐标系下,传递矩阵可根据式 (2) 求得。为了便于建立结点力平衡,需要将各子单元统一到结构坐标系中。如图 2所示,当梁单元绕l端旋转角度β(逆时针为正) 时,单元坐标系Ox′y′下的结点力为Fxi′、Fyi′、Mi′ (i=l, r);结构坐标系Oxy下的结点力为Fxi、Fyi、Mi(i=l, r)。两者之间的关系如下:
|
| 图 2 梁单元旋转变换 Fig. 2 Rotation transform of beam element |
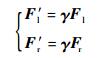
|
(4) |
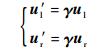
|
(5) |
式中:γ为旋转矩阵,其定义为

|
在单元坐标下传递矩阵关系为

|
(6) |
将式 (4)、式 (5) 代入式 (6) 可得
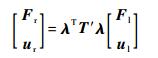
|
(7) |
式中: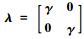
则梁单元在结构坐标系下传递矩阵为
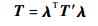
|
(8) |
柔性杠杆放大机构如图 3所示,该机构根据杠杆原理设计,包括固定平台、驱动器、柔性铰链、弹性移动副、杠杆以及连杆。驱动器1产生驱动位移,经过弹性移动副2、柔性铰链3、连杆4、柔性铰链5传递变形。柔性铰链6相当于杠杆支点,通过杠杆7将位移放大,再通过柔性铰链8、连杆9、柔性铰链10在弹性移动副11上输出位移。支链3、4、5与支链8、9、10结构相同,其作用是使整个机构不产生过约束。

|
| 图 3 柔性杠杆放大机构示意图 Fig. 3 Schematic diagram of flexible lever magnifying mechanism |
动力臂与阻力臂的比值决定了柔性杠杆放大机构的放大倍数,即杠杆7的长度决定其放大倍数。利用伪刚体模型法求解时,将杠杆7视为刚体绕支点的转动,输入输出为线性关系,但杠杆7末端需要克服阻力,因而会产生挠度,过长会导致其刚度变小而发生弯曲,因此合理的构建模型,选取杠杆7的长度使整个机构刚度最小是设计此机构的关键。
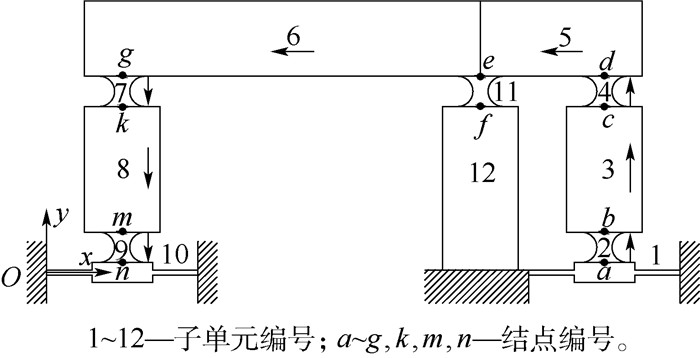
2.2 子单元刚度建模将柔性杠杆放大机构划分单元,从图 4可以看出,共有3种单元,分别为弹性移动副、柔性梁以及柔性铰链。箭头表示传递矩阵的传递方向。图 5为柔性杠杆放大机构参数模型。
|
| 图 4 柔性杠杆放大机构单元划分 Fig. 4 Element partition of flexible lever magnifying mechanism |

|
| 图 5 柔性杠杆放大机构参数模型 Fig. 5 Parameter model of flexible lever magnifying mechanism |
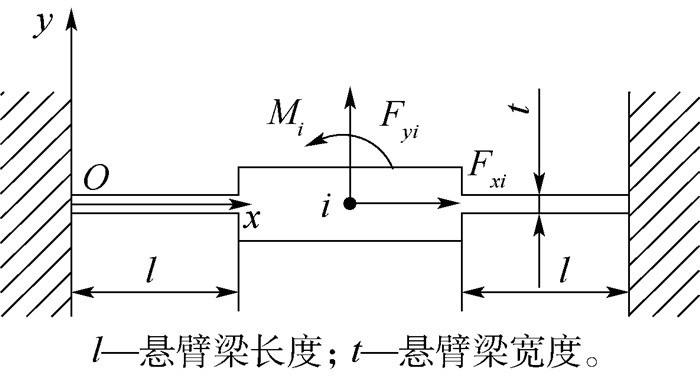
弹性移动副单元的受力方向及结构尺寸如图 6所示。
|
| 图 6 弹性移动副 Fig. 6 Flexible prismatic pair |
弹性移动副i点力与位移关系为

|
(9) |
式中:Kp为弹性移动副的刚度矩阵[16],其定义为
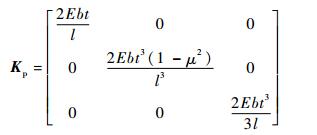
|
其中:b为弹性移动副z轴方向宽度;μ为泊松比。
单元1和单元10为弹性移动副,因此,可以得到
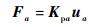
|
(10) |
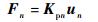
|
(11) |
式中:Kpa=Kp(t1, l1),下标a为单元1中结点a;Kpn=Kp(t7, l7),下标n为单元10中结点n;ua为结点a位移;un为结点n位移。
2.2.2 柔性梁传递矩阵图 7为柔性梁单元,传递矩阵方向如箭头所示。求解积分式 (3) 即可得到柔性梁单元的传递矩阵Tl。

|
| 图 7 柔性梁单元 Fig. 7 Flexible beam element |
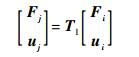
|
(12) |
式中:Tl中的元素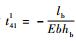
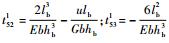
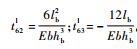
单元3、5、6和8为柔性梁单元,根据图 4中传递矩阵的方向对各个子单元进行坐标变换。
单元3传递矩阵为
T3=λ(90°)T Tl(l2, h1)λ(90°)
单元5传递矩阵为
T5=λ(180°)TTl(l4, h2)λ(180°)
单元6传递矩阵为
T6=λ(180°)TTl(l5, h2)λ(180°)
单元8传递矩阵为
T8=λ(-90°)TTl(l6, h3)λ(-90°)
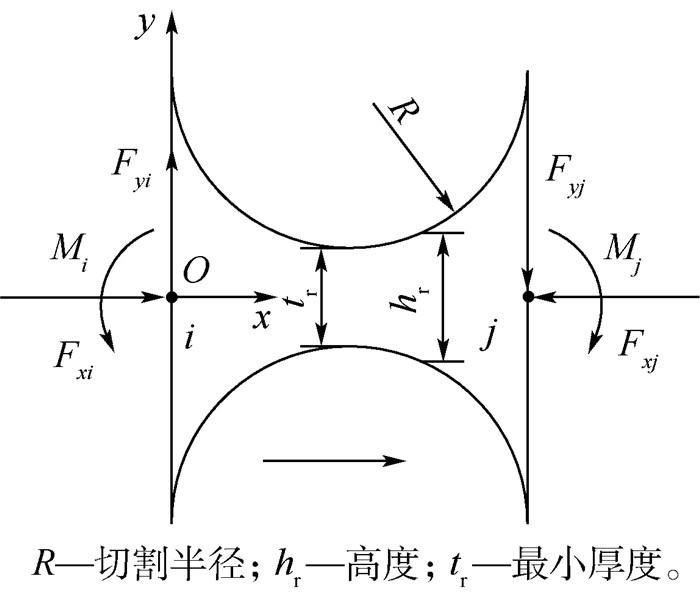
2.2.3 柔性铰链传递矩阵柔性铰链单元的传递矩阵方向及结构尺寸如图 8所示。
|
| 图 8 柔性铰链 Fig. 8 Flexible hinge |
柔性铰链右节点j与左结点i传递矩阵关系为

|
(13) |
柔性铰链为变截面梁,需要通过积分求得传递矩阵,坐标系如图 8所示,其可变高度hr函数为
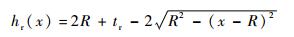
|
(14) |
代入求解积分式 (3) 即可得到柔性铰链单元的传递矩阵Tr。
Tr中的元素

|
单元2、4、7、9为柔性铰链单元,根据图 4中传递矩阵的方向对各个子单元进行坐标变换。
单元2传递矩阵为
T2=λ(90°)TTr(R1, t2)λ(90°)
单元4传递矩阵为
T4=λ(90°)TTr(R2, t3)λ(90°)
单元7传递矩阵为
T7=λ(-90°)TTr(R4, t5)λ(-90°)
单元9传递矩阵为
T9=λ(-90°)TTr(R5, t6)λ(-90°)
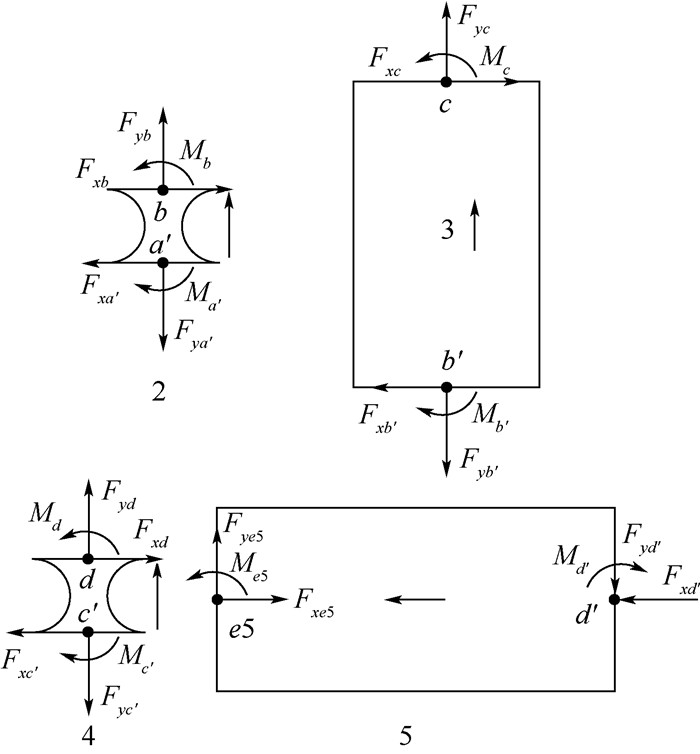
2.3 力平衡建立支链2、3、4、5受力分析如图 9所示。
|
| 图 9 子单元2、3、4、5受力分析 Fig. 9 Force analysis of subunit 2, 3, 4, 5 |
在各子单元中传递矩阵分别为
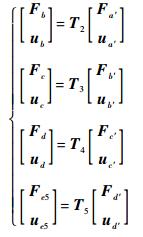
|
(15) |
因为b点力与b′点力为作用力与反作用力,位移连续,则Fb=Fb′,ub=ub′。
同理Fc=Fc′,uc=uc′,Fd=Fd′,ud=ud′。
因此
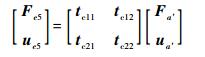
|
(16) |
式中: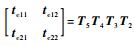
同理支链6、7、8、9为
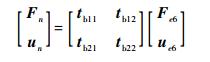
|
(17) |
式中: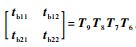
将柔性铰链单元11对e点的作用等效为力Fe,e点力平衡得
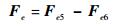
|
(18) |
e点位移连续得

|
(19) |
因此,
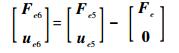
|
(20) |
对于柔性铰链单元11

|
(21) |
式中:kr为柔性铰链一端固定时刚度[17]。
输入点a力平衡得

|
(22) |
式中:Fa为作用在弹性移动副a点的力;Fa′为作用在柔性铰链单元2a′点的力;F=[0 Fy 0]T为作用于弹性移动副的外力。
由式 (10)、式 (11)、式 (16)、式 (17)、式 (20)~式 (22) 联立可以求得

|
(23) |
式中:

|
刚度矩阵的逆矩阵为其柔度矩阵,因此输出位移un与输入力F关系为

|
(24) |
式中:C为机构的柔度矩阵,定义

|
由式 (24) 可得到弹性移动副a输入力Fy与末端y向输出位移uyn关系式为
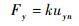
|
(25) |
式中: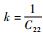
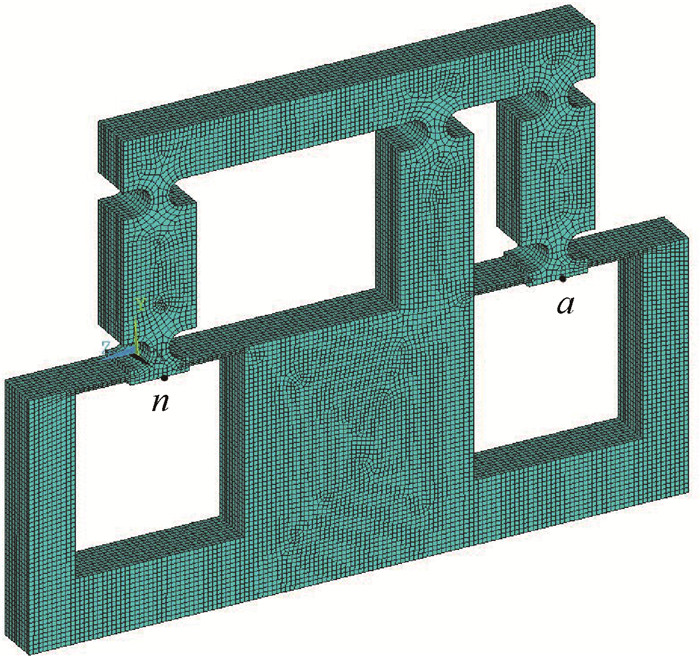
分析比较传递矩阵法与有限元分析之间的误差。运用ANSYS14.0建立柔性杠杆放大机构模型进行刚度研究,选择三维20节点实体单元Solid95,设定柔性杠杆放大机构的材料为60Si2Mn,材料弹性模量E=206 GPa,泊松比μ=0.27,剪切模量G=79 GPa。假设结构参数为:厚度b=10 mm,t1=t7=1 mm,l1=l7=11.5 mm,l2=l6=27 mm,l4=26.5 mm,l5=50.5 mm,h1=16 mm,h2=11 mm,h3=16 mm,Ri=3 mm (i=1, 2, …, 5),ti=4 mm (i=2, 3, …, 6)。建立柔性杠杆放大机构有限元模型,网格划分如图 10所示。
|
| 图 10 柔性杠杆放大机构ANSYS网格划分 Fig. 10 ANSYS mesh generation of flexible lever magnifying mechanism |
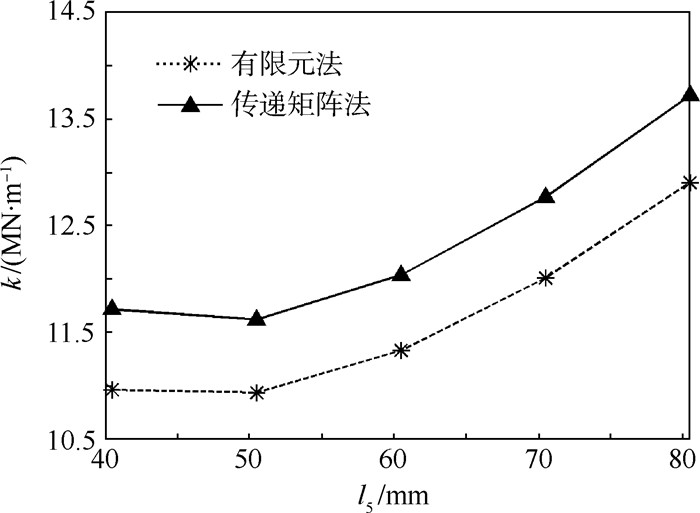
约束固定平台,在输入弹性移动副a点施加力Fy=100 N。在输出弹性移动副n点提取输出位移uyn。因此通过分析所得机构刚度为k=Fy/uyn。通过MATLAB计算式 (23) 和式 (25) 求解传递矩阵法的刚度。改变l5的尺寸,得到不同的机构参数下的有限元分析值及传递矩阵值。其误差对比结果如表 1所示,可以得到其误差在6.4%以内,表明传递矩阵法是精确的。由图 11可以看出,有限元法与传递矩阵法刚度变化规律是一致的,因为考虑了各个单元的变形,与实际情况是相符合的。由此可通过传递矩阵法求解刚度的最小值,使其在相同的输入力的情况下,输出位移最大。
| l5/mm | 刚度/(MN·m-1) | 误差/% | |
| 有限元法 | 传递矩阵法 | ||
| 50.5 | 10.931 9 | 11.618 2 | 6.278 28 |
| 60.5 | 11.326 9 | 12.034 7 | 6.248 46 |
| 70.5 | 12.008 9 | 12.768 9 | 6.329 08 |
| 80.5 | 12.903 9 | 13.273 1 | 6.348 12 |
|
| 图 11 有限元法与传递矩阵法关系曲线 Fig. 11 Relation curves of finite element method and transfer matrix method |
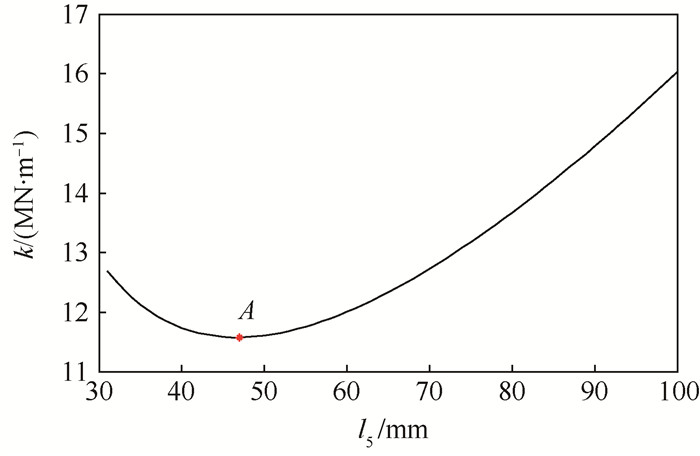
例如本文中的柔性杠杆放大机构模型,传递矩阵法刚度k与l5的关系曲线如图 12所示,A点即为刚度最小值点,此时l5为47 mm,相对应的刚度值为11.578 6 MN/m。
|
| 图 12 刚度k与l5的关系曲线 Fig. 12 Relation curve of stiffness k and l5 |
传递矩阵法求解结果大于有限元分析结果,可能原因为结构力学、弹性力学梁理论是建立在一定假设条件下的,为理想变形,在求解过程中忽略了细节变形,如求解弯矩时忽略轴向变形等;传递矩阵法将机构模块化,然后将各子单元组合,忽略了各子单元之间的变形;利用有限元求解的为三维的变形,而本文求解为二维平面内变形,因此产生偏差,并且有限元为近似的数值解,因此与真实值也有一定偏差。
4 结论1) 传递矩阵法将柔性微动机构划分为若干子单元,考虑各个子单元的轴向力、剪切力、弯矩变形。根据子单元传递矩阵的传递关系及力平衡求解整体机构刚度。避免了刚柔单元的位移协调方程及将各单元转换到整体坐标系,减少了计算工作量,且具有递推性,利于编程。
2) 以柔性杠杆放大机构为例,将有限元法分析结果与传递矩阵法分析结果相对比,误差在6.4%以内,且刚度的变化规律是一致的,证明了此方法的精确性,与实际情况相符。因此可通过传递矩阵法求解柔性杠杆放大机构刚度的最小值,使其在相同的输入力的情况下,输出位置最大。对柔性杠杆放大机构参数设计提供了理论依据。同时,此方法同样适用于其他柔性微动机构的刚度及运动学分析。
| [1] |
于靖军, 郝广波, 陈贵敏, 等. 柔性机构及其应用研究进展[J].
机械工程学报, 2015, 51 (13): 53–68.
YU J J, HAO G B, CHEN G M, et al. State-of-art of compliant mechanisms and their applications[J]. Journal of Mechanical Engineering, 2015, 51 (13): 53–68. (in Chinese) |
| [2] |
宫金良, 裴童, 张彦斐. 面向高精度放大比的微动机构设计与实现[J].
北京理工大学学报, 2015, 35 (7): 691–696.
GONG J L, PEI T, ZHANG Y F. Parameter design method of micro-motion mechanism targeting for precise displacement amplification ratio[J]. Transactions of Beijing Institute of Technology, 2015, 35 (7): 691–696. (in Chinese) |
| [3] |
赵荣丽, 陈新, 李克天. 双柔性平行六连杆微动平台结构的设计及测试[J].
光学精密工程, 2015, 23 (10): 2860–2869.
ZHAO R L, CHEN X, LI K T. Design and experiments of micro motion platform based on a pair of flexible parallel six-bar linkages[J]. Optics and Precision Engineering, 2015, 23 (10): 2860–2869. (in Chinese) |
| [4] | HAO G B, KONG X W. A novel large-range XY compliant parallel manipulator with enhanced out-of-plane stiffness[J]. Journal of Mechanical Design, 2012, 134 (6): 061009. DOI:10.1115/1.4006653 |
| [5] | SARAJILIC E, YAMAHATA C, CORDERO M, et al. Three-phase electrostatic rotary stepper micromotor with a flexural pivot bearing[J]. Journal of Microelectromechanical System, 2012, 19 (2): 338–349. |
| [6] |
陈兴林, 刘川, 刘杨, 等. 精密运动平台宏微控制系统的设计[J].
中南大学学报 (自然科学版), 2013, 44 (6): 2318–2323.
CHEN X L, LIU C, LIU Y, et al. Dual-stage actuator control system design for precision motion platform[J]. Journal of Central South University (Science and Technology), 2013, 44 (6): 2318–2323. (in Chinese) |
| [7] |
胡俊峰, 徐贵阳, 郝亚州. 一种新型空间微操作平台的设计和性能[J].
机械设计与研究, 2014, 30 (1): 42–46.
HU J F, XU G Y, HAO Y Z. Design and characteristics of a novel spatial micro-manipulation stage[J]. Machine Design and Research, 2014, 30 (1): 42–46. (in Chinese) |
| [8] | YU J J, HU Y D, BI S S, et al. Kinematics feature analysis of a 3 DOF in-parallel compliant mechanism for micro manipulation[J]. Chinese Journal of Mechanical Engineering, 2004, 17 (1): 127–131. DOI:10.3901/CJME.2004.01.127 |
| [9] | YU Y Q, FENG Z L, XU Q P. A pseudo-rigid-body 2R model of flexural beam in compliant mechanisms[J]. Mechanism and Machine Theory, 2012, 55 (9): 19–33. |
| [10] |
邱丽芳, 霍明磊, 李威. 六杆柔顺机构的伪刚体模型[J].
北京科技大学学报, 2013, 35 (5): 682–686.
QIU L F, HUO M L, LI W. Pseudo-rigid-body model of a six-bar full-compliant mechanism[J]. Journal of University of Science and Technology Beijing, 2013, 35 (5): 682–686. (in Chinese) |
| [11] |
李茜, 余跃庆, 常星. 基于2R伪刚体模型的柔顺机构动力学建模及特性分析[J].
机械工程学报, 2012, 48 (13): 40–48.
LI Q, YU Y Q, CHANG X. Dynamic modeling and analysis of compliant mechanisms based on 2R pseudo-rigid-body model[J]. Journal of Mechanical Engineering, 2012, 48 (13): 40–48. (in Chinese) |
| [12] |
于靖军, 毕树生, 宗光华. 空间全柔性机构位置分析的刚度矩阵法[J].
北京航空航天大学学报, 2002, 28 (3): 323–326.
YU J J, BI S S, ZONG G H. Stiffness matrix method for displacement analysis of fully spatial compliant mechanisms[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28 (3): 323–326. (in Chinese) |
| [13] |
艾青林, 黄伟锋, 张洪涛, 等. 并联机器人刚度与静力学研究现状与进展[J].
力学进展, 2012, 42 (5): 583–592.
AI Q L, HUANG W F, ZHANG H T. Review of stiffness and statics analysis of parallel robot[J]. Advances in Mechanics, 2012, 42 (5): 583–592. DOI:10.6052/1000-0992-11-073 (in Chinese) |
| [14] | HOWELL L L, MIDHA A. A method for the design of compliant mechanisms with small-length flexural pivots[J]. Transactions of the ASME, Journal of Mechanical Design, 1994, 116 (1): 280–290. DOI:10.1115/1.2919359 |
| [15] |
李青宁. 变截面杆元传递矩阵法[J].
西安建筑科技大学学报, 2001, 33 (1): 18–23.
LI Q N. The transfer matrix method of bar elements with variable cross-section[J]. Journal of Xi'an University of Architecture & Technology, 2001, 33 (1): 18–23. (in Chinese) |
| [16] |
杨春辉. 平行板型柔性移动副的刚度计算及分析[J].
现代制造工程, 2013 (12): 30–33.
YANG C H. The stiffness design calculation and analysis of parallel plate flexible prismatic pair[J]. Modern Manufacturing Engineering, 2013 (12): 30–33. DOI:10.3969/j.issn.1671-3133.2013.12.008 (in Chinese) |
| [17] |
吴鹰飞, 周兆英. 柔性铰链的设计计算[J].
工程力学, 2002, 19 (6): 136–140.
WU Y F, ZHOU Z Y. Design of flexure hinges[J]. Engineering Mechanics, 2002, 19 (6): 136–140. (in Chinese) |



