2. 北京航空航天大学 自动化科学与电气工程学院, 北京 100083
2. School of Automation Science and Electrical Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
变体飞行器通常是依据飞行任务模式、飞行参数和外部环境的变化而主动调整外形结构,从而改善气动性能和操纵能力,这种变形可以达到扩大飞行包线和适应不同飞行性能的目的[1]。近些年,各国的学者针对其结构、气动和控制等方面展开了深入的研究[2-5]。
变体飞行器控制系统的研究热点主要集中在以下2个方面[6-8]:① 机体变形控制系统的设计;② 保证变形过程中的稳定性和飞行性能的控制系统设计。第② 点是本文的主要研究问题,针对变形过程中的模型运动建模与姿态控制,众多学者已开展一系列的研究[9-14]。文献[10]由时变极点的概念推导变后掠快速变形的微型飞行器纵向模型,发现变形时间和飞行器动态特性有相近的时间尺度,所以必须考虑变形引起的时变特性。文献[11]对Z型翼飞行器建立纵向多体动力学模型,数值模拟了机翼折叠动态过程的气动特性,研究了重心和气动特性变化共同对变形动态特性的影响。文献[12]则研究大尺度变形的建模与控制问题,并对纵向系统设计镇定控制器。
综合上述研究表明,在变形过程中,外形和气动参数的变化,变形所引起的附加惯性载荷,均对稳定飞行带来严重影响,变体飞行器是一个依赖于外形结构的复杂时变非线性系统,其稳定性和控制器设计需要考虑。对于时变非线性系统,一般采用自适应控制、切换控制等方法。文献[13]将参数变化和耦合视为模型的时变参数和干扰; 构建的L1横侧向控制律能够对控制信号中的高频振荡进行有效抑制。虽然增益调参控制在当前控制工程中广泛应用,但对于参数快速变化的变体飞行器很难适用。
线性变参数 (LPV) 系统模型及其鲁棒控制是解决办法之一,因此考虑此控制系统稳定性问题[14-15]。文献[16]考虑一类折叠翼,建立系统的LPV模型,设计鲁棒H∞控制器并保证变形过程的稳定性。但是,上述文献对于变体飞行器LPV模型的构建过程并不详细,LPV建模本身就是一个较为复杂的任务。除此之外,LPV方法的几点不足限制了其在航空工程领域的大范围推广应用。一是其无法保证设计问题对应的线性矩阵不等式 (LMI) 可解,也即无法保证完成姿态控制系统设计,这一问题在参数大范围变化时更为突出。二是要求被控对象的参数缓慢变化,这点与传统的增益调参方法相同。在工程设计中,参数变化速率难以定量描述,而且对于强调多任务、高机动的变体飞行器而言,其参数变化已不再缓慢。
近些年,部分学者利用切换系统的模型对飞行器在包线内的运动特性进行描述,取得一定的研究成果[17-19]。段广仁和王好谦[17]对倾斜转弯导弹的自动驾驶仪应用多模型切换控制方法。Hou等[18-19]利用具有局部重叠特性的切换多胞系统描述了大包线内飞行器的运动,结合Lyapunov函数与平均驻留时间的方法保证了系统的全局稳定性。以上方法为变体飞行器的建模与控制提供了新的思路,但线性切换系统模型有其局限性,一方面,切换系统固有的离散信号与实际系统运动特性不符,另一方面,切换系统的稳定性分析通常在任意切换律下展开,脱离了实际系统的切换特征,给系统的分析与综合带来了很大的保守性。为解决上述问题,本文考虑建立变体飞行器链式平滑切换系统模型,既能简洁、合理地反映变体飞行器的运动特性,又能兼顾其连续过渡的变形特征,且为降低设计的保守性提供了基础。
1 LPV变体飞行器建模变体飞行器Firebee BQM-34A/S是美国NextGen公司设计的一款变体技术验证机,在飞行过程中,机翼后掠角能够在15°~60°之间连续变化,实现“巡航”和“高速”构型间的切换。纵向短周期非线性动力学模型如下:

|
(1) |
其中:XδT为发动机推力系数; δT为油门; Q为动压;S为飞行器参考面积;cA为平均气动弦长;α为飞行器迎角;δe为飞行器的升降舵;CL0、CLα、CLδe、Cm0、Cmα、Cmδe分别为对应的气动力及气动力矩系数;g为重力加速度;mw为飞行器质量;xw为飞行器质心位置;θ为飞行器俯仰姿态角。解算出对应的平衡点飞行状态θe、αe及控制输入量δTe、δee。然后在该平衡点附近采用雅可比线性化方法,可以列出变体飞行器纵向运动的小扰动线性化方程数值形式,再将变形造成的广义干扰项惯性力wZ和惯性力矩wM处理为时变有界外部干扰w (t),则可以得到变体飞行器各典型构型在小扰动情况下对应的线性状态空间模型如式 (2) 所示:
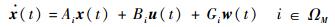
|
(2) |
式中:x (t)=[Δh ΔV Δα Δθ Δq Δδe]T为系统状态,其中Δα=α-αe,其他参数同理;u (t)=[ΔuδT Δuδe]T为控制输入;w (t) 为干扰输入;有限集合ΩM={M15, M20, …, M60}为系统子构型指标集,且子构型M15对应后掠角15°,子构型M20对应后掠角20°。
变体飞行器构型参数如表 1所示。
| 形态 | ν/(°) | Jyf/(kg·m2) | mT/kg | mw/kg | ma/kg | xw/m | xa/m | B/m | S/m2 | cA/m |
| 巡航 | 15 | 3 107.5 | 907.8 | 272 | 26.36 | 0 | -3.2 | 6.803 3 | 4.362 1 | 0.710 1 |
| 高速 | 60 | 3 107.5 | 907.8 | 272 | 26.36 | -0.607 2 | 3.065 6 | 3.84 | 6.079 2 | 1.911 7 |
| 注: ν—后掠角; Jyf—俯仰转动惯量; mT—总重; ma—配重;xa—配重质心位置; B—翼展。 | ||||||||||
其中ν0=15°为巡航构型对应的机翼后掠角。若选定ν=π/12,π/9,5π/36…,π/3共10个值作为计算参考点,参考点取得越多,则建模精度越高,其计算量就越大,于是参考点的选取需要综合考虑上述2个因素。
对不同构型的气动导数利用ANSYS软件仿真得到,利用MATLAB对数据进行差值拟合,得到如下关系式:

|
(3) |
对非线性模型采用雅可比线性化的方法,则得到LPV模型。
步骤1 对式 (2) 选取的15个不同工作区域平衡点,这里采用后掠角ν作为平衡点的选取。
步骤2 不同平衡点可求解出状态量的稳态解,则得到10个不同的小扰动线性模型。
步骤3 将得到的10个小扰动线性模型数值拟合,即可构建变体飞行器纵向短周期运动LPV模型:

|
(4) |
式中:状态变量只取迎角和俯仰角速率,x=[Δα Δq]T;控制变量u=Δδe。

|
将ν的取值区间Θ划分为J个子区间,对应于J个子区间,可得到J个LPV子系统,定义切换律,则得到开环切换LPV系统为

|
(5) |
为便于书写,将子系统系数矩阵Aj(ν)、Bj(ν) 表示成Aj和Bj,下文中所有参数依赖的矩阵或矩阵变量均采用类似表达。
定义1 对于上述切换系统,更进一步强化条件,即给定子系统指标集合j={p, q, r, …, ω},如果系统存在子系统指标序列ξ:p→q→r→…→ω,使得任意切换信号σc(t):[0, t)→j的切换序列可分解为ξ的若干个子序列或逆序子序列,则称j为关于指标序列ξ的链式切换信号。下文j=σM(t)。
考虑到变体飞行器在各构型之间是平滑过渡的,即认为切换系统在各子系统之间进行连续的平滑切换,将变形飞行近似为如下的平滑切换系统模型:

|
(6) |
式中:θi(t)∈[0, 1], i∈ΩM为子系统权值;σM+(t) 为切换律σM(t) 在t时刻之后将要激活的系统子构型指标,若σM(tf)=i,则有σM+(tf)=i+或σM+(tf)=i-。对于给定的切换信号σM(t):[0, TM)→ΩM,以tk, k∈R+表示σM(t) 的第k个切换时刻,则平滑切换系统模型中的子系统权值应满足
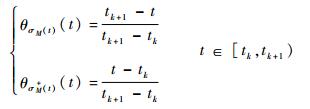
|
(7) |
进一步考虑切换信号σM(t),由于变形过程中后掠角具有连续变化特性,系统在子构型指标集ΩM中不可能任意切换,由链式切换律定义和σM(t) 的运行特点可知,σM(t) 是关于序列ξM:M15→M20→…→M60的链式切换信号。
3 控制器设计 3.1 鲁棒平滑切换镇定控制器设计定义2 如果切换系统式 (2) 具有以下性质:
1) 当w (t)≡0时,系统是全局一致渐近稳定的。
2) 对于给定的常数γ>0,在零初始条件且u (t)≡0的情况下,对于∀w(t)∈L2[0, ∞),满足:

|
(8) |
则称切换系统 (1) 具有H∞性能指标γ。
定义3 对于给定的切换律σ(t) 及任意的T>t≥0,令Nσ(t, T) 表示σ(t) 在区间[t, T) 上的切换次数,如果存在非负整数N0和正数τa满足

|
(9) |
则称σ(t) 具有平均驻留时间τa,不失一般性,取N0=0。
定义4 对于给定的切换律σ(t):[0, +∞)→Ω及任意的T>t≥0,令Nσi(t, T), i∈Ω表示σ(t) 在区间[t, T) 上第i个子系统被激活的次数,令Ti(t, T)(i∈Ω) 表示在区间[t, T) 上第i个子系统被激活的总时间,如果存在非负整数N0i和正数τai满足

|
(10) |
则称σ(t) 具有模型依赖平均驻留时间τai,不失一般性,取N0i=0。
若为系统设计形如u (t)=Kjx (t), j=σM(t) 的切换状态反馈控制器,则有如下定理结论。
定理1 考虑变体飞行器链式平滑切换系统式 (6),令x (0)=0,如果对于∀i∈ΩM,以及给定的常数λi>0,μi>1,存在一组正定矩阵Pi>0,适维矩阵Li和常数γ>0,εi>0,使得下述线性矩阵不等式组成立:
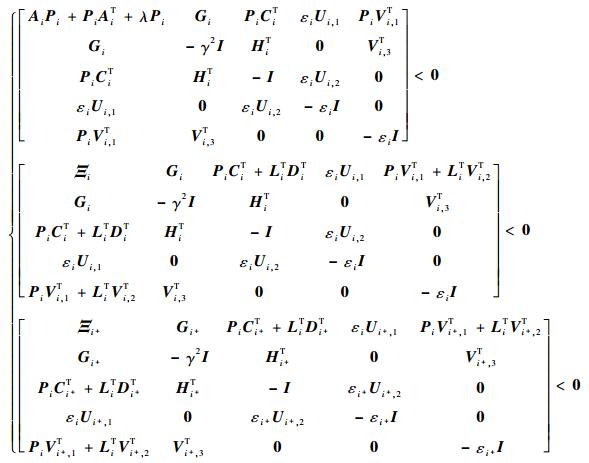
|
(11) |

|
(12) |

|
(13) |
式中:Ξi=AiPi+PiAiT+λiPi+BiLi+LiTBiT;Ξi+=Ai+Pi+PiAi+T+λiPi+Bi+Li+LiTBi+T,且系统在链式切换信号σM(t) 下的构型依赖驻留时间满足

|
(14) |
则存在切换状态反馈控制器:

|
(15) |
使得系统式 (6) 全局一致渐近稳定,且具有H∞性能上界:
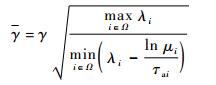
|
(16) |
证明 在切换状态反馈控制器u (t)=KσM(t)x (t) 的作用下,闭环链式平滑切换系统可写为
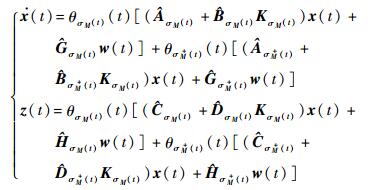
|
(17) |
1) 首先为系统选取Lyapunov函数为
Vi(x (t))=xT(t) Pi-1x (t) i∈ΩM
在链式切换律σM(t) 的作用下,设在t时刻第i个子系统被激活,即σM(t)=i,则有σM+(t)=i+或σM+(t)=i-,以下证明σM+(t)=i+的情况,可得
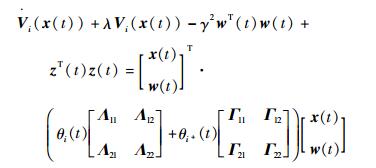
|
其中:

|
令

|
由Schur补引理易知,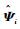

|
(18) |
式 (18) 可写为

|
其中:
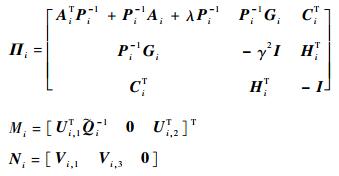
|


|
(19) |
由Schur补引理易知,式 (19) 等价为

|
(20) |
应用diag (Pi-1, I, I, I, I) 对式 (11) 做全等变换,则易知定理条件保证式 (21) 成立:
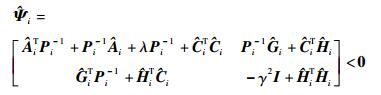
|
(21) |
同理可知

|
(22) |
综合式 (21) 和式 (22) 可知
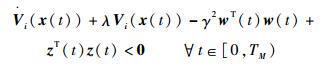
|
另外,由式 (12) 可知
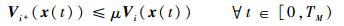
|
(23) |
不等式证毕。
为系统选取分段连续可微的Lyapunov函数V (x):Rn→R+,使得在第i个切换子系统被激活的时间内,有V (x)=Vi(x)。给定t>0,且t∈[tk, tk+1),其中tk为系统第k次切换的时刻,设此时第s个子系统被激活。
2) 证明切换系统的全局一致渐近稳定性
令w (t)≡0,在[tk, t) 内,有
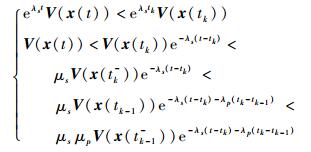
|
(24) |
式中:V (x (tk-)) 表示在tk时刻系统切换之前的Lyapunov函数,且在tk-1时刻第p个切换子系统被激活。令Nσi(0, t) 表示[0, t) 内第i个子系统被激活的次数,Ti(0, t) 表示[0, t) 内第i个子系统被激活的总时间,在[0, t) 内反复应用式 (24) 可得

|
(25) |
式中: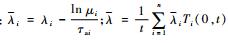
由平均驻留时间条件式τiM>τiM, *=ln μi/λi可知λi>0, ∀i∈Ω,又因为Ti(0, t)≥0, ∀i∈Ω,因此可得λ>0,从而连续自治切换系统是全局一致渐近稳定的。
3) 令ϕ(t)=zT(t) z (t)-γ2wT(t) w(t),类似稳定性的证明,在[tk, t) 内,有
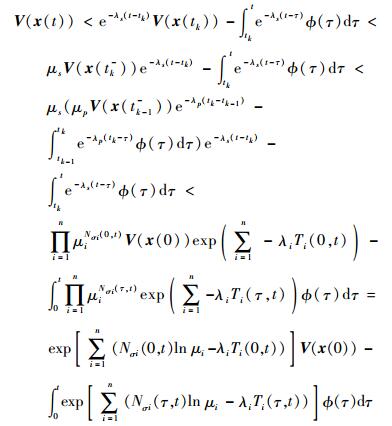
|
由零初始条件以及V (x (t))>0可得

|
(26) |
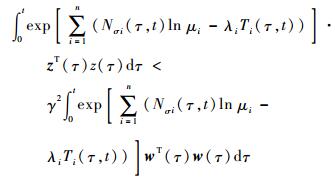
|
(27) |
又根据平均驻留时间条件式τiM>τiM, *=ln μi/λi可得
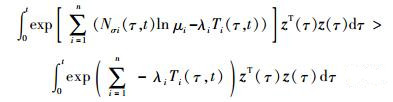
|
(28) |
且有

|
(29) |
综合式 (27)~式 (29),可得

|
(30) |
以[0, ∞) 为积分域对式 (30) 两端进行积分,其中左端可化为
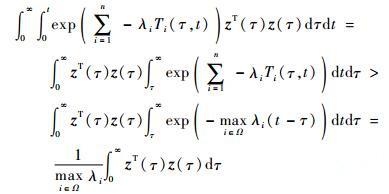
|
(31) |
右端可化为

|
(32) |
综合式 (30)~式 (32),得

|
(33) |
即切换系统式 (6) 具有H∞性能指标

|
推论1 考虑系统式 (6),如果对于∀i∈ΩM,以及给定的常数λi>0,μi>1,存在一组正定矩阵Pi>0,适维矩阵Ki和常数γ>0,εi>0,使得∀j, k∈{i, i+},下述线性矩阵不等式组成立:

|
(34) |
式中:
Mi, j, k=AjPi+PiAjT+λiPi+BjKkPi+PiKkTBjT
则设计如下的鲁棒平滑切换状态反馈镇定控制器:

|
(35) |
使得系统在满足式 (12) 和式 (13) 的条件时,有定理1的相同结论。记

|
式中:Li为适维矩阵,下面通过一类递推算法给出平滑切换控制增益的求解算法。
算法1 鲁棒平滑切换控制增益递推求解算法。
步骤1 取变体飞行器构型的链式切换初始指标为i=i0,针对给定的常数λi>0,μi>1,求解如下基于线性矩阵不等式组的优化问题:
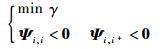
|
(36) |
解得矩阵Pi、Li和常数γ、εi,计算Ki=LiPi-1。
步骤2 对于已知的矩阵Pi和常数γ、εi,求解如下的线性矩阵不等式组:

|
(37) |
解得矩阵Ki+。
步骤3 对于已知的矩阵Ki+和常数γ,以及给定的常数λi+>0,μi, μi+>1,求解如下的线性矩阵不等式组:

|
(38) |
解得矩阵Pi+和常数εi+,令链式切换指标i=i+1,返回步骤2。
由上述步骤可知,算法1通过将原不等式条件Υi, j, k<0分解,给出递推求解平滑切换控制增益矩阵的方法,步骤1通过求解线性矩阵不等式组实现自启动,然后依据步骤2和步骤3的反复递推依次求解Ki+, Pi+, Ki+2, Pi+2, Ki+3, Pi+3, …。
3.2 跟踪控制与鲁棒H∞性能分析跟踪控制问题,即要求系统输出跟踪指令信号: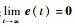

|
(39) |
针对变体飞行器的线性切换子系统模型,设计如下的切换跟踪控制器:
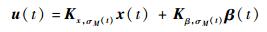
|
(40) |
同时,定义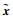
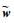

|
(41) |
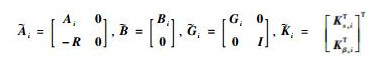

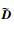
进一步考虑飞行动态的链式平滑切换特性,并将状态反馈切换控制相应地取为平滑切换控制律,如式 (42) 所示:
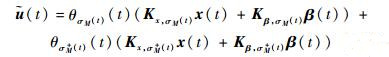
|
(42) |
在此基础上,将链式平滑闭环切换系统模型转化为广义切换系统形式,从而基于广义切换系统方法提出闭环系统的稳定性条件,分析系统的H∞性能,并进一步给出跟踪控制器的设计步骤。定义向量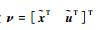
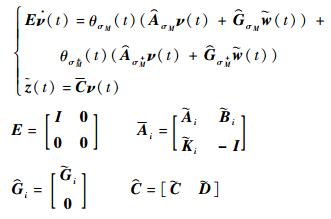
|
(43) |
通过上述增广转化,能够实现控制矩阵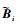
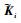
定理2 考虑变体飞行器广义链式平滑切换系统式 (43),令x (0)=0,如果对于∀i∈ΩM,∀ 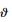

|
(44) |

|
(45) |

|
(46) |
式中:
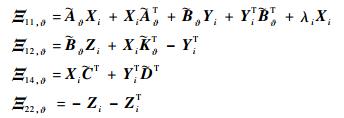
|
且系统在链式切换信号σM(t) 下的构型依赖驻留时间满足
τiM>τiM, *=(ln μi)/λi
则切换系统式 (43) 全局一致渐近稳定,且具有H∞性能上界
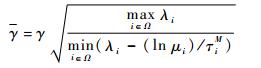
|
(47) |
证明 记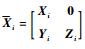
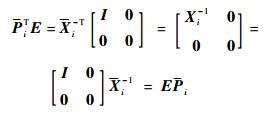
|
为系统选取分段连续可微的类Lyapunov函数V (x (t)):Rn→R+,使得在第i个切换子系统被激活的时间内,有

|
(48) |
根据式 (48) 再结合相关矩阵的定义可得
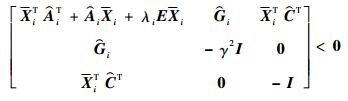
|
(49) |
用矩阵diag (Pi, I, I) 对不等式 (49) 做全等变换,则可得
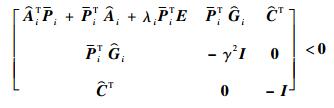
|
(50) |
则由Schur引理可知式 (50) 等价于
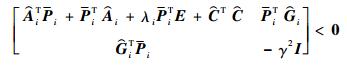
|
(51) |
同理可知
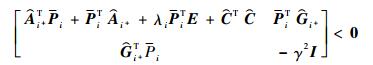
|
(52) |
故有
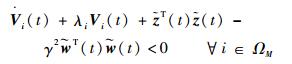
|
(53) |
又由式 (45) 和式 (46) 可知,对∀i∈ΩM,系统在链式切换信号σM(t) 下有如下不等式成立:

|
(54) |
证毕
由定理2可知,通过将广义平滑切换系统引入变体飞行器跟踪控制系统模型,实现了控制矩阵项
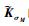


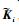
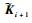
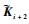
对于某一固定构型和一组给定的俯仰姿态,可以解算出对应的平衡点控制输入量δT和δe。这里选取迎角α=1°,俯仰姿态角θ=2°,对于变体飞行器的初始构型,可以解得稳态下的δT=0.63,δe=3.5°。选取线性系统状态量为x=[Δα Δq]T,控制量为u=[ΔδT Δδe]T。其中:Δα和Δq分别为迎角和俯仰角速率相对于平衡状态的偏差量;ΔδT和Δδe分别为油门开度和升降舵相对于平衡状态的偏差量。令干扰输入w (t)=e-0.1tsin (0.2πt)。高度h=12 000 m,马赫数Ma=0.5,引入各切换子系统的跟踪控制器,部分系统矩阵取值如下:

|
根据定理2的相关结论和递推算法,首先对初始构型i0=M15解算算法启动条件,这里采用极点配置法求解控制增益得到如下结果:
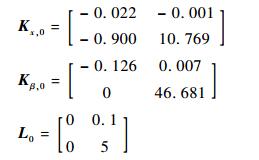
|
依次给定设计参数λi>0,μi>1,并按照递推算法可以依次求解得到其余的待求解矩阵,解得矩阵的具体数值这里不再全部列出,给出各子系统控制增益矩阵如表 2所示。
| 构型 | 反馈控制增益 | |
| Kx, i | Kβ, i | |
| M15 | 
|
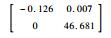
|
| M20 | 
|

|
| M25 | 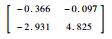
|

|
| M30 | 
|

|
| M35 | 
|

|
| M40 | 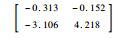
|

|
| M45 | 
|

|
| M50 | 
|

|
| M55 | 
|

|
| M60 | 
|

|
同时,可以计算相应子系统的构型依赖驻留时间条件和鲁棒H∞性能上界,需要说明的是变体飞行器在TM=20 s内经历10个构型,实际的构型依赖驻留时间τiM, i∈ΩM均可视为2 s,因此在给定设计参数λi和μi时,需考虑上述限制,并保证τiM, *=(ln μi)/λi<2, ∀i∈ΩM,则变体飞行器构型切换的驻留时间条件可以满足。
另外,经计算得到结果参数γ=0.835,利用鲁棒H∞性能上界公式 (47),计算得到γ=1.328。下面采用计算得到的控制增益结合跟踪控制器对变体飞行器变形飞行过程对应的闭环广义平滑切换系统进行仿真, 见图 1~图 5。

|
| 图 1 迎角响应曲线 Fig. 1 Angle of attack response curves |

|
| 图 2 俯仰角速率响应曲线 Fig. 2 Pitch angle rate response curves |

|
| 图 3 油门开度响应曲线 Fig. 3 Throttle position response curves |
|
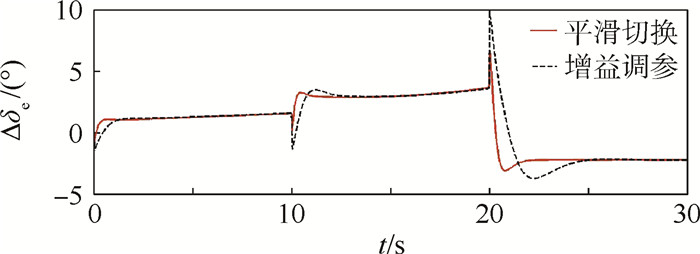
| 图 4 升降舵偏角响应曲线 Fig. 4 Elevator angle response curves |
|
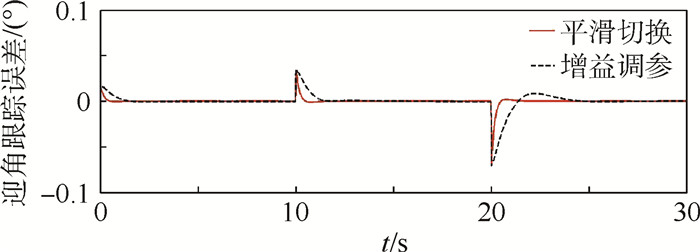
| 图 5 迎角跟踪误差曲线 Fig. 5 Angle of attack tracking error curves |
由仿真结果可以看出,所设计的跟踪控制器在变形过程中较好地实现了对迎角指令的跟踪,跟踪误差在可接受的范围内,对系统变形产生的扰动也具有良好的抑制效果。所设计的鲁棒平滑切换控制器实现了变形过程的平滑切换控制,系统状态响应未见明显的抖振,且控制效果略优于增益调参控制器的效果,从而表明本文所提鲁棒平滑切换控制方法的有效性。
5 结论本文考虑建立变体飞行器链式平滑切换系统模型,既能简洁、合理地反映变体飞行器的运动特性,又能兼顾其连续过渡的变形特征,且为降低设计的保守性提供了基础,主要结论有:
1) 针对变体飞行器在稳态飞行中快速变形的情况,基于构型依赖驻留时间方法分析具有链式切换律的平滑切换系统的全局渐近稳定性和鲁棒H∞性能。
2) 进一步设计了一种平滑切换镇定控制器的求解算法,将原有的硬切换方案转换为鲁棒平滑切换控制,并给出了一种基于LMI条件和递推算法的控制增益求解步骤。
3) 基于广义系统理论提出了保证变体飞行器姿态跟踪系统鲁棒稳定的充分条件,设计了广义系统鲁棒平滑切换跟踪控制器,从而确保变形过程中系统对姿态角指令的跟踪精度。
| [1] | WEISSHAAR T A. Morphing aircraft systems:Historical perspectives and future challenges[J]. Journal of Aircraft, 2013, 50 (2): 337–353. DOI:10.2514/1.C031456 |
| [2] | CROSSLEY W A, SKILLEN M D, FROMMER J B. Morphing aircraft sizing using design optimization[J]. Journal of Aircraft, 2011, 48 (2): 612–622. DOI:10.2514/1.C031180 |
| [3] | SOFLA A Y N, MEGUID S A, TAN K T, et al. Shape morphing of aircraft wing:Status and challenges[J]. Materials and Design, 2010, 31 (3): 1284–1292. DOI:10.1016/j.matdes.2009.09.011 |
| [4] | HUANG R, QIU Z P. Transient aeroelastic responses and flutter analysis of a variable-span wing during the morphing process[J]. Chinese Journal of Aeronautics, 2013, 26 (6): 1430–1438. DOI:10.1016/j.cja.2013.07.047 |
| [5] | POPOV A V, GRIGORIE L T, BOTEZ R. Closed-loop control validation of a morphing wing using wind tunnel tests[J]. Journal of Aircraft, 2010, 47 (4): 1309–1317. DOI:10.2514/1.47281 |
| [6] | BALDELL D H, LEE D H, PEÑR S S, et al. Modeling and control of an aeroelastic morphing vehicle[J]. Journal of Guidance, Control, and Dynamics, 2008, 31 (6): 1687–1699. DOI:10.2514/1.35445 |
| [7] | RUBAGOTTI M, ZACCARIAN L, BEMPORAD A. A Lyapunovmethod for stability analysis of piecewise-affine systems over non-invariant domains[J]. International Journal of Control, 2016, 89 (5): 950–959. DOI:10.1080/00207179.2015.1108456 |
| [8] | CHUMALEE S, WHIDBORNE J F. Gain-scheduled H∞ control via parameter-dependent Lyapunov functions[J]. International Journal of Systems Science, 2015, 46 (1): 125–138. DOI:10.1080/00207721.2013.775386 |
| [9] | ROMDLONY M Z, JAYAWARDHANA B. Stabilization with guaranteed safety using control Lyapunov-Barrier function[J]. Automatica, 2016, 66 : 39–47. DOI:10.1016/j.automatica.2015.12.011 |
| [10] | ANIMESH C, DANIEL T G, RICK L. Time-varying dynamics of a micro air vehicle with variable-sweep morphing[J]. Journal of Guidance, Control, and Dynamics, 2012, 35 (3): 890–903. DOI:10.2514/1.55078 |
| [11] |
乐挺, 王立新, 艾俊强. Z型翼变体飞机的纵向多体动力学特性[J].
航空学报, 2010, 31 (4): 679–686.
YUE T, WANG L X, AI J Q. Longitudinal multibody dynamic characteristics of Z-wing morphing aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31 (4): 679–686. (in Chinese) |
| [12] | YUE T, WANG L X, AI J Q. Longitudinal linear parameter varying modeling and simulation of morphing aircraft[J]. Journal of Aircraft, 2013, 50 (6): 1673–1681. DOI:10.2514/1.C031316 |
| [13] |
薛静, 杨亚洁, 刘宇, 等. 基于L1自适应控制的无人机横侧向控制[J].
西北工业大学学报, 2015, 33 (1): 40–44.
XUE J, YANG Y J, LIU Y, et al. Lateral roll angle control of UAV based on L1 adaptive control method[J]. Journal of Northwestern Polytechnical University, 2015, 33 (1): 40–44. (in Chinese) |
| [14] | SEIGLER T M, NEAL D A. Analysis of transition stability for morphing aircraft[J]. Journal of Guidance, Control, and Dynamics, 2009, 32 (6): 1947–1953. DOI:10.2514/1.44108 |
| [15] | CUI L, CHEN L, DUAN D P. Gain-scheduling model predictive control for unmanned airship with LPV system description[J]. Journal of Systems Engineering and Electronics, 2015, 26 (5): 1043–1051. DOI:10.1109/JSEE.2015.00113 |
| [16] | YUE T, WANG L X, AI J Q. Gain self-scheduled H∞ control for morphing aircraft in the wing transition process based on an LPV model[J]. Chinese Journal of Aeronautics, 2013, 26 (4): 909–917. DOI:10.1016/j.cja.2013.06.004 |
| [17] |
段广仁, 王好谦. 多模型切换控制及其在BTT导弹设计中的应用[J].
航空学报, 2005, 26 (2): 144–147.
DUAN G R, WANG H Q. Multi-model switching control and its application to BTT missile design[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26 (2): 144–147. (in Chinese) |
| [18] | HOU Y Z, WANG Q, DONG C Y. Gain scheduled control:Switched polytopic system approach[J]. Journal of Guidance, Control, and Dynamics, 2011, 34 (2): 623–629. DOI:10.2514/1.51699 |
| [19] | HOU Y Z, DONG C Y, WANG Q. Stability analysis of switched linear systems with locally overlapped switching law[J]. Journal of Guidance, Control, and Dynamics, 2010, 33 (2): 396–403. DOI:10.2514/1.45795 |



