计算机断层成像 (Computed Tomography,CT) 技术是指利用X射线穿透物体的衰减信息进行重建来获得物体断层图像的技术,该技术不但给医学诊断带来革命性的影响,还成功地应用于安检、工业无损检测等领域[1]。但在实际的应用过程中,由于受数据采集时间、辐射剂量等的约束,只能采集到不完全角度下的投影数据。不完全角度图像重建主要包含有限角度和稀疏角度2类问题,研究不完全角度CT图像重建问题,是降低CT扫描辐射剂量的有效手段,在实际应用中将会发挥较大的作用。
由Candes等[2]在2006年提出的压缩感知理论是一种在已知信号具有稀疏性或可压缩性的条件下,对信号数据进行采集、编解码的理论。在压缩感知理论的硬件实现方面,麻省理工学院成功研制出了MRI RF脉冲设备和编码孔径相机,Rice大学研制出了单像素相机和A/I转换器等。在X射线CT领域,基于迭代方法的压缩感知算法既能减少辐射剂量,又能保证图像质量[3]。
从优化的角度看,寻找最稀疏的信号表示本质上是一个l0最小化问题,而此问题是一个NP难问题,为此,研究者提出了诸多具有开创性的算法,这些算法基本上都可以归类为贪婪算法[4]、l1极小化和全变差 (Total Variation, TV) 最小化算法[5]。最近的研究表明,相对于贪婪算法和l1极小化算法,TV最小化算法在图像重建时可以更精确地保持图像的边缘细节,而这一点,在处理图像时是非常重要的。TV最小化算法的另一个优势在于,除了可以处理稀疏的信号和图像,还可以成功处理梯度稀疏的信号和图像。
近几年,诸多学者研究了CT图像重建的稀疏表示模型,取得了一些重要研究成果。普遍做法是先建立合适的目标函数,然后寻找求解目标函数的快速算法。Zhu等[6]在目标函数中加入小波变换,使得重建图像边缘更加清晰。邓露珍等[7]引入多尺度几何分析的Contourlet变换,提出一种基于Countourlet变换与分离Bregman相结合的算法。Nien和Fessler[8]将系统矩阵分为有序子集,然后采用增广Lagrangian方法对子集求解,提出有序-线性增广Lagrangian (OS-LALM) 算法。后来又提出了改进的松弛-OS-LALM算法[9]。Hao等[10]将先验信息加入到目标函数中,提出了基于低量CT图像的贝叶斯重建算法。这些算法有的能较好地恢复图像的整体信息,但存在小范围的伪影。有的重建出的图像没有明显的伪影,但是降低了重建效率。
为了平衡CT图像重建的质量与重建效率,本文提出更新图像增广Lagrangian (Update Image Augmented Lagrangian, UIAL) 算法。首先,提出了新的目标函数;其次,采用增广Lagrangian罚函数方法,将约束问题非约束化;再次,根据问题的性质,将目标函数分解为与之等价的3个子问题,通过在交替方向上更新迭代求解子问题,从而求得全局最优解;最后,通过计算机仿真实验,将所提出的算法应用于图像重建,并与其他算法进行对比,验证了本文算法用于CT图像重建时的质量和效率优势。
1 建立目标函数以解方程为主的迭代算法是一类重要的CT图像重建算法。假设待重建图像为u(x, y),把图像离散化为N=n×n的矩形区域,用单下标u1, u2, …,uN来从左到右、从上到下标记图像像素。设在所有角度下共有M条 (M<N) 射线穿过物体,每条射线穿过物体后得到一个投影值bj(j=1, 2, …, M)。根据射线衰减的物理性质,得到方程组:
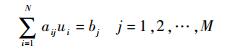
|
(1) |
式中:aij为射线j对像素ui的投影系数。用矩阵方程表示为
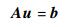
|
(2) |
式中:A为投影系数矩阵;b∈RM为图像u的投影向量。
可以看出,不完全角度CT图像重建问题实际上是大型稀疏欠定方程组的求解问题。因为有效方程的数量远小于未知数的个数,所以方程组有无数个解,需要找到一个最稀疏的解。这和压缩感知技术的思想本质上是一致的,由于全变差正则化不仅能够恢复稀疏信号或图像,而且能够成功地用于具有稀疏梯度的信号或图像,并且在保持边缘信息方面具有优势,所以可以用全变差正则化算法来描述不完全角度的CT图像重建问题:
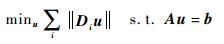
|
(3) |
式中:u∈RN;Diu∈R2为图像u的像素在i处的离散梯度;Α∈RM×N;║·║为1-范数或者2-范数。
为了更好地利用先验信息求解此优化问题,Chen等[11]利用代数重建 (ART) 算法和约束条件先求出先验图像,然后将重建出的先验图像加入到目标函数中,提出了先验约束压缩感知 (PICCS) 算法。其设定的目标函数为
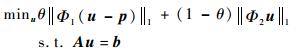
|
(4) |
式中:p为先验图像;Φ1和Φ2为任意稀疏变换;θ(0<θ<1) 为相对权重。Chen等[11]通过2个独立的步骤求解此约束最小化问题:第1步,根据Au=b使用ART算法得到先验图像p;第2步,将p作为已知量加入到目标函数中,使用最速下降法最小化目标函数。2步交替迭代,直至满足终止条件为止。
受其启发,针对不完全角度的CT图像重建问题,提出如下优化目标函数:
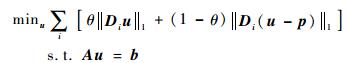
|
(5) |
不再通过ART算法单独求p,而是以上一步迭代得到的重建图像代之,不断更新目标函数。重建时将目标函数和约束条件一起考虑,采用罚函数中的增广Lagrangian方法[12]求解。
2 增广Lagrangian方法交替求解 2.1 增广Lagrangian函数对于等式约束问题:
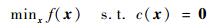
|
(6) |
式中:c为一个向量值函数;f和ci对于所有的i都是可微的。用增广Lagrangian方法将其变为无约束问题:
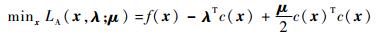
|
(7) |
式中:LA(x, λ; μ) 被称为增广Lagrangian函数。
可用迭代的方法解决增广Lagrangian函数最小化问题。假设第k次迭代估计为λk和μk>0,通过
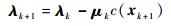
|
(8) |
来更新乘子[13]。
针对本文提出的模型式 (5),可以将之等价变形为
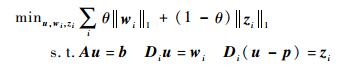
|
(9) |
该模型相应的增广Lagrangian函数为
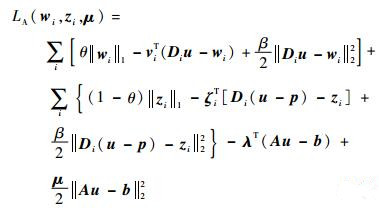
|
(10) |
由于式 (10) 仍然是凸优化问题,由全局收敛定理知,增广Lagrangian方法仍然能保证解的收敛性。设uk、wi, k、zi, k代表第k次迭代的最优解。通过
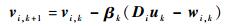
|
(11) |
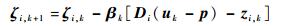
|
(12) |
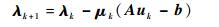
|
(13) |
来更新乘子。
求解时,将Lagrangian函数LA(wi, zi, μ) 的极小化问题转化为3个子问题,通过在交替方向上求解子问题[14],进而得到第k+1次迭代的最优解uk+1。
2.2 u-子问题在得到wi, k、zi, k、p之后,通过
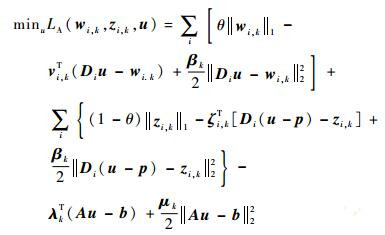
|
(14) |
来求解uk+1。此优化问题等价于u-子问题[15]:
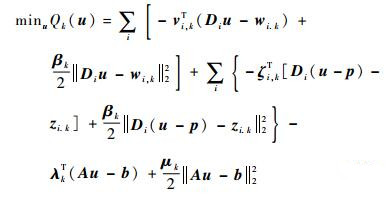
|
(15) |
易见,Qk(u) 是一个二次函数,可以利用最速下降法求解Qk(u) 最小化问题
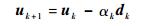
|
(16) |
式中:dk=dk(uk) 为Qk(u) 的梯度。
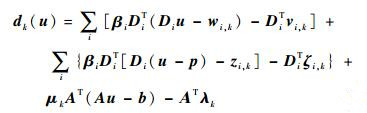
|
(17) |
由于wi, k、zi, k等参数是上一次迭代的最优解,不能保证全局最优,所以采用一步最速下降法来逼近Qk(u) 的最优解。
在迭代时,利用BB方法[16]来选择步长αk。根据式 (18) 或者式 (19) 计算出αk。
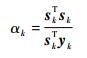
|
(18) |
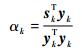
|
(19) |
式中:sk=uk-uk-1;yk=dk(uk)-dk(uk-1)。然后检验αk是否满足Armijo准则。如果αk不满足Armijo条件,则需要通过式 (20) 来减小步长0<ρ<1,直到满足条件为止。

|
(20) |
在得到uk+1、wi, k和zi, k之后,可以通过
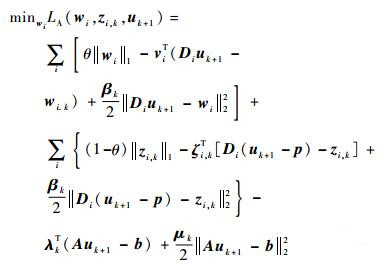
|
(21) |
来求解wi, k+1。此优化问题等价于w-子问题[15]:
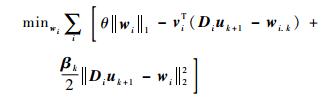
|
(22) |
由文献[13]知w-子问题的精确解为
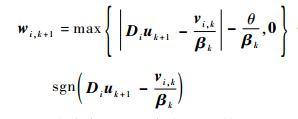
|
(23) |
为方便起见,将式 (23) 简记为
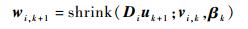
|
(24) |
在得到uk+1、wi, k+1和zi, k之后,可以通过
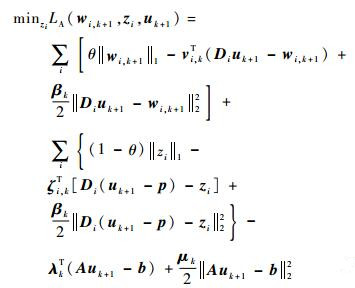
|
(25) |
来求解zi, k+1。此优化问题等价于z-子问题[15]:
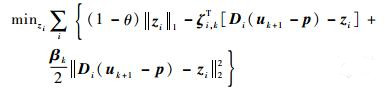
|
(26) |
由文献[13]知z-子问题的精确解为
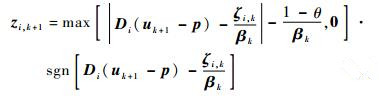
|
(27) |
为方便起见,将式 (27) 简记为
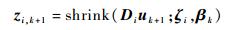
|
(28) |
由第2节的推导可以得到如下的更新图像增广Lagrangian算法框架:
初始化v0, ζ0, λ0, β0, μ0,0<θ, ρ<1,wi, 0, zi, 0, u0
While停止迭代条件不满足时Do
p=uk;
通过式 (18) 或式 (19) 计算步长αk;
While不满足Armijo条件时Do
αk=ραk;
End Do
通过式 (16) 一步最速下降法得到uk+1;
通过shrink式 (24) 计算wk+1;
通过shrink式 (28) 计算zk+1;
根据式 (11)~式 (13) 更新乘子;
End Do
4 仿真实验为了验证本文提出的UIAL算法在不完全角度图像重建问题中的性能,本文在有限角度和稀疏角度下对4幅医学图像进行重建,并比较了滤波反投影 (FBP) 算法、Split Bregman (SpBr) 算法与UIAL算法的重建结果。其中FBP算法是CT图像重建的经典算法,理论依据是“中心切片定理”,具有重建速度快的优点和对数据完备性要求高的缺点。Split Bregman算法由Goldstein和Qsher提出[17],是解决l1范数目标函数最小化的有效算法,已被广泛应用于图像处理的各个领域。相对于传统的算法,该算法能够较好地抑制由于数据不足带来的条状伪影,但是收敛速度较慢,重建时间较长。
测试计算机的配置为AMD A8(2.0 GHz),4GB内存,MATLAB2013编程平台。原始模型的像素为128×128,模拟平行光束扫描方式。将射线视为没有宽度的直线,投影系数值为射线贯穿每个像素的长度,采用Siddon[18]提出的交点排序法计算系统矩阵。经过多次试验,确定UIAL算法各参数的取值为:v0=0, ζ0=0, λ0=0, β0=20, μ0=28, θ=0.9,ρ=0.6, wi, 0=0, zi, 0=0, u0=ATb,迭代次数为1 000次。
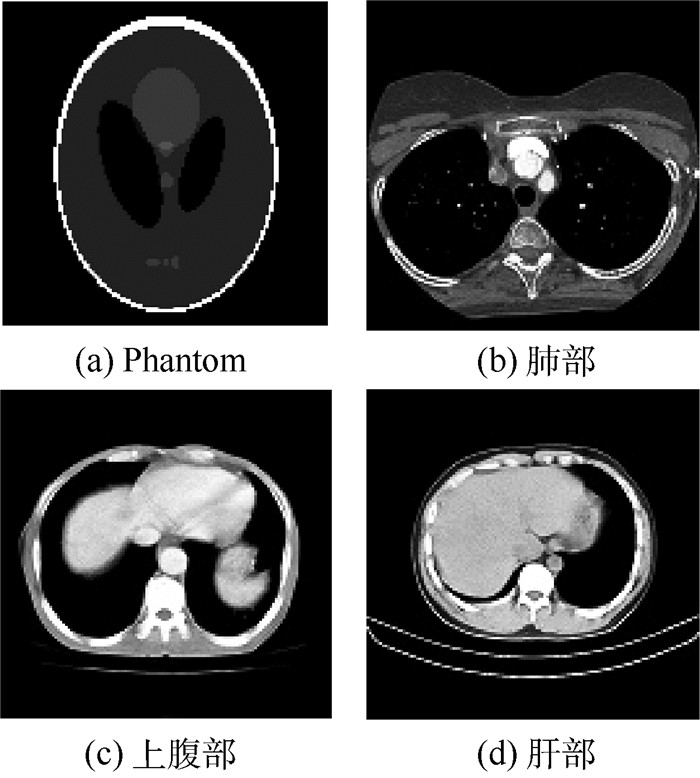
4幅用于测试的医学原始图像如图 1所示。
|
| 图 1 4幅医学的原始图像 Fig. 1 Four original medical images |
利用相对均方误差 (RRMSE) 和条纹指标 (SI) 来量化重建的效果[3],其中
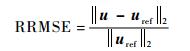
|
(29) |
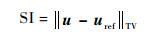
|
(30) |
式中:uref为原始图像。RRMSE和SI的值越小,表示重建效果越好。
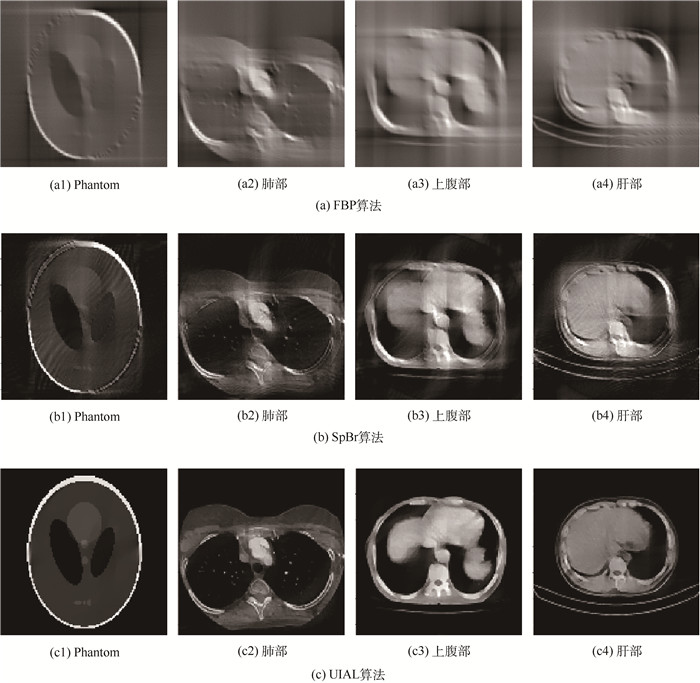
4.1 有限角度下的重建在有限角度问题中,测试限制在90°范围内采集投影数据。图 2为Phantom、肺部、上腹部和肝部的FBP、SpBr及UIAL 3种算法的重建图像。
|
| 图 2 有限角度下3种算法的重建图像 Fig. 2 Reconstruction images of three algorithms in limited view |
从图 2可以看出FBP算法重建的图像信息不完整,SpBr算法重建的图像有严重的伪影,而UIAL算法图像信息恢复完整且没有伪影。
同时利用RRSME和SI指标来量化比较重建结果,如表 1所示。
| 重建算法 | Phantom | 肺部 | 上腹部 | 肝部 | |||||||||||
| RRSME | SI | 重建时间/s | RRSME | SI | 重建时间/s | RRSME | SI | 重建时间/s | RRSME | SI | 重建时间/s | ||||
| FBP | 0.77 | 14.41 | 1.18 | 0.74 | 10.76 | 1.89 | 0.77 | 12.99 | 5.24 | 0.76 | 13.55 | 1.49 | |||
| SpBr | 0.48 | 10.41 | 155.28 | 0.41 | 8.13 | 149.06 | 0.41 | 9.90 | 202.54 | 0.37 | 10.69 | 201.22 | |||
| UIAL | 0.06 | 1.54 | 29.22 | 0.17 | 3.81 | 29.69 | 0.13 | 3.78 | 48.62 | 0.14 | 4.80 | 44.27 | |||
与FBP算法相比,UIAL算法耗费了较多的重建时间,但是相对均方误差分别下降了92.2%,77.0%,83.1%和81.6%,条纹指标分别下降了89.3%,64.6%,70.9%和64.6%,重建精度大幅度提高。与SpBr算法相比,UIAL算法的重建效率提高了4倍多,相对均方误差分别下降了87.5%,58.5%,68.3%和62.2%,条纹指标SI分别下降了85.2%,53.1%,61.8%和55.1%,重建效率和重建精度都有显著提升。
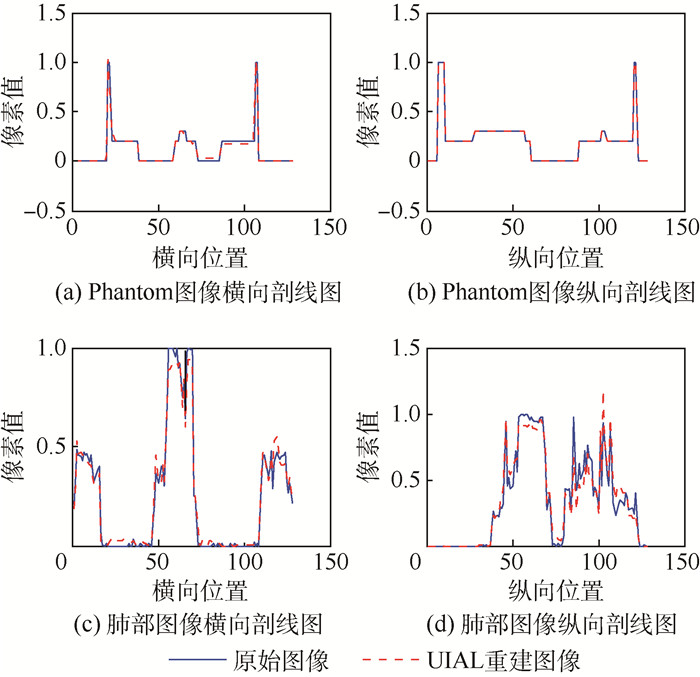
为了更精确地比较UIAL重建图像的像素值与原始图像的像素值之间差别,以前2幅图为例沿着图像在水平方向和垂直方向上的中心读取图像的像素值,并用横纵剖线图画出来,如图 3所示。
|
| 图 3 有限角度下重建图像与原始图像的像素比较 Fig. 3 Pixel comparison of reconstruction images with original images in limited view |
从图 3可以看出,UIAL算法重建出的图像与原始图像非常接近,具有很高的重建精度。
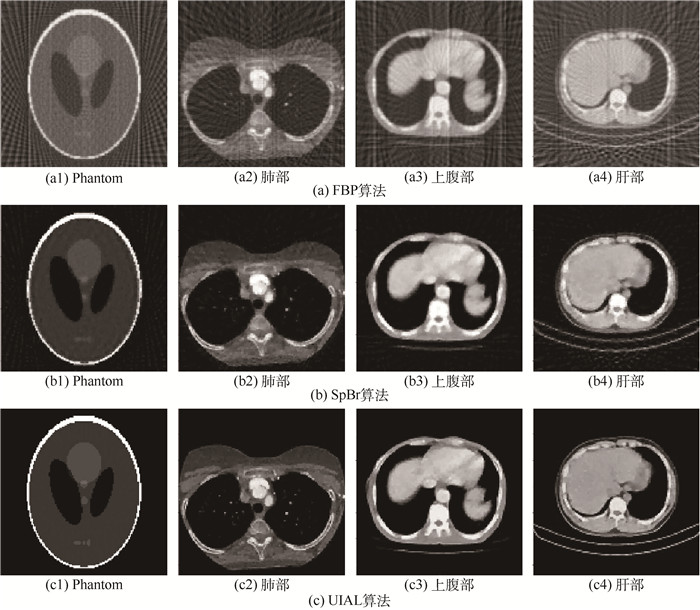
4.2 稀疏角度下的重建稀疏角度重建问题中,在180°范围内均匀采集40个角度的投影数据。图 4为Phantom、肺部、上腹部和肝部的FBP、SpBr及UIAL 3种算法的重建图像。
|
| 图 4 稀疏角度下3种算法的重建图像 Fig. 4 Reconstruction images of three algorithms in sparse view |
从图 4可以看出FBP算法重建的图像有严重的伪影,SpBr算法重建的图像细节模糊,而UIAL算法重建的图像没有伪影,细节清晰。
与FBP算法相比,UIAL算法耗费了较多的重建时间,但是相对均方误差分别下降了99.2%,60.7%,73.7%和73.1%,条纹指标分别下降了99.3%,61.1%,73.17%和74.62%,重建精度大幅度提高。与SpBr算法相比,UIAL算法的重建效率提高了许多,相对均方误差分别下降了98.5%,42.1%,50.0%和65.0%,条纹指标SI分别下降了98.5%,42.8%,53.2%和67.2%,重建效率和重建精度都有显著提升 (见表 2)。
| 重建算法 | Phantom | 肺部 | 上腹部 | 肝部 | |||||||||||
| RRSME | SI | 重建时间/s | RRSME | SI | 重建时间/s | RRSME | SI | 重建时间/s | RRSME | SI | 重建时间/s | ||||
| FBP | 0.38 | 12.13 | 1.19 | 0.28 | 9.47 | 1.29 | 0.19 | 8.87 | 1.52 | 0.26 | 12.49 | 1.73 | |||
| SpBr | 0.20 | 6.15 | 148.19 | 0.19 | 6.43 | 129.84 | 0.10 | 5.08 | 178.15 | 0.20 | 9.66 | 183.95 | |||
| UIAL | 0.003 | 0.09 | 23.60 | 0.11 | 3.68 | 24.06 | 0.05 | 2.38 | 28.02 | 0.07 | 3.17 | 17.49 | |||
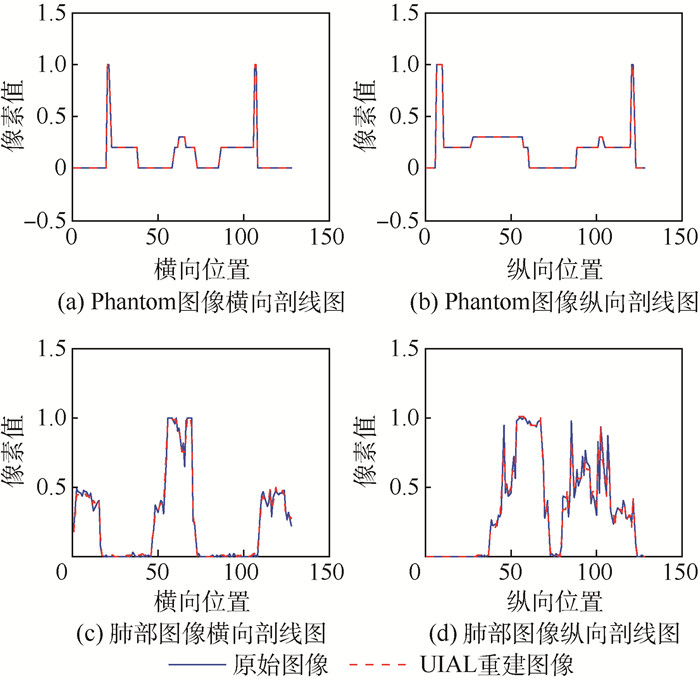
以前2幅图像为例,与原图像横纵剖线图 (见图 5) 比较可以看出,UIAL算法具有很高的精度。
|
| 图 5 稀疏角度下重建图像与原始图像的像素比较 Fig. 5 Pixel comparison of reconstruction images with original images in sparse view |
本文提出的稀疏表示模型相应的增广Lagrangian函数为
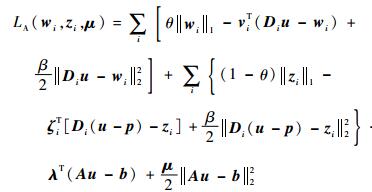
|
其主要参数为θ、v、β、ζ、λ和μ。
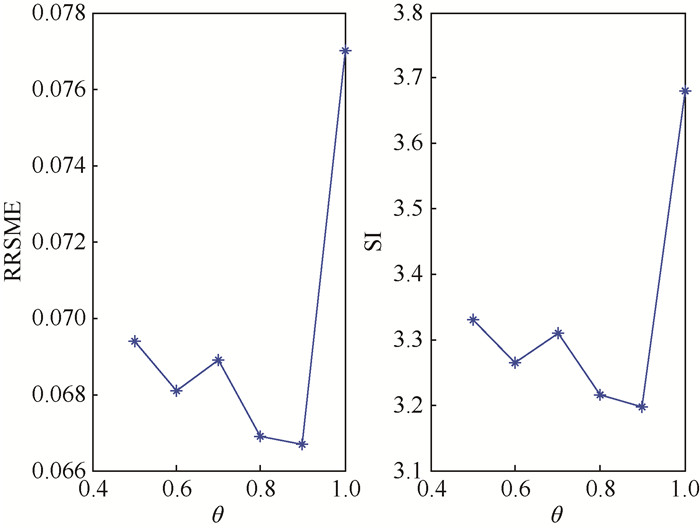
θ的选取:以肝部图像稀疏角度为例,当θ变化时,指标RRSME、SI的变化如图 6所示。
|
| 图 6 根据RRSME和SI的值找到最优的θ Fig. 6 Find optimum θ according to RRSME and SI |
当θ=0.9时,RRSME和SI的值最小,所以取θ=0.9。
v、β、ζ、λ和μ的选取是根据式 (11)~式 (13) 来更新计算。其中0<βk≤β, 0<μk≤μ,并且Hestenes[19]证明了该方法的收敛性。
5 结论本文提出了用于不完全角度CT图像重建的目标函数,并用增广Lagrangian方法求解,将算法称为更新图像增广Lagrangian (UIAL) 算法。通过仿真实验证明:
1) 在有限角度下重建,UIAL算法重建图像信息恢复完整且没有伪影。与SpBr算法相比,RRSME下降了58.5%~87.5%,SI下降了53.1%~85.2%,重建效率提高了4倍多。
2) 在稀疏角度下重建,UIAL算法重建图像没有伪影,细节清晰。与SpBr算法相比,RRSME下降了42.1%~98.5%,SI下降了42.8%~98.5%,重建效率提高了许多。
3) 重建图像与原图像的横纵剖线图比较,也可以看出UIAL算法具有很高的精度。
| [1] |
闫镔, 李磊.
CT图像重建算法[M]. 北京: 科学出版社, 2014: 97-112.
YAN B, LI L. CT image reconstruction algorithm[M]. Beijing: Science Press, 2014: 97-112. (in Chinese) |
| [2] | CANDES E, ROMBERG J, TAO T. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52 (2): 489–509. DOI:10.1109/TIT.2005.862083 |
| [3] | HASHEMI S, BEHESHTI S, GILL P R, et al. Accelerated compressed sensing based CT image reconstruction[J]. Computational & Mathematical Methods in Medicine, 2015 : 16797. |
| [4] | TROPP J A, WRIGHT S J. Computational methods for sparse solution of linear inverse problems[J]. Proceedings of the IEEE, 2010, 98 (6): 948–958. DOI:10.1109/JPROC.2010.2044010 |
| [5] | WANG Y, YANG J, YIN W, et al. A new alternating minimization algorithm for total variation image reconstruction[J]. SIAM Journal on Imaging Sciences, 2008, 1 (3): 248–272. DOI:10.1137/080724265 |
| [6] | ZHU Z, WAHID K, BABYN P, et al. Improved compressed sensing-based algorithm for sparse-view CT image reconstruction[J]. Computational & Mathematical Methods in Medicine, 2013 (18): 84–104. |
| [7] |
邓露珍, 冯鹏, 陈绵毅, 等. 一种基于Contourlet变换与分裂Bregman方法的CT图像重建算法[J].
CT理论与应用研究, 2014, 23 (5): 751–759.
DENG L Z, FENG P, CHEN M Y, et al. An CT image reconstruction algorithm based on Contourlet transform and Split Bregman methods[J]. CT Theory and Application Research, 2014, 23 (5): 751–759. (in Chinese) |
| [8] | NIEN H, FESSLER J A. Fast X-ray CT image reconstruction using a linearized augmented Lagrangian method with ordered subsets[J]. IEEE Transactions on Medical Imaging, 2014, 34 (2): 388–399. |
| [9] | NIEN H, FESSLER J. Relaxed linearized algorithms for faster X-Ray CT image reconstruction[J]. IEEE Transactions on Medical Imaging, 2016, 35 (4): 1090–1098. DOI:10.1109/TMI.2015.2508780 |
| [10] | ZHANG H, HAN H, LIANG Z R, et al. Extracting information from previous full-dose CT scan for knowledge-based Bayesian reconstruction of current low-dose CT images[J]. IEEE Transactions on Medical Imaging, 2016, 35 (6): 860–870. |
| [11] | CHEN G J, TANG J, LENG S. Prior image constrained compressed sensing (PICCS):A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets[J]. Medical Physics, 2008, 35 (2): 660–663. DOI:10.1118/1.2836423 |
| [12] |
袁亚湘.
非线性优化计算方法[M]. 北京: 科学出版社, 2008: 158-173.
YUAN Y X. Nonlinear optimization calculating method[M]. Beijing: Science Press, 2008: 158-173. (in Chinese) |
| [13] | LI C B.An efficient algorithm for total variation regularization with applications to the single pixel camera and compressed sensing[D].Houston, TX:Rice University, 2009:18-31. |
| [14] | XIE S L, GUAN C T, HUANG W M, et al.Fast TV MR image reconstruction using variable splitting and accelerated alternating direction method with adaptive restart[C]//2015 IEEE International Conference.Piscataway, NJ:IEEE Press, 2015:1085-1088. |
| [15] | PEACEMAN D W, RACHFORD H H. The numerical solution of parabolic and elliptic differential equations[J]. Journal of the Society for Industrial & Applied Mathematics, 2006, 3 (1): 28–41. |
| [16] | BARZILAI J, BORWEIN J M. Two-point step size gradient methods[J]. IMA Journal of Numerical Analysis, 1988, 8 (1): 141–148. DOI:10.1093/imanum/8.1.141 |
| [17] | GOLDSTEIN T, OSHER S. The split Bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2 (2): 323–343. DOI:10.1137/080725891 |
| [18] | SIDDON R L. Fast calculation of the exact radiological path for a three-dimensional CT array[J]. Medical Physics, 1985, 12 (2): 252–255. DOI:10.1118/1.595715 |
| [19] | HESTENES M R. Multiplier and gradient methods[J]. Journal of Optimization Theory & Applications, 1969, 4 (5): 303–320. |



