为了满足人类对于空间日益增加的应用需求,以及进一步提高空间系统的效益,以在轨组装、维护与补给等技术为标志的航天器近距离操控技术将成为未来航天技术发展的重要方向。而在任务的过程中,诸如测量、导航、控制等不可避免的误差因素都会导致航天器的实际轨迹偏离标称轨迹,极大地影响到任务的安全性。因此,有必要对近距离航天任务中的轨迹偏差进行分析和度量,以提高任务的安全性。
从传统可达问题扩展而来的相对可达区 (Relative Reachable Domain,RRD) 概念,可以用来描述航天器由于轨道初值的不确定性导致的轨迹偏差范围[1-2]。相对可达区的概念是由Wen等[3]首先提出的,是指初始状态不确定性导致航天器可能到达的位置集合,旨在用来分析入轨误差对集群飞行航天器轨道的影响。随后,Wen和Gurfil[4]采用参考点的方法对初值不确定情况下的平面相对可达区的计算方法进行了研究。石昊等[5]对上述方法进行了改进,将相对可达区的求解方法扩展到三维空间中,求解得到了航天器初值不确定性造成的轨迹偏差在空间中的包络曲面,并用Monte Carlo方法对结果的精度进行了验证。
在近距离操控任务中,为提高轨道控制精度,闭环控制方式是必不可少的,然而,上述研究只针对了航天器的自由飞行轨迹,闭环控制轨迹的相对可达区并未有涉及。在闭环控制系统中,轨道初值不确定性和控制、导航、测量等误差均会导致轨迹偏差,因此可将相对可达区的定义扩展为:相对坐标系下由于不确定性因素导致航天器可能到达的位置的集合。这样,相对可达区即是对相对运动轨迹偏差散布区域几何外形的描述。
对于闭环控制轨迹偏差问题,许多学者采用协方差分析方法进行了研究:Geller等[6-7]针对在轨闭环控制自主交会对接任务过程中的控制偏差和变轨时机问题进行了研究;李九人等[8]对仅测角导航条件下的闭环控制的相对导航协方差及相对运动轨迹控制协方差进行了分析;周洋等[9]对赤道大椭圆卫星在开环和闭环控制下的轨道机动精度进行了分析。但是,上述基于协方差理论的轨迹偏差分析法,并未能够对轨迹偏差散布区域的几何构型有一个完整的描述,因此存在着一定的不足。
本文将结合线性协方差分析法,采用相对可达区理论对闭环控制系统的航天器在近距离相对运动过程中的轨迹偏差散布区域进行研究。具体内容包括:①根据概率置信度定义航天器状态误差椭球,将时变的误差椭球集合而成为描述轨迹偏差的相对可达区;②采用协方差分析描述函数法 (CADET)[10]计算航天器状态的协方差矩阵;③给出采用协方差矩阵计算相对可达区的方法;④用Monte Carlo方法模拟真实轨迹,将求得的相对可达区包络与之进行对比,以验证方法的精度。
1 描述轨迹偏差的相对可达区首先定义相对运动的参考系,即LVLH (Local Vertical Local Horizontal) 参考坐标系:以航天器的质心为原点,地心指向航天器方向为x轴,轨道平面法向为z轴,y轴与x轴和z轴构成右手坐标系。
1.1 航天器状态误差椭球航天器实际状态的6维矢量可定义为
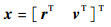
|
(1) |
式中:r和v分别为LVLH系中航天器的位置与速度矢量。由于存在测量、导航、控制等误差因素,x是一个随机矢量,其均值可表示为
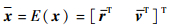
|
(2) |
式中:E(·) 为期望算子; x为航天器的标称状态矢量;r为标称位置矢量;v为标称速度矢量。定义状态误差矢量δx为
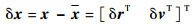
|
(3) |
假设δx服从高斯分布,则其概率密度函数为
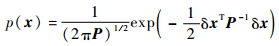
|
(4) |
式中:P为状态误差的6×6协方差矩阵,即
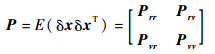
|
(5) |
式中:Prr、Prv、Pvr和Pvv均为P的3×3子矩阵。
6维状态误差分布的等概率密度面可表示为
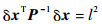
|
(6) |
式中:l为δx的马氏距离常数[11],其大小决定了等概率密度面的概率置信阈值。令A=P-1/l2,则式 (6) 可写为
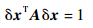
|
(7) |
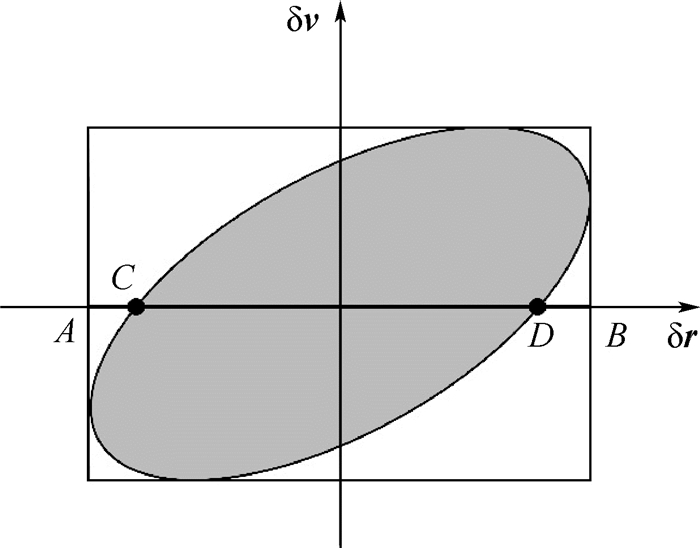
式 (7) 定义的6维超椭球面即为状态误差散布椭球的包络面。如以横轴表示6维状态误差空间的3维位置误差子空间δr,以纵轴表示3维速度误差子空间δv,则6维状态误差椭球即可表示在如图 1所示的平面内,图中阴影部分即表示6维状态误差椭球。
|
| 图 1 误差椭球 Fig. 1 Error ellipsoid |
由于对轨迹偏差的研究只关心表示位置误差的状态子空间,因此需要将表示位置误差的子矩阵从A中提取出来。现将6×6矩阵A划分为4个3×3子矩阵,即
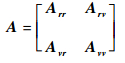
|
(8) |
则只有Arr是所需要的矩阵。有2种方法可以得到Arr:第1种方法是将6维协方差矩阵P求逆,除以l2得到A后直接将Arr提取出来;第2种方法是从P中提取出Prr,然后求逆并除以l2,即
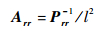
|
(9) |
从几何学角度上看,第1种方法是求6维椭球与3维位置子空间的相交部分,可表示为图 1中线段CD所示部分,而第2种方法则是将6维椭球在3维位置子空间上进行投影,即图 1中线段AB部分。显然,线段AB包含CD,这说明第2种方法更为保守。由于本文只关心位置子空间,在此采用第2种方法。
在3维位置空间内,航天器位于定义的误差椭球Arr内的概率可通过式 (10) 计算[12]:
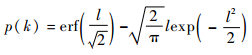
|
(10) |
式中:erf (·) 为高斯误差函数。当l=3时,航天器落在3维误差椭球内的概率为97.07%。
1.2 相对可达区的包络由第1.1节内容可知,航天器在t时刻的位置误差椭球可由函数F(r,t) 表示:
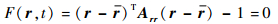
|
(11) |
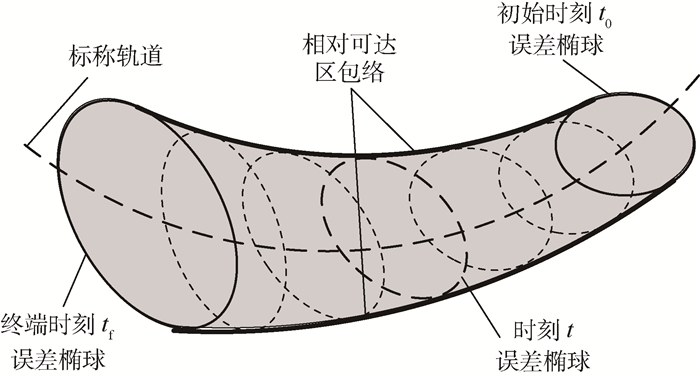
显然,相对可达区即为给定时间段内航天器位置误差椭球的集合。如图 2所示,虚线表示航天器的标称轨道,椭圆即为不同时刻的位置误差椭球,灰色区域为相对可达区。为了对相对可达区进行精确地描述,需要求出可达区的包络,即图 2中黑色粗实线所示的可达区边界。
|
| 图 2 相对可达区包络 Fig. 2 Envelope of RRD |
由文献[13]可知,式 (11) 定义了一簇随时间变化的椭球面,其包络面由这一簇椭球面及其所围区域的切曲面相交而成,可表示为
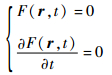
|
(12) |
式 (12) 的求解需要给出位置误差椭球矩阵Arr的值,而Arr依赖于位置误差协方差矩阵Prr,因此,求解相对可达区包络的首要问题就是求解航天器状态误差的协方差矩阵P。
2 闭环控制系统协方差分析由于计算简便,线性化的相对运动动力学方程被广泛地应用于航天器近距离相对运动的设计任务中,同时为简化问题起见,下文将以圆参考轨道为例,采用CW方程[14]描述航天器的运动。(注:此方法适用于任意参考轨道,方法带来的误差取决于动力学方程线性化的误差[6-7]。)
与开环系统相比,闭环控制系统在控制过程中增加了根据导航系统施加的轨道机动修正环节,本文假设修正方式为脉冲修正。因此,除了实际状态x和标称状态x外,还需定义航天器导航系统得到的估计状态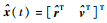
如采用扩展卡尔曼滤波 (EKF) 算法对系统状态进行估计,则闭环控制系统的控制过程可分为偏差预测、测量更新和控制修正3个基本过程[6-9]。为研究方便,现定义实际状态误差矢量δx=x,估计状态误差矢量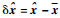
航天器实际的相对运动方程可写为
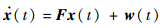
|
(13) |
式中:F为状态空间矩阵;w(t) 为零均值的高斯白噪声,表示未建模的系统随机扰动因素。过程噪声的协方差矩阵可表示为
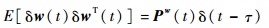
|
(14) |
式中:δ(t-τ) 为Dirac函数,且具有以下性质:
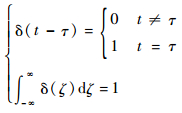
|
(15) |
在tk时刻,航天器实际状态的预测方程为
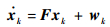
|
(16) |
式中:下标k表示tk时刻的状态量。
导航系统估计状态的预测方程为
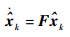
|
(17) |
对式 (16) 和式 (17) 在标称状态处进行线性化,可得实际误差和估计误差的预测方程:
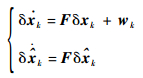
|
(18) |
受初始状态误差和控制系统的过程噪声等因素的影响,航天器状态误差的预测值和真实值会存在偏差,因此需要利用测量设备得到的测量信息对误差的预测值进行更新。
测量设备对航天器状态的观测方程可写为
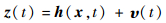
|
(19) |
式中:z(t) 为测量状态的显示值;h(x, t) 为测量状态的真实值;υ(t) 为测量误差。假设测量误差为零均值的高斯白噪声,则其协方差矩阵可写为Pυ(t)δ(t-τ)。
tk时刻的测量过程并不会改变航天器的实际状态,如用上标-m和+m分别代表航天器在测量更新前后的状态量,则有
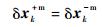
|
(20) |
式中:δxk-m为测量更新前的实际误差; δxk+m为测量更新后的实际误差。
但tk时刻的测量过程会更新导航系统的估计值,航天器估计状态的更新关系式可写为[12]
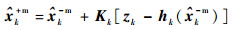
|
(21) |
式中:Kk为tk时刻的Kalman滤波增益矩阵[15]:
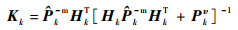
|
(22) |
式中:Hk为tk时刻的观测敏感矩阵:
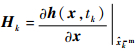
|
(23) |
将式 (21) 代入估计误差的定义式,并在标称状态处进行线性化,可得出估计误差测量更新过程的表达式
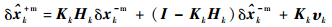
|
(24) |
式中:I为单位矩阵。
2.3 控制修正假设在tk时刻施加脉冲修正机动,分别用上标-c和+c表示航天器在脉冲修正机动施加前后的状态,则脉冲修正前后航天器实际状态的变化过程可表示为
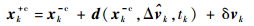
|
(25) |
式中:xk-c为修正前状态;xk+c为修正后状态;修正状态量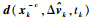
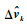
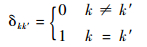
|
(26) |
将式 (25) 在标称状态处进行线性化,可得
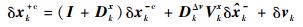
|
(27) |
式中:Dkx和DkΔv分别为修正状态量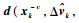
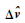
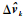
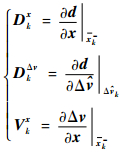
|
(28) |
导航状态在修正过程中同样会发生变化:
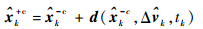
|
(29) |
将式 (28) 在标称状态处进行线性化,可得
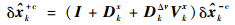
|
(30) |
由于要同时考虑实际误差和导航系统估计误差的变化,因此定义扩展误差矢量
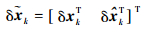
|
(31) |
由式 (18)、式 (20)、式 (24)、式 (27)、式 (30) 可得出扩展误差在tk时刻的预测、更新、修正关系式分别为
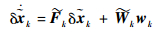
|
(32) |
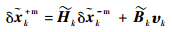
|
(33) |
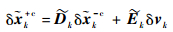
|
(34) |
式中:
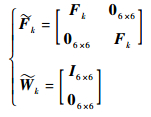
|
(35) |
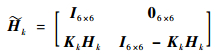
|
(36) |
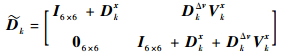
|
(37) |
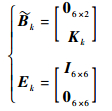
|
(38) |
根据协方差描述函数法,可得出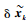
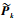
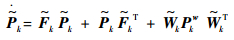
|
(39) |
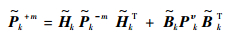
|
(40) |
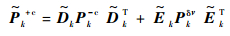
|
(41) |
式中:Pkw、Pkυ和Pkδv分别为tk时刻互不相关的控制系统随机噪声矩阵、测量噪声矩阵和控制偏差矩阵。
扩展协方差矩阵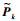
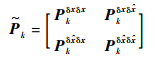
|
(42) |
求解相对可达区包络所需的航天器状态误差矩阵P即为所得扩展协方差矩阵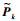
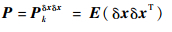
|
(43) |
求得航天器任意时刻的状态协方差矩阵P后,即对描述轨迹偏差的相对可达区的包络进行求解,将式 (12) 第2式展开,有
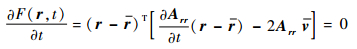
|
(44) |
式中:
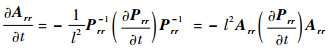
|
(45) |
式中: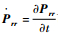
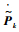
这样,可达包络的求解问题就转变为方程组 (12) 的求解问题,然而式 (12) 只能通过数值解法进行求解,初值和算法的选取将直接影响到结果的精度。因此,希望通过采用一定的手段,对表达式进行化简,提高求解的精度。
假设航天器的初始状态误差服从高斯分布,则初始协方差矩阵P0为实对称正定矩阵,此外,闭环控制系统的控制系统随机噪声、测量噪声和控制偏差也均假设服从高斯分布,由于可逆线性变换不改变实对称矩阵的正定性,因此,式 (39)~式 (41) 不会改变协方差矩阵P的正定性,即任意时刻的P都为实对称正定矩阵,显然Arr也为实对称正定矩阵。
根据有限维的谱定理,对于实对称正定矩阵Arr,存在实正交矩阵R,使得[16]
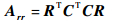
|
(46) |
式中:矩阵C和R取决于Arr的特征值和特征向量。假设λ1、λ2、λ3分别为实对称矩阵Arr的3个特征值,e1、e2、e3为相对应的特征向量,则矩阵C和R可写为
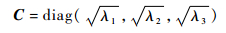
|
(47) |
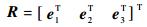
|
(48) |
将式 (46) 代入式 (11),可得
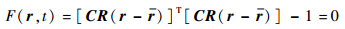
|
(49) |
定义矢量y1:
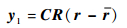
|
(50) |
则由式 (49) 可知,存在关系式:
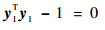
|
(51) |
式 (51) 表明,如果将矢量y1的起点固定,其终点将位于一个单位球面上。因此,通过式 (50) 的变换关系,可将式 (11) 所示的椭球面转变为一个单位球面。
利用式 (46) 和式 (50),可将式 (44) 写为
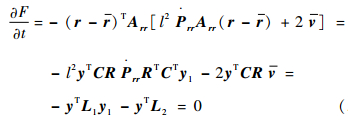
|
(52) |
式中:
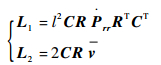
|
(53) |
这样,求解方程组 (12) 就等价于求解方程组
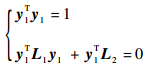
|
(54) |
此时,方程组的求解问题已经得到了一定程度的简化。如果将式 (54) 进行一定的坐标转换,将L2转变为只有一个分量为不为零的矢量,则还可进一步地简化求解过程。
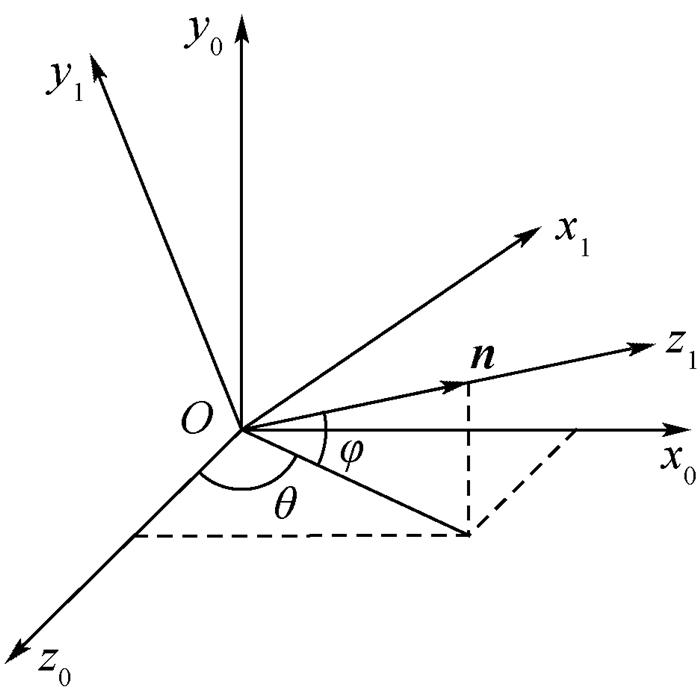
如图 3所示,定义坐标系S0(Ox0y0z0) 为式 (54) 中矢量L2所在的坐标系,坐标系S1(Ox1y1z1) 为目标坐标系,L2在坐标系S1中与z1轴重合,n为L2的单位方向矢量,θ、φ为矢量n在S1系中的方位角。则在S1系下求解方程组 (54) 时,会更为简便。
|
| 图 3 坐标系 Fig. 3 Coordinate systems |
S0系到S1系的坐标转换矩阵可写为
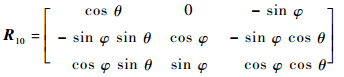
|
(55) |
令y2=R10y1表示y1在S1系中的投影,则
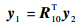
|
(56) |
而R10n=[001]T=ez,将式 (56) 代入式 (54) 得到
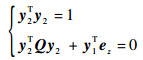
|
(57) |
式中:
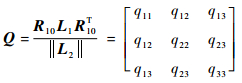
|
(58) |
显然,矢量y2的末端也位于一个单位球面上,假定α、β(0≤α, β≤2π) 为y2在S1系中的方位角,则矢量y2可表示为如下形式:
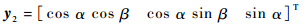
|
(59) |
将式 (59) 代入式 (57),可得
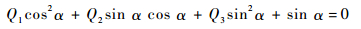
|
(60) |
式中:
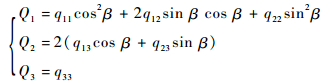
|
(61) |
任意给定α、β其中一个变量的值,利用牛顿迭代法求解式 (60) 即可得到另一个变量的值,将α、β代入式 (59) 中即可得到y2的值,对应的航天器位置矢量即可由式 (62) 求得
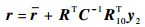
|
(62) |
遍历α或β的取值范围,即可求出相应的相对可达区的包络。
4 仿真算例对于圆参考轨道,式 (13) 中状态空间矩阵为
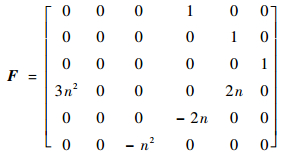
|
(63) |
式中:n为圆参考轨道的轨道角速度。
假设在tk时刻航天器施加机动修正脉冲,此时航天器的估计状态为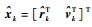
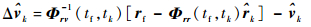
|
(64) |
式中:Φrr和Φrv为CW方程状态转移矩阵的子矩阵。由脉冲假设可知,控制过程中航天器的位置不会发生改变,因此有
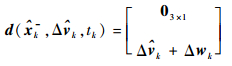
|
(65) |
则式 (28) 中各偏导数矩阵的表达式为
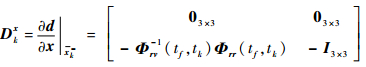
|
(66) |
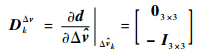
|
(67) |
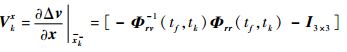
|
(68) |
主航天器位于半径R=7 000 km的圆轨道上,轨道周期T=5 800 s。t= 0 s时,一颗微小卫星被主航天器沿着LVLH系x轴方向释放入轨,释放速度大小为3 m/s。小卫星采用闭环控制系统进行控制。
则入轨时LVLH系下微小卫星的初始状态为
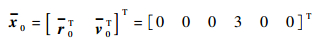
|
(69) |
由于存在测量、释放等误差,假定其初始状态偏差的协方差矩阵为
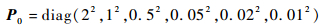
|
(70) |
其意义是在x方向位置偏差的标准差为2 m,y方向为1 m,z方向为0.5 m;x方向速度偏差的标准差均为0.05 m/s,y方向为0.02 m/s,z方向为0.01 m/s。注意,协方差矩阵并不一定是对角阵,这里只是取一个特例进行表示。
设小卫星导航系统误差协方差矩阵初值为

|
(71) |
采用中段修正法,即在0.5T(T为轨道周期) 时刻根据导航系统信息施加脉冲修正机动,使得小卫星在1T时回到标称轨道附近,控制系统的控制力误差大小为1%,方向任意。
在相对可达区包络的计算过程中,取马氏常数l=3,则实际轨迹位于包络中的概率为97.07%。算例将采用1 000次的Monte Carlo打靶法结果作为实际结果来与求得的包络进行对比,以验证方法的有效性。
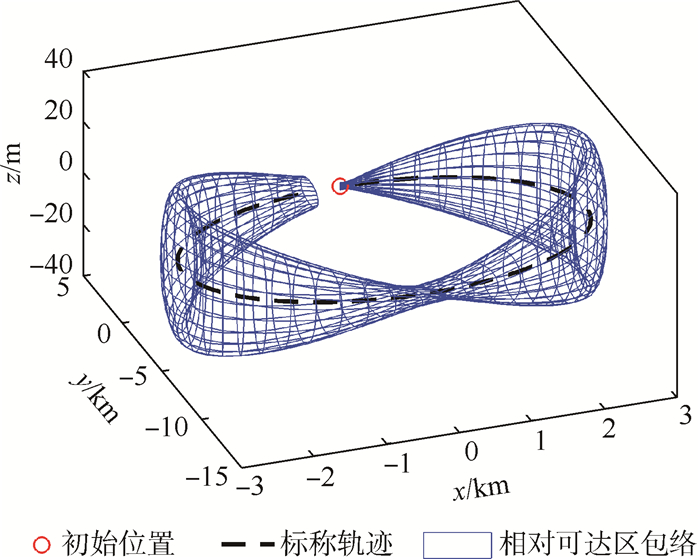
为了进行横向对比,首先计算开环控制系统下相对运动的轨迹偏差,即释放小卫星后不对其进行位置修正。如图 4所示为开环控制系统下的轨迹偏差仿真图,图中圆圈表示小卫星的初始位置,虚线代表其标称轨迹,网格线为开环控制时的相对可达区包络,其围成的区域即为相应的轨迹偏差散布区域。
|
| 图 4 开环系统相对可达区包络 Fig. 4 Envelope of RRD for open-loop system |
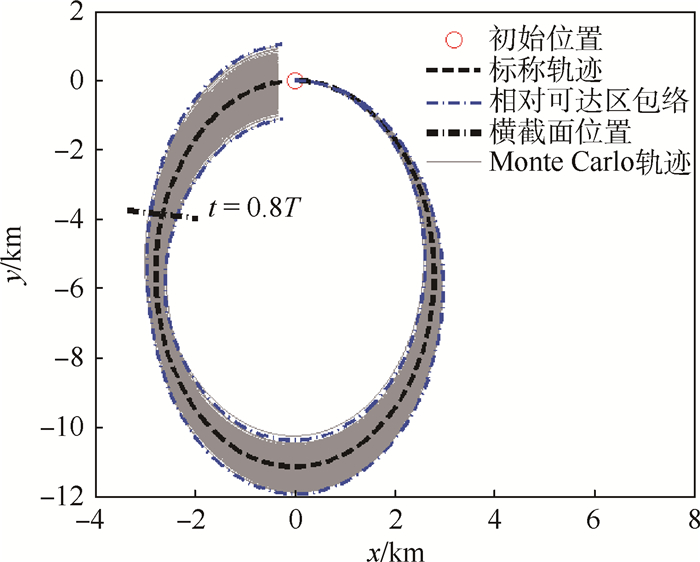
采用开环系统下的非线性相对运动动力学模型,随机取1 000个满足给定初始条件的初值,进行Monte Carlo仿真。实际轨迹的初值可通过MATLAB中的“mvnrnd”函数进行选取。将实际轨迹与求得的相对可达区包络在小卫星的标称轨迹面 (即x-y平面) 进行投影,得到图 5,图中标称轨迹用虚线表示,相对可达区包络的投影用细点画线表示,而Monte Carlo法得到的轨迹则用灰线表示,1 000条实际轨迹组成了一个灰色区域,可以认为是真实的轨迹偏差散布区域。从图 5中可以看出,绝大部分的灰色区域都位于相对可达区的包络之内,这是因为当马氏常数为3时,计算得到的包络包含真实轨迹的概率为97.07%,因此上述情况是合理的。
|
| 图 5 开环系统相对可达区包络与Monte Carlo轨迹的x-y平面比较 Fig. 5 Comparison of RRD envelope and Monte Carlo trajectories in x-y plane for open-loop system |
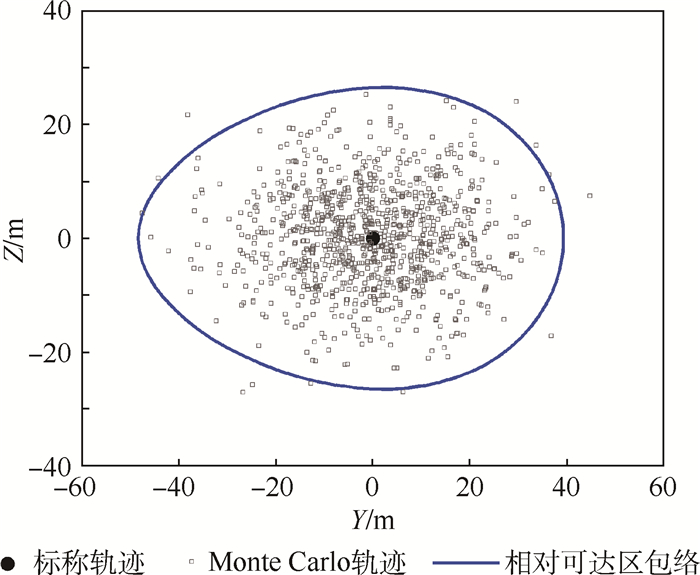
在t=0.8T时小卫星的标称位置处取垂直于标称轨迹的横截面,将相对可达区包络和Monte Carlo轨迹的比较结果在此平面上投影,如图 6所示。此横截面在标称轨迹上的位置在图 5中以点粗点画线标出。在上述截面建立截面坐标系XYZ,原点位于标称位置处,X向沿着此刻的标称速度方向,Z向垂直于标称轨迹所在的平面,Y轴构成右手坐标系。如图 6所示,绝大部分的小方块均位于可达包络之内,只有11个位于包络之外,概率为1.1%,小于给定概率2.93%。
|
| 图 6 开环系统相对可达区包络与Monte Carlo轨迹的横截面比较 Fig. 6 Comparison of RRD envelope and Monte Carlo trajectories in cross-section plane for open-loop system |
因此,对于开环系统的轨迹偏差散布区域的计算是符合真实情况的。
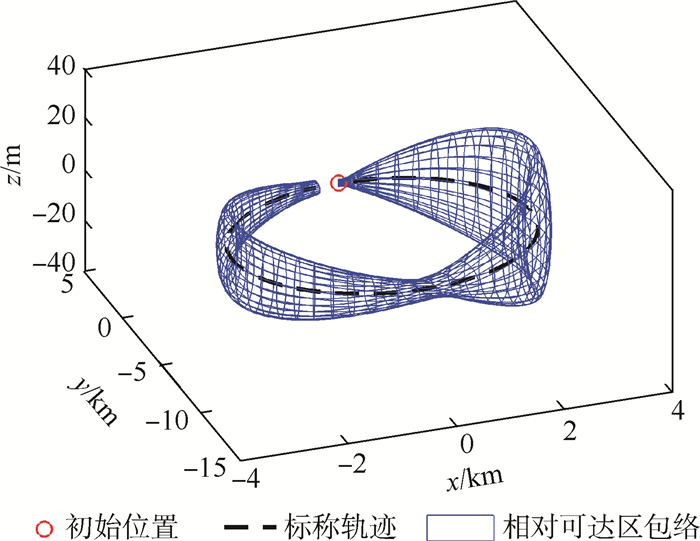
然后对闭环系统相对运动的轨迹偏差散布区域进行分析。图 7所示为闭环系统的相对可达区包络仿真图,与图 4比较可发现,闭环系统轨迹后半段的相对可达区包络在z向明显小于开环系统的包络,也就是说,在施加轨道修正机动后,z向航天器的轨迹偏差变小。
|
| 图 7 闭环系统相对可达区包络 Fig. 7 Envelope of RRD for closed-loop system |
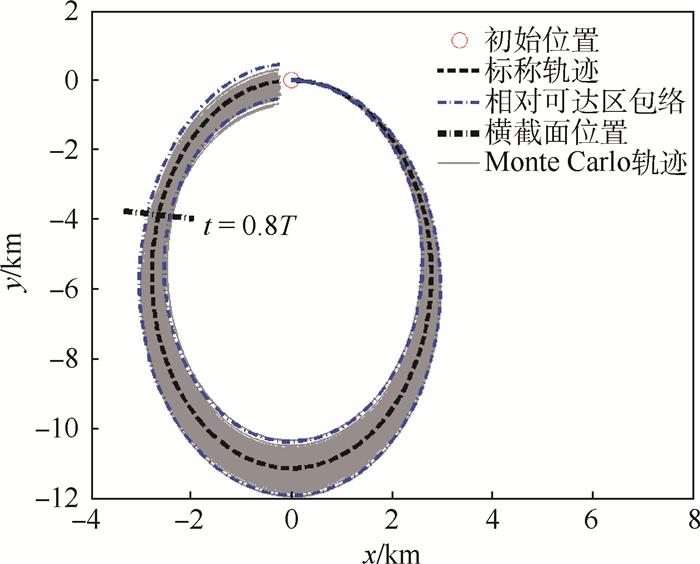
将闭环系统相对可达区包络与1 000次Monte Carlo仿真的比较结果在x-y平面内进投影,如图 8所示,可以发现,绝大部分的真实轨迹偏差散布区域都位于计算得到的相对可达区包络之内。将图 8与图 5进行比较后发现,施加修正脉冲后,x-y面内的轨迹偏差散布区域明显变小。
|
| 图 8 闭环系统相对可达区包络与Monte Carlo轨迹的x-y平面比较 Fig. 8 Comparison of RRD envelope and Monte Carlo trajectories in x-y plane for closed-loop system |
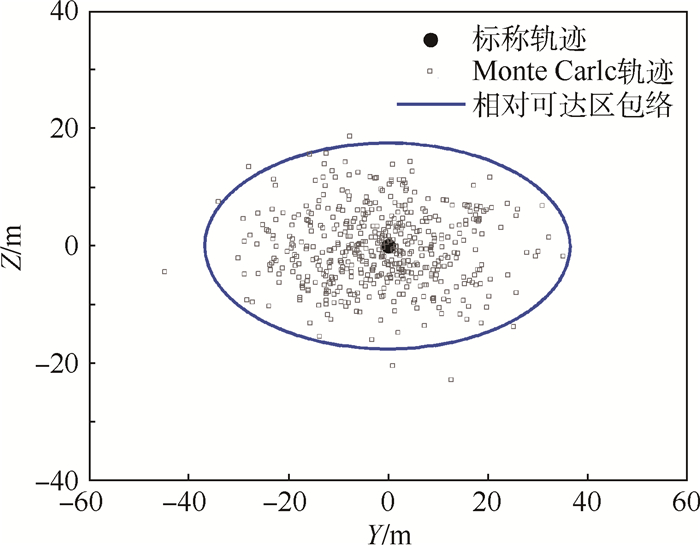
同样选取在t=0.8T时的横截面作为闭环系统下相对可达区与Monte Carlo结果的比较平面,如图 9所示,1 000次的Monte Carlo仿真中只有7次的结果位于相对可达区包络之外,概率为0.7%,小于给定值2.93%。将图 9与图 6进行对比,明显可以看出相对可达区的包络变小,这反映了闭环控制系统对轨迹的修正效果。
|
| 图 9 闭环系统相对可达区包络与Monte Carlo轨迹的横截面比较 Fig. 9 Comparison of RRD envelope and Monte Carlo trajectories in cross-section plane for closed-loop system |
因此,本文所述的方法可以切实有效地对闭环系统近距离相对运动地轨迹偏差进行分析。
5 结论本文以相对可达区理论为基础,结合协方差分析描述函数法推导了闭环控制系统下基于高斯分布的误差传递模型表达式,对航天器轨迹偏差的散布区域的几何构型进行了完整的描述,能够快速准确地计算描述给定概率阈值下航天器偏差分布区域,可用于分析航天器轨迹安全,并得到以下结论:
1) 本文所述方法能切实地反映闭环控制系统对轨迹的修正效果,可以有效地对航天器近距离相对运动中轨迹偏差散布的区域在几何上进行量化地描述。
2) 通过结合相对可达区理论与协方差分析描述函数法,航天器轨迹偏差散布区域的计算十分迅速,本文中相对可达区包络的计算时间仅需要1 s左右。
3) 通过仿真发现,航天器很小的速度误差都会导致很大的轨迹偏差,因此使用本文所述方法研究近距离相对运动的安全问题时不能忽略相对速度误差。
致谢
感谢中国科学院空间应用工程与技术中心的温昶煊对本文提供的技术支持。
| [1] | WEN C X, ZHAO Y S, SHI P. Precise determination of the reachable domain for a spacecraft with a single impulse[J]. Journal of Guidance, Control, and Dynamics, 2014, 37 (6): 1767–1779. DOI:10.2514/1.G000583 |
| [2] | WEN C X, ZHAO Y S, SHI P, et al. Orbital accessibility problem for spacecraft with a single impulse[J]. Journal of Guidance, Control, and Dynamics, 2014, 37 (4): 1260–1271. DOI:10.2514/1.62629 |
| [3] | WEN C X, ZHANG H, GURFIL P. Orbit injection considera-tions for cluster flight of nanosatellites[J]. Journal of Spacecraft and Rockets, 2015, 52 (1): 196–208. DOI:10.2514/1.A32964 |
| [4] | WEN C X, GURFIL P. Relative reachable domain for spacecraft with initial state uncertainties[J]. Journal of Guidance, Control, and Dynamics, 2015, 39 (3): 462–473. |
| [5] | 石昊, 赵育善, 师鹏, 等. 初值不确定轨道可达区域计算[J]. 宇航学报, 2016, 37 (4): 411–419. SHI H, ZHAO Y S, SHI P, et al. Determination of orbit reachable domain due to initial uncertainties[J]. Journal of Astronautics, 2016, 37 (4): 411–419. (in Chinese) |
| [6] | GELLER D K. Linear covariance techniques for orbital rendezvous analysis and autonomous onboard mission planning[J]. Journal of Guidance, Control, and Dynamics, 2006, 29 (6): 1404–1414. DOI:10.2514/1.19447 |
| [7] | GELLER D K, ROSE M B, WOFFINDEN D C. Event triggers in linear covariance analysis with applications to orbital rendezvous[J]. Journal of Guidance, Control, and Dynamics, 2009, 32 (1): 102–111. DOI:10.2514/1.36834 |
| [8] | 李九人, 李海阳, 唐国金. 仅测角导航的自主交会闭环控制偏差分析[J]. 宇航学报, 2012, 33 (6): 705–712. LI J R, LI H Y, TANG G J. Analysis of closed-loop control covariance for autonomous orbital rendezvous using angles-only relative navigation[J]. Journal of Astronautics, 2012, 33 (6): 705–712. (in Chinese) |
| [9] | 周洋, 闫野, 黄煦, 等. 航天器轨道机动的闭环控制精度分析[J]. 宇航学报, 2014, 35 (9): 1015–1021. ZHOU Y, YAN Y, HUANG X, et al. Accuracy analysis of closed-loop control for spacecraft orbit maneuver[J]. Journal of Astronautics, 2014, 35 (9): 1015–1021. (in Chinese) |
| [10] | GELB A, WARREN R S. Direct statistical analysis of nonlinear systems:CADET[J]. AIAA Journal, 1973, 11 (11): 689–694. |
| [11] | MAHALANOBIS P C.On the generalized distance in statistics[C]//Proceddings of the National Institute of Sciences.Calcutta:[s.n.], 1936, 2:49-55. |
| [12] | BRYSON A E, HO Y C. Applied optimal control:Optimization, estimation, and control[M]. Washington D.C.: Hemisphere Publishing Corporation, 1975: 309-311. |
| [13] | EISENHART L P. A treatise on the differential geometry of curves and surfaces[J]. Nature, 2004, 83 (83): 152–153. |
| [14] | CLOHESSY W H, WILTSHIRE R S. Terminal guidance system for satellite rendezvous[J]. Journal of the Aerospace Sciences, 1960, 27 (9): 653–658. DOI:10.2514/8.8704 |
| [15] | MAYBECK P S. Stochastic models, estimation, and control[M]. New York: Academic Press, 1974: 206-226. |
| [16] | BAPAT R B. Linear algebra and linear models[M]. 3rd ed.London: Springer, 2012: 23-25. |



