2. 华北电力大学 能源动力与机械工程学院, 北京 102206;
3. 北京科技大学 天津学院, 天津 301830
2. School of Energy, Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China ;
3. Tianjin College, University of Science and Technology Beijing, Tianjin 301830, China
夹层复合结构的设计理念和方法源于19世纪,最初为了寻求轻质但不失高强度、高刚度特性的板材。至今,轻量化的发展趋势使夹层板力学性能研究日趋成熟,包括蜂窝弹性变形、弹性屈曲、塑性坍塌和冲击性能[1-3]等诸多方面。针对蜂窝芯子,出现了包括多层级(hierarchical)蜂窝[4]、分层(graded)蜂窝[5]等新型结构形式,而正六边形蜂窝夹层板是目前较为基本且常见的一种夹层结构类型。在航空航天领域,为了使产品重量进一步减轻,出现了基于蜂窝夹层板进行预埋的设计方法,简单地讲,即将传统外部大型电器件改进为高度集成的电子模块埋入芯子内部。其最早由90年代洛克希德马丁航天公司在进行多功能结构设计中提出[6]。对于蜂窝夹层板而言,预埋设计即将蜂窝芯子进行局部挖空处理,将电子器件埋入挖空位置并进行保护加固设计。预埋结构是传统航空电子设备重量的10%~25%[7],使航天器设计在轻量化方面有了质的飞越。预埋设计的关键问题首先是对挖空后蜂窝芯材的强度评估,其次是后续如何设计预埋保护方案。而找出挖空导致的蜂窝芯子强度变化规律对于解决这2个关键问题具有重要意义。
蜂窝芯子挖空问题可以归结于蜂窝缺陷问题,属于蜂窝(壁)缺失这一缺陷类型。蜂窝缺陷一般由加工工艺所致,主要体现在其细观几何构型上,如波状蜂窝壁、非均匀壁厚、蜂窝壁缺失或断裂、蜂窝壁错位以及蜂窝(壁)缺失等[8]。Chen和Huang[9]用解析方法研究了波状蜂窝壁加非均匀壁厚双重缺陷下的整体力学性能;Chen等[10]通过有限元法研究了具有孔洞缺陷以及内含填充物的蜂窝力学性能;Chen和Huang[9]通过有限元法(FEM)研究了缺陷周围的应力集中分布规律,但仅限于单排单个的蜂窝壁;Ajdari等[11]研究了多种缺陷下常规蜂窝和非周期Voronoi蜂窝的整体力学性能,但缺少细节缺陷附近的细节分析。除正六边形蜂窝外,其他形式含缺陷的格子(lattice)型材料也得到了解析以及有限元形式的研究[12-15]。本文结合预埋特点,建立更具一般性和代表性的蜂窝(壁)缺失模型,采用有限元并结合解析方法对挖空部位应力集中分布规律展开研究。
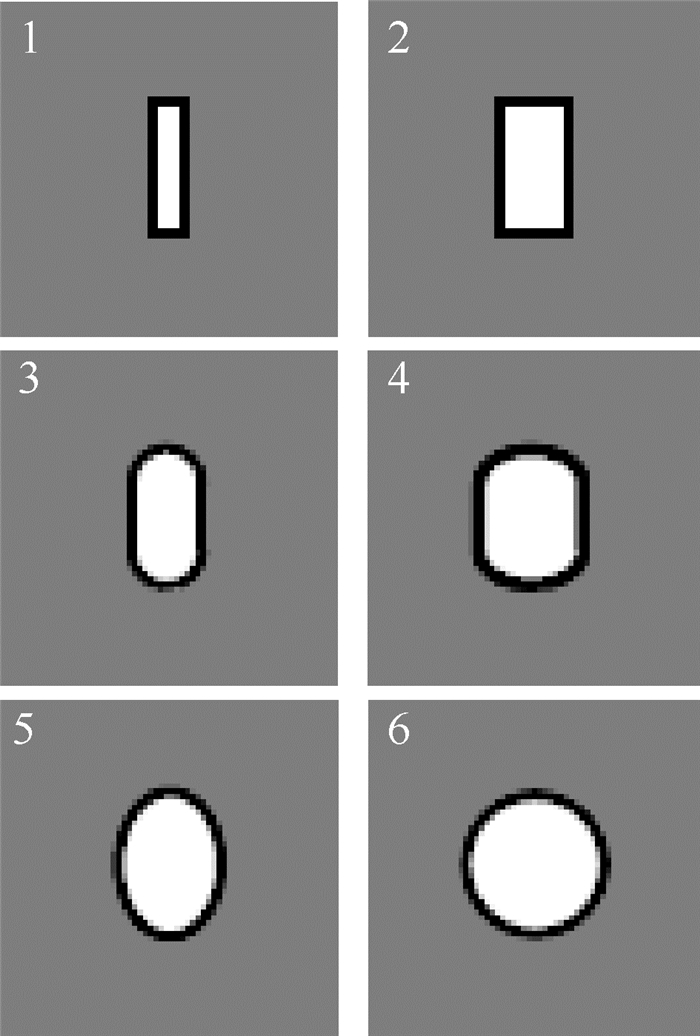
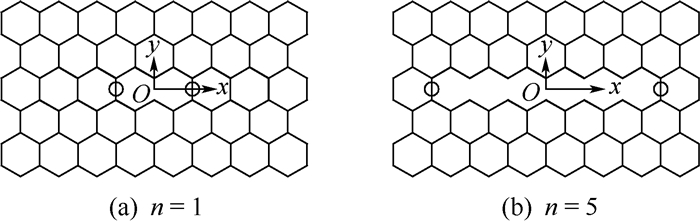
1 蜂窝壁缺失分类及模型建立研究蜂窝芯子挖空对整体强度的影响,首先要找到组成挖空部分的最小的周期性代表单元,Chen和Huang[9]取长度为h的竖向蜂窝壁作为最小单元,研究了缺陷孔周围的最大应力与单元缺失数量n的关系,如图 1所示分别为缺失1个单元(n=1)以及缺失5个单元(n=5)的结构示意图。但此种单元选择方式只局限于描述单排胞壁缺失形成的细长孔,而无法表达蜂窝壁大面积连续缺失形成的区域挖空。本文选取图 2所示的由5个蜂窝壁组成的叉树形单元(见图 3)来代替单个蜂窝壁,不同数量的叉树形单元的组合可以方便地描述不同大小和构型的挖空区域,很好地解决了上述问题。为了便于分析和描述,x为距离缺陷孔的水平距离,将x向缺失n个,y向缺失m个代表单元的情况记为mynx,如1y1x,1y5x和3y7x分别表示了m=1、n=1,m=1、n=5和m=3、n=7的单元缺失情况;另下文将图 1所示的缺失方式简记为第1类缺陷,而图 2为第2类缺陷。
|
| 图 1 蜂窝壁单个缺失 Fig. 1 Honeycomb with missing cell walls |
|
| σ2, maxP-缺陷蜂窝胞壁拉应力最大值;ycr-临界y值。 图 2 蜂窝壁单元缺失 Fig. 2 Honeycomb with missing cell wall elements |
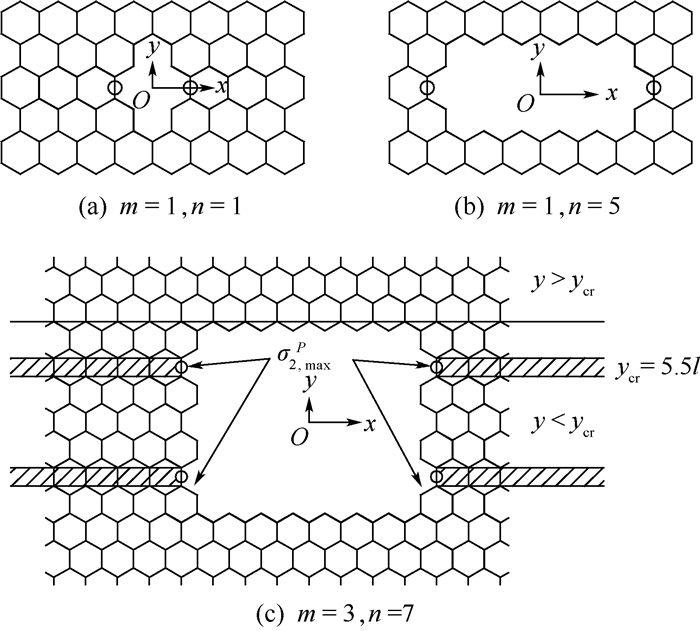
本文基于商业有限元软件ANSYS,采用APDL参数化设计语言构建含缺陷的蜂窝结构。具体方法见文献[16],本文采用2D模型进行分析。构建完毕的模型见图 3,蜂窝竖向壁长取h,斜向壁长取l,斜向臂倾角取θ,本文针对正六边形蜂窝,即θ=30°,同时有l=h,蜂窝宽度取w,蜂窝高度(垂直于x向和y向)取单位1,厚度为t。每个蜂窝壁离散为4个二阶Timoshenko梁单元。施加如图 3所示的边界条件,其中芯子一端取一个节点进行铰支约束,同侧其余节点滚动支持;另一端施加y向等值拉力P2∞=σ2∞t,σ2∞为完整蜂窝胞壁拉应力。
|
| 图 3 缺陷蜂窝芯子有限元模型及缺失单元 Fig. 3 Finite element model of honeycomb core with defects and corresponding missing element |
完整蜂窝在二向均匀拉伸条件下,蜂窝壁沿y向产生均匀拉应力σ2∞;而产生缺陷后,在离缺陷最近的蜂窝壁A上除拉力(记P2def)增加外,弯矩(记M2def)同样增大。蜂窝壁截面应力σ2def由两部分构成:一部分是由P2def产生的拉应力记σ2P,另一部分是由M2def产生的弯曲应力记为σ2M。本文对于σ2P的计算采用有限元法,而对于σ2M的计算则采用材料力学的解析方法。
2 缺陷处拉应力带状分布规律针对第1类缺陷,即单个长度为h的蜂窝壁连续缺失的情形,Gibson和Ashby[1]以缺失数量为参数,给出了缺陷蜂窝的σ2P与完整蜂窝的σ2∞之间的函数关系(式(1)),并得到Chen和Ozaki[8]的修正(式(2))。
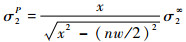
|
(1) |
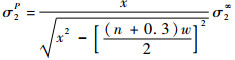
|
(2) |
式(1)和式(2)可用以计算图 1所示第1类缺陷孔端部周围的蜂窝胞壁应力值,但其对本文所提出的第2类缺陷并不适用。
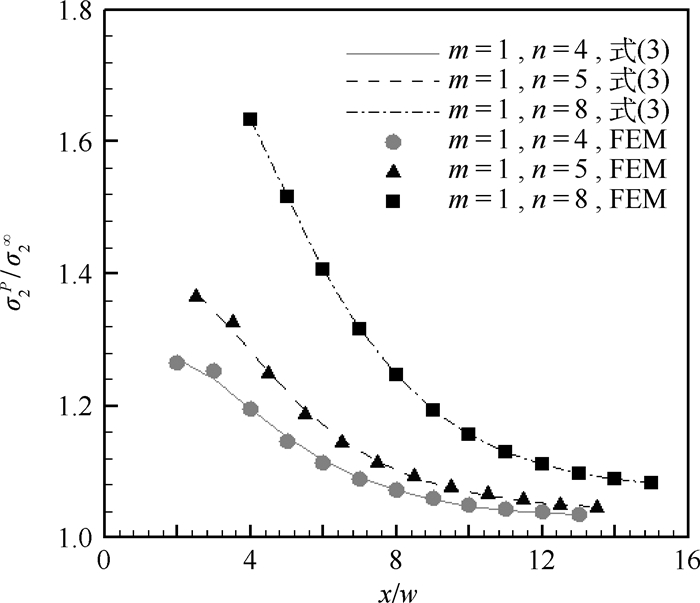
有限元计算获得的胞壁应力值沿x=0呈对称分布,因此本文只讨论x>0的情况。对于第2类缺陷类型,分别以m=1,n=4, 5, 8为例,给出了应力集中带,即y=1.5l,x=3w, 4w, …, 15w的带状区的胞壁标准化拉应力的有限元计算结果,如表 1所示,其中,标准化方法是用完整蜂窝的胞壁拉应力σ2∞去除上述缺陷条件下得出的有限元结果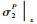
| x/w | σ2P/σ2∞ | ||
| n=4 | n=5 | n=8 | |
| 2(2.5) | 1.265 7 | (1.365 1) | |
| 3(3.5) | 1.252 9 | (1.325 9) | |
| 4(4.5) | 1.195 1 | (1.249 2) | 1.628 5 |
| 5(5.5) | 1.146 7 | (1.188 0) | 1.528 0 |
| 6(6.5) | 1.112 3 | (1.144 5) | 1.403 9 |
| 7(7.5) | 1.088 3 | (1.114 1) | 1.308 9 |
| 8(8.5) | 1.071 5 | (1.092 7) | 1.241 4 |
| 9(9.5) | 1.059 4 | (1.077 1) | 1.193 5 |
| 10(10.5) | 1.050 5 | (1.065 6) | 1.158 9 |
| 11(11.5) | 1.043 9 | (1.056 9) | 1.133 3 |
| 12(12.5) | 1.038 9 | (1.050 1) | 1.114 0 |
| 13(13.5) | 1.034 9 | (1.044 8) | 1.099 0 |
| 14 | 1.087 2 | ||
| 15 | 1.077 8 | ||
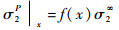
|
(3) |
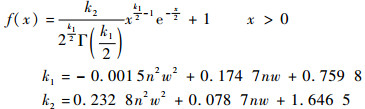
|
(4) |
式中: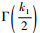
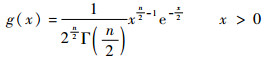
|
(5) |
本文将缺陷条件下的胞壁拉应力有限元结果标准化后(见表 1)绘于图 4中, 同等缺陷条件下的解析值和有限元值符合良好。另外,将另外2种函数形式(式(6)和式(7))的拟合精度分别在表 2中给出。其中,式(6)为指数型通用拟合函数;式(7)则是根据式(2)推导得来的通用拟合函数。相对误差见表 2所示。结果表明,用式(3)可以较为准确地预估缺陷应力分布,而用表达第1类缺陷应力分布的式(2)则会产生较大误差。
|
| 图 4 应力集中带状区胞壁标准化拉应力分布 Fig. 4 Normalized tensile stress distribution of cell walls in stress concentration strip area |
| % | |||
| 公式号 | n=4 | n=5 | n=8 |
| 式(3) | 0.04 | 0.07 | 0.19 |
| 式(6) | 0.40 | 0.66 | 1.80 |
| 式(7) | 1.98 | 16.10 | |
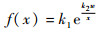
|
(6) |
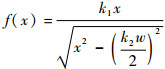
|
(7) |
通过有限元计算结果,本文发现第2类缺失的蜂窝壁组合与应力分布有如下关系:
在y=±(m-1)/2×3l的带状区(见图 2中的阴影区域)上的壁内拉应力值明显高于周围蜂窝壁,最大应力值σ2, maxP出现在带状区内离缺陷孔最近的蜂窝壁上,例如图 2中所圈注的蜂窝壁。
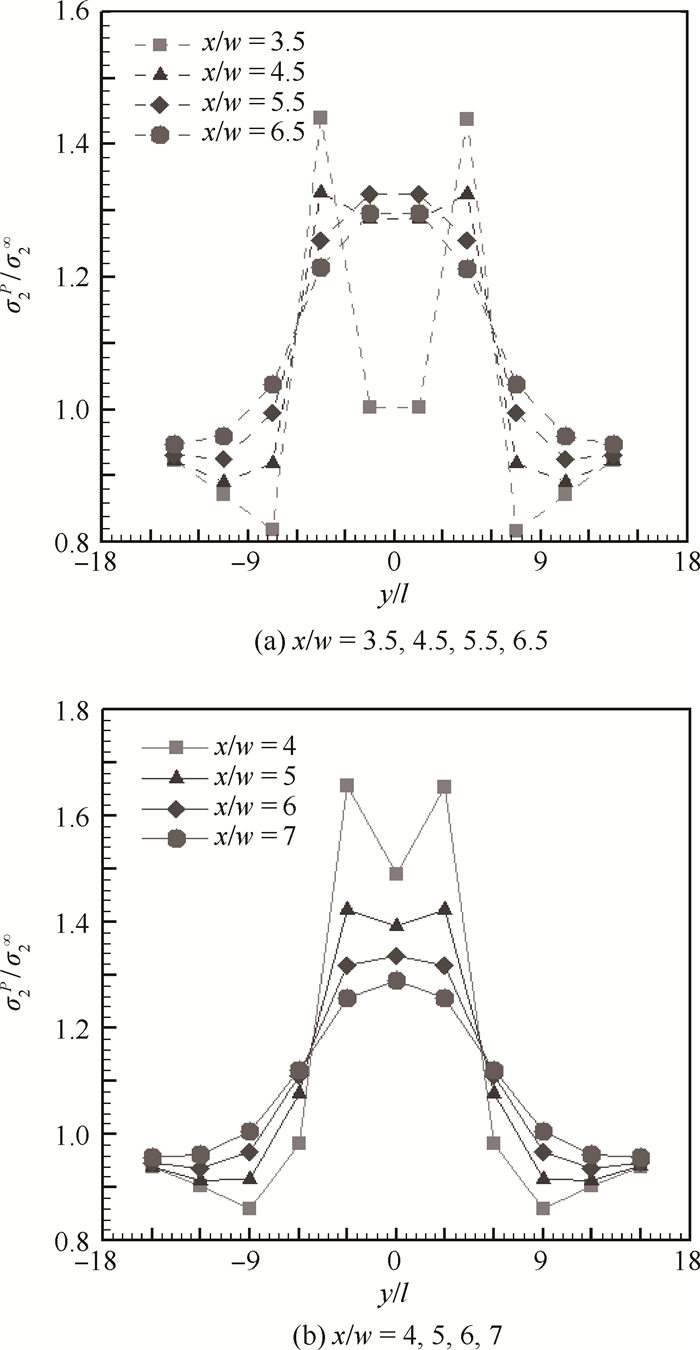
为了验证以上结论,此处采用图 5加以说明。取图 2中m=3,n=7的缺陷条件为例,在图 5中给出了从x=3.5到x=7的竖向蜂窝壁内拉应力分布。可以看出,拉应力值以y=0呈对称分布。最大应力出现在y=±3l位置处,符合本节第1种结论。
|
| 图 5 m=3, n=7缺陷附近竖向蜂窝壁内拉应力分布 Fig. 5 Tensile stress distribution of y-direction honeycomb walls with defect of m=3, n=7 |
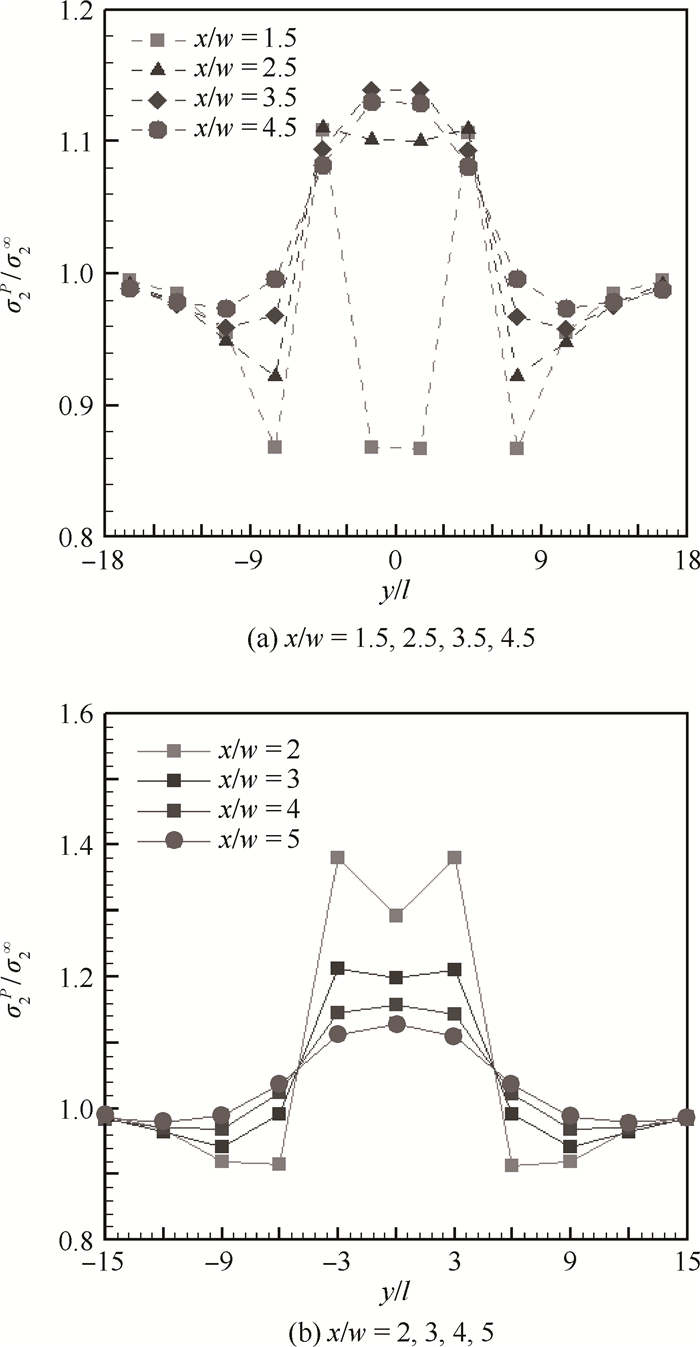
图 5~图 7所示为不同缺失单元条件下各x处的蜂窝壁拉应力y向分布。为便于比较,图中按x/w是否为整数分为2类并分别绘出。当m=3, n=7时,比较图 5(a)和图 5(b),给定x值,除包围缺陷孔的第1层(x/w=3.5)和第2层(x/w=4.5)蜂窝壁外,壁内拉应力随|y|的增大逐渐递减,并在无限远处趋于稳定值σ2∞;第1和第2层在y向靠近孔中心的位置(即y/l=0附近)为低应力区。但随着y值的增大,拉应力随x增加呈先增后减的趋势。存在一个临界y值(ycr),使得在y < ycr时,x越大(x方向距离缺陷孔中心越近),应力值越大,最小值出现在y/l=1.5处;而y > ycr时,x越大,应力值反而越小,在无限远处趋于稳定值σ2∞。其中,ycr为图 5(a)和图 5(b)所示的4条线的交点横坐标,且ycr∈[5l, 5.5l],从图 2可以看出,此范围之内不存在y向蜂窝壁。又因同一蜂窝壁的拉应力值相同,故本文以单个蜂窝壁为计数单位,因而ycr可取[5l, 5.5l]中的任意数值,此处取ycr=5.5l。另外,y/l=5.5处即为缺陷孔的上边界,若沿孔的上边界画一条线,此线是使应力分布出现上述分化的一个临界线。
|
| 图 6 m=3, n=3缺陷附近竖向蜂窝壁内拉应力分布 Fig. 6 Tensile stress distribution of y-direction honeycomb walls with defect of m=3, n=3 |
|
| 图 7 m=5, n=1缺陷附近竖向蜂窝壁内拉应力分布 Fig. 7 Tensile stress distribution of y-directionhoneycomb walls with defect of m=5, n=1 |
图 6所示为m=n=3条件下的应力分布,同m=3,n=7的结论类似。给定x值,除包围缺陷孔的第1、第3层(x/w=1.5, 2.5)和第2、第4层(x/w=2,3)蜂窝壁外,壁内拉应力随|y|的增大逐渐递减,并在无限远处趋于稳定值σ2∞;第1、第2层在y向靠近孔中心的位置(即y/l=0附近)应力较低。随着y值的增大,拉应力随x增加先增后减,出现拐点的位置在y=ycr∈[5l, 5.5l],在无限远处趋于稳定值σ2∞。
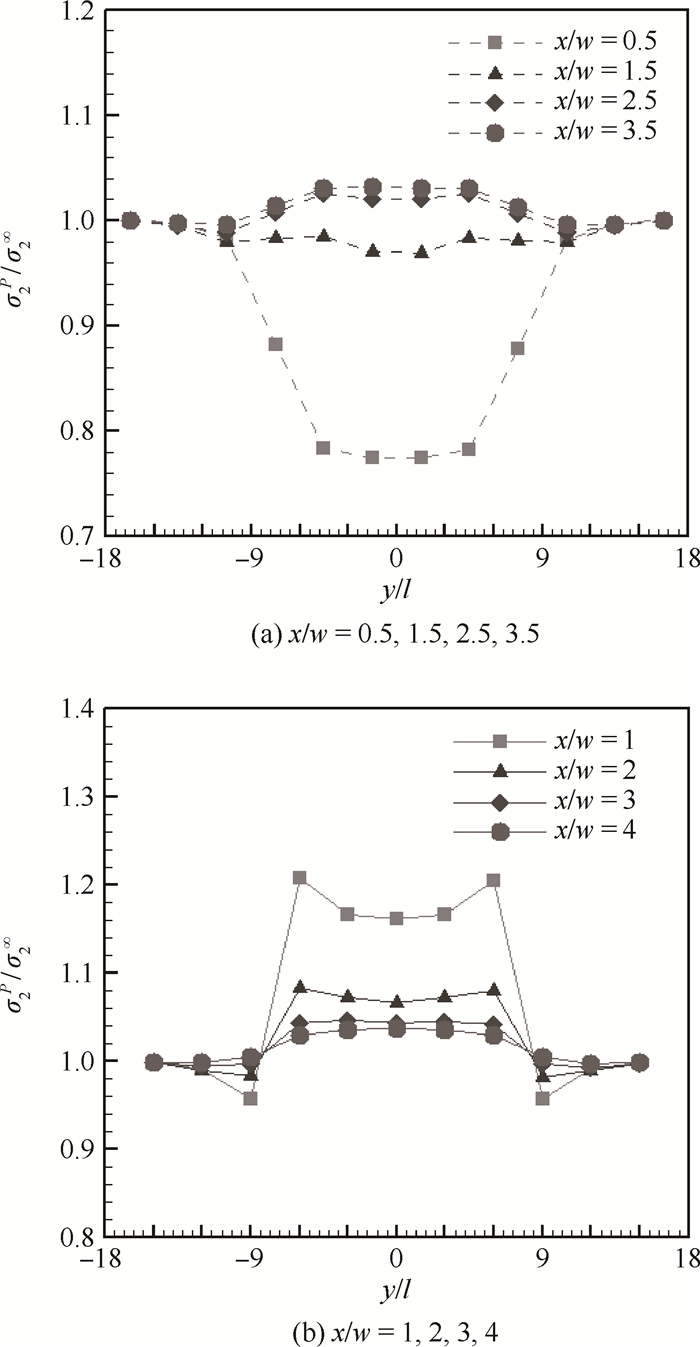
图 7所示为m=5,n=1的蜂窝壁拉应力分布,m=5,n=1所表示的缺陷为在蜂窝y向上的一个细长孔,即长轴平行于拉伸方向。此种受力状态下缺陷所导致的应力集中并不明显,在强度设计中也考虑较少,如图 7(a)所示。此类缺陷所受到的关注更多的在于均布拉力平行于x轴的受力条件,此时的蜂窝受力状态又回归到了类似于m=1,n=5的情形,故此类缺陷方式下的应力分布不再赘述。
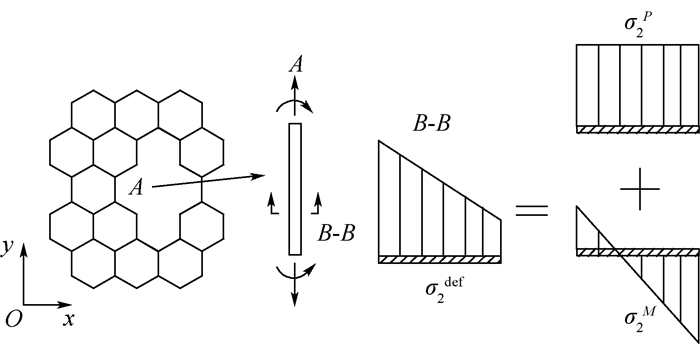
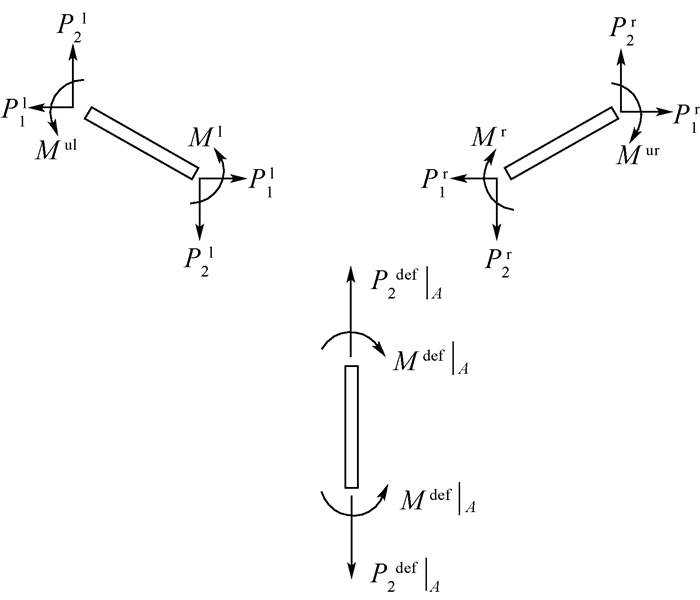
3 缺陷处最大弯曲应力解析分析以图 8缺陷构形为例,最大拉应力出现在胞壁A上,取如图 8所示的单元,建立图 9所示静力分析图,根据平衡条件有
|
| 图 8 最大拉应力所在胞壁应力分解 Fig. 8 Stress decomposition on cell wall with maximum tensile stress |
|
|
|
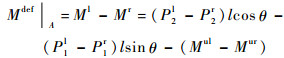
|
(8) |
式中: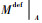
本文根据有限元计算结果证明了第2类缺陷类型满足:
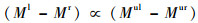
|
(9) |
式(9)代入式(8)得
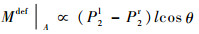
|
(10) |
本文采用文献[8]的方法,对P2l-P2r进行简化处理,用σ2P进行表示,本文发现在第2类缺陷存在的条件下,A处壁内弯矩大小满足式(11),与第1类缺陷不同。
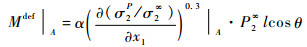
|
(11) |
式中:α为系数;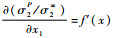
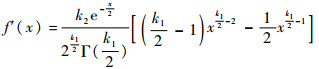
|
(12) |
通过式(11)和式(12)可以获得最大弯矩值与n的关系:
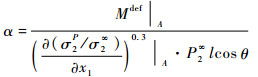
|
(13) |
通过图 10可以看出,对于不同的n值,α近似保持恒定,具体数值见表 3,α0为n=4时的α。因此,对于给定的n,式(14)可以预估缺陷危险点处的最大弯曲应力为
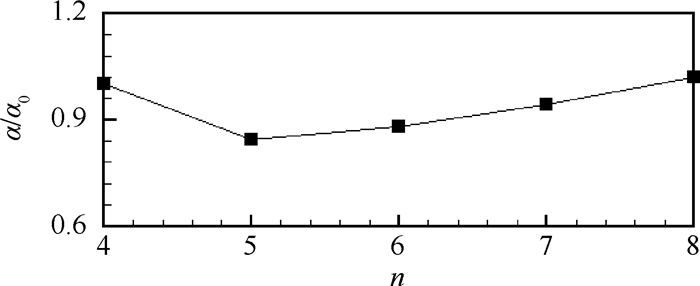
|
| 图 10 α/α0随n的变化关系 Fig. 10 Variation relationship of α/α0 with n |
| n | 4 | 5 | 6 | 7 | 8 |
| α/α0 | 1.000 0 | 0.844 2 | 0.880 0 | 0.943 3 | 1.019 8 |
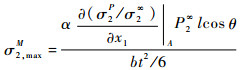
|
(14) |
式中:b为蜂窝高度。α虽近似稳定,但仍略有波动,并随n增大而先减后增,在n=5时达到最小值,这可能是由于n=5时所构成的缺陷形状相对于其他n值能够在一定程度上的削弱应力集中效应,如图 11[17]所示几种孔型应力集中,其强弱程度从上到下,从左到右依次递减,其几何尺寸更接近于图中的椭圆形孔5,而n=4则接近方形4,n>5则更接近细长型孔1、2和3。因此,当n=5时,对应的弯矩值相比其他值要略小。
4 结论1)本文的研究对象是以蜂窝壁缺失为缺陷类型的正六边形蜂窝结构。构建了一种新的缺失壁单元组合来定量描述缺陷大小,并建立了缺陷蜂窝有限元模型。
2)通过有限元与解析分析相结合的方法,本文发现缺失的蜂窝壁组合与应力分布有如下关系:在y=±(m-1)/2×3l的带状区上的壁内拉伸应力值明显高于周围蜂窝壁,最大应力出现在带状区内离缺陷孔最近的蜂窝壁上。
3)对于本文所构建的缺陷类型,根据有限元计算结果,本文给出了在距离缺陷孔x(x>0)处的蜂窝壁上的最大拉应力与完整(未存在缺陷)蜂窝的拉应力两者所存在的定量关系。
4)由于蜂窝壁缺失,导致临近缺陷孔处的壁内产生弯曲应力,本文考察了最大弯矩值与缺陷孔大小的定量关系,并针对本文所构建的缺失单元,推导出了最大弯曲应力值预估公式,对蜂窝预埋结构强度设计起指导作用。
| [1] | GIBSON L J, ASHBY M F. Cellular solids:Structure and properties[M]. 2nd ed Cambridge: Cambridge University Press, 1997 : 98 -135. |
| [2] | LI Y M, HOANG M P, ABBES F, et al. Analytical homogenization for stretch and bending of honeycomb sandwich plates with skin and height effects[J]. Composite Structures, 2015, 120 : 406 –416. DOI:10.1016/j.compstruct.2014.10.028 |
| [3] | LIU P, LIU Y, ZHANG X. Internal-structure-model based simulation research of shielding properties of honeycomb sandwich panel subjected to high-velocity impact[J]. International Journal of Impact Engineering, 2015, 77 : 120 –133. DOI:10.1016/j.ijimpeng.2014.11.004 |
| [4] | COELHO P G, RODRIGUES H C. Hierarchical topology optimization addressing material design constraints and application to sandwich-type structures[J]. Structural and Multidisciplinary Optimization, 2015, 52 (1) : 91 –104. DOI:10.1007/s00158-014-1220-x |
| [5] | LI S Q, LI X, WANG Z H, et al. Finite element analysis of sandwich panels with stepwise graded aluminum honeycomb cores under blast loading[J]. Composites Part A:Applied Science and Manufacturing, 2016, 80 : 1 –12. DOI:10.1016/j.compositesa.2015.09.025 |
| [6] | BARNETT D M, RAWAL S, RUMMEL K. Multifunctional structures for advanced spacecraft[J]. Journal of Spacecraft and Rockets, 2001, 38 (2) : 226 –230. DOI:10.2514/2.3674 |
| [7] | RAWAL S P, BARNETT D M, MARTIN D E. Thermal management for multifunctional structures[J]. IEEE Transactions on Advanced Packaging, 1999, 22 (3) : 379 –383. DOI:10.1109/6040.784489 |
| [8] | CHEN D H, OZAKI S. Stress concentration due to defects in a honeycomb structure[J]. Composite Structures, 2009, 89 (1) : 52 –59. DOI:10.1016/j.compstruct.2008.06.010 |
| [9] | CHEN T J, HUANG J S. Creep-buckling of hexagonal honeycombs with dual imperfections[J]. Composite Structures, 2009, 89 (1) : 143 –150. DOI:10.1016/j.compstruct.2008.07.018 |
| [10] | CHEN C, LU T J, FLECK N A. Effect of imperfections on the yielding of two-dimensional foams[J]. Journal of the Mechanics and Physics of Solid, 1999, 47 (11) : 2235 –2272. DOI:10.1016/S0022-5096(99)00030-7 |
| [11] | AJDARI A, NAYEB-HASHEMI H, CANAVAN P. Effect of defects on elastic-plastic behavior of cellular materials[J]. Materials Science and Engineering:A, 2008, 487 (1) : 558 –567. |
| [12] | ZHU K, CUI X D, FANG D N. The reinforcement and defect interaction of two-dimensional lattice materials with imperfections[J]. International Journal of Solids and Structures, 2012, 49 (13) : 1908 –1917. DOI:10.1016/j.ijsolstr.2012.04.002 |
| [13] | CUI X D, ZHANG Y H, ZHAO H. Stress concentration in two dimensional lattices with imperfections[J]. Acta Mechanica, 2011, 216 (1-4) : 105 –122. DOI:10.1007/s00707-010-0354-1 |
| [14] | LI K, GAO X L, SUBHASH G. Effects of cell shape and cell wall thickness variations on the elastic properties of two-dimensional cellular solids[J]. International Journal of Solids and Structures, 2005, 42 (5) : 1777 –1795. |
| [15] | WANG A J, MCDOWELL D L. Effects of defects on in-plane properties of periodic metal honeycombs[J]. International Journal of Mechanical Sciences, 2003, 45 (11) : 1799 –1813. DOI:10.1016/j.ijmecsci.2003.12.007 |
| [16] | 宋玉旺, 杨昌昊, 石晓飞, 等. 六边形蜂窝夹层板的参数化有限元建模方法[J]. 计算机辅助设计与图形学学报, 2015, 27 (1) : 175 –183. SONG Y W, YANG C H, SHI X F, et al. Parameterized finite element model of hexagon honeycombs[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27 (1) : 175 –183. (in Chinese) |
| [17] | LEYER A. Machine Design[M]. London: Blackie & Son, 1974 : 89 -92. |