2. 海军航空兵学院 兴城场站, 葫芦岛 125000
2. Xingcheng Station, Naval Air Force Institute, Huludao 125000, China
本文的研究对象是舰载k/N系统。所谓k/N系统,是指组成系统的N个单元中,只要正常工作的组件数多于k,系统就不会故障。对于舰船装备的维修保障而言,k/N系统是一种常见的重要功能产品,例如带有多个中继设备的舰船通信系统(6/8系统)、水面舰拖曳阵声呐中的潜水测音器阵列(58/64系统)和组成有源相控阵雷达的发射/接收阵列(2 700/3 000系统)等,其故障往往会产生任务性、安全性或重大经济性影响。另外,许多系统从结构上都可归类为k/N系统,例如并联系统可表示为1/N系统,而串联系统则可看作是N/N系统。
对于海上执行任务的舰船装备而言,维修保障是一项重要工作。对于如k/N系统这样的重要功能产品而言,如何确定维修策略,随舰携行多少备件,以及配备多少维修人员是保障部门经常面临的问题。在中国,这3个指标是由各分管部门各自优化确定的。然而在国外,文献[1]早就证明了维修计划与维修资源的联合优化会比分别优化节省保障成本;同时期的文献[2]也论证了将维修与备件联合优化会对总的保障成本产生巨大影响。考虑到中国越来越多的舰艇数量与日益频繁的出海频率,研究维修与携行备件的联合优化以降低维修保障的总费用是很有意义的。
当前的研究很少涉及到k/N系统,且大多都假设部件不可修,或假设维修发生时总有可用备件,很明显这些假设与实际是不符的。本文针对可修件的k/N系统开发了一个维修与携行备件的联合优化模型,讨论了传统边际分析法在求解模型时存在的问题,并针对这些问题给出了一种改进算法。
1 相关研究由于维修与备件这2个标准决定了联合优化问题,所以根据维修策略(批量维修、定期维修与视情维修)与备件的组合,可将相关研究分为3类。
1.1 批量维修与备件的联合优化Acharya等[3]针对一个具有n个独立同分布部件的系统,开发了一种批量维修与周期检查库存联合优化模型。模型忽略了延迟时间,使用了一种迭代程序来优化单周期模型与多周期模型的间隔期。该迭代程序从选择一个间隔增量和更换间隔期开始,每次迭代都会计算订购量上限和总成本。当迭代终止条件满足时,选择总成本最小的那组方案。
Chelbi和Ait-Kadi[4]利用卷积算法针对不同的设备寿命时间分布函数,计算了某一时间段内故障次数的均值和方差。尽管与Acharya等[3]的故障分布函数不同,但所使用的迭代程序非常相似,且都假设备件需求服从正态分布。
Brezavscek和Hudoklin[5]开发了一种用于机车电子机头的批量更换和周期检查联合模型,通过包含一个非零、确定性的延迟时间改进了Acharya等[3]的研究成果。
Huang等[6]通过引入随机延迟时间,不但改进了Brezavscek和Hudoklin[5]的模型,还证明了订购量上限为目标函数的唯一决策变量时,联合模型最小解的存在性和唯一性。
Panagiotidou[7]分析了n个同类型部件的联合优化问题,通过将故障分为主要故障和次要故障,建立了以单位时间成本最小为目标函数的优化模型,并给出了不同的维修方案与备件库存策略,是为数不多的研究不同程度故障对方案影响的文献。
Jiang等[8]研究了备件性能退化条件下的维修与备件联合优化。根据备件性能退化数据是否可得,分别建立了确定性和随机性2种退化模型,并以Brezavscek和Hudoklin[5]中的数据为例验证了模型的正确性和有效性。
1.2 定期维修与备件的联合优化Armstrong和Atkins[9]对定期更换与备件周期检查联合优化展开了研究,通过搜索更换时间和订货时间的最优组合,来使得总成本最小,并通过实例验证了分别优化比联合优化的成本要高3%。
Hu等[10]提出的工龄更换与备件库存联合优化模型采用了以下策略:定期更换部件并连续检查当前备件库存,若当前库存低于某一阈值则产生一次订货,订货量以库存达到某一设定值为准。模型采用仿真与遗传算法结合的优化方法,实验结果明显优于Kabir和Ahmed[2]提出的方案。
Lynch等[11]研究了预防性维修频率与备件的联合优化,利用遗传算法对决策变量进行求解,结果表明优化后的值每年可节省44%的保障成本。
1.3 视情维修与备件的联合优化Xie和Wang[12]对视情维修与备件联合优化进行了研究,将检查成本加入到成本计算公式中,提出的模型类似于Hu等[10]的模型,利用仿真与遗传算法的组合搜索联合策略的优化解,实例表明联合优化比分别优化的成本低3.78%。
Wang等[13-15]针对视情维修与备件联合优化进行了研究。文献[13]针对单部件系统开发了一个数学模型,并进行了分析计算,利用遗传算法计算了决策变量值。文献[14]将研究扩展到一组相同部件上。模型中系统的退化过程基于马尔可夫链,而对于决策变量的寻优则是利用蒙特卡罗仿真与枚举法的组合。文献[15]则采用基于遗传算法的仿真优化技术确定出连续检查库存(s, S)策略和视情维修策略的决策变量值。
Bjarnason等[16]针对k/N系统检修频率与备件库存联合优化问题,开发了一个优化模型,以故障件的可修率服从指数分布为条件对模型进行了仿真,并用算例证明了联合优化比分别优化更节省成本。
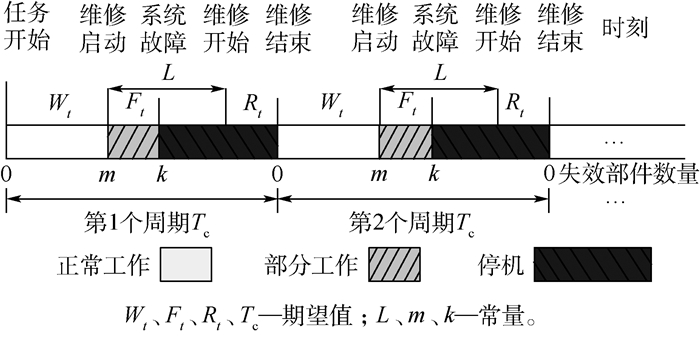
2 联合优化模型 2.1 问题描述与假设本节对k/N系统及其维修过程进行简要描述(见图 1)。在系统初始阶段,所有N个组件都是全新的。每个组件的故障过程独立同分布,均服从参数为λ的指数分布。系统中所有的N个组件故障都可通过状态监测监控到,只要系统中故障件的数目超过k,系统就会停机。为了尽量避免系统故障停机,设置当故障件数目m < N-k时启动维修。
|
| 图 1 k/N系统使用与维修过程 Fig. 1 Using and maintenance process of k-out-of-N system |
维修启动后,经过一段固定的维修准备时间L后,开始维修工作。在L这段时间内,系统照常工作,直到故障件数目超过k为止。在L期间,部件失效的数量AL服从参数为N-m与e-λt的二项分布。在系统维修阶段,维修人员将故障件用携行备件更换,且在计算过程中忽略更换所用时间。当没有可用备件时,维修人员立即对故障件维修,并将修复后的故障件做为备件使用。
当维修结束后,维修人员开始对更换下来的故障件维修,直至所有故障件维修完成或是达到下一次维修启动条件。单个维修人员修复故障件的修复时间独立同分布,均服从参数为μ的指数分布。
2.2 模型建立假设总的任务时长T是单个期望周期时长Tc的倍数,则使用可用度Ao可表示为单个Tc内k/N系统的期望工作时间(即至少有k个部件可用)除以Tc的期望值,即
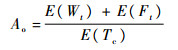
|
(1) |
式中:E(·)表示变量的期望值;Wt为从上次维修结束(或任务开始时刻)至下次维修启动的这段时间;Ft为从维修启动至维修开始这段时间内k/N系统正常工作的时间,且Ft为维修准备时间L的一部分。
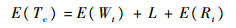
|
(2) |
式中:Rt为从维修开始至结束的工作时长。
Wt可分解为第1个部件的故障产生时间,第1个部件与第2个部件故障的时间间隔,……,以此类推,直至第m个部件故障结束。由于各部件的故障服从参数为λ的指数分布,根据指数分布的“无记忆性”可知,第i个部件与第i+1个部件之间的故障间隔时间服从参数(N-i)λ的指数分布。因此,Wt的期望值[17]可表示为
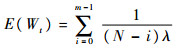
|
(3) |
从图 1中可见,Ft取决于m的大小与L期间部件失效的数量AL。m值越小,Ft的值就会越大;反之亦然。由于在L期间部件失效的数量AL服从参数为N-m与e-λt的二项分布,且部件的失效数量至多为N-m-k(此时系统失效),因此Ft的期望值[17]可表示为
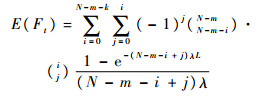
|
(4) |
E(Rt)取决于维修开始前的可用备件数量BR。由于本文忽略掉了备件更换时间,因此若维修开始前有BR≥m+AL,则有Rt=0。因此维修时长Rt主要是维修[m+AL-BR]+个故障件所花费的时间,其中,[x]+=max{x, 0}。假设配置了c个维修人员,故障件的维修时间相互独立,且均服从参数为μ的指数分布,则有[17]
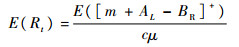
|
(5) |
由于AL服从参数为N-m与e-λt的二项分布,因此有
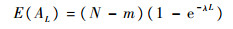
|
(6) |
下面计算BR。假设维修启动后维修人员即不再修复故障件,因此下次的BR值等于本次维修后剩余的可用备件[BR-m-AL]+,加上维修结束后到下次维修启动前这段时间内(即Wt)所修复的故障件数量Vc,同时又不可能超过上限S(因为存在没有故障件可修的可能性)。用式(7)表达这一关系为
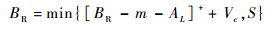
|
(7) |
c个维修人员在Wt这段时间内可修复的故障件个数Vc为
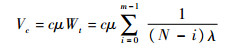
|
(8) |
对于费用方面,任务期间单位时间的期望成本Ctotal包括单位时间的备件储存与折旧成本Cstore、单个备件购置成本Cspare、单位时间的维修人员成本Cperson、一次维修的启动成本Cinit和单个故障件的更换成本Creplace。因此,Ctotal可表示为

|
(9) |
以典型的舰载k/N系统为例建立联合优化模型。当系统中的故障件m满足m≤N-k+1时启动一次维修;经过某一确定时间L后,利用携行备件执行故障件的更换工作;维修结束、系统重新启动后,维修人员开始维修更换下来的故障件以做为备件使用。在整个过程中,维修启动条件m、备件携行量S和维修人员数量c对整个过程具有较大影响,选为决策变量。目标函数是在给定某一使用可用度Ao下边界ψ的基础上,使得Ctotal的值最小,即
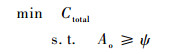
|
(10) |
求解式(10)的经典算法是边际分析法。这是一种著名的贪婪式启发算法,算法的每一步都通过比较选择单位投资产出最大效益的方案。第3节将分析算法在求解该模型时的缺点,并对这些缺点进行改进。
3 模型求解算法 3.1 边际分析法边际成本与边际收益是边际分析法的2个重要概念。边际成本是指每增加一个单位的产品所引起的成本增量,边际收益是指每增加一个单位产品所带来的收益增量。边际分析法的实质是研究边际收益关于边际成本的变化率。应用边际分析法求解式(10),主要步骤就是在每次迭代时,计算每个决策变量的边际变动,从中选择使用可用度增长最大的那一组。
在算法开始前,首先要确定决策变量的初始值。从逻辑上讲,使用可用度Ao是备件携行量S与维修人员数量c的递增函数,S与c越高,则Ao也越高。因此算法设置S=0与c=1为初始值,并在执行过程中递增。维修启动条件m的选择是在满足Ao≥ψ约束下使用维修间隔最大的m(即m的最大值)。因此算法初始设置m=N-k-1,并在执行过程中递减。
传统的边际分析法求解式(10)的步骤[18]如下:
Step 1根据使用要求设置使用可用度的下限ψ,初始化m=N-k-1,S=0,c=1,计算出Ao|m, S, c与Ctotal|m, S, c。
Step 2令m--;S++;c++。
Step3分别计算出Ao|m--, S, c、Ao|m, S++, c、Ao|m, S, c++,以及Ctotal|m--, S, c、Ctotal|m, S++, c、Ctotal|m, S, c++。
Step 4令(x, y, z)遍历集合{(m-1, S, c), (m, S+1, c), (m, S, c+1)},如果有一个或多个(x, y, z)使用Ao≥ψ成立,选择使得Ctotal|x, y, z最小的那组;否则选择使得(Ao|x, y, z-Ao|m, S, c)/(Ctotal|x, y, z-Ctotal|m, S, c)最大的那组(x, y, z)。
Step 5令m=x,S=y,c=z,Ao=Ao|x, y, z,若Ao < ψ成立,转向Step 3;否则,转向Step 6。
Step 6输出当前的m、S、c值,算法结束。
文献[18]在应用边际分析法时,求出的解与最优解之间存在较大差距,类似问题也存在于本文,具体见第4节中的算例。本文中边际分析法求解出的费用差异普遍在10%~30%之间,最大误差甚至接近60%。第3.2节将分析造成这一问题的原因,并针对这些问题进行改进。
3.2 存在的问题从模型建立与算法的处理过程来看,边际分析法性能较差的原因主要如下:
1)算法中c的步长。当c很小时,维修人员的利用率很高,那么增加c会对Ctotal与Ao产生很大的影响。例如,假设当c=1(c的最小值)时,维修人员的利用率为1.0,那么当c=2,利用率会降为0.4~0.5,即c的变化会对利用率产生很大影响,这一影响如此之大很难称之为“边际的”[18]。
2) S对Ao的影响是非单调的。在算法初始阶段,备件携行量S很小,远小于维修期间更换所需的期望数量时,备件的数量远远不够。此时,增加S的边际值对使用可用度Ao的影响很小。因此,算法不可能选择增加一个备件。取而代之的是尝试增加c或减小m。然而,随着S的增加,S的边际值对Ao的影响也会提高,携行更多的备件也更有吸引力。而当进一步增加S,超过实际所需时,边际值对Ao的影响又会减少。因此,Ao并不是S的凹函数,而这却是边际分析法所需要的。
3)假设算法运行到某步时得到的最优解为m=6,S=3,c=2,且下一步增加一个备件(S=4)时的边际收益最高。若模型的最优解为m=7,S=4,c=2,那么算法将不会搜索到该最优解,因为边际分析法不允许m增加。
4)当算法运行的初始阶段,m的值很高(初始设置m=N-k-1,为m的最高值),意味着预防性维修的频次很低,因此当需要维修作业时,往往会产生对维修人员的突发性大量需求,而这会使得算法倾向于增加维修人员的数量c。随着算法的运行,m值逐渐减小,对c的要求也降低,因此寻优过程应当减小c值,然而边际分析法却只允许增加该值,这就使得算法求得的c值过高。另外,对于备件携行量S也有类似的影响。
3.3 算法改进1)改进一:针对第3.2节问题1),在算法的初始阶段暂时不考虑增加c。只要算法计算出的费用值Ctotal在减少,且使用可用度Ao在增加,就只对m与S进行变化。这样,只在必要的阶段增加c值,减弱了c值对算法初期的影响力度,避免在算法初期导致c值增长过快。
2)改进二:针对第3.2节问题2),算法分为2步。首先以使用可用度约束ψ为目标值进行搜索;然后再以费用Ctotal最小为目标在Ao=ψ的附近搜索解空间。算法接受满足Ao≥ψ这一约束条件的所有解,并从中选择Ctotal最小的解,这样在第2步时避免了S对Ao的影响。
3)改进三:第3.2节中问题3)与问题4)需要综合考虑解决方法。问题3)中的“不允许m增加”,以及问题4)中m对c与S的影响,迫使算法降低m的初始值,并且c与S的初始值应当与m对应,以避免算法在初始阶段因变量之间的强相关性而错失最优解。
为达到这一目的,m的初始值minit应设置为最小值1;S的初始值Sinit应为图 1中单个周期Tc内的故障件数量,即
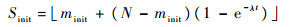
|
(11) |
式中: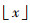
而c的初始值cinit应为满足Ao≥ψ这一约束条件下,维修Tc内产生的故障件数量所需要的维修人员数量,因此有
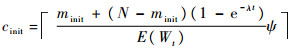
|
(12) |
式中:
4)改进四:第3.2节中问题1)~问题4)的一个共同原因是边际分析法的搜索路径是单条线的,算法对单条线的周围区域没有搜索。算法永远会沿着当前的边际效益值最大的解推进,而忽视了对整体效益值的考虑。为解决这一问题,应当在算法收敛时扩大搜索范围,为此本文提出了4个方向:
第1个措施是减小维修人员数量c,增加备件携行量S。前者会减少维修人员相关费用,后者会增加备件相关费用。算法的目的是在减小c的前提下,搜索S的最大值,以搜索是否在减少维修人员投资时存在更合理的备件配置方案。
第2个措施是减小维修人员数量c,且减小维修启动条件m。前者会减少维修人员相关费用,后者会增加维修相关费用。算法的目的是在减小c的前提下,搜索m的最小值,以搜索是否在减少维修人员投资时存在更合理的维修启动条件。
第3个和第4个措施与第1个和第2个措施相似。通过减小S增加c,以及减小S减小m,分别求解c的最大值与m的最小值,以分别平衡S与c及S与m的成本投入。
综上所述,给出改进后的边际分析法如下:
Step 1根据使用要求设置使用可用度的下限ψ,初始化m=1,S=Sinit,c=cinit,根据式(1)计算出Ao|m, S, c,根据式(9)计算出Ctotal|m, S, c。
Step 2令x=m+1,y=Sinit|m=m+1,z=c,并分别计算Ao|x, y, z与Ctotal|x, y, z。
Step 3若关系式Ao|x, y, z > Ao|m, S, c,Ctotal|x, y, z < Ctotal|m, S, c,m≤N-k-1同时成立,则令m=x,S=y,c=z,Ao|m, S, c=Ao|x, y, z,Ctotal|m, S, c=Ctotal|x, y, z,并转向Step 2;否则,转向Step 4。
Step 4若Ao|m, S, c≥ψ成立,转入Step 8;否则,转入Step 5。
Step 5暂不考虑c,搜索满足约束条件的S与m最大步进值。
Step 6计算Ao|m, S, c与Ctotal|m, S, c;令(x, y, z)遍历集合{(m, S, c), (m, S, c+1)},如果有(x, y, z)使得Ao≥ψ成立,选择使得Ctotal|x, y, z最小的那组;否则,选择使得(Ao|x, y, z-Ao|m, S, c)/(Ctotal|x, y, z-Ctotal|m, S, c)最大的那组(x, y, z)。
Step 7令c=z,转入Step 4。
Step 8令(x, y, z)遍历集合{(m, S+1, c-1), (m-1, S, c-1), (m-1, S-1, c), (m, S-1, c-1)},选择使得Ao≥ψ成立,且使得Ctotal|x, y, z最小的那组(x, y, z),若min{Ctotal|x, y, z} < Ctotal|m, S, c,则令m=x,S=y,c=z,Ao|m, S, c=Ao|x, y, z,Ctotal|m, S, c=Ctotal|x, y, z,并重新执行Step 8;否则,转入Step 9。
Step 9输出当前的m、S、c值,算法结束。
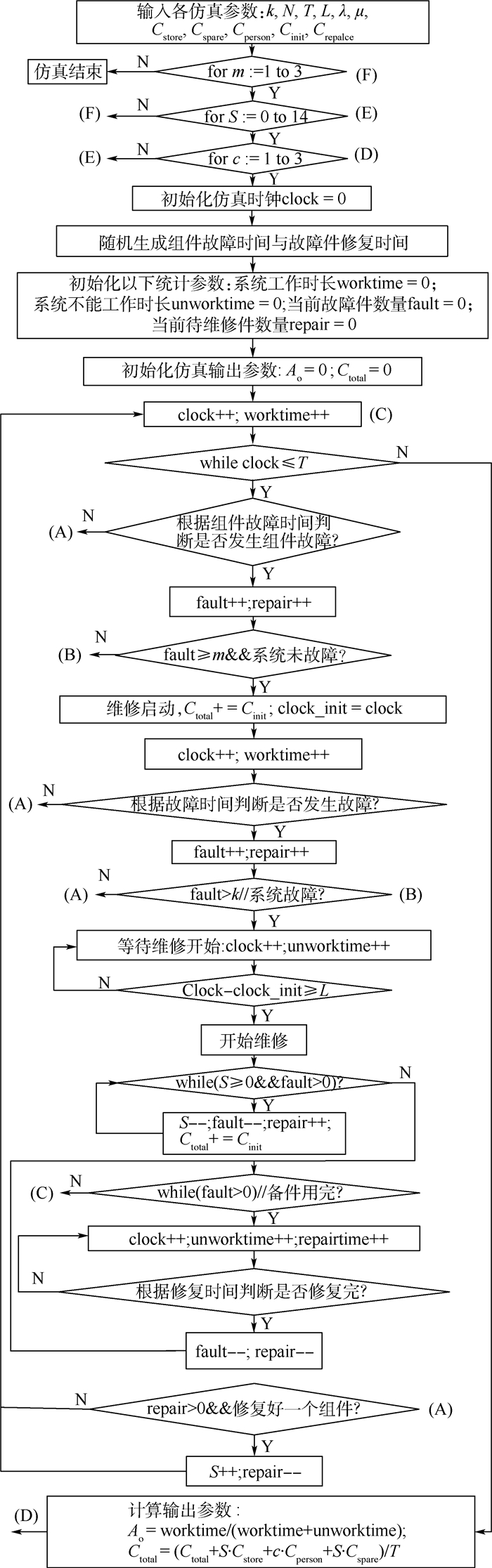
4 算例验证与分析 4.1 联合优化模型验证为了验证所建模型的正确性,以某型10/14系统为例,对维修保障过程进行了仿真,并将模型的计算结果与仿真值进行了比较。仿真流程如图 2所示,各参数设置如下:任务时长T=1 600,维修启动时长L=50,组件故障率λ=0.003,修复率μ=0.000 07,各费用参数分别为:Cstore=80,Cspare=100,Cperson=300,cinit=5 000,Creplace=100。仿真输入参数为3个决策变量,取值为m:1~3,S:0~14,c:1~3的组合,这样共可得到135组仿真值,仿真输出为10/14系统的使用可用度Ao与单位时间内的保障费用Ctotal。最后按式(13)~式(16)分别计算Ao与Ctotal的绝对误差均值与最大值:
|
| 图 2 仿真流程图 Fig. 2 Flowchart of simulation |
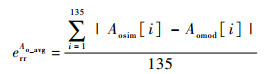
|
(13) |
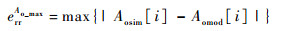
|
(14) |
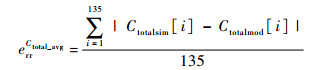
|
(15) |
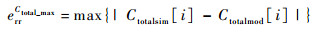
|
(16) |
表 1给出了Ao与Ctotal误差的统计分布情况、均值与最大值。可见,参数Ao的绝对误差主要出现在 < 0.04这一区间,其出现次数占了总统计数的56.3%,其中误差均值errAo_avg=0.036,最大误差errAo_max=0.092;而参数Ctotal的绝对误差大多出现在 < 150这一区间,其出现次数占了总统计数的62.96%,其中误差均值errCtotal_avg=145,最大误差errCtotal_max=287。
| 参数 | 统计分布情况(共135组) | 均值 | 最大值 | |
| 分布区间 | 出现次数 | |||
| errAo | < 0.02 | 43 | ||
| 0.02~0.04 | 33 | |||
| 0.04~0.06 | 27 | 0.036 | 0.092 | |
| 0.06~0.08 | 20 | |||
| > 0.08 | 12 | |||
| eCtotalrr | < 100 | 49 | ||
| 100~150 | 36 | |||
| 150~200 | 30 | 145 | 287 | |
| 200~250 | 14 | |||
| > 250 | 6 | |||
4.2 改进算法验证
为验证改进后算法的性能,以枚举法所求得的最优解为基准,以10/14系统、84/100系统和1 200/2 000系统为例,对边际分析法改进前后的寻优性能进行比较。对每类系统,分别运用传统的边际分析法与改进后的算法寻优,再分别以目标函数min{Ctotal}为参数计算与枚举法相对误差的百分比。为方便统计,本文以部件故障率、修复时间与各成本参数为基础,对每类系统组合出了128种案例(也可组合其他数量的案例,但原则上不能少于30组,以符合统计对大样本量的需要),各参数设置见表 2。
| 参数 | 10/14系统 | 84/100系统 | 1 200/2 000系统 |
| T | 1 600;16 000 | 2 000;20 000 | 4 000;40 000 |
| L | 50;100 | 100;200 | 200;400 |
| λ | 0.003;0.000 3 | 0.002;0.000 2 | 0.001;0.000 1 |
| μ | 0.000 07;0.000 007 | 0.000 05;0.000 005 | 0.000 03;0.000 003 |
| Cstore | 80;100 | 60;40 | 30;20 |
| Cspare | 100;150 | 50;30 | 20;15 |
| Cperson | 300;600 | 300;600 | 300;600 |
| Cinit | 5 000;10 000 | 8 000;16 000 | 20 000;40 000 |
| Creplace | 100;130 | 60;90 | 50;80 |
对于枚举法中各决策变量的上限值与下限值按以下方法处理:m、S和c下限值的设置与改进后算法的初始值相同,即分别为1、Sinit和cinit;而m的上限值自然设置为最大值N-k+1,S与c的上限值很难明确,这里分别设置为N与N-k-1。这一假设是合理的,因为携行N个备件覆盖了k/N系统的所有部件,而配置N-k-1个维修人员也保证了维修启动时每个故障件都有一个维修人员修理。
表 3以目标函数min{Ctotal}作为比较参数,给出了算法改进前后求得的解与枚举法最优解的平均误差与最大误差,以及这2种算法搜索到最优解的概率分布。可见,改进后算法的平均误差与最大误差下降很快,表明改进后的性能明显要优于未改进的边际分析法;同时改进后算法的寻优能力也有较大提高,3种系统的寻优能力分别提高了48.32%、48.71%和45.76%。
| 算法 | 指标 | 10/14系统 | 84/100系统 | 1 200/2 000系统 |
| 边际分析法 | 平均误差/% | 10.35 | 19.54 | 29.92 |
| 最大误差/% | 17.63 | 28.67 | 59.21 | |
| 寻优概率/% | 33.95 | 19.61 | 0 | |
| 改进算法 | 平均误差/% | 2.76 | 13.48 | 17.44 |
| 最大误差/% | 5.14 | 22.53 | 28.65 | |
| 寻优概率/% | 82.27 | 68.32 | 45.76 |
4.3 各改进项的贡献
本节测试第3.3节中4项改进措施的各自贡献。由于改进一与改进二很难分开处理,因此将这2处改进做为一个整体来测试。①对于改进一与改进二,将c与其他2个决策变量一同变化,并始终以满足约束条件下的费用最小做为寻优的方向;②对于改进三,将3个决策变量的初始值设置为m=N-k+1,S=0,c=1,且m恢复递减运算;③对于改进四,直接删除改进算法中的Step 8。将这3种情况分别求解第4.1节的算例,统计得到了表 4所示的数据。
| 项号 | 指标 | 10/14系统 | 84/100系统 | 1 200/2 000系统 |
| ① | 平均误差/% | 5.83 | 19.11 | 33.75 |
| 最大误差/% | 9.28 | 30.83 | 48.56 | |
| 寻优概率/% | 74.86 | 59.12 | 37.24 | |
| ② | 平均误差/% | 4.66 | 16.53 | 27.51 |
| 最大误差/% | 7.34 | 27.13 | 43.85 | |
| 寻优概率/% | 77.21 | 62.47 | 39.13 | |
| ③ | 平均误差/% | 3.91 | 15.23 | 20.62 |
| 最大误差/% | 8.62 | 26.96 | 35.77 | |
| 寻优概率/% | 80.19 | 64.19 | 40.83 |
对比表 3与表 4可以发现,4项改进措施对算法的性能较为显著。其中改进一与改进二(即表 3中的①)对寻优概率与目标函数误差的影响要高于其他2项(即表 4中的②与③),3种系统的寻优概率分别下降了7.41%、9.20%和8.52%;而改进四的影响最小,此时3种系统的寻优概率分别下降了2.08%、4.13%和4.93%。
5 结论本文工作有2项:一是以部件可修为前提,根据具体的使用与维修过程建立了k/N系统的维修与携行备件联合优化模型;二是为提高模型求解的准确度,分析了边际分析法求解模型的缺点,并针对这些缺点在传统算法的基础上进行了改进。根据算例验证表明:
1)与仿真结果相比,所建模型的误差较小,其中使用可用度的平均误差为0.036,保障总费用的平均误差为145。
2)改进边际分析法的性能提升较为显著,可有效降低平均误差与最大误差,提高寻优能力。
尽管本文针对的是海上执行任务的舰载系统,但对陆基装备在任务期间的维修保障也有一定的借鉴意义。进一步的研究方向包括考虑串件拼修、定期补给,以及将携行能力纳入约束条件下系统的维修保障,届时对于维修启动条件、备件携行量和维修人员数量这3个参数的权衡将会更加复杂,但也更贴近实战。
致谢
感谢海军航空兵学院的岳付昌为本文研究所提供的数据,感谢装甲兵工程学院试装大队的黄大山博士为本文仿真所做的具体指导。
| [1] | ARMSTRONG M, ATKINS D. Joint optimization of maintenance and inventory policies for a simple system[J]. IIE Transactions, 1996, 28 (5) : 415 –424. DOI:10.1080/07408179608966288 |
| [2] | KABIR A B M Z, AHMED S A. A stocking policy for spare part provisioning under age based preventive replacement[J]. European Journal of Operational Research, 1996, 90 (1) : 171 –181. DOI:10.1016/0377-2217(94)00246-0 |
| [3] | ACHARYA D, NAGABHUSHANAM G, ALAM S. Jointly optimal block-replacement and spare provisioning policy[J]. IEEE Transactions on Reliability, 1986, 35 (4) : 447 –451. DOI:10.1109/TR.1986.4335501 |
| [4] | CHELBI A, AIT-KADI D. Spare provisioning strategy for preventively replaced systems subjected to random failure[J]. International Journal of Production Economics, 2001, 74 (1-3) : 183 –189. DOI:10.1016/S0925-5273(01)00125-6 |
| [5] | BREZAVSCEK A, HUDOKLIN A. Joint optimization of block-replacement and periodic-review spare-provisioning policy[J]. IEEE Transactions on Reliability, 2003, 52 (1) : 112 –117. DOI:10.1109/TR.2002.805790 |
| [6] | HUANG R Q, MENG L L, XI L F, et al. Modeling and analyzing a joint optimization policy of block-replacement and spare inventory with random leadtime[J]. IEEE Transactions on Reliability, 2008, 57 (1) : 113 –124. DOI:10.1109/TR.2008.916887 |
| [7] | PANAGIOTIDOU S. Joint optimization of spare parts ordering and maintenance policies for multiple identical items subject to silent failures[J]. European Journal of Operational Research, 2014, 235 (1) : 300 –314. DOI:10.1016/j.ejor.2013.10.065 |
| [8] | JIANG Y P, CHEN M Y, ZHOU D H. Joint optimization of preventive maintenance and inventory policies for multi-unit systems subject to deteriorating spare part inventory[J]. Journal of Manufacturing Systems, 2015, 35 (1) : 191 –205. |
| [9] | ARMSTRONG M J, ATKINS D A. A note on joint optimization of maintenance and inventory[J]. IIE Transactions, 1998, 30 (2) : 143 –149. |
| [10] | HU R, YUE C, XIE J.Joint optimization of age replacement and spare ordering policy based on genetic algorithm[C]//Proceedings of the 2008 International Conference on Computational Intelligence and Security.Piscataway, NJ:IEEE Press, 2008:156-161. |
| [11] | LYNCH P, ADENDORFF K, YADAVALLI V S S, et al. Optimal spares and preventive maintenance frequencies for constrained industrial systems[J]. Computers & Industrial Engineering, 2013, 65 (3) : 378 –387. |
| [12] | XIE J, WANG H.Joint optimization of condition-based preventive maintenance and spare ordering policy[C]//Proceedings of the 4th International Conference on Wireless Communications, Networking and Mobile Computing.Piscataway, NJ:IEEE Press, 2008:6195-6199. |
| [13] | WANG L, CHU J, MAO W. A condition-based order-replacement policy for a single-unit system[J]. Applies Mathematical Modelling, 2008, 32 (11) : 2274 –2289. DOI:10.1016/j.apm.2007.07.016 |
| [14] | WANG L, CHU J, MAO W. An optimum condition-based replacement and spare provisioning policy based on Markov chains[J]. Journal of Quality in Maintenance Engineering, 2008, 14 (4) : 387 –401. DOI:10.1108/13552510810909984 |
| [15] | WANG L, CHU J, MAO W. A condition-based replacement and spare provisioning policy for deteriorating systems with uncertain deterioration to failure[J]. European Journal of Operational Research, 2009, 194 (1) : 184 –205. DOI:10.1016/j.ejor.2007.12.012 |
| [16] | BJARNASON E T S, TAGHIPOUR S, BANJEVIC D. Joint optimal inspection and inventory for a k-out-of-n system[J]. Reliability Engineering and System Safety, 2014, 131 (3) : 203 –215. |
| [17] | DE SMIDT-DESTOMBES K S, VAN DER HEIJDEN M C, VAN HARTEN A. On the availability of a k-out-of-N system given limited spares and repair capacity under a condition based maintenance strategy[J]. Reliability Engineering and System Safety, 2004, 83 (3) : 287 –300. DOI:10.1016/j.ress.2003.10.004 |
| [18] | DE SMIDT-DESTOMBES K S, VAN DER HEIJDEN M C, VAN HARTEN A. Joint optimisation of spare part inventory, maintenance frequency and repair capacity for k-out-of-N system[J]. International Journal of Production Economics, 2009, 118 (1) : 260 –268. DOI:10.1016/j.ijpe.2008.08.058 |



