2. 兰州理工大学 甘肃省工业过程先进控制重点实验室, 兰州 730050
2. Key Laboratory of Gansu Advanced Control for Industrial Processes, Lanzhou University of Technology, Lanzhou 730050, China
随着现代工业过程规模更加庞大,且系统内部联系变得更加紧密,对系统设备的可靠性和安全性研究受到了学术界的广泛关注[1-3]。故障诊断技术可对故障类型、故障部位及原因进行诊断,并为排除故障进而实现系统容错提供有力的科学依据和保障。现代设备结构复杂,系统或多或少存在非线性特性,工作现场噪声干扰严重,且不同于理想的高斯噪声。传统基于模型的非线性系统故障诊断方法,多采用非线性系统的模型线性化,与实际系统存在一定的误差,使得阈值的选取困难,故障诊断的误报率和漏报率较高。粒子滤波是递推贝叶斯估计的一种蒙特卡罗实现方法,利用蒙特卡罗的贝叶斯估计方法来逼近真实状态的后验概率密度[4-5],为解决非高斯噪声下非线性系统故障诊断提供了一种有效途径[6-8]。文献[9]针对移动机器人系统在线故障诊断难以及状态估计计算量大的问题,设计了一组基于非线性系统的平行粒子滤波器,提高了故障诊断效率,缩短了故障诊断时间。文献[10]使用粒子滤波结合极大似然估计和假设检验的方法,实现了非线性系统的故障检测,并进一步实现了对间歇故障的容错。文献[11]结合自适应模糊神经网络和高阶粒子滤波器,对非线性系统进行了故障预测,进而对系统进行了寿命预测。
粒子滤波的故障诊断方法,是利用粒子通过模型按时间顺序的前向传播估计系统状态值,并与系统状态真值比较产生残差,以残差作为故障诊断的依据[12]。然而,对于实际非线性系统而言,由于无法避免的建模误差、噪声及扰动等不确定性因素,残差势必会在一定范围内波动,因此在故障诊断中采用自适应阈值方法很有必要。针对基于模型的故障诊断,自适应阈值的选取通常有两种方法[13]:时域方法[14-15]和频域方法[16-17]。文献[15, 17]分别使用积分不等式和H∞输出观测器对一类线性系统分别采用时域方法和频域方法进行了自适应阈值的优化设计。但在非线性系统中,不管是针对结构不确定性的时域方法还是针对非结构不确定性的频域方法,局限性都比较大。因此,本文针对一类非线性系统,在深度分析了系统残差特性并得出其统计规律的基础上,利用统计方法设计自适应阈值,以此为依据使用粒子滤波算法对非线性系统进行了故障诊断,以期实现非线性系统的可靠故障诊断。
1 问题描述假设非线性系统状态空间模型描述如下:

|
(1) |
式中:xk为k时刻的系统状态;yk为在k时刻系统的输出测量值;uk为系统控制量;f和g为非线性函数;随机变量vk和wk为已知概率密度函数的状态噪声和测量噪声;θ为系统参数变量。
假设系统存在N种可能发生的故障,应用多模型的表述方法,系统有N+1种模型{Mi}i=0N,其中M0对应无故障情况,Mi(i=1, 2, …, N)表示第i种故障模型,则非线性系统状态空间模型可描述为
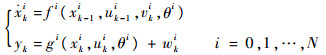
|
(2) |
其中:系统的测量噪声wki常为线性表示。
检测非线性系统(2)可能存在的故障,可通过预测系统输出值:
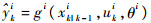
|
(3) |
式中:xk|k-1i为系统状态的一步预测值; ki为系统的输出预测值。由此可得系统的残差为
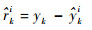
|
(4) |
如果系统未发生故障,则残差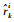
粒子滤波是动态系统状态估计的一种递归贝叶斯算法,实现对后验概率密度函数p(xk|y1:k)的计算。假设系统初始状态x0的先验分布p(x0|y0)已知,y1:k已知,y1:k为系统输出测量值,后验概率密度函数可通过以下两步得到。
1) 预测
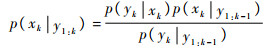
|
(5) |
2) 更新
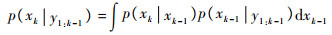
|
(6) |
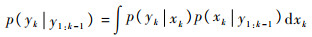
|
(7) |
在线性高斯系统中,概率密度函数由均值和协方差确定,利用卡尔曼滤波器就可以获取并进行更新。但对非线性非高斯系统,式(5)~式(7)中要求多个多维积分,很难获得解析解。因此利用近似算法来获得最优贝叶斯估计很有必要。
序列蒙特卡罗算法通过将积分运算转化为样本点的求和运算,后验概率密度函数p(xk|y1:k)便可由一些粒子xki及其权值ωki来近似:

|
(8) |
式中:δ(·)为狄拉克函数。
直接从后验概率分布中采样是很困难的,甚至是不可能的,可以从一个分布函数已知且易采样的分布函数q(xky1:k)中抽取样本,即采用重要性采样(IS)算法,分布q(xky1:k)称为重要性分布函数。为了便于递推计算,将重要性分布函数进行分解,可得到

|
(9) |
从式(9)中抽取样本,若系统状态服从马尔可夫过程并且在给定状态下观测值相互独立,可得重要性权值为
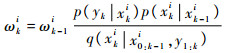
|
(10) |
将式(10)代入式(8)中,就得到对后验概率密度的估计。重要性权值即可迭代计算,此算法即是序贯重要性采样(SIS)算法。在SIS算法中,序贯重要性采样容易导致粒子数匮乏和退化,即在多次迭代后大量权值小的粒子被抛弃,重要性权值的分布变得趋于极端,这样就导致了无效的计算,影响后验概率密度的预测和更新。为了减轻退化的影响,Gordon提出对粒子样本进行重采样,对后验概率密度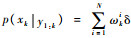
对非线性系统(2)进行故障诊断,检测系统中出现的残差是重要依据,从而识别是否有故障发生,进而对系统可能存在的N种故障进行故障分类。
3.1 故障检测根据模型分析,故障的发生多因θ参数的偏离引起,为了检测参数θ的变化,可检测测量输出似然函数p(y1:kθ)的变化,本文选用假设检验的方法:
H0:θ=θ0原假设,系统无故障
H1:θ≠θ0备择假设,系统有故障
其中:θ0为参数θ的真值。若满足θ=θ0时,认为原假设成立,无故障发生;当θ≠θ0时,认为备择假设成立,系统发生故障。
为了检测系统可能发生的故障,选取如下的对数似然函数:
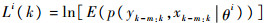
|
(11) |
式中:E为似然函数的数学期望。对最近的M个时刻Li(k)求和,则有
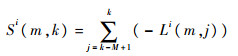
|
(12) |
利用粒子滤波的性质,可得
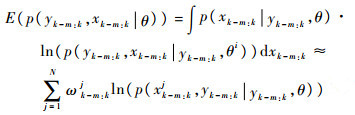
|
(13) |
式中:ωk-m:kj为使用粒子滤波状态序列估计的似然函数权值。由非线性状态空间的马尔可夫特性可得
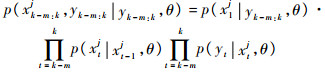
|
(14) |
将式(13)和式(14)代入式(11)即可求得对数似然函数Li(k)。
根据文献[19],对于给定的阈值δ,若似然函数值的对数和S(0)(m, k)>δ,则判定非线性系统发生故障。然而由于实际系统不可避免地存在建模误差、有色噪声及干扰等不确定性因素,若此时仍采用传统的固定阈值来判定故障的发生与否,很容易产生故障的误报和漏报。因此,若能依据系统不确定性的变化,采用自适应阈值势必会有更可靠的故障诊断效果。
3.2 自适应阈值设计以文献[19]中非恒温连续搅拌水箱式反应堆为研究对象,该系统是一个非线性系统,在反应器中通过添加一定温度、浓度的原料A,期望生成特定温度和浓度的生成物B。当系统发生温度传感器或流量传感器故障时,为了对系统进行可靠的故障诊断,有必要为其设计自适应阈值。
通过建立其数学模型,并观测输出测量值,可计算粒子滤波的输出预测值,代入式(4),可得系统残差。残差的计算是能否准确地实现故障检测和故障隔离的基础,而适当阈值的选取则是能否实现故障可靠诊断的保障。在系统存在内外不确定性的情形下,为了实现可靠故障诊断这一目标,需要对系统残差的特性进行进一步分析。在满足条件的不同扰动影响下,重复运行系统并测量系统的残差200次,可发现在每个时刻残差近似为0的测量值点数比较多,而当残差值逐渐远离0值时,测量值点数在逐渐减少。
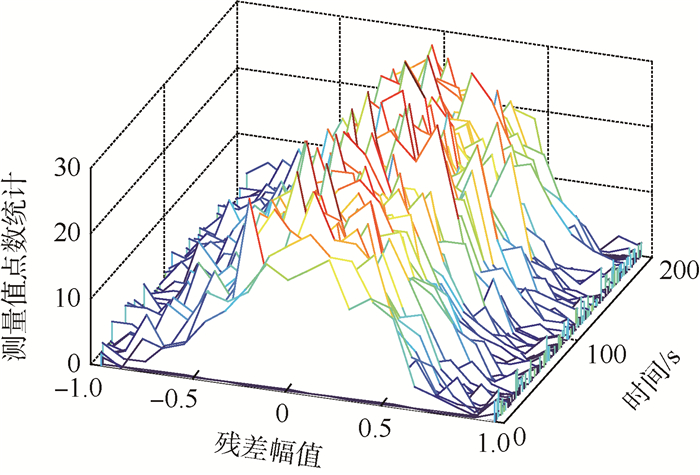
为了进一步分析,在采样周期确定的前提下,计算每个采样时刻的残差值,并将所得的残差值进行归一化处理,画出其直方图如图 1所示。
|
| 图 1 残差随随时间分布图 Fig. 1 Distribution of residual error versus time |
从图 1可得,每一个时刻,当残差值近似为0值时,直方图中分布的测量值点数较多,而当残差幅值逐渐上升时,测量值点数逐渐趋于0,符合正态分布的典型特征。通过Lilliefors假设检验可得显著性水平为0.02,说明残差的分布确实可近似为正态分布。
参考随机过程理论知识[20]与文献[21],可设计残差的期望与方差:
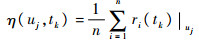
|
(15) |
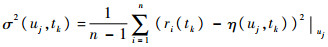
|
(16) |
式中:η(uj, tk)为输入为uj时tk时刻残差的均值; σ2(uj, tk)为输入为uj时tk时刻残差的方差; n为系统重复运行并测量系统残差的次数。
若设显著性水平为α=0.03,即置信度为97%,则相关系数为z=2.17,满足:
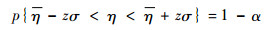
|
(17) |
由此可得自适应阈值计算如下:
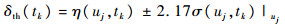
|
(18) |
可见,只要残差统计特性满足正态分布,即可用上述方法设计自适应阈值,一般情况下残差统计特性往往都满足正态分布特性。由于该方法不依赖于系统数学模型,因此在系统自适应阈值设计中更易于实现。
当系统发生故障时,系统残差是由故障信息及建模误差、噪声、扰动等不确定性因素造成的,同时也影响系统阈值的选取。然而,系统在多次运行中,即使是在运行时间段中的相同时刻,阈值也可能受到不同工况、不同外部条件的影响。如表 1所示为电动液压系统在不同运行情况下残差偏差的采样值[21],可见阈值在不同外部环境的影响下会发生偏差。故自适应阈值也应相应地做出调整:
| 阈值偏差 | u1 | u2 | u3 | u4 |
| φ1 | -0.0000 | -0.0047 | -0.0101 | -0.0092 |
| φ2 | 0.0303 | 0.4441 | 0.9822 | 0.9300 |
| φ3 | 0.0019 | -7.2248 | -18.4420 | -16.0660 |

|
(19) |
式中:ψT和φT分别为不同外部条件作用下均值和方差的修正值。不同外部环境下,方差波动通常变化不大,故设φT=1。在输入值确定的情况下,均值波动ψT的选取可通过不同外部环境下运行的数值,经过多次运行采样后求取均值得到: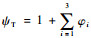
即使检测到明显故障信息,通常也较难从中获取足够的数据来识别是何种故障,且系统可能同时发生多种故障,因此故障隔离通常比故障检测更为复杂。本文将可能发生的故障设为故障集{Mi}i=0N,并假设任意两种故障不会同时发生。当系统同时发生故障M1和M2时,将此故障设定为M1, 2并加入故障集。
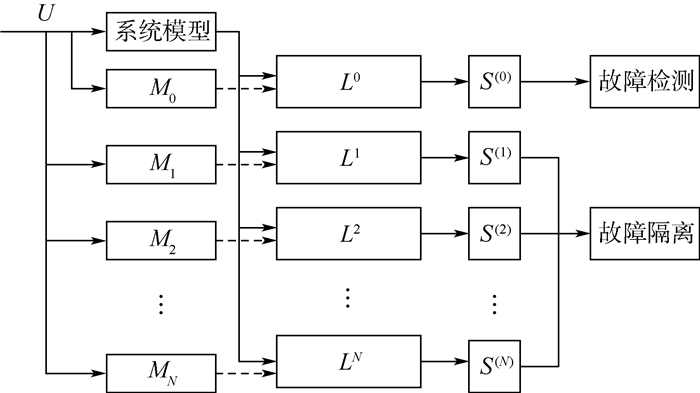
为了识别具体的故障模型,需要一系列的平行粒子滤波器,并计算出相应的对数似然函数Li(k),当残差比较小时,实际系统模型与该故障模型匹配,而其他模式的残差将比较大。图 2为故障检测与故障隔离原理图[20]。
|
| 图 2 故障诊断原理图 Fig. 2 Principle of fault diagnosis |
故障诊断方法是故障检测、定位的有效手段,但由于系统可能存在的建模误差、噪声等不确定因素的影响,故障误报和故障漏报很难避免。
在评价故障诊断系统的有效性中,故障误报率和故障漏报率是两个重要指标。参考文献[22]中故障漏报率pm和故障误报率pf的计算方法:
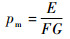
|
(20) |
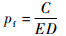
|
(21) |
系统共运行F次。发生故障时若残差小于阈值,发生的次数记为E;系统一次运行的总点数记为G;系统无故障发生,且残差值大于阈值的时间点总个数记为C;系统无故障时的时间点总个数记为D。
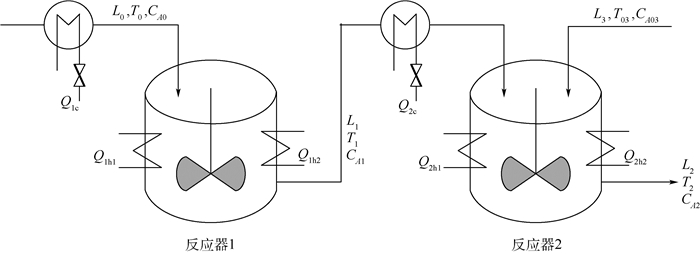
4 仿真分析参考文献[19]中系统模型,本文所采用的仿真对象为非恒温连续搅拌水箱式反应堆(CSTR),如图 3所示。该对象的反应器发生3个不可逆的基本发热反应,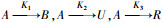
|
| 图 3 非恒温连续搅拌水箱式反应堆 Fig. 3 Non-constant temperature continuous stirred tank reactor |

|
(22) |
式中:Ri(CAj, Tj)=ki0exp(-Ei/RTj)CAj(j=1, 2);T、CA、Q和V分别为反应器温度、反应剂A的浓度、反应器的热传递比率和反应器的体积;ΔHi、ki和Ei(i=1, 2, 3)分别为3种反应的热含量、指数常数和反应触发能量;cp和ρ分别为反应器的热容量和流体密度。反应堆稳定时各参数值如表 2所示。
| 参数 | 数值 |
| L0/(m3·h-1) | 4.998 |
| L1/(m3·h-1) | 4.998 |
| L3/(m3·h-1) | 8 |
| V1 /m3 | 1 |
| V2 /m3 | 3 |
| R /(kJ·kmol-1) | 8.314 |
| T0 /K | 280 |
| T03 /K | 280 |
| CA0s /(kmol·m-3) | 2.4 |
| CA03s /(kmol·m-3) | 2.6 |
| Q1s /(kJ·h-1) | 0.7×106 |
| Q2s /(kJ·h-1) | 0.3×106 |
| Δ H1 /(kJ·kmol-1) | -1.00×105 |
| Δ H2 /(kJ·kmol-1) | -1.04×105 |
| Δ H3 /(kJ·kmol-1) | -1.08×105 |
| k10 /h-1 | 3.0×106 |
| k20 /h-1 | 3.0×105 |
| k30 /h-1 | 3.0×105 |
| E1 /(kJ·kmol-1) | 5.0×104 |
| E2 /(kJ·kmol-1) | 7.53×104 |
| E3 /(kJ·kmol-1) | 7.53×104 |
| ρ /(kg·m-3) | 2000 |
| cp /(kJ·kg-1) | 0.731 |
| T1s/K | 424.4 |
| T2s /K | 444.5 |
| CA1s/(kmol·m-3) | 1.69 |
| CA2s/(kmol·m-3) | 0.89 |
设非线性系统的测量噪声和系统噪声方差阵为

|
考虑该非线性系统可能存在的4种故障模式, 如表 3所示。
| 故障 | 稳态值 | 故障值 |
| F1:温度传感器偏差T0 /℃ | 280 | 295~311 |
| F2:流量传感器偏差L0 / (m3·h-1) | 4.998 | 5.25~5.5 |
| F3:温度传感器偏差T03 /℃ | 280 | 295~311 |
| F4:流量传感器渐变故障L1 / (m3·h-1) | 4.998 | 4.998(1-β) |
| 注:β—传感器失效率。 | ||
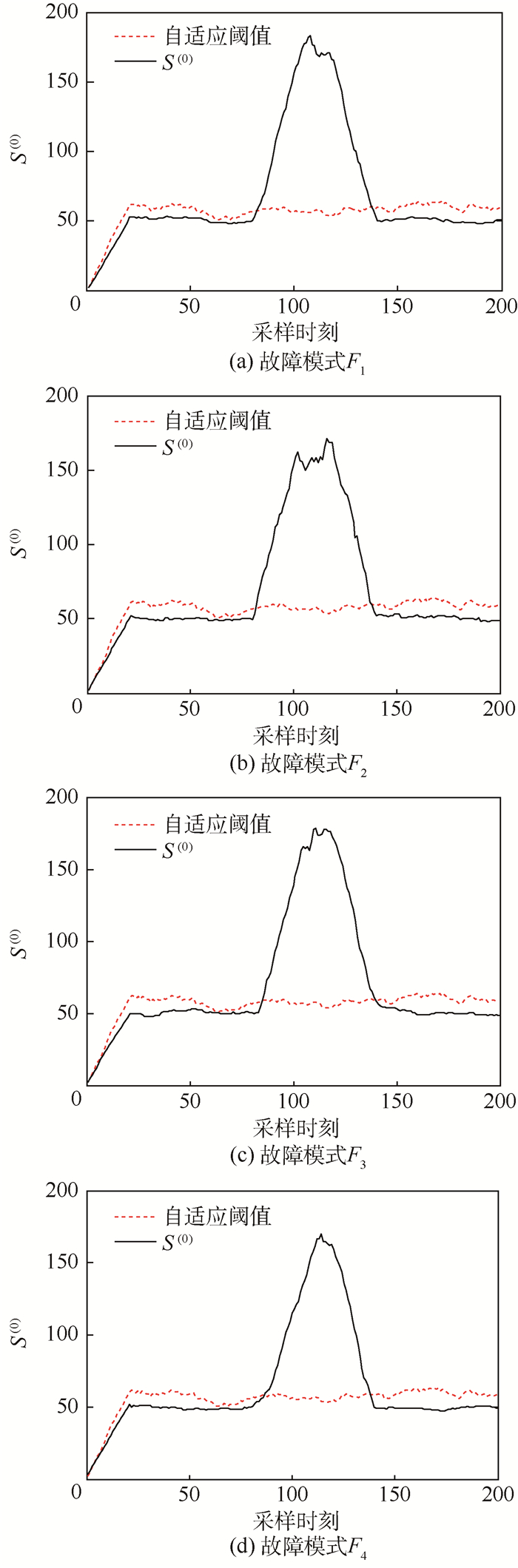
针对上述4种故障模式,应用本文中所述的故障检测方法,故障F1、F2和F3为传感器偏差故障,发生在采样时刻80~140。故障F4为传感器渐变故障,模拟传感器失效过程。在采样时刻80~100,β=2%;在采样时刻100~120,β=3%;在采样时刻120~140,β=5%。采用3.1节和3.2节描述的基于对数似然函数值和的故障检测方法,检测结果见图 4。由图可知,当系统未检测到故障时,S(0)较小;当系统检测到故障时,S(0)增大。由于本文在故障诊断过程中采用了自适应阈值方法,无需提前设定阈值,系统可根据残差计算自适应阈值,实现系统的故障检测。
|
| 图 4 故障模式F1、F2、F3和F4检测 Fig. 4 Detection of failure mode F1, F2, F3 and F4 |
对于固定阈值的选取,其选取的基本原则是:尽可能把正常工作的值包含在阈值之内,一旦残差信号超过给定阈值,则系统处于异常工作状态的可能性最大。本例采用固定阈值选取的阈值均方根法,将4种故障情况下的允许误差综合起来考虑,每个通道考虑其允许的最大误差Wi,最后确定出最坏情况下所允许的偏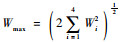
应用式(20)计算固定阈值与自适应阈值情形下的故障漏报率,比较结果如表 4所示。
| 故障 | 漏报率 | |
| 阈值δ=65 | 自适应阈值 | |
| F1:温度传感器偏差T0 | 0.1287 | 0.0865 |
| F2:流量传感器偏差L0 | 0.1043 | 0.0887 |
| F3:温度传感器偏差T03 | 0.1276 | 0.0564 |
| F4:流量传感器渐变故障L1 | 0.2190 | 0.1007 |
一旦检测到故障信息后,比较4种故障模式的对数似然函数和S(1)、S(2)、S(3)和S(4)可对故障进行隔离,当与故障模式匹配时,对数似然函数和较小,否则对数似然函数和较大,结果如图 5所示。

|
| 图 5 故障模式F1、F2、F3和F4隔离 Fig. 5 Isolation of failure mode F1, F2, F3 and F4 |
1) 粒子滤波是解决非线性系统故障诊断的一种有效手段,采用对数似然函数和作为评价指标,可以实现非线性系统的故障检测和故障隔离。
2) 阈值的设计是非线性系统故障诊断的基础,利用统计特性设计残差的阈值可以避免非线性系统模型中的复杂因素,且采用自适应阈值可有效地降低故障诊断的漏报率和误报率。
3) 本文通过统计方法得到残差特性满足正态分布特性,只要满足正态分布特性的残差,就可通过本文设计的方法实现自适应阈值的设计。
| [1] | GERTLER J J. Fault detection and diagnosis in engineering systems[M]. New York: Marcel Dekker, Inc., 1998 : 36 -58. |
| [2] | GHANTASALA S, EL-FARRA N H. Robust actuator fault isolation and management in constrained uncertain parabolic PDE systems[J]. Automatica, 2009, 45 (10) : 2368 –2373. DOI:10.1016/j.automatica.2009.06.024 |
| [3] | FENG K, JIANG Z, HE W. Rolling element bearing fault detection based on optimal antisymmetric real Laplace wavelet[J]. Measurement, 2011, 44 (9) : 1582 –1591. DOI:10.1016/j.measurement.2011.06.011 |
| [4] | TAFAZOLI S, SUN X. Hybrid system state tracking and fault detection using particle filters[J]. IEEE Transactions on Control Systems Technology, 2006, 14 (6) : 1078 –1087. DOI:10.1109/TCST.2006.883193 |
| [5] | MICHELE C, PIERO B, PIETRO T, et al. Interacting multiple-models, state augmented particle filtering for fault diagnostics[J]. Probabilistic Engineering Mechanics, 2015, 40 : 12 –24. DOI:10.1016/j.probengmech.2015.01.001 |
| [6] | 杜京义, 殷梦鑫. 一种改进的粒子滤波算法应用于故障诊断[J]. 系统仿真学报, 2014, 26 (1) : 62 –66. DU J Y, YIN M X. Improved algorithm of particle filter applied to fault diagnosis[J]. Journal of System Simulation, 2014, 26 (1) : 62 –66. (in Chinese) |
| [7] | ZHANG B, SCONYERS C, BYINGTON C, et al. A probabilistic fault detection approach:Application to bearing fault detection[J]. IEEE Transactions on Industrial Electronics, 2011, 58 (5) : 2011 –2018. DOI:10.1109/TIE.2010.2058072 |
| [8] | WEI T, HUANG Y, CHEN C. Adaptive sensor fault detection and identification using particle filter algorithms[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C:Applications and Reviews, 2009, 39 (2) : 201 –213. DOI:10.1109/TSMCC.2008.2006759 |
| [9] | MICHAL Z. Online fault detection of a mobile robot with a parallelized particle filter[J]. Neurocomputing, 2014, 126 : 151 –165. DOI:10.1016/j.neucom.2012.11.049 |
| [10] | TADIC' P, DUROVIC' Z. Particle filtering for sensor fault diagnosis and identification in nonlinear plants[J]. Journal of Process Control, 2014, 24 (4) : 401 –409. DOI:10.1016/j.jprocont.2014.02.009 |
| [11] | CHEN C C, GEORGE V C, MARCOS E. Machine remaining useful life prediction:An integrated adaptive neuro-fuzzy and high-order particle filtering approach[J]. Mechanical Systems and Signal Processing, 2012, 28 : 597 –607. DOI:10.1016/j.ymssp.2011.10.009 |
| [12] | YU J. A particle filter driven dynamic Gaussian mixture model approach for complex process monitoring and fault diagnosis[J]. Journal of Process Control, 2012, 22 (4) : 778 –788. DOI:10.1016/j.jprocont.2012.02.012 |
| [13] | VICENC P, SAUL M D, JOAQUIM B. Adaptive threshold generation in robust fault detection using interval models:Time-domain and frequency-domain approaches[J]. Interational Journal of Adaptive Control and Signal Process, 2013, 27 (10) : 873 –901. |
| [14] | JOHNSON A L.A new algorithm for adaptive threshold generation in robust fault detection based on a sliding window and global optimization[C]//Proceedings of European Control Conference 1999, ECC'99. Piscataway, NJ:IEEE Press, 1999:1546-1551. |
| [15] | JOHANSSON A, BASK M, NORLANDER T. Dynamic threshold generators for robust fault detection in linear systems with parameter uncertainty[J]. Automatica, 2006, 42 (7) : 1095 –1106. DOI:10.1016/j.automatica.2006.02.009 |
| [16] | DING X, FRANK P M.Frequency domain approach and threshold selector for robust model-based fault detection and isolation[C]//IFAC/IMACS Symposium on Fault Detection, Supervision and Safety for Technical Processes-SAFEPROCESS'91. Tarrytown, NY:Pergamon Press Inc., 1992:271-276. |
| [17] | RAMBEAUX F, HAMELIN F, SAUTER D. Optimal thresholding for robust fault detection of uncertain systems[J]. International Journal of Robust and Nonlinear Control, 2000, 10 (4) : 1155 –1173. |
| [18] | GORDON N J, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEEE Proceedings on Radar and Signal Processing, 1993, 140 (2) : 107 –113. DOI:10.1049/ip-f-2.1993.0015 |
| [19] | ALROWAIE F, GOPALUNI R, KWOK K. Fault detection and isolation in stochastic non-linear state-space models using particle filters[J]. Control Engineering Practice, 2012, 20 (10) : 1016 –1032. DOI:10.1016/j.conengprac.2012.05.008 |
| [20] | BHATTACHARYA R, WAYMIRE E C. Stochastic processes with applications[M]. New York: Wiley, 1990 : 40 -55. |
| [21] | SHI Z, GU F, LENNOX B, et al. The development of an adaptive threshold for model-based fault detection of a nonlinear electro-hydraulic system[J]. Control Engineering Practice, 2005, 13 (11) : 1357 –1367. DOI:10.1016/j.conengprac.2004.11.014 |
| [22] | KADIRKAMANATHAN V. Particle filtering-based fault detection in non-linear stochastic systems[J]. International Journal of Systems Science, 2002, 33 (4) : 259 –265. DOI:10.1080/00207720110102566 |



