2. 肯特大学 数学、统计与精算学院, 坎特伯雷 CT27NZ;
3. 北京大学 数学科学学院, 北京 100871
2. School of Mathematics, Statistics and Actuarial Science, University of Kent, Canterbury CT27NZ, United Kingdom ;
3. School of Mathematics, Peking University, Beijing 100871, China
捕食者-食饵系统是生态系统的基本组成部分之一,它们的交互作用在保持生态稳定性方面具有不可忽略的影响。许多生物种群,同时扮演着捕食者和食饵的角色,即与其他生物种群一起,构成庞大复杂的食物链。对3种群及3种群以上的食物链模型已有大量的研究结果。实验和理论研究表明,即使结构极其简单的食物链系统,也会表现出丰富的动力学特性[1-6]。这些性质都体现出物种之间具有非常复杂的交互作用和影响,某一物种条件改变有可能引起其他种群数量的变化,牵一发而动全身。
对自然界的很多捕食者来说,它们并不是以单一食饵为食,可能会由于季节更替、种群迁徙、食饵丰富程度等原因选择不同的食饵[7-8]。因此,近年来,生态学家、生物学家对捕食者,特别是食物链顶端捕食者可供选择的食饵增加时所产生的后果进行了大量的研究[9-15]。研究发现,可供选择的食饵的数量、质量等因素都可能会在系统的稳定性、持久性等方面起到决定性作用[11-15]。
本文对由食饵、中间捕食者和顶级捕食者构成的三维食物链系统建立相应的数学模型,其中假设中间捕食者还有其他可供选择的食饵。对模型的平衡点存在性、稳定性以及Hopf分支等性质展开深入的理论分析和数值模拟,从中得到食饵选择性对整个生态系统的动力学影响。
1 模型的建立经典的三维Hastings-Powell食物链模型[2]表示为如下的方程组:
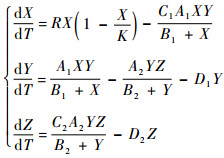
|
(1) |
式中:X(T)、Y(T)和Z(T)分别为食饵、中间捕食者和顶级捕食者在时刻T的数量;R为食饵的自然增长率;K为环境所能容纳的食饵最大数量;C1-1和C2分别为食饵X(T)能量向捕食者Y(T)和Z(T)增长率转化的转化率;Ai、Bi和Di分别为两捕食者的最大捕食率、半饱和常数和死亡率。
假设中间捕食者除食饵X(T)之外,还有其他可供选择的食饵,则可将上述模型改写为如下形式:
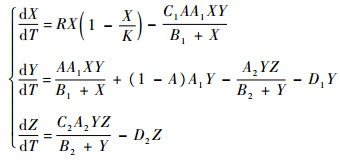
|
(2) |
在第2个方程中,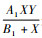
将式(2)进行无量纲化处理,令
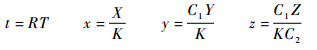
|
则系统式(2)改写为如下形式:
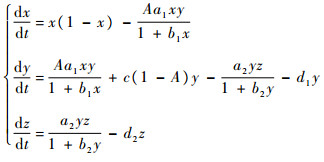
|
(3) |
式中:
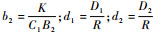
下面将对系统式(3)展开动力学性质的研究。
2 平衡点的存在性和稳定性 2.1 边界平衡点的存在性和稳定性分析易知,系统具有如下3种类型的边界平衡点:
1) (0,0,0),即3种群数量均为0。此时模型在平衡点处的雅可比行列式为
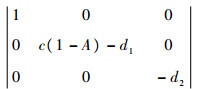
|
此行列式有一个正的特征根1,故对应的平衡点不稳定。
2) (1, 0, 0),即食饵数量达到最大值,中间捕食者和顶级捕食者种群数量为零,雅可比行列式为

|
当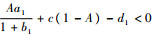
3) (x, y, 0),即只有顶级捕食者数量为0,而中间捕食者和食饵数量非0。由方程组
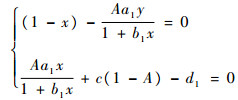
|
解得

|
(4) |
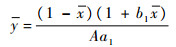
|
(5) |
因此当0 < x < 1时此平衡点存在。
令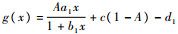
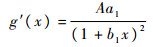
|
故g(x)在x>0时单调递增,从而有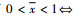
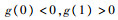
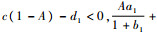
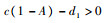
在平衡点处的雅可比行列式为
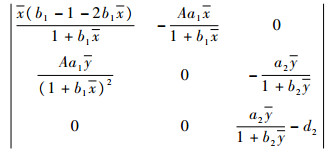
|
当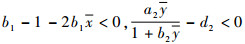
将式(4)代入不等式b1-1-2b1x < 0可得

|
综上所述,得到如下结论。
定理1 当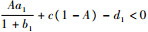
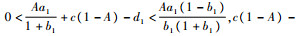

定理2 假设
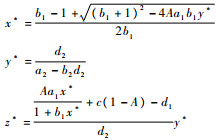
|
当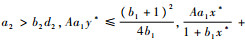
证明 在定理假设下,y*>0。求解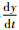
由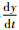
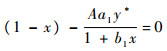
|
即抛物线y=(1-x)(1+b1x)和直线y=Aa1y*的交点处横坐标。
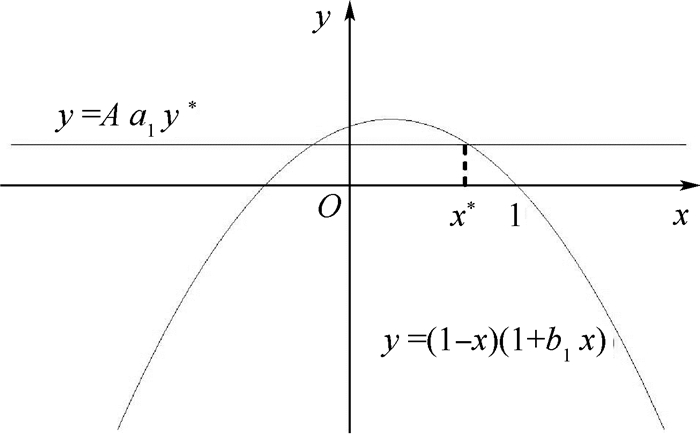
如图 1所示,当
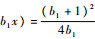
|
| 图 1 内部平衡点的存在性 Fig. 1 Existence of interior equilibrium point |
令系统式(3)中的第2个方程右端为0,代入x*和y*,可得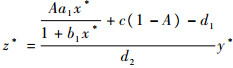
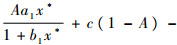
综上所述,(x*, y*, z*)为系统式(3)的一个内部平衡点。
2.2.2 内部平衡点(x*, y*, z*)的稳定性内部平衡点处的雅可比行列式为
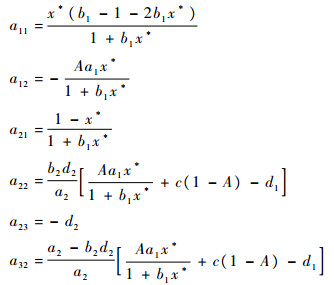
|
特征方程为λ3+P1λ2+P2λ+P3,其中:
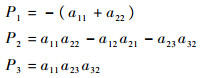
|
因为x*在抛物线y=(1-x)(1+b1x)的顶点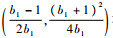
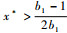
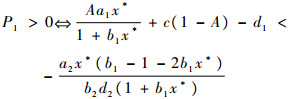
|
对P1P2-P3进行化简:

|
式中:
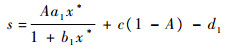
|
(6) |
抛物线f(s)满足
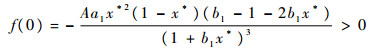
|
和
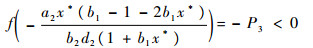
|
故此函数曲线只可能是图 2的两种情况之一。必存在点

|
| 图 2 抛物线f(s)的图像 Fig. 2 Graph of parabola f(s) |
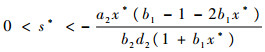
|
使得f(s*)=0,当s < s*时,f(s)>0,P1P2>P3和P1>0成立。由Routh-Hurwitz定理可知,
此时内部平衡点(x*, y*, z*)是局部渐进稳定的。
假设方程λ3+P1λ2+P2λ+P3=0有一对纯虚根±iω,将根代入可得ω=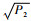
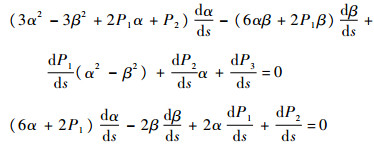
|
因此,
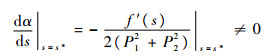
|
这表明在s=s*处存在Hopf分支。
定理3 假设定理2的条件成立,则存在
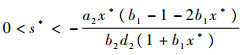
|
满足f(s*)=0。当0 < s < s*时,内部平衡点局部渐进稳定,在s=s*处系统存在Hopf分支。
3 Hopf分支的数值仿真定理3给出了系统的动力学性质随s取值不同而改变的特性,改变系统的相应参数值,可使s的取值满足定理中的条件。例如,由表达式(6)可知, s的值随c的增加而增大,s=s*对应于
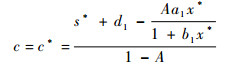
|
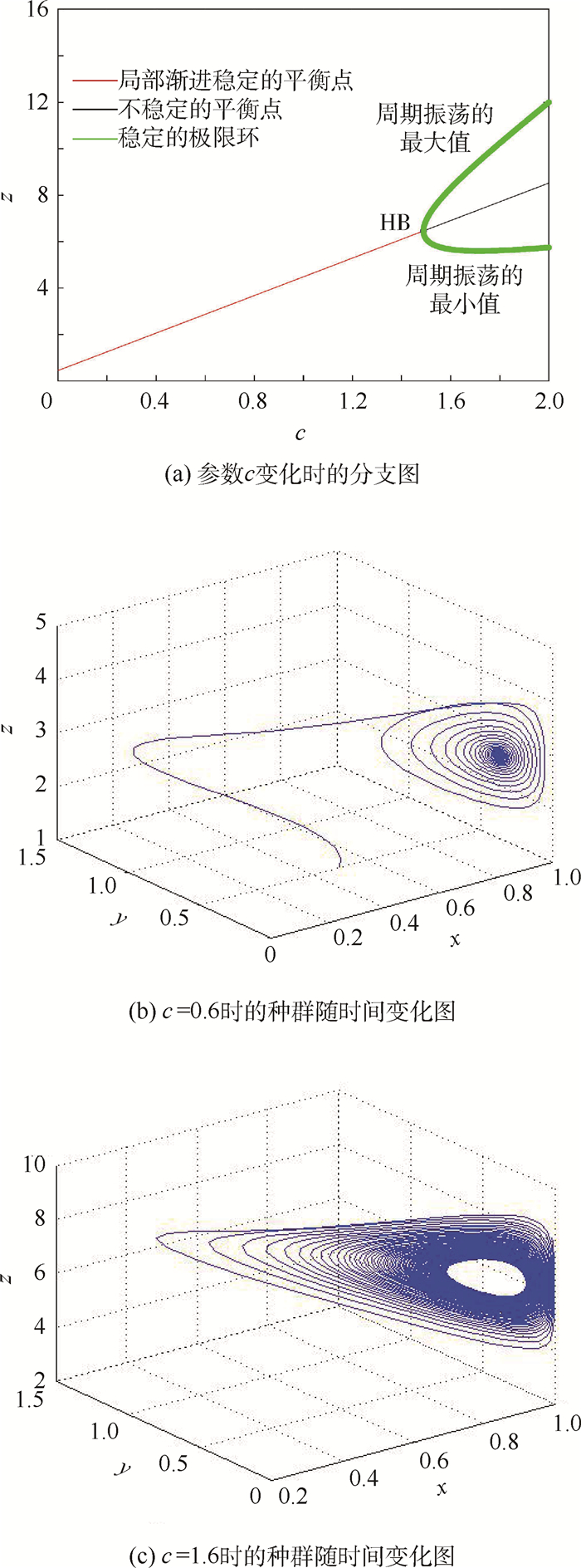
当c < c*时,内部平衡点局部渐进稳定,而当c=c*时,出现Hopf分支。图 3(a)是利用软件XPPAUT绘制出的以c为参数的分支图,其他参数取值为:a1=6, a2=0.2, b1=2, b2=0.05, d1=0.3, d2=0.04,A=0.2。
在c*≈1.5时产生Hopf分支。在此点左侧,内部平衡点局部渐进稳定(图 3(b));在此点右侧,内部平衡点变为不稳定,出现局部渐进稳定的周期解(图 3(c))。
|
| 图 3 c为分支参数时的系统稳定性 Fig. 3 Stability of system with bifurcation parameter c |
选择A作为参数,可以更深入研究食饵选择性对系统稳定性的影响。由于s不是关于A的单调函数,因此改变A的值对系统稳定性的影响更复杂。图 4(a)给出一组参数下的系统分支图,各参数取值为:a1=4, a2=0.5, b1=1, b2=0.5, d1=d2=0.3, c=0.5。

|
| 图 4 A为分支参数时的系统稳定性 Fig. 4 Stability of system with bifurcation parameter A |
从图 4中可以看出,当A较小时,内部平衡点不稳定;A增加到大约0.191 3时出现局部渐进稳定的周期解(图 4(b));A继续增加,当A≈0.198 7时产生Hopf分支(图 4(c)),出现局部渐进稳定的内部平衡点,周期解由稳定变为不稳定;A≈0.262 4时,产生另外一个Hopf分支,其中HB为Hopf分支点;A继续增加到0.4,内部平衡点消失,边界平衡点(x, y, 0)局部渐进稳定(图 4(d))。
4 结论本文根据捕食者对多种食饵的选择性,建立了一个三维食物链系统,推导出种群共存的充分条件以及Hopf分支条件。通过数值仿真,对理论结果进行了验证和补充。
研究结果表明,食饵选择性可能会对系统的稳定性产生关键性影响:
1) 种群对食饵选择性的不同,会引起边界平衡点稳定性的改变。中间捕食者增加对其他可供选择的食饵的捕食比率,有利于其生存。
2) 捕食者对其他食饵的选择性也对系统的3个种群共存有着不可忽略的影响。当选择参数A较小或者对其他食饵的摄食量较多时,则系统中某些种群可能消失;而随着中间捕食者对其他食饵的捕食量的增大,系统中的3个种群将以周期振荡的形式共存于系统或者最终数量达到稳定。
综上所述,食饵的多样性选择对种群的多样性具有促进作用,有利于生态平衡和生态稳定。
| [1] | FREEDMAN H I, WALTMAN P. Mathematical analysis of some three-species food chain models[J]. Mathematical Biosciences, 1977, 33 (3) : 257 –276. |
| [2] | HASTINGS A, POWELL T. Chaos in a three-species food chain[J]. Ecology, 1991, 72 (3) : 896 –903. DOI:10.2307/1940591 |
| [3] | HSU S, HWANG T, KUANG Y. A ratio-dependent food chain model and its applications to biological control[J]. Mathematical Biosciences, 2003, 181 (1) : 55 –83. DOI:10.1016/S0025-5564(02)00127-X |
| [4] | GINOUX J M, ROSSETTO B, JAMET J L. Chaos in a three-dimensional Volterra-Gause model of predator-prey type[J]. International Journal of Bifurcation and Chaos, 2005, 15 (5) : 1689 –1708. DOI:10.1142/S0218127405012934 |
| [5] | PATHAK S, MAITI A, SAMANTA G P. Rich dynamics of a food chain model with Hassell-Varley type functional responses[J]. Applied Mathematics and Computation, 2009, 208 (2) : 303 –317. DOI:10.1016/j.amc.2008.12.015 |
| [6] | GEORGE A K, KOOI P I, BOER M P. Ecological consequences of global bifurcations in some food chain models[J]. Mathematical Biosciences, 2010, 226 (2) : 120 –133. DOI:10.1016/j.mbs.2010.04.005 |
| [7] | STRAUSS S Y. Indirect effects in community ecology: Their definition, study and importance[J]. Trends in Ecological Evolution, 1991, 6 (7) : 206 –210. DOI:10.1016/0169-5347(91)90023-Q |
| [8] | SAHOO B, PORIA S. Diseased prey predator model with general Holling type interactions[J]. Applied Mathematics and Computation, 2014, 226 (1) : 83 –100. |
| [9] | HUXEL G R, MCCANN K. Food web stability: The influence of trophic flows across habitats[J]. American Natualist, 1998, 152 (3) : 460 –469. DOI:10.1086/286182 |
| [10] | HUXEL G R, MCCANN K, POLIS G A. Effects of partitioning allochthonous and autochthonous resources on food web stability[J]. Ecological Research, 2002, 17 (4) : 419 –432. DOI:10.1046/j.1440-1703.2002.00501.x |
| [11] | SRINIVASU P D N, PRASAD B S R V, VENKATESULU M. Biological control through provision of additional food to predators: A theoretical study[J]. Theoretical Population Biology, 2007, 72 (1) : 111 –120. DOI:10.1016/j.tpb.2007.03.011 |
| [12] | SAHOO B.Effects of additional foods to predators on nutrient-consumer-predator food chain model[J/OL].ISRN Biomathematics, 2012.http://dx.doi.org/10.5402/2012/796783. |
| [13] | SAHOO B.Global stability of predator-prey system with alternative prey[J/OL].ISRN biotechnology, 2013.http://dx.doi.org/10.5402/2013/898039. |
| [14] | SAHOO B, PORIA S. Disease control in a food chain model supplying alternative food[J]. Applied Mathematical Modelling, 2013, 37 (8) : 5653 –5663. DOI:10.1016/j.apm.2012.11.017 |
| [15] | SAHOO B, PORIA S. The chaos and control of a food chain model supplying additional food to top-predator[J]. Chaos Solitons & Fractals, 2014, 58 (1) : 52 –64. |



