压电网络复合板(PEMP)由分布在薄板表面(单面或双面)的压电片用电路彼此相连形成的压电网络和薄板复合而成,其与一般压电复合板不同之处在于压电网络的存在,为压电片中汇集的电能在结构中的传播提供了通道。作为一种新型的智能材料复合结构,压电网络复合板在振动噪声控制等领域具有广阔的应用前景。近年来,在基于压电材料的结构系统振动控制研究领域中,大部分研究人员将研究重点放在了压电分支阻尼技术方面[1-4],通过设计不同形式的压电分支电路,如电感电阻谐振型电路和负电容电路等,实现了不同结构的多模态振动控制等目标,并利用相关技术解决了压电分支电路中普遍存在的因电感值过大而难以实现的问题[5-6]。Dell′Isola和Vidoli[7]在1998年提出利用电感、电阻和压电陶瓷元件构造压电网络的思想,并对桁架结构进行减振效果分析;在此基础上,Dell′Isola[8-9]和Park[10]等进一步研究了压电网络对梁结构、板结构等更加复杂的结构系统的振动抑制效果;Wang等[11-12]将这种思想用于旋转周期结构如叶盘结构的减振研究中,发现压电网络可以有效降低结构的局部振动现象,并且在非谐叶盘结构上进行了进一步电路设计,提高了压电网络的鲁棒性;2012年Fan和Li[13]研究了利用压电网络将一些结构部件的振动能量传递到另一些结构部件并对其振动进行抑制;最近,Lossouarn等[14]采用实验手段验证了压电网络对杆和梁的多模态控制效果。以上研究表明,压电网络形式的电路能够充分利用压电材料的正逆压电效应,实现能量的重新分布。2014年李琳和易凯军[15]对压电网络复合板的建模方法、频率特性以及机电耦合特性进行了深入的理论研究;李俊等[16]则研究了压电网络对固支板的多模态振动控制效果。但是以上研究还缺乏实验验证。
本文针对文献[15, 17]的研究结果,通过设计压电网络复合板振动控制实验,验证不同类型压电网络对薄板的振动控制效果,并通过实验说明压电网络复合板的最优电感参数的选取原则,为工程应用提供参考。
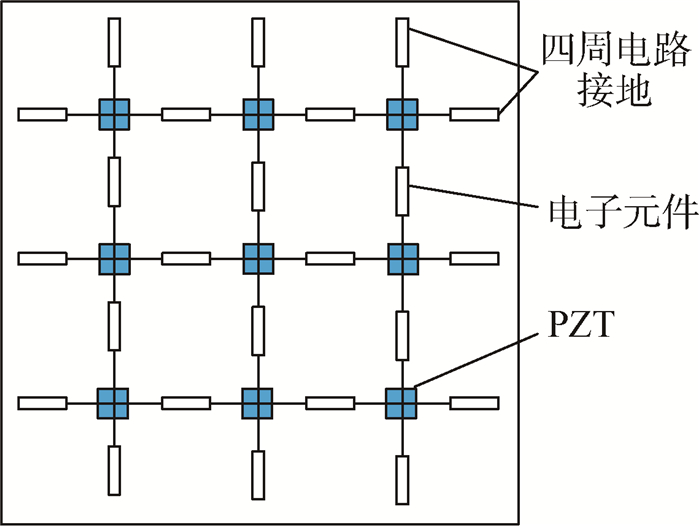
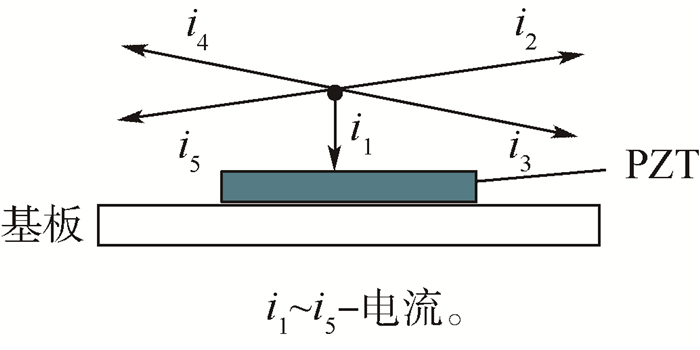
1 压电网络复合板模型及频率响应函数 1.1 机电耦合动力学方程压电网络复合板由图 1所示的压电复合板和压电网络2个部分组成。压电网络将压电复合板上周期分布的压电材料(实为作动器PZT)彼此相连,其特点是连接各相邻压电作动器的电路完全相同;压电网络中压电片上表面与周围压电片上表面(或地)通过电子元件连接。图 2为压电片在电路中的连接方式。
|
| 图 1 压电网络及复合板的连接 Fig. 1 Connection of composite plate with piezoelectric network |
|
| 图 2 压电片的电路连接方式 Fig. 2 Circuit connected way of piezoelectric patch |
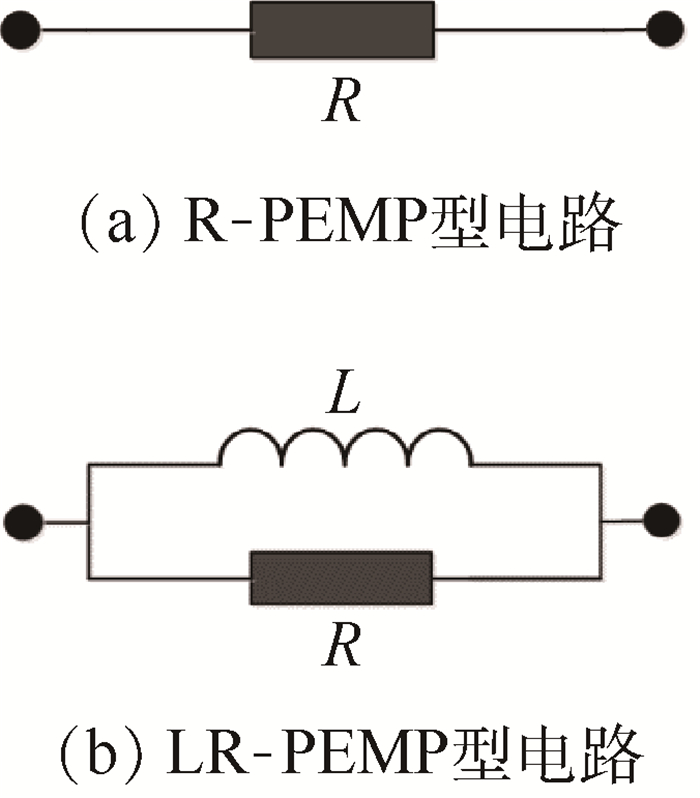
压电网络复合板根据压电片之间电路或电学元件的不同,可以分为图 3所示2种情况,即电阻(R)型压电网络复合板(R-PEMP)和电感(L)电阻(R)并联型压电网络复合板(LR-PEMP)。
|
| 图 3 压电片之间的电路形式 Fig. 3 Circuit patterns between piezoelectric patches |
参照文献[15]中建立压电网络复合板机电耦合动力学方程的过程,可建立压电网络复合板在任意机械激励下的无量纲机电耦合动力学方程:
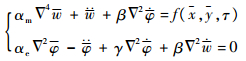
|
(1) |
式中:w为压电复合板的无量纲横向位移; φ为压电网络的无量纲磁通量; αm为与压电复合板刚度相关的系数; αe为与压电网络外接电感和压电片自身的电容相关的系数;β为机电耦合参数,表示压电片与基板的耦合刚度;γ与外接的电阻参数有关;f(x, y, τ)为作用于压电复合板上的无量纲激振力,x、y和τ分别为无量纲空间坐标以及无量纲时间。本文无量纲化过程中使用的特征频率为压电网络复合板的第1阶固有频率
方程式(1)在建立过程中,采用了材料均质化假设和压电网络有限差分方法,该假设成立的条件是板中传播的弯曲波波长远大于元胞的尺寸。本文研究的频率范围符合上述条件。
1.2 方程的求解本文以四边简支板为研究对象,首先给出机械激励下的压电网络复合板的频率响应函数,在此基础上进行实验研究。
压电网络复合板的响应函数和可分别表示为方程式(1)中2个解耦微分方程的特征解函数的线性组合[15],即
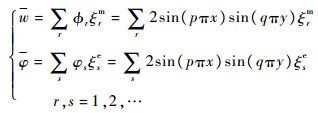
|
(2) |
式中:变量定义参见文献[15]。
将式(2)代入动力学方程式(1),并由特征解函数的正交性可以得到压电网络复合板在外界激励下的第k阶机电耦合动力学方程为
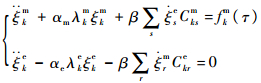
|
(3) |
式中:αmλkm为压电复合板第k阶共振频率的平方; -αeλke为电路第k阶谐振频率的平方;fkm(τ)=∫sϕk f(x, y, τ)ds为模态力; λkm=π4(p2+q2)2;λke=π2(p2+q2);Cksm和Ckre为不同模态间的耦合项,其表达式为
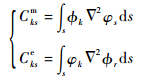
|
(4) |
由特征解函数的正交性可得
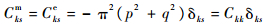
|
(5) |
式中:Ckk为机电耦合系数;δks为狄拉克函数。
即只有当k=s时耦合项Cksm、Ckse才不为零。式(5)表明电路的第k阶模态与板的第k阶模态存在耦合关系,从振动控制的角度来分析,即压电复合板与压电网络的振动模态相同时,压电网络可对压电复合板产生直接影响。
因此,第k阶振动方程为
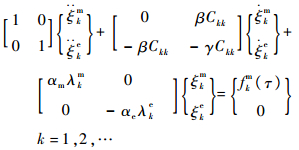
|
(6) |
式(6)为一系列模态解耦的机电耦合方程组。考虑简谐激励时,模态力fmk(τ)亦具有简谐形式:
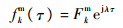
|
(7) |
式中:Fkm为模态力幅值;λ为无量纲频率;j为虚数单位。
此时方程式(6)的解可以表示为
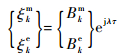
|
(8) |
将式(7)和式(8)代入式(6)可得
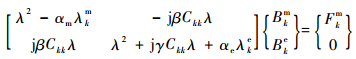
|
(9) |
其复幅值响应为
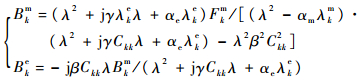
|
(10) |
Bkm的模表示压电网络复合板第k阶机械场频率响应幅值,将求解的式(8)代入式(2)即可求解压电网络复合板在任意频率下的频率响应。由推导过程和式(10)可知,当同阶模态下电路谐振频率与压电复合板共振频率接近时,压电网络能够对薄板进行振动控制。
2 实验装置、测试方法及模拟电感电路 2.1 实验装置实验装置由测试系统和实验件2个部分组成。测试系统由计算机、OROS振动信号分析仪、电压放大器、压电陶瓷激振器、固定支架和加速度传感器及导线等部分组成(如图 4和图 5所示)。计算机通过控制OROS振动信号分析仪产生一组幅值一定的正弦慢扫频电压信号,经过电压放大器放大后驱动粘贴在实验件(即压电网络复合板)表面上的压电陶瓷激振器,进而激励压电网络复合板振动,激励器位置见图 5。利用加速度传感器拾取压电网络复合板上某一点的加速度信号,通过输入输出信号的传递函数即可测得压电网络复合板的传递函数。加速度信号拾取点位置(加速度传感器位置),见图 5。

|
| 图 4 计算机、OROS振动信号分析仪和电压放大器 Fig. 4 Computer, OROS vibration signal analyzer and voltage amplifier |

|
| 图 5 PEMP、激振器和加速度传感器 Fig. 5 PEMP, actuator and acceleration sensors |
实验件(即压电网络复合板)由粘贴了压电片的压电复合板和压电网络2个部分组成,压电复合板见图 5;通过导线将压电片与布置在面包板上的电子元件连接构成压电网络电路,见图 6。由于实验所需的电感值将达几十甚至上百H,会造成电感元件体积过于庞大而难以实现,因此电感元件采用模拟电路实现(2.3节将对其进行详细介绍),模拟电路需要稳压电源为芯片供电。

|
| 图 6 压电网络电路 Fig. 6 Circuits of piezoelectric network |
压电网络复合板中压电材料参数如表 1所示,其中,基板为铝板,尺寸为600 mm×600 mm×2 mm,压电片面积占基板的面积为4%,实验中的电感值为90、133及257 H。
| 材料参数 | 数值 |
| 尺寸/mm | 40×40×0.5 |
| 数量 | 3×3 |
| 密度/(kg·m-3) | 7 800 |
| 介电常数εS33/(10-8F·m-1) | 1.593 |
| 压电系数d31/(10-10C·N-1) | -1.85 |
| 实测电容值/nF | 89 |
2.2 测试方法
实验中,输入信号为电压信号,电压驱动压电片激励压电网络复合板,输出信号为板上一点的加速度信号。系统的传递函数可以表示为
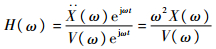
|
(11) |
式中:H(ω)为传递函数;Ẍ(ω)为输出的加速度信号幅值;X(ω)为输出位移信号幅值;V(ω)为输入的电压信号幅值。
实验采用的输入电压激励信号为正弦慢扫描信号,这是一种较为成熟的激励方法,激励信号能量集中、信噪比大、测试精度高,具有较高的频率分辨率。利用该方法进行激励时,首先根据测试结构确定合理的扫频速率,这样测试结果将在一定的容许误差范围内。根据ISO标准规定,正弦扫描通过共振区的最大速率需满足如下条件:
1) 线性扫频速度条件:Smax < 216f r2ξr2 Hz/min,fr和ξr分别为共振频率和模态阻尼。
2) 对数扫描速度条件:Smax < 310f r2ξr2 Oct/min。
实验中使用的激励信号和采样信号的参数如表 2所示,实验中扫频范围为10~410 Hz,本次实验分析的频率范围为10~200 Hz。
| 参数 | 采样频率/Hz | 采样时间/s | 扫频范围/Hz | 扫频速度/(Hz·s-1) |
| 数值 | 1 024 | 655 | 10~410 | 0.605 6 |
2.3 模拟电感电路
压电网络复合板的振动控制需要使用的电感值很大,在实际中较难实现。文献[8]中都通过设计模拟电感电路代替电感元件,以满足实验中的大电感需求。常用的模拟电感电路有2种类型:一种是接地电感电路,另一种是浮地电感电路。
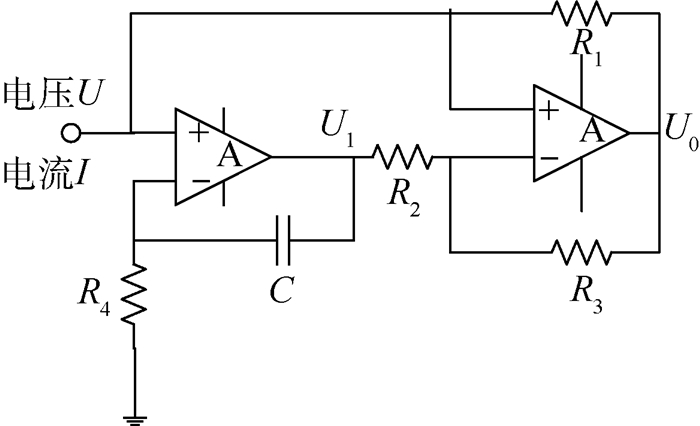
接地电感电路一般采用里奥登电感电路[18]。里奥登电感电路由2个运算放大器、4个电阻(R1~R4)和一个电容元件(C)构成,如图 7所示。
|
| 图 7 里奥登模拟接地电感电路图 Fig. 7 Circuit diagram of Riordan's simulated grounded inductance |
其等效电感值为
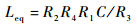
|
(12) |
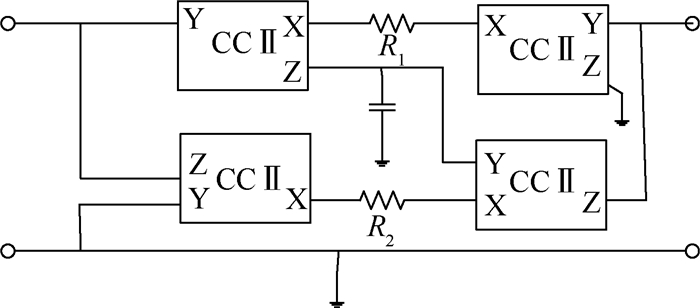
接地电感要求电感电路一端必须接地,这限制了电感电路使用。浮地电感电路可利用第2代电流传输器(CCⅡ+)实现[19],其设计电路图见图 8。
|
| 图 8 模拟的浮地电感电路 Fig. 8 Simulated floating inductive circuit |
电流传输器是一种标准的模拟器件(如图 9所示),电流传输器端口具有以下性质:

|
(13) |
式中:IX、IY和IZ分别为X、Y和Z端的电流; UX、UY和UZ分别为X、Y和Z端的电压。

|
| 图 9 电流传输器CCⅡ Fig. 9 Second generation current conveyors (CCⅡ) |
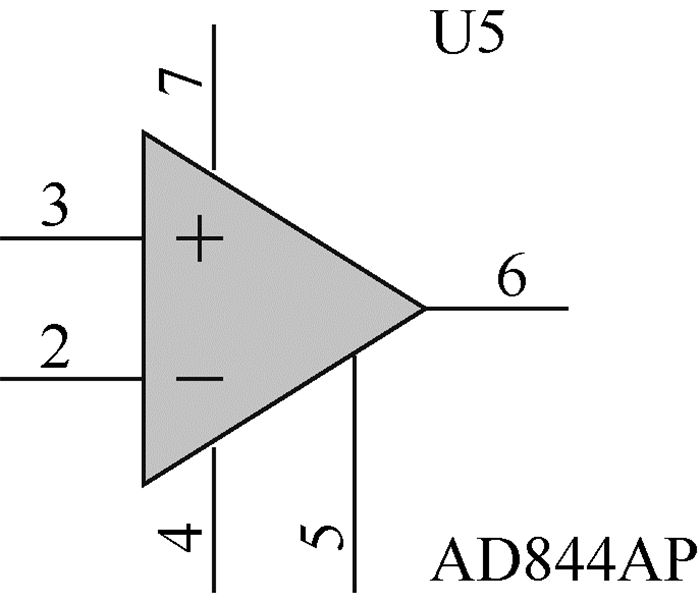
电流传输器CCⅡ+可使用AD844运算放大器代替(见图 10),其等效关系为:2脚等效为X端,3脚等效于Y端,5脚等效于Z端。
|
| 图 10 AD844示意图 Fig. 10 Schematic diagram of AD844 |
浮地电感电路的等效电感值为
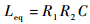
|
(14) |
通过调节电路中的电阻值即可实现对电感值的调节。该模拟电路由于CCⅡ+的X端口存在一寄生电阻,这使得该电路并非纯电感电路,其阻抗可等效为电感与一小电阻的串联。
图 11为制作的模拟接地电感和浮地电感,其芯片需要使用稳压电源进行供电,以保证压电网络电路正常工作。实验时PEMP四周边界电路电感使用接地电感,该电感不存在寄生电阻问题,可以准确调节电感值,且安全可靠;其他电路中电感必须使用浮地电感,使用CCⅡ+实现的浮地电感电路不要求电路参数的对称性,并且其电路的改进型可以实现电感电子可调,更有利于将来的实际应用,但是目前其造价昂贵。

|
| 图 11 模拟电感电路 Fig. 11 Simulated inductive circuit |
实验中模拟电感电路参数如表 3所示,电阻使用电位器,可以实现电感值可调。
| 电感类型 | 参数 | 参数数值 | 等效电感值Leq/H |
| 接地电感 | R1/kΩ | 1 | 0.03R2 |
| R3/kΩ | 1 | ||
| R4/kΩ | 30 | ||
| C/μF | 1 | ||
| 浮地电感 | R3/kΩ | 30 | 0.03R2 |
| C/μF | 1 |
3 实验结果与讨论
实验研究包括测量R-PEMP和LR-PEMP在单点激励下的频率响应曲线,并对两种类型压电网络系统对薄板的振动控制效果进行对比分析。
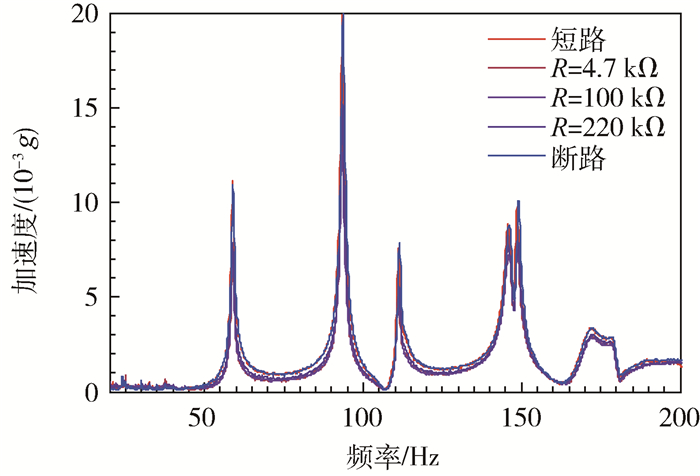
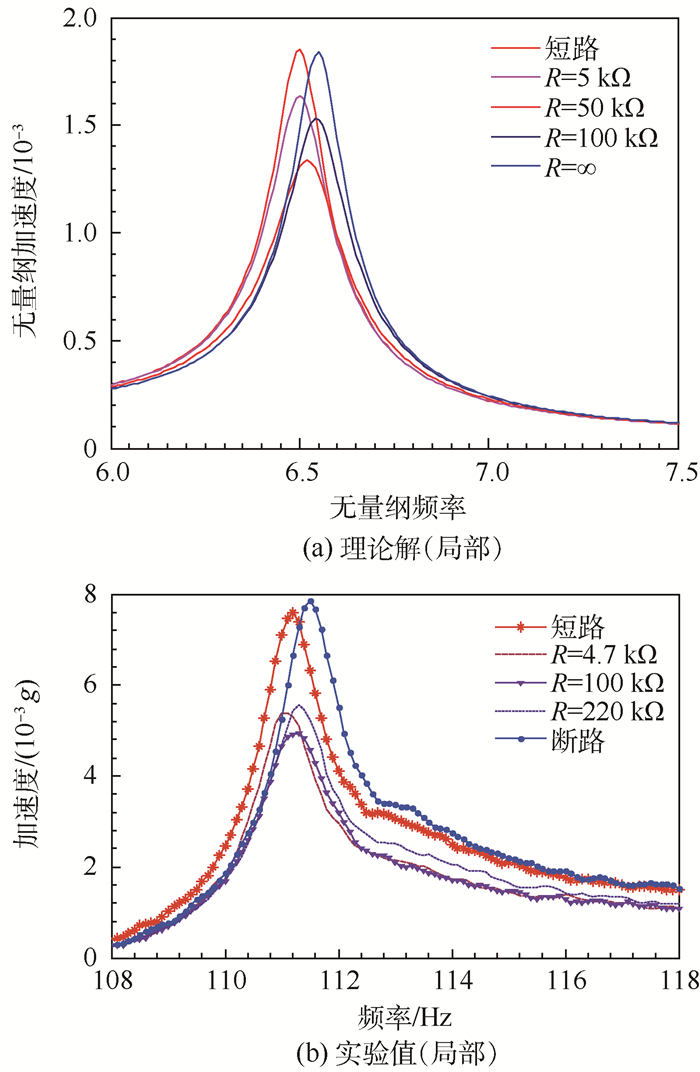
3.1 R-PEMP实验结果对于R-PEMP,分别测量了不同电阻值下R-PEMP的频率响应,并获得了频率响应曲线,如图 12所示。整体上,R-PEMP的振幅随电阻值的变化有一定的降低,但是减振效果有限。图 13为R-PEMP第3个振动峰值频率附近的理论和实测频率响应曲线。理论曲线与实测曲线均表示了R-PEMP随电阻值变化具有相同趋势,即随着电阻增加,R-PEMP共振振幅先减小后增加,即存在最优电阻使R-PEMP减振效果最佳。对于本次实验所采用的实验件,最优电阻值为100 kΩ;开路时R-PEMP的固有频率高于短路时的固有频率(实验中约高出0.4 Hz),表明压电材料的压电效应,使R-PEMP的刚度增加。
|
| 图 12 R-PEMP的频率响应测试曲线 Fig. 12 Test curves of frequency response of R-PEMP |
|
| 图 13 R-PEMP的理论及实验频率响应曲线 Fig. 13 Theoretical and experimental curves of frequency response of R-PEMP |
在对LR-PEMP进行振动抑制效果测试分析前,先对LR-PEMP实验件进行理论分析,以获得使LR-PEMP具有最优控制效果的电感参数。根据初步分析选取电感值为90 H,并联电阻值为1 MΩ。
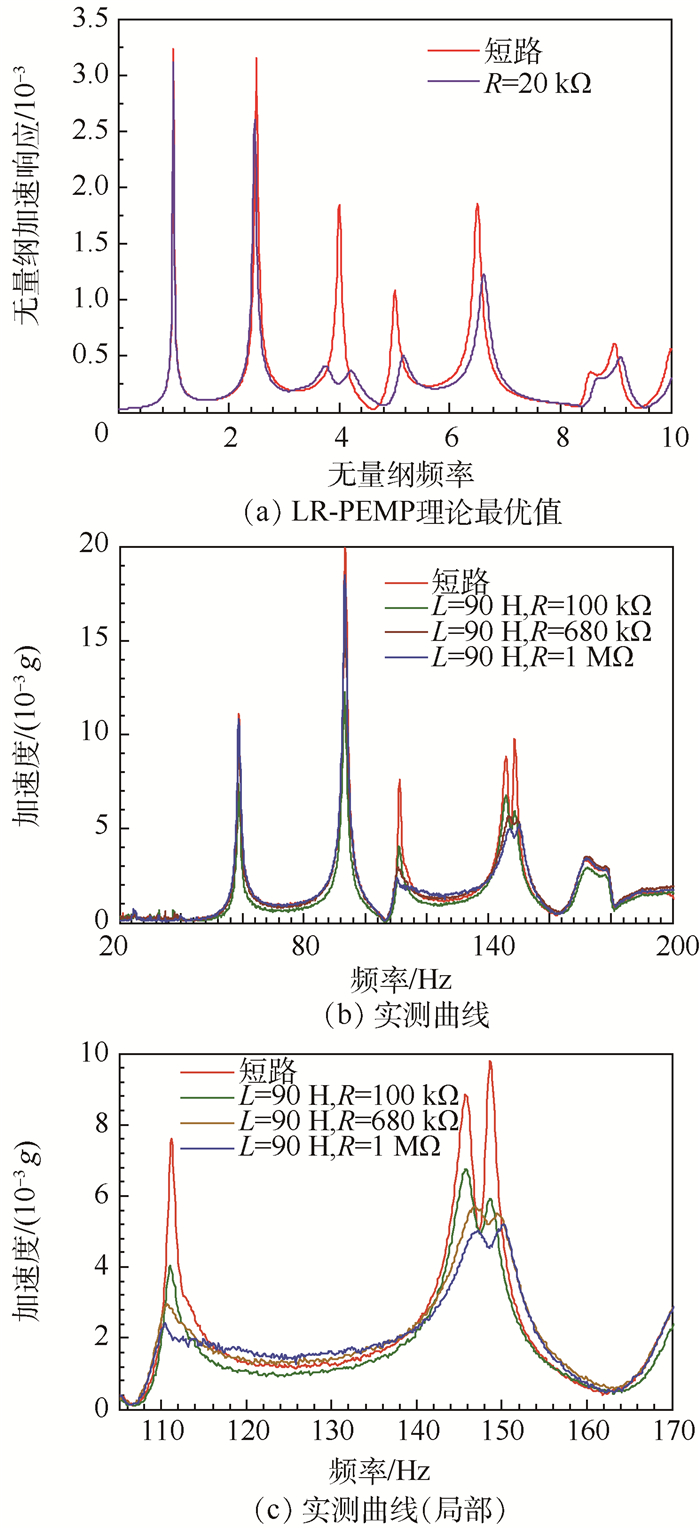
在此电感值下,测量不同电阻值下LR-PEMP的频率响应曲线,测试结果如图 14所示。图 14(a)
|
| 图 14 LR-PEMP的理论与实测频率响应曲线 Fig. 14 Theoretical and measured curves of frequency response of LR-PEMP |
为针对第3阶振动最优参数下LR-PEMP的频率响应的理论解;图 14(b)和图 14(c)为电感值为90 H,不同电阻值下实验测量的频率响应曲线。
理论分析与实测曲线均表明LR-PEMP也具有多模态振动控制效果;由图 14(c)可知减振效果随着电阻值的增大而变好,但不存在最优电阻值,这是由于使用的模拟电感电路中存在一个等效串联电阻的影响,使压电网络电路无法到达最优的控制效果,当等效的串联电阻较大时,还将限制外接电阻阻值的大小。
3.3 振动抑制效果的改善实验结果表明,当电感为90 H时,LR-PEMP频率响应曲线的第3和第4阶共振峰处具有明显振动抑制效果,其中第3阶共振峰处的振动幅值降低75%以上。在第1、2个共振峰处也有减振效果,但是效果明显低于第3、4个共振峰处。由1.2节分析可知,压电复合板与压电网络的振动模态相同时,压电网络可对压电复合板产生直接影响。也就是说振动效果取决于压电网络与压电复合板振动模态的一致性,该一致性包括2个方面:一是固有频率,二是振型。根据以上结论,若要有针对性地提高对第1、2阶共振峰的减振效果,可通过调节压电网络电路中电感值,改变电路的谐振频率,分别使电路相应阶的谐振频率和振型与压电复合板第1阶和第2阶共振频率、振型接近。
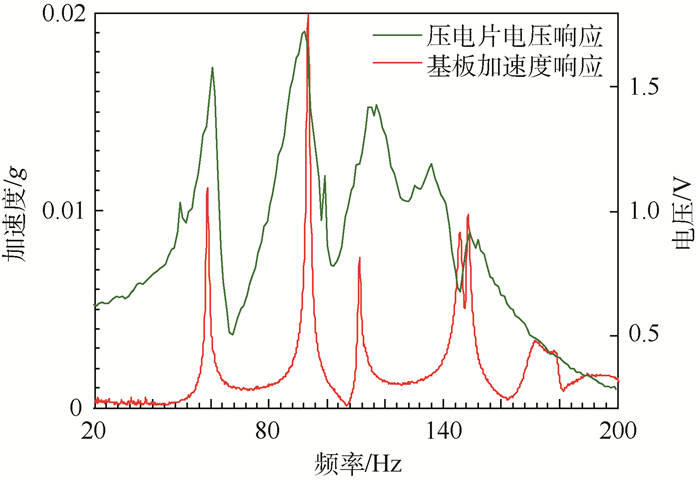
为此先通过理论与实测相结合的方式分别研究了压电复合板和压电网络的模态信息(频率、振型)。通过正弦慢扫频信号激励压电复合板,可以获得压电网络复合板短路时的频率响应曲线, 从该曲线上可提取压电复合板的各阶固有频率信息;通过对电路输入白噪声电压信号,并拾取压电片表面的电压信号,即可测量电路的谐振频率。图 15为电路短路时压电复合板的频率响应曲线和无外接激励下电路的频率响应曲线,其中电感值为90 H,并联电阻值为1 MΩ。该曲线表明压电复合板与压电网络的第1、2阶共振峰对应的频率具有较好的一致性,甚至好于2条曲线第3、4阶共振频率的一致性。为了解释第1、2阶共振峰处的抑振效果不如第3、4阶共振峰的原因,还必须对压电复合板和压电网络的振型进行分析。
|
| 图 15 R-PEMP与压电网络的实验频率响应曲线 Fig. 15 Experimental curves of frequency response of R-PEMP and piezoelectric network |
根据板的振动理论,四边简支(或固支)方板的第1阶振型特征为(1,1),即沿方板的每一周边方向都为一个1/2谐波式变形;第2阶振型为(1,2),即存在一条平行于一个周边的节线;而对实验件的实验模态分析给出的对应第1个共振峰频率的模态振型特征为(1,2)。这意味着压电复合板的第1阶共振在所测得的频率响应曲线上没有显著表现,频率响应曲线上的第1个共振峰实际上对应的是复合板的第2阶振型。分析其原因有可能是由于压电复合板是安装在一个箱体的四边,亦即压电复合薄板一侧是一个封闭的空腔,在密闭空腔气体的压力作用下,其(1, 1)型模态共振幅值很小。
将本节对振型的研究结果及从压电复合板和压电网络频率响应曲线上提取的压电复合板前5阶固有频率和压电网络电路5阶谐振频率示于图 15中。结合图 15和表 4的模态信息不难发现,尽管2条曲线的第1、2阶共振峰十分接近,但它们分属不同的模态。根据1.2节的分析,二者之间没有耦合,压电网络对压电复合板的振动没有直接的影响,因此抑振效果不显著。若要有针对性地提高对第1、2阶共振峰减振效果,需调节压电网络电路中的电感值,使得压电网络振型(1, 2)对应频率尽可能接近压电复合板同阶振型的频率(58 Hz),振型(2, 2)对应频率尽可能接近压电复合板同阶振型频率(93 Hz)。
| 压电复合板模态 | 电路模态 | |||
| 实测频率响应曲线共振峰阶数 | 复合板共振频率/Hz | 振型(实验) | 电路网络谐振频率/Hz | 振型(理论) |
| 1 | 58 | (1, 2) | 61 | (1, 1) |
| 2 | 93 | (2, 2) | 92 | (1, 2) |
| 3 | 111 | 115 | (2, 2) | |
| 4 | 146 | 136 | (2, 3) | |
| 5 | 150 | 152 | (3, 3) | |
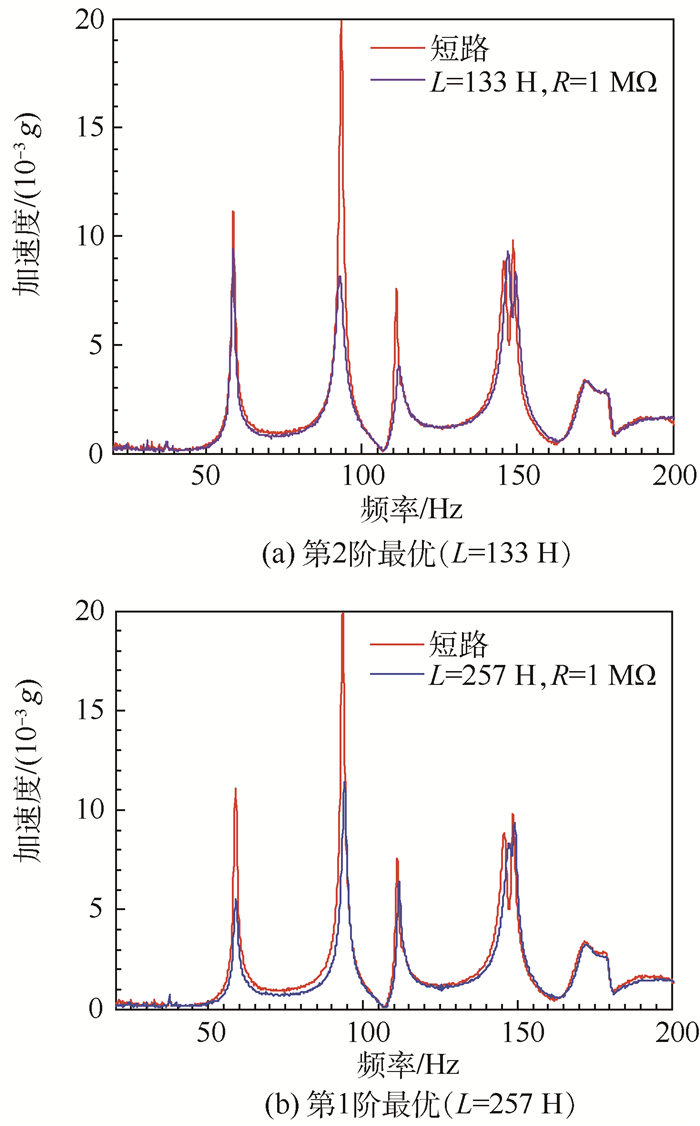
图 16分别给出针对压电复合板频率响应曲线上第1阶和第2阶共振峰最优振动控制下薄板的频率响应曲线,其最优电感值分别为133 H和257 H,相应阶的压电网络谐振频率测量值分别为55 Hz(第1阶)和97 Hz(第2阶),压电网络振幅均降低50%以上。
|
| 图 16 最优参数下的频率响应曲线 Fig. 16 Frequency response curves with optimal parameters |
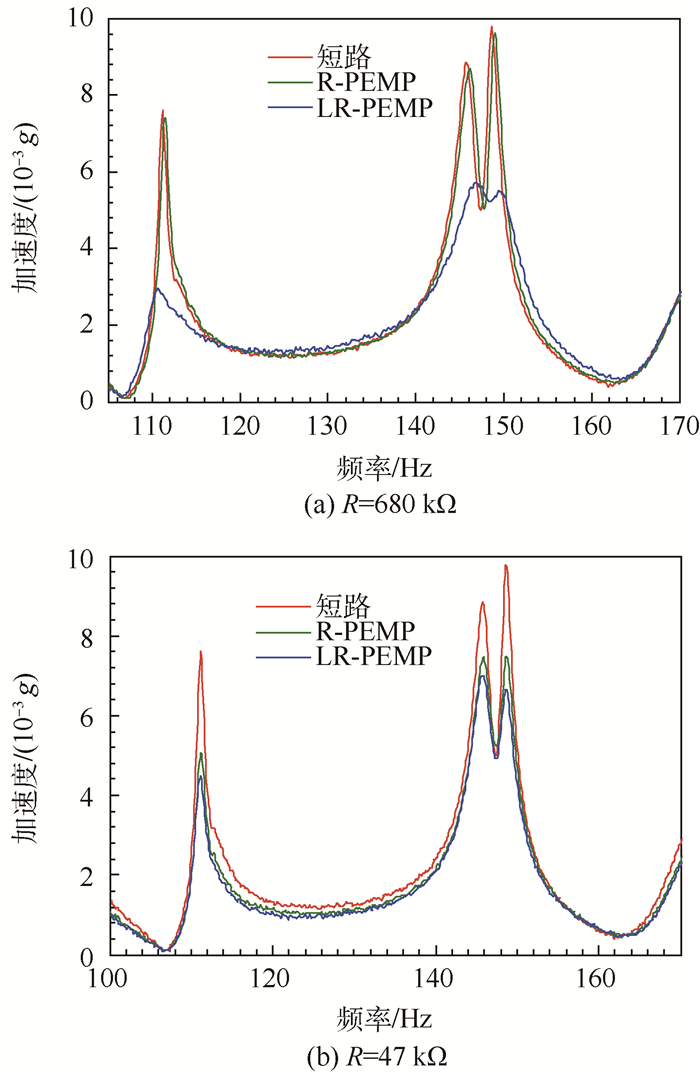
相同电阻值下的R-PEMP和LR-PEMP的频率响应曲线的比较如图 17所示,图 17(a)和图 17(b)分别表示在电阻为680 kΩ和47 kΩ下R-PEMP和LR-PEMP的实测频率响应曲线的比较。
|
| 图 17 LR-PEMP与R-PEMP减振效果的对比 Fig. 17 Comparison of vibration suppression effect between LR-PEMP and R-PEMP |
由图 17(a)可知,相同阻值(R=680 kΩ)下,LR-PEMP和R-PEMP的第3阶振动幅值降低约为60%和2.3%,LR-PEMP减振效果明显优于R-PEMP,这是因为由压电片变形产生的电流值较小,因此在R-PEMP电路中消耗的机械能有限,导致R-PEMP的减振效果较差;当引入电感元件时,形成LR-PEMP,压电网络中电感元件的感抗与压电片自身的容抗在谐振时将会抵消,电路中的电流随之增大,从而增加电阻两端的电压,电路中消耗机械能的功率将增大,故有较好的减振效果。
由图 17(b)可知,当电阻值较小时(R=47 kΩ),LR-PEMP和R-PEMP的第3阶振动幅值降低约为41%和34%,LR-PEMP减振效果与R-PEMP减振效果相当,说明电路中电感作用减小,这是由于与电感并联的电阻减小到一定程度时,相当于将电感两端短路,从而电感失去作用,因此在实际应用中,电感两端并联电阻值不能过小。
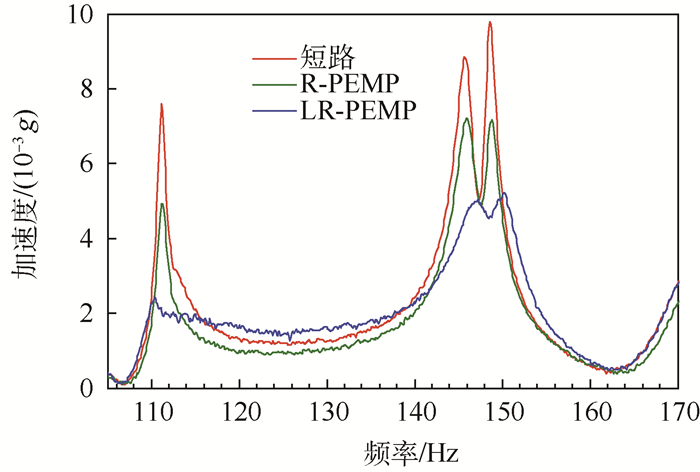
R-PEMP和LR-PEMP取得最优减振效果时的电阻值不同。当2种类型的PEMP的电阻均为最优电阻时(分别为R=100 kΩ和R=1 MΩ),其频率响应曲线如图 18所示,通过比较可知,最优参数下,LR-PEMP的减振效果(75%)也要明显优于R-PEMP(35%)。故LR-PEMP相对于R-PEMP更具有实际应用价值。
|
| 图 18 LR-PEMP和R-PEMP最优参数下的减振效果对比 Fig. 18 Comparison of vibration suppression effect between LR-PEMP and R-PEMP with optimal parameters |
本文采用实测方法对PEMP的振动特性进行研究,通过调节电路参数,对R-PEMP和LR-PEMP的振动控制效果进行研究和实测,得到:
1) 基于均质化的PEMP机电耦合动力学方程能够较好地刻画压电网络PEMP的动力学特性,可以用于分析电学参数对PEMP减振效果的影响规律。
2) R-PEMP具有多模态振动控制效果,对电阻值参数不敏感,但是减振效果有限。
3) LR-PEMP可以针对薄板某阶振动取得最佳振动控制效果,且随着电感的增大,最佳振动控制频带向低频移动;LR-PEMP减振效果要明显优于R-PEMP。
4) LR-PEMP针对某阶共振取得最优振动控制效果的电学参数是使同阶模态下的电路谐振模态信息(包括频率和振型)与压电复合板的同阶模态信息一致的参数。
| [1] | WU S Y.Method for multiple mode shunt damping of structural vibration using a single PZT transducer[C]//Proceedings of SPIE:Smart Structures and Materials:Smart Structures and Intelligent Systems.Bellingham, WA:SPIE, 1998, 3327:159-167. |
| [2] | FLEMING A J, BEHRENS S, MOHEIMANI S O R. Reducing the inductance requirements of piezoelectric shunt damping systems[J]. Smart Materials and Structures, 2003, 12 (3) : 57 –64. |
| [3] | 刘学.基于压电材料的多模态振动控制方法研究[D].北京:北京航空航天大学, 2012. LIU X.Research on multimode vibration control method basedon piezoelectric material[D].Beijing:Beihang University, 2012(in Chinese). http://www.oalib.com/references/16440207 |
| [4] | JI H L, QIU J H, NIE H, et al. Semi-active vibration control of an aircraft panel using synchronized switch damping method[J]. International Journal of Applied Electromagnetics and Mechanics, 2014, 46 (4) : 878 –893. |
| [5] | 张付兴, 阎绍泽. 压电陶瓷片与多种电路机电耦合的阻尼特性[J]. 清华大学学报(自然科学版), 2005, 45 (8) : 1040 –1043. F X, YAN S Z. Damping characteristics of piezoceramics shunted by various types of electrical circuits[J]. Journal of Tsinghua University(Science and Technology), 2005, 45 (8) : 1040 –1043. (in Chinese) |
| [6] | GUYOMAR D, RICHARD C, RICHARD T. Sound wave transmission reduction through a plate using piezoelectric synchronized switch damping technique[J]. Journal of Intelligent Material Systems and Structures, 2008, 19 (7) : 791 –803. |
| [7] | DELL'ISOLA F, VIDOLI S. Damping of bending waves in truss beams by electrical transmission lines with PZT actuators[J]. Archive of Applied Mechanics, 1998, 68 (9) : 626 –636. DOI:10.1007/s004190050192 |
| [8] | DELL'ISOLA F, MAURINI C, PORFIRI M. Passive damping of beam vibrations through distributed electric networks and piezoelectric transducers:Prototype design and experimental validation[J]. Smart Materials and Structures, 2004, 13 (2) : 299 –308. DOI:10.1088/0964-1726/13/2/008 |
| [9] | VIDOLI S, DELL'ISOLA F. Vibration control in plates by uniformly distributed PZT actuators interconnected via electric networks[J]. European Journal of Mechanics-A/Solids, 2001, 20 (3) : 435 –456. DOI:10.1016/S0997-7538(01)01144-5 |
| [10] | PARK C H, INMAN D J. Enhanced piezoelectric shunt design[J]. Shock and Vibration, 2003, 10 (2) : 127 –133. DOI:10.1155/2003/863252 |
| [11] | TANG J, WANG K W. Vibration delocalization of nearly periodicstructures using coupled piezoelectric networks[J]. Journal of Vibration and Acoustics, 2003, 125 (1) : 95 –108. DOI:10.1115/1.1521951 |
| [12] | YU H, WANG K W, ZHANG J. Piezoelectric networking with enhanced eectromechanical coupling for vibration delocalization of mistuned periodic structures-theory and experiment[J]. Journal of Sound and Vibration, 2006, 295 (1-2) : 246 –265. DOI:10.1016/j.jsv.2006.01.006 |
| [13] | FAN Y, LI L.Vibration dissipation characteristics of symmetrical piezoelectric networks with passive branches[C]//ASME Turbo Expo 2012:Turbine Technical Conference and Exposition.New York:ASME, 2012, 7:1263-1273. |
| [14] | LOSSOUARN B, AUCEJO M, DEV J F.Multimodal vibration damping through a periodic array of piezoelectric patches connected to a passive network[C]//Proceedings of SPIE 9431, Active and Passive Smart Structures and Integrated Systems 2015.Bellingham, WA:SPIE, 9431:94311A-1-94311A-14. |
| [15] | 李琳, 易凯军. 压电网络板的机电耦合动力学特性[J]. 北京航空航天大学学报, 2014, 40 (7) : 873 –880. LI L, YI K J. Electromechanical coupled dynamic characteristics of the plate with piezoelectric network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (7) : 873 –880. (in Chinese) |
| [16] | 李琳, 李俊, 易凯军. 基于压电网络的四边固支板多阶共振抑制[J]. 北京航空航天大学学报, 2015, 41 (11) : 1983 –1993. LI L, LI J, YI K J. Multi-mode vibration suppression of clamped plates based on piezoelectric networks[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41 (11) : 1983 –1993. (in Chinese) |
| [17] | 易凯军, 李琳. 压电网络板的振动控制原理与控制效果[J]. 北京航空航天大学学报, 2014, 40 (11) : 1629 –1636. YI K J, LI L. Vibration-controlling mechanism and controlling effectiveness of plate with piezoelectric network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (11) : 1629 –1636. (in Chinese) |
| [18] | RIORDAN R H S. Simulated inductors using differential amplifiers[J]. Electronics Letters, 1967, 3 (2) : 50 –51. DOI:10.1049/el:19670039 |
| [19] | KIRANON W, PAWARANGKOON P. Floating inductance simulation based on current conveyors[J]. Electronics Letters, 1997, 33 (21) : 1748 –1749. DOI:10.1049/el:19971202 |



