2. 北京航空航天大学 航空科学与工程学院, 北京 100083
2. School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
间断Galerkin(DG)方法是由Reed和Hill[1]于1973年为了解决线性输运问题而提出,此后该方法得到了不断发展。20世纪90年代,Cockburn和Shu[2]提出的Runge-Kutta间断Galerkin(RKDG)方法尤其引人注目,在气动力学、水动力学、电磁场以及气动声学等领域的数值模拟中得到了广泛应用。1998年前后,Bassi和Rebay[3]、Cockburn和Shu[4]又将DG方法推广到了黏性流动的计算。近期,Shu[5]对DG方法作了较详细的综述。
DG方法是有限元方法与有限体积方法的结合,在基函数和检验函数的运用方面与有限元方法相似,而在对方程性质的近似方面与有限体积方法更接近,因此有若干优点。首先,与有限元方法一样,间断有限元方法可以方便地提高空间和时间方向的计算精度。在空间上,DG方法可以方便地实施自适应计算,其有2个方面的含义:①对网格单元的自适应加密。DG方法允许单元间出现“悬挂节点”,因此网格加密非常简单。②DG方法允许不同的单元采用不同阶的多项式。这2个方面分别称作h自适应和p自适应。其次,由DG方法形成的常微分方程组,其质量矩阵是分块对角的,甚至可以是单位矩阵,只要在各个单元内选择合适的正交多项式基函数。因为分块对角矩阵求逆相当于各个块矩阵的求逆,所以质量矩阵的求逆计算量极小。分块对角矩阵的逆仍然是分块对角矩阵,所以存储量也极小。最后,间断有限元方法特别适于并行计算。从已有文献可知,间断有限元方法的并行计算效率在80%以上[6]。
与用谱方法求解间断问题会出现Gibbs现象类似,如果解在单元内出现间断,则用高阶多项式作为形函数会导致近似解的振荡。为了获得稳定的近似解,需要引入限制器对解作修正。早期,研究人员开发了一些经典的限制器,如基于minmod函数的TVB限制器[7]、Biswas等[8]的moment限制器、Burbeau等[9]的改进moment限制器、保单调限制器[10]和改进保单调限制器[11]等。之后,类似从差分法中借鉴数值通量概念,间断有限元方法从差分法中借鉴了WENO的思想[12],通过对本单元及相邻若干单元的变量的单元平均作WENO重构,形成了一种新的限制器,得到了高分辨率的结果,成为近年的研究热点。在构造一个合适的WENO限制器前,需要确定哪些单元需要被限制,即识别哪些单元是“问题单元”。早期研究人员按照文献[7]提出的限制器来识别问题单元,即如果某单元需要用到该限制器,则该单元是“问题单元”,否则不是。文献[13]的研究表明,DG方法在单元的出流边界具有很强的超收敛特性,基于此特性构造了一种间断侦测器。在国内,张来平等[14]联合应用该间断侦测器与经典限制器进行了激波捕捉,取得了较好的效果。最近,Zhong和Shu[15]提出了一种简单WENO限制器,取得了较好的间断捕捉效果,而且因为这种限制器只需要用到“问题单元”及其相邻单元的信息,所以编程简单。本文的计算采用这种简单WENO限制器。
1 数学模型考虑Euler方程的守恒形式:

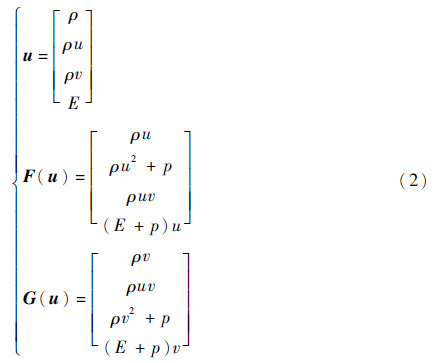


用DG方法对式(1)进行空间离散。设Γh为对区域Ω的一个有限剖分,单元K∈Γh,V(K)为单元K上的局部有限元空间,为Pk(k>0)次多项式的集合。在时间[0,T]内,在如下间断有限元空间中寻找近似解Uh(X,t),这里X=(x,y)。
运用加权余量法,在单元K上用权函数w乘以式(1),并在单元K上积分,有

用近似解Uh(X,t)∈Vh代替式(5)中的精确解U(X,t),用wh∈Vh代替权函数w,利用Green公式有
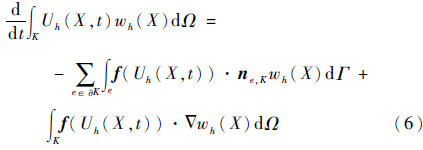
对式(6)用数值积分代替解析积分有
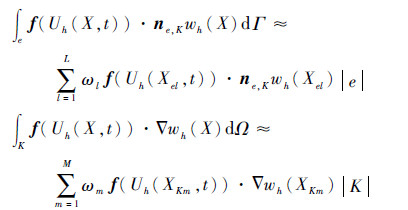
间断有限元方法从差分法中吸收了数值通量的概念,将边界的通量f(Uh(X,t))·ne,K用数值通量函数he,K(X,t)代替,有
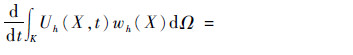
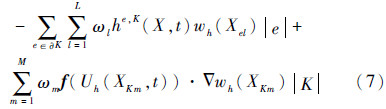
数值通量函数he,K(X,t)在单元边界∂K上的值依赖于近似解在边界两边的值,即由单元K的内部的值Uh(XKint,t)与单元K的外部的值Uh(XKext,t)决定。
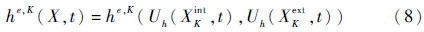
数值通量要求满足相容性、单调性、全局Lipschitz连续性以及守恒性。满足这些条件的数值通量常见类型有Godunov型、Engquist-Osher型、Lax-Friedrichs型、Local Lax-Friedrichs型以及Roe型等。一般来说,Roe型与Local Lax-Friedrichs型计算效果接近,随着逼近多项式阶次的提高,它们对近似解的影响差别很小。对于线性情形,这些数值通量与迎风型数值通量一致;对于非线性问题,因为Godunov型的数值通量产生的人工黏性最小而成为最佳选择。特别地,Local Lax-Friedrichs型数值通量比Godunov型数值通量产生更多的人工黏性。实际计算中,大多采用简化的Lax-Friedrichs型数值通量,而在处理高维双曲系统时,选择Local Lax-Friedrichs型数值通量更为方便。本文计算中均采用Local Lax-Friedrichs型数值通量。
在单元中选取基函数为{Φ1,Φ2,…,ΦJ},这里基函数是关于坐标x和y的多项式,近似解可表示为
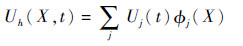
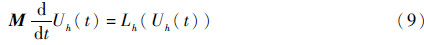
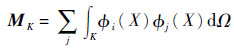 集成的分块对角矩阵。
2.2 时间离散
集成的分块对角矩阵。
2.2 时间离散
式(9)可写为
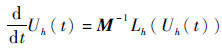

使用如下TVD型显式Runge-Kutta方法求解式(10):

为满足稳定性要求,时间步长取为
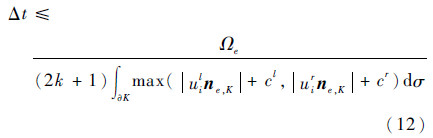
简单WENO限制器由Zhong和Shu[15]提出。简单WENO限制器重构模板小,仅需要用到“问题单元”及其相邻单元的信息,所以特别适合于h自适应计算。这里以三角形单元为例对简单WENO限制器作详细介绍。
设已用某种方法判断出哪些单元为“问题单元”,记“问题单元”的第i条边的外法向为ni=(nix,niy)T,Jacobian矩阵为(f′(u),g′(u))·ni,则该Jacobian矩阵的左右特征向量矩阵为
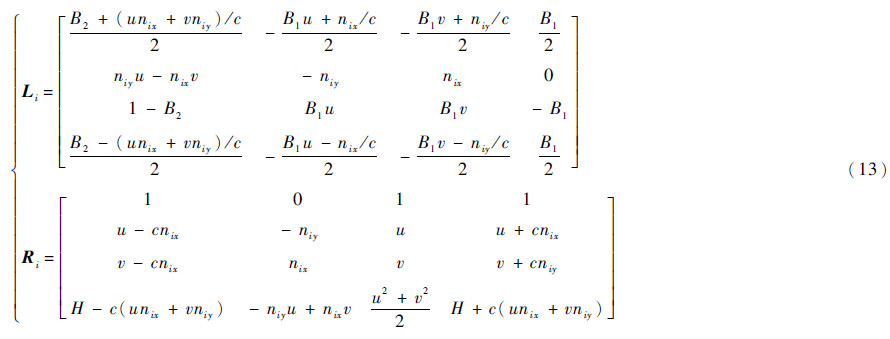
式中: 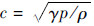 ;B1=(γ-1)/c2;B2=B1(u2+v2)/2;H=(E+p)/ρ。
;B1=(γ-1)/c2;B2=B1(u2+v2)/2;H=(E+p)/ρ。
设需要对“问题单元”Δ0的向量多项式p0(x,y)进行重构,并保持它在单元内的平均值u0(0)(t)。设选择的WENO限制器重构模板为S={Δ0,Δ1,Δ2,Δ3},各个单元上的DG解分别为p0(x,y),p1(x,y),p2(x,y),p3(x,y)。
首先,在单元Δ0的每一个方向ni构造一个新的多项式(p0)inew,分为如下6个步骤:
1) 修改每一个pl为 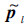 ,使得
,使得 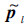 在“问题单元”Δ0上具有与p0(x,y)相同的单元平均。
在“问题单元”Δ0上具有与p0(x,y)相同的单元平均。
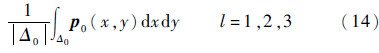
为了方便,记 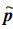 0(x,y)=p0(x,y)。将
0(x,y)=p0(x,y)。将 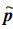 0(x,y),
0(x,y),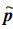 1(x,y),
1(x,y),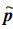 2(x,y),
2(x,y),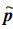 3(x,y)作投影
3(x,y)作投影 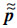 l=Li·
l=Li· 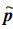 i,l=0,1,2,3,每一个
i,l=0,1,2,3,每一个 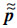 l都是一个k次向量多项式。WENO限制器重构多项式将是4个多项式
l都是一个k次向量多项式。WENO限制器重构多项式将是4个多项式 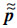 l(x,y)(l=0,1,2,3)的凸组合。
l(x,y)(l=0,1,2,3)的凸组合。
2) 记线性加权系数为ξ0、ξ1、ξ2和ξ3,因为在光滑区域,4个多项式 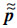 l(x,y)(l=0,1,2,3)都具有k+1阶精度,所以对于加权系数,首先要求满足ξ0+ξ1+ξ2+ξ3=1。另外,通过调节加权系数ξ0、ξ1、ξ2和ξ3来满足解的精度与激波处的本质无振荡的平衡。一般地,取ξ0=0.997,ξ1=ξ2=ξ3=0.001。
l(x,y)(l=0,1,2,3)都具有k+1阶精度,所以对于加权系数,首先要求满足ξ0+ξ1+ξ2+ξ3=1。另外,通过调节加权系数ξ0、ξ1、ξ2和ξ3来满足解的精度与激波处的本质无振荡的平衡。一般地,取ξ0=0.997,ξ1=ξ2=ξ3=0.001。
3) 计算光滑指示子βl,l=0,1,2,3。光滑指示子显式了函数 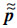 l(x,y)在“问题单元”Δ0上的光滑度。取光滑指示子为
l(x,y)在“问题单元”Δ0上的光滑度。取光滑指示子为
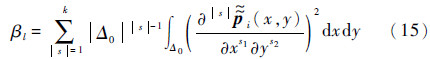
4) 计算基于光滑指示子的非线性加权系数ωl,l=0,1,2,3。
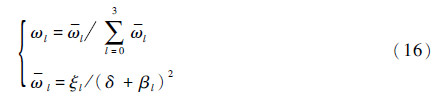
5) 非线性WENO限制器重构多项式( 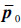 )inew(x,y)定义为
)inew(x,y)定义为 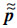 i(x,y)(i=0,1,2,3)的凸组合。
i(x,y)(i=0,1,2,3)的凸组合。
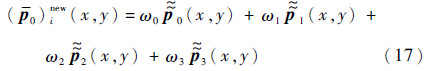
6) 将( 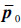 )inew(x,y)投影回物理空间得到
)inew(x,y)投影回物理空间得到
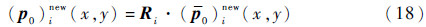
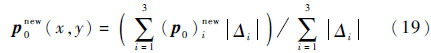
最后用重构多项式p0new(x,y)修改变量u0(l)(t)。
4 基于自适应网格加密的激波捕捉Euler方程是强非线性方程,即使初值连续,其解也可能出现间断。为了捕捉间断,一般会在计算中引入人工黏性,或者用自带耗散效应的格式(如迎风格式、WENO重构等)来抑制振荡。这时,一般只能在1~5个网格内捕捉到激波,计算的分辨率比较低。所以,要提高间断的分辨率,就需要非常细的网格。如果在全流场采用一致的细网格,无疑会增加内存消耗和计算量,也意味着增加了计算时间,降低了计算效率。为了有效解决这个问题,依据解的变化来动态调整网格疏密程度是必要的,这就是通常的h自适应方法。这里简单介绍本文采用的h自适应方法。
4.1 单元间的数据交换由DG方法的原理可知,单元间的信息是通过单元边界交换传递的,具体表现在单元的边界积分的数值通量需要用到相邻单元的边界信息上。对于不做自适应计算的DG程序而言,只需要通过网格节点标号确定相邻单元的单元编号即可。对于h自适应的DG程序,可以通过单元编号的二叉树方法确定相邻单元编号。
本文不采用二叉树方法,而是通过边界高斯积分点的坐标来搜索相邻单元,得到相邻单元的单元编号。这种搜索只在网格细化或粗化后做一次,然后保存该结果。因为需要搜索的点总不在计算域的边界上,而非计算域边界上的单元边总可以修改为直线,所以这种搜索是很方便的。如当单元Ω0某边界高斯积分点的坐标为P(x0,y0)时,首先由点P的坐标判断出其可能属于单元Ω1≠Ω0上,然后若
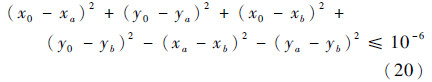
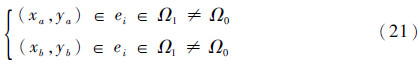
一般而言,h自适应方法根据解的性质来确定局部单元的加密或粗化,即在解急剧变化的地方细化网格,而在解变化较小的地方粗化网格,或者根据解的先验误差估计确定哪些单元细化或粗化。本文旨在提高激波捕捉的分辨率,所以只对“问题单元”进行局部单元加密,对曾是“问题单元”而后来判断不是“问题单元”的单元进行粗化。计算实践表明,这种加密单元的方式是保守的,因为一般情况下根据“问题单元”的判断准则,最终“问题单元”的集合总包含了全部激波附近的单元和和部分非激波附近的单元。
4.3 加密/粗化过程对四边形单元而言,当确定某单元需要加密时,首先将该单元均分为4个子单元,并计算出各子单元上的正交多项式,然后将母单元上变量的表达式映射到子单元上,最后按第4.1节所述方法,得到子单元的各个相邻单元。
当确定某单元需要粗化时,先检验该单元是否可以粗化,因为只有由细化步骤得到的单元才可以粗化,这只需要检验本单元与相邻单元是否可以构成新的直边四边形即可。如果该单元可以粗化,并得到了向量的3个单元,则由这4个单元就可以粗化为1个新的单元。这时,需要计算出新单元上的正交多项式,并将4个单元上的解用最小二乘法投影到新单元上。
5 数值算例 5.1 双马赫反射计算域为[0,4]×[0,1],计算域的底部是固壁。初始条件为一右行的激波,其马赫数为10,始于x=1/6,y=0并与x轴正方向成60°夹角。在底部x∈[0,1/6]的范围内采用激波条件,其他区域采用反射边界条件,计算域的顶部用来流条件。计算网格大小为h=1/100。计算时间取为t=0.2,用3阶精度DG方法计算该问题。图 1为不同时刻的密度等值线。
 |
| 图 1 不同时刻密度等值线 Fig. 1 Density contours at different monents |
从图 1可以看出,使用WENO限制器能清晰地捕捉到流场的间断而无明显的数值振荡产生,能够清晰地捕捉到马赫杆结构。
5.2 NACA0012翼型跨声速绕流来流马赫数为0.8,攻角为1.25°。取来流密度ρ=1.0,速度u=0.8,v=0.0,压力p=1.0/1.4。原始网格及局部加密一次后的网格分别如图 2和图 3所示。原始网格下八节点四边形单元数为5 000,局部网格加密一次后的单元数为5 597。图 4和图 5分别为网格局部加密前后的马赫数等值线。图 6和图 7分别为网格局部加密前后表面压力系数Cp曲线。可以看出,简单WENO限制器能够无波动地捕捉到间断;另外,经过一次局部网格加密后,机翼上下表面激波处马赫数等值线更密集,压力系数曲线斜率更大。
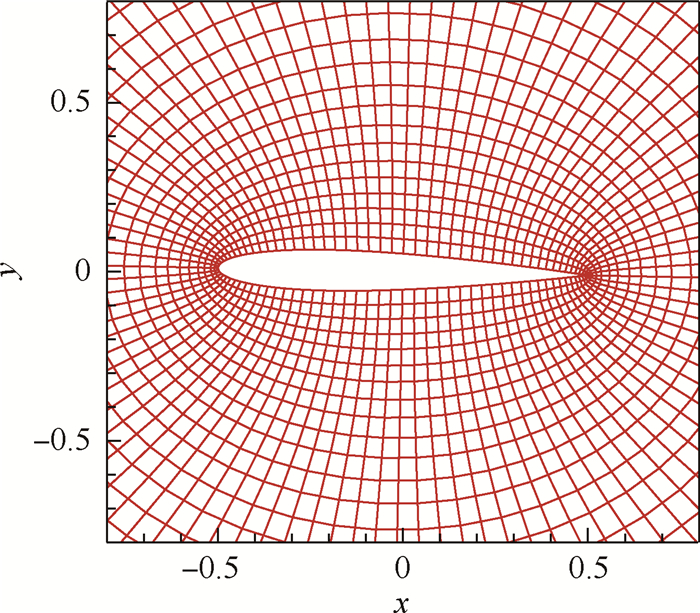 |
| 图 2 NACA0012翼型跨声速绕流原始网格(局部) Fig. 2 Local view of original mesh for transonic NACA0012 flow |
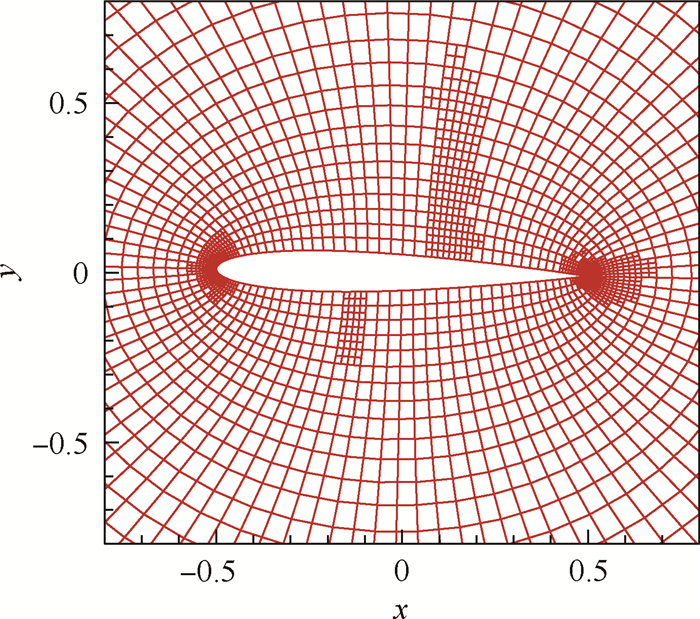 |
| 图 3 NACA0012翼型跨声速绕流局部加密网格 Fig. 3 Local view of adaptive mesh for transonic NACA0012 flow |
 |
| 图 4 NACA0012翼型跨声速绕流原始网格下的 马赫数等值线 Fig. 4 Mach number contours on original mesh for transonic NACA0012 flow |
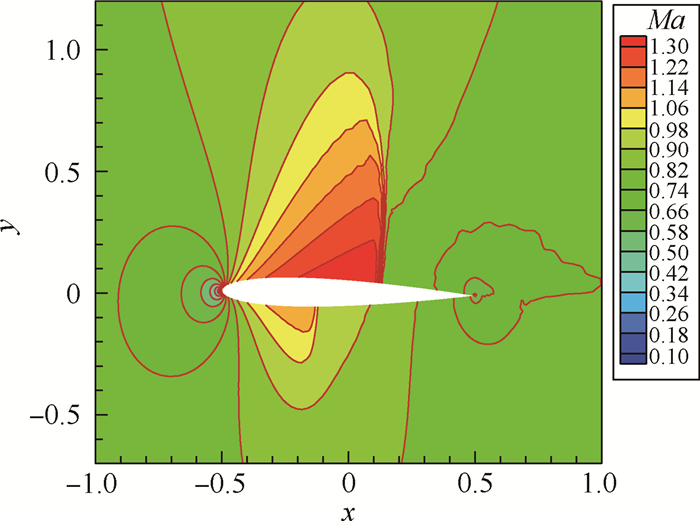 |
| 图 5 NACA0012翼型跨声速绕流网格局部加密后的马赫数等值线 Fig. 5 Mach number contours on adaptive mesh for transonic NACA0012 flow |
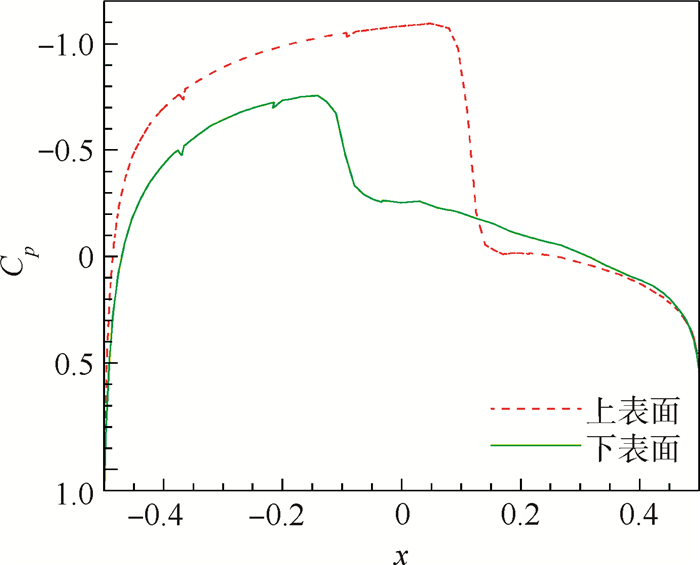 |
| 图 6 NACA0012翼型跨声速绕流原始网格下的表面压力系数分布 Fig. 6 Surface pressure coefficient distribution on original mesh for transonic NACA0012 flow |
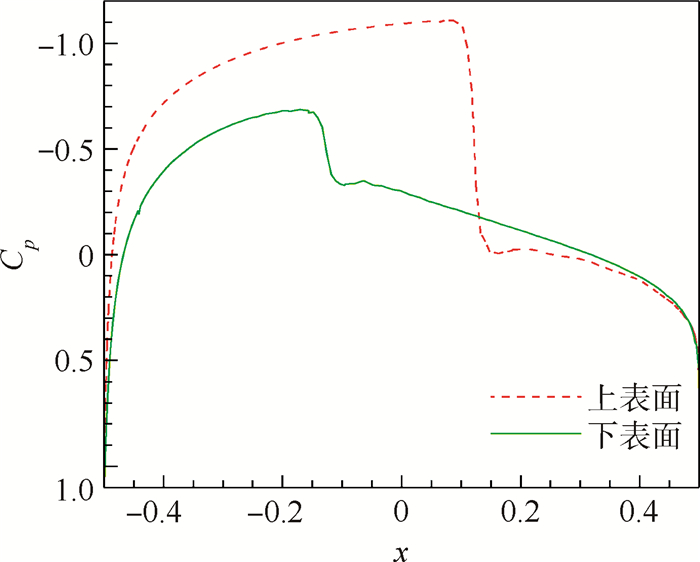 |
| 图 7 NACA0012翼型跨声速绕流网格局部加密后的表面压力系数分布 Fig. 7 Surface pressure coefficient distribution on adaptive mesh for transonic NACA0012 flow |
计算域及原始网格如图 8所示。其中凸起部分为一段圆弧,圆心坐标为(1.5,-3.105),半径为r=3.145。来流马赫数为1.4,取来流密度ρ=1.0,速度u=1.4,v=0.0,压力p=1.0/1.4。计算域的左边为入口边界条件,右边为出口边界条件,上下为反射边界条件。单元采用八节点四边形单元。局部加密一次后的网格如图 9所示。原始网格下单元数为7 500,局部网格加密一次后的单元数为10 476。图 10和图 11分别为网格局部加密前后密度等值线。可以看出,简单WENO限制器能够很好地捕捉到间断;另外,经过一次局部单元加密,密度分辨率有了一定的提高。
 |
| 图 8 4%凸起原始网格 Fig. 8 Full view of original mesh for subsonic flow past 4% bump configuration |
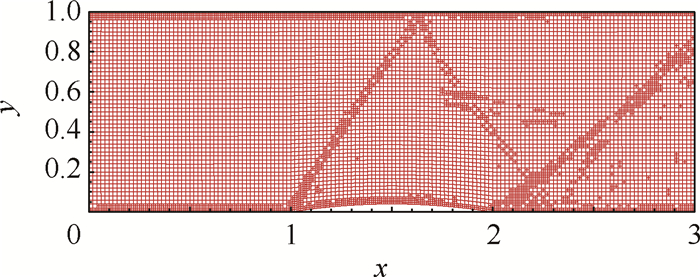 |
| 图 9 4%凸起局部加密网格 Fig. 9 Full view of adaptive mesh for subsonic flow past 4% bump configuration |
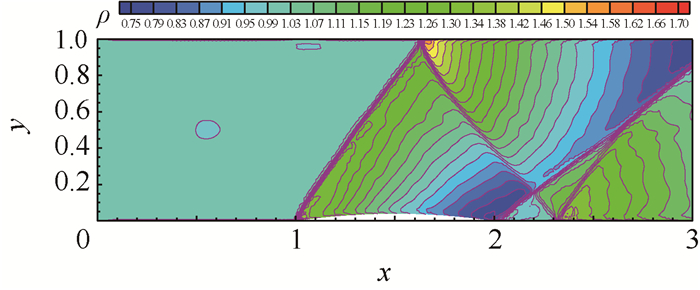 |
| 图 10 4%凸起原始网格下的密度等值线 Fig. 10 Density contours on original mesh for subsonic flow past 4% bump configuration |
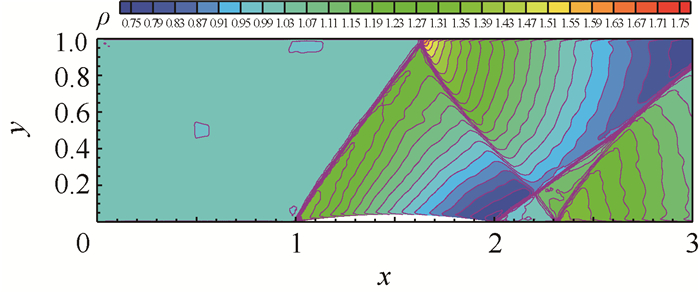 |
| 图 11 4%凸起局部网格加密后的密度等值线 Fig. 11 Density contours on adaptive mesh for subsonic flow past 4% bump configuration |
取2个并行错位的NACA0012翼型超声速绕流,翼型的攻角均为0°,来流马赫数为2.0,取来流密度ρ=1.0,速度u=2.0,v=0.0,压力p=1.0/1.4。本算例同时存在内外双重的流动特征,由于翼型错位和超声速来流,翼型之间的干扰所产生的流场波系比较复杂。计算域为[-6,6.5]×[-6.5,6.5]。计算域的左边为入口边界条件,上、下、右边为远场边界条件,翼型壁面为反射边界条件。单元采用八节点四边形单元。初始局部网格如图 12所示。局部加密一次后的网格如图 13所示。初始网格下单元数为41 237,局部网格加密一次后的单元数为45233。图 14 和图 15分别为网格局部加密前后马赫数等值线。可以看出,下面的翼型未受到干扰,在翼型前缘产生上下对称激波,而上面的激波与下面的翼型产生的激波相交;上面翼型产生的激波的下半支在下面翼型的上表面相交、反射,形成马赫杆结构。另外,简单WENO限制器能够很好地捕捉到间断,经过一次局部单元加密,间断分辨率有了一定的提高。
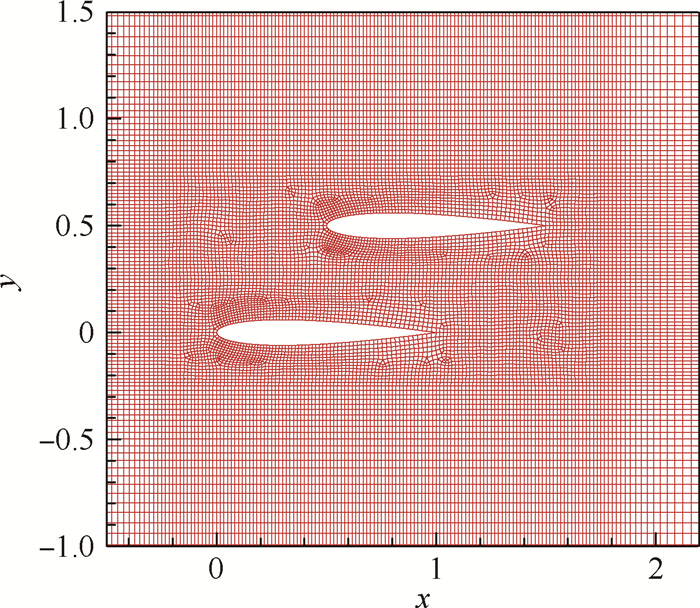 |
| 图 12 2段NACA0012翼型原始网格(局部) Fig. 12 Local view of original mesh for supersonic flow through two staggered NACA0012 airfoils |
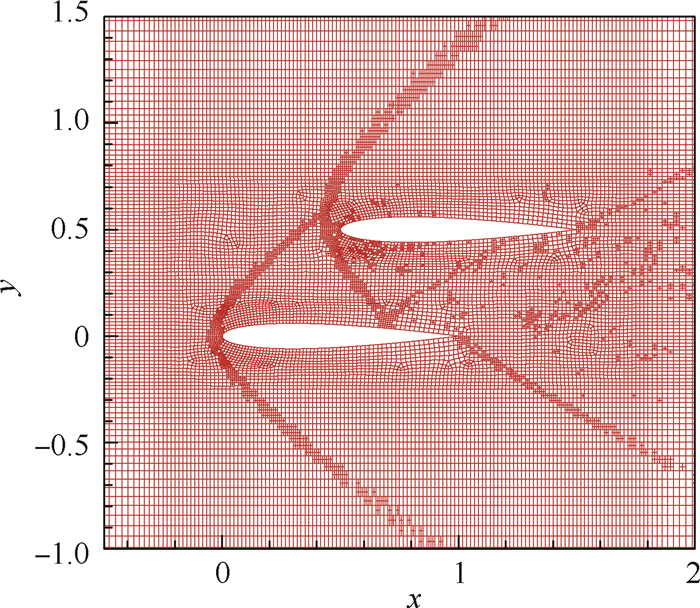 |
| 图 13 2段NACA0012翼型局部加密网格 Fig. 13 Local view of adaptive mesh for supersonic flow through two staggered NACA0012 airfoils |
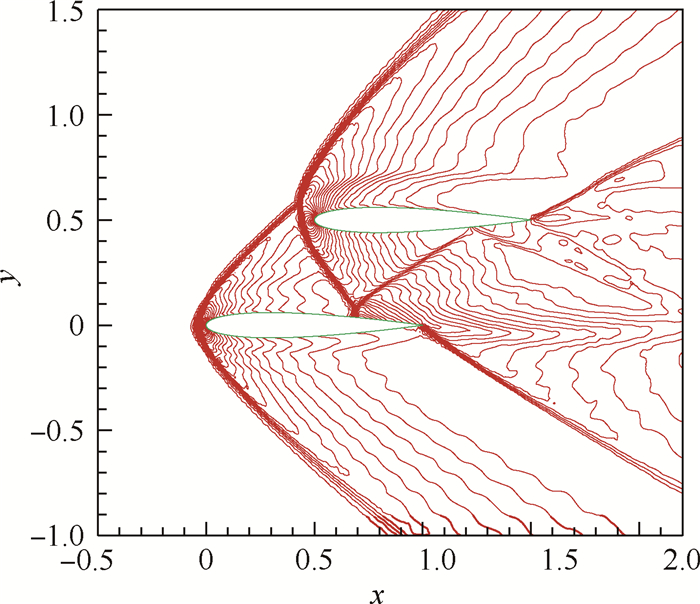 |
| 图 14 2段NACA0012翼型原始网格下的 马赫数等值线 Fig. 14 Mach number contours on original mesh for supersonic flow through two staggered NACA0012 airfoils |
 |
| 图 15 2段NACA0012翼型局部网格加密后的马赫数等值线 Fig. 15 Mach number contours on adaptive mesh for supersonic flow through two staggered NACA0012 airfoils |
本文介绍了间断Galerkin方法、简单WENO限制器的基本原理以及基于自适应网格加密的激波捕捉方法,最后将简单WENO限制器应用到曲边四边形单元上,实现了局部网格加密的自适应计算。通过对若干典型算例进行编程计算,得到如下结论:
1) 简单WENO限制器可以推广应用到曲边四边形单元上。
2) 简单WENO限制器可适用于局部网格加密时具有“悬挂节点”的非结构网格上的激波捕捉。
| [1] | REED W H, HILL T R.Triangular mesh methods for the neutron transport equation:LA-UR-73-479[R].Los Alamos:Scientific Laboratory,1973. |
| [2] | COCKBURN B, SHU C W.The Runge-Kutta discontinuous Galerkin method for conservation laws V:Multidimensional systems[J].Journal of Computational Physics,1998,141(2):199-224. |
| Click to display the text | |
| [3] | BASSI F, REBAY S.A high order accurate discontinuous finite element method for the numerical solution of the compressible Navier Stokes equations[J].Journal of Computational Physics,1997,131(2):267-279. |
| Click to display the text | |
| [4] | COCKBURN B, SHU C W.The local discontinuous Galerkin method for time-dependent convection diffusion systems[J].SIAM Journal on Numerical Analysis,1998,35(6):2440- 2463. |
| Click to display the text | |
| [5] | SHU C W. A brief survey on discontinuous Galerkin methods in computational fluid dynamics[J].力学进展,2013,43(6):541-553. SHU C W.A brief survey on discontinuous Galerkin methods in computational fluid dynamics[J].Advances in Mechanics,2013,43(6):541-553(in Chinese). |
| Click to display the text | |
| [6] | COCKBURN B, KARNIADAKIS G,SHU C W.The development of discontinuous Galerkin methods[M]//COCKBURN B,KARNIADAKIS G,SHU C W.Discontinuous Galerkin methods:Theory,computation and applications.New York:Springer,2000:1-50. |
| [7] | COCKBURN B, SHU C W.TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws II:General framework[J].Mathematics of Computation,1989,52(186):411-435. |
| Click to display the text | |
| [8] | BISWAS R, DEVINE K D,FLAHERTY J.Parallel,adaptive finite element methods for conservation laws[J].Applied Numerical Mathematics,1994,14(s1-3):255-283. |
| Click to display the text | |
| [9] | BURBEAU A, SAGAUT P,BRUNEAU C H.A problem independent limiter for high order Runge Kutta discontinuous Galerkin methods[J].Journal of Computational Physics,2001,169(1): 111-150. |
| Click to display the text | |
| [10] | SURESH A, HUYNH H T.Accurate monotonicity preserving schemes with Runge Kutta time stepping[J].Journal of Computational Physics,1997,136(1):83-99. |
| Click to display the text | |
| [11] | RIDER W J, MARGOLIN L G.Simple modifications of monotonicity preserving limiters[J].Journal of Computational Physics,2001,174(1):473-488. |
| Click to display the text | |
| [12] | QIU J X, SHU C W.Runge-Kutta discontinuous Galerkin method using WENO limiters[J].SIAM Journal on Scientific Computing,2005,26(3):907-929. |
| Click to display the text | |
| [13] | ADJERID S, DEVINE K,FLAHERTY J,et al.A posteriori error estimation for discontinuous Galerkin solutions of hyperbolic problems[J].Computer Methods in Applied Mechanics and Engineering, 2002,191(11-12):1097-1112. |
| Click to display the text | |
| [14] | 张来平,刘伟, 贺立新,等.一种新的间断侦测器及其在DGM中的应用[J].空气动力学学报,2011,29(4):401-406. ZHANG L P,LIU W,HE L X,et al.A shock detection method and applications in DGM for hyperbolic conservation laws on unstructured grids[J].Acta Aerodynamica Sinica,2011,29(4): 401-406(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [15] | ZHONG X, SHU C W.A simple weighted essentially nonoscillatory limiter for Runge-Kutta discontinuous Galerkin methods[J].Journal of Computational Physics,2013,232(1):397-415. |
| Click to display the text |



