重复使用液体火箭发动机(RLRE)可以降低航天发射成本,是未来航天运载器的发展方向之一[1].可用度是可靠性理论的一部分,它也是重复使用系统重要的评价指标,但重复使用液体火箭发动机的复杂性、部件寿命模型的差异等因素使得它的可用度评估工作十分困难,这就使得对重复使用液体火箭发动机可用度的研究工作很少见到.航天飞机主发动机(SSME)作为世界唯一曾可重复使用的液体火箭发动机,对它的研究工作比较多.文献[2]指出SSME的表现并没有预期的那样卓越,对其缺陷进行了分析,并提出增加系统可靠性的措施.Pauschke[3]在系统级、组件级及部件级对它的可靠性进行分析,并给出了部件设计指标和SSME失效故障树.对大型复杂系统的可靠性指标(如可用度)计算,往往假设部件的寿命分布服从指数分布,即部件故障率为常数.同时假定系统部件的修复率也为常数,在此基础上借助故障树分析技术(FTA)进行可靠性指标的计算[4],但这种假设在现实中往往很难成立.因此,为开展液体火箭发动机可重复使用性研究,在理论上寻找具有普遍意义的重复使用液体火箭发动机可用度指标计算方法显得很有必要.
蒙特卡罗(Monte Carlo)数字仿真方法早期在原子核理论的研究中得到了应用,现在它已经被用于包括核工业在内的航空航天、工农医、服务等领域.由于该方法抽样产生的寿命数据具有随机性,使得它可以解决服从任意概率分布的寿命预估问题[5].文献[6]以某液压泵为例利用Monte Carlo方法对复杂可维修系统在完全维修和基本维修下的可用度进行了数字仿真研究,并给出了基本维修条件下系统的最佳预防维修周期.文献[7]对某型自行火炮样车底盘寿命数据进行非参数假设检验,建立了各部件寿命模型,对部件故障优先级进行分类,对自行火炮底盘可靠性、维修性指标进行了仿真计算,该文献中的样车底盘可靠性(广义可靠性)分析思路值得系统可重复使用性研究者借鉴.
本文以SSME高压液氢涡轮泵(HPFTP)为例,结合已有故障统计资料,提出符合威布尔(Weibull)寿命分布要求的HPFTP工作时间数据,并进行非参数Kolmogorov-Simirnov(K-S)检验.利用Monte Carlo仿真对HPFTP的预防维修周期内的可用度进行了计算分析.
1 重复使用系统可用度计算模型 1.1 可用度与可靠性、维修性的关系与可靠度表征系统在规定的时间和规定的条件下完成任务的概率[4]有所不同,可用度表征的是系统完成任务的可用程度,是一种综合可靠性和维修性的量.显然可用度的定性定量研究对于可重复使用系统而言显得更加重要.可用度A与可靠性和维修性的关系公式为
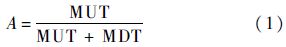
可以看出,可用度是系统可工作时间占总寿命时间(MUT+MDT)的百分比,是对系统的可用程度的定量表述.它比可靠性指标更能反映系统可重复使用的特征.可用度最大说明系统得到了最大程度的利用,为此,将系统最佳可用度定义为系统可用度最大时的取值.
1.2 预防维修周期内系统状态的定性描述可重复使用系统不同于一次性使用系统,如美国的航天飞机作为可重复使用航天运载器侧重的是系统的广义可靠度,即不仅考虑航天飞机完成一次任务的可靠性,而且重视其维修性和完成多次任务的可靠性;而一次性使用的系统则更加关心系统完成一次任务的可靠性.与一次性使用系统相比,可重复使用系统存在着“使用—维修—再使用—再维修—…—报废”这样一个过程和预防维修周期、系统随机故障时间、故障排除时间等的不同概念.预防维修周期T是规定系统累计工作T时间后不论系统发生故障与否都要对系统进行检查维修的时间周期.
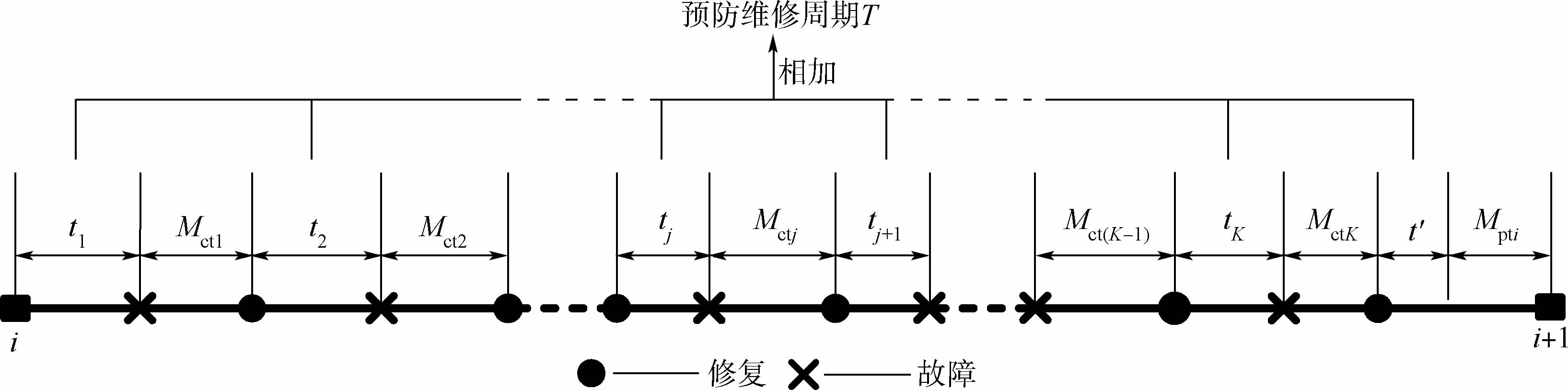
图 1为第i次预防维修周期内可维修液体火箭发动机故障发生与修复的情形.图 1中,tj为系统第i次预防维修周期内系统第j-1次修复后到第j次故障发生前的工作时间;Mctj为系统第j次故障发生后的事后维修时间(为方便表述,这里将故障检测和维修等待等时间均作为维修时间的组成部分,即从发动机发生故障到修复这段不能工作时间都视作维修时间);Mpti为第i次预防维修周期对应的预防维修时间(达到预防维修周期后对系统进行预防维修的时间);K为系统第i次预防维修周期内发生故障的总次数;t′为最后一次故障(第K次)修复后,系统重新开始工作至预防维修周期的时间(t′>0).
|
| 图 1 预防维修周期内可维修液体火箭发动机系统的状态 Fig. 1 States of reusable liquid rocket engine system within preventive maintenance time |
令t为在第i次预防维修周期中系统的累计工作时间,则有如下情形:
1) 若在一个预防维修周期内,系统无故障发生,则在t=T时,进行预防维修.
2) 若在一个预防维修周期内,如图 1所示发生K次故障,每次故障后进行事后维修,则存在:
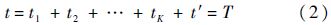
本小节是对修理型事后维修系统的描述.工程中更加关心的问题是在给定的预防维修周期内,如何获得系统的稳态可用度,以及系统是否存在一个最佳的预防维修周期(可用度最大时的预防维修周期).
1.3 基本修复数学模型的建立为了求解第1.2节所描述状态下液体火箭发动机的可用度和最佳预防维修周期,本节参考文献[6]建立液体火箭发动机在基本修复下可用度计算的数学模型.
当液体火箭发动机发生故障后,对其进行维修之后是不可能完好如初的.对于重复使用的发动机,其实际情况更加复杂,本文依据基本修复(即不完全修复)模型来进行分析,即认为修理后的故障率(任意时刻尚未发生故障的液体火箭发动机单位时间内故障发生的概率)与修理前相同.假设第1次发生故障前发动机系统的工作时间为t1(t1=t1),在基本修复条件下按如下方法可以获得第2次故障前系统的总工作时间t2.
以λ表示新坐标系下发动机的故障率,λ表示旧坐标系下发动机的故障率,则发动机在t1时刻发生第1次故障,经基本修复之后,它的故障率λ保持故障前水平λ,即
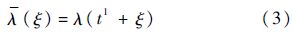
由可靠性理论知,故障率λ(t)与可靠度函数R(t)之间的关系为
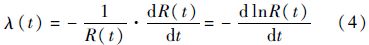
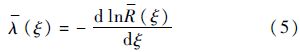
结合式(3)~式(5),并考虑$\frac{dt}{d\xi }=1$,积分可得
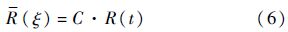
又因发动机在ξ=0时刚刚修复,因此其可靠度应为1,即有R(ξ=0)=1,式(6)可以改写成:
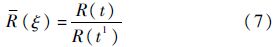
又由可靠度函数与失效分布函数的关系R(t)=1-F(t),可得
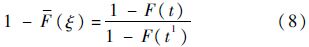
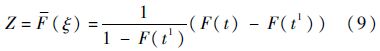
设第1次故障发生时刻失效概率值为Z0,第2次发生故障对应的失效概率值为Z1,则t1=F-1(Z0),结合式(9)可以得到:
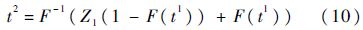
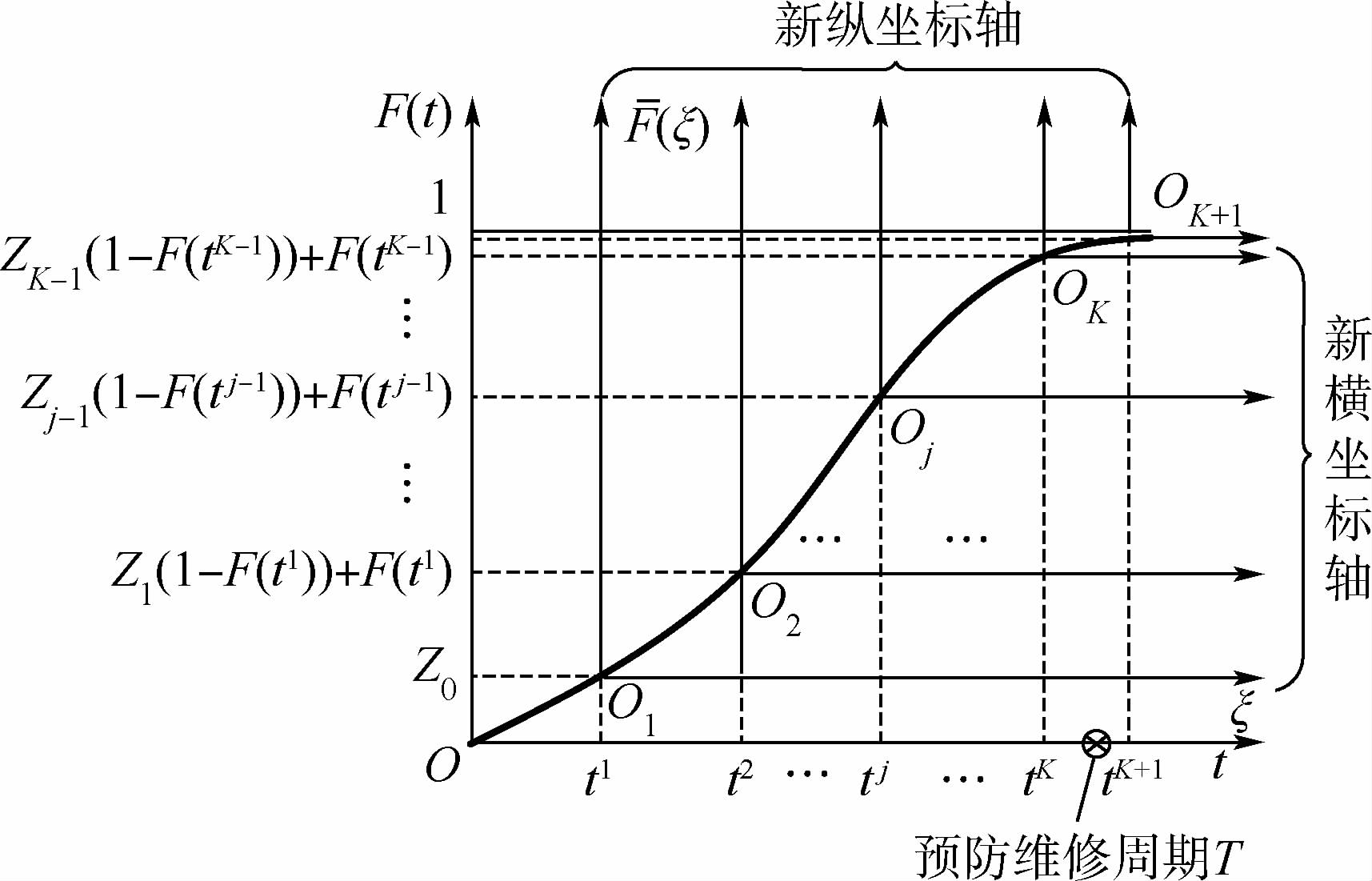
依次类推可以求出基本修复条件下的故障发生时间:
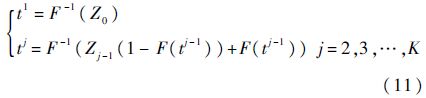
|
| 图 2 基本修复下失效分布函数F(t)随时间的变化 Fig. 2 Changes of failure distribution function F(t) over time under incomplete maintenance |
寿命概率分布模型以对数指数分布和威布尔分布最为常见.本文假设液体火箭发动机的失效分布,即故障前的工作时间概率分布模型服从两参数的威布尔分布,该模型数学表达式为
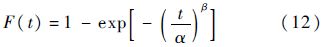
式(11)和式(12)便组成了在基本修复条件下重复使用液体火箭发动机持续工作时间的数学模型,据此可以对液体火箭发动机的工作时间进行数字模拟.注意tj表示系统第j次故障前总的工作时间,tj与tj关系为tj=tj-tj-1(j=2,3,…,K).
下面将通过非参数的K-S假设检验说明威布尔分布对液体火箭发动机的适用性,并给出分布参数的预估值.
1.4 液体火箭发动机失效分布的非参数检验重复使用液体火箭发动机所积累的时间数据往往是地面试车试验中发动机持续工作时间的数据,这些数据与重复使用液体火箭发动机任务时间(如SSME单次任务时间大约500s)和寿命(如SSME设计要求工作55次)是有区别的.但鉴于液体火箭发动机安全性要求很高,而且实际的飞行时间数据又很难获得,本文研究提出如下理由可以认为充分利用地面试验数据来确定重复使用液体火箭发动机预防维修周期是可行的:
1) 地面试验数据是持续工作时间数据,它们往往大于重复使用液体火箭发动机的单次任务时间,这一点通过表 1也可看出,这就表明利用这些数据确定预防维修周期是理论可行的.
工作时间tj/s | 故障数 | 区间概率值 | 分布函数值F(tj) | 代表随机数取值范围 | |
| 1100* | 1 | 0.024 | 0.024 | 0.000~0.023 | |
| 2000 | 1 | 0.024 | 0.048 | 0.024~0.047 | |
| 2846* | 1 | 0.024 | 0.072 | 0.048~0.071 | |
| 4000 | 1 | 0.024 | 0.096 | 0.072~0.095 | |
| 5000* | 2 | 0.048 | 0.144 | 0.096~0.143 | |
| 6000 | 3 | 0.071 | 0.215 | 0.144~0.216 | |
| 7000 | 2 | 0.048 | 0.263 | 0.215~0.262 | |
| 8018* | 2 | 0.048 | 0.311 | 0.263~0.310 | |
| 9000 | 3 | 0.071 | 0.382 | 0.311~0.381 | |
| 10000 | 2 | 0.048 | 0.430 | 0.382~0.429 | |
| 11000* | 3 | 0.071 | 0.501 | 0.430~0.500 | |
| 12000 | 2 | 0.048 | 0.549 | 0.501~0.548 | |
| 13000 | 3 | 0.071 | 0.620 | 0.549~0.619 | |
| 14000 | 2 | 0.048 | 0.668 | 0.620~0.667 | |
| 15000 | 3 | 0.071 | 0.739 | 0.668~0.738 | |
| 16000 | 1 | 0.024 | 0.763 | 0.739~0.762 | |
| 17000 | 2 | 0.048 | 0.811 | 0.763~0.810 | |
| 18000 | 1 | 0.024 | 0.835 | 0.811~0.834 | |
| 19000 | 3 | 0.071 | 0.906 | 0.835~0.905 | |
| 20000 | 2 | 0.048 | 0.954 | 0.906~0.953 | |
| 21000 | 1 | 0.023 | 0.977 | 0.954~0.976 | |
| 22000* | 1 | 0.023 | 1.000 | 0.977~1.000 | |
| 注:第1和第2列中带*的数字取自文献[9],故障总次数42次取自文献[8],其他数据根据HPFTP故障情况假设得到.威布尔分布非参数检验只需用到第1和第2列数据,第3~5列的计算数据为第2节工作时间抽样所用,方便起见,此处一并列出. | |||||
2) 地面试验中出现的故障数据在发动机实际工作中是不允许出现的,即发动机在到达这些时间数据时应不可以有故障发生,否则很可能造成机毁人亡,所以在这些数据前应采取预防维修措施,这就表明利用这些数据确定预防维修周期是合理的.
3) 地面试车后,发动机经简单维修后可以继续工作或故障后不可修,这表明利用这些地面试车数据确定预防维修周期是保守的和安全的.
通过以上分析可知:①地面试车数据与寿命数据具有近似的性质,是一种特殊的寿命数据,它应服从寿命概率分布模型;②利用这些数据确定液体火箭发动机预防维修周期是合理的、保守安全的,这对于合理安排维修资源、提前排除故障是可行的.
不失一般性,本文以SSME HPFTP的持续工作时间数据为例,对其所服从的概率分布模型进行分析,步骤为:
1) 假设HFPTP故障发生前的总工作时间服从式(12)所表达的两参数威布尔分布.
2) 根据总结的HPFTP持续工作时间数据对威布尔分布参数进行预估.
3) 利用非参数K-S检验对所得的持续工作时间模型进行检验.
根据已有数据:HPFTP的FMOF/Phase II、BLOCK I和BLOCK IIA三个技术升级阶段共发生42次故障[8];HPFTP BLOCK II验证阶段试车故障数据参见文献[9].本文依据现有资料摘录或假设或计算得到其故障前的工作时间概率分布如表 1所示,且认为每次故障都可修(能修和值得修).
现根据假设的HPFTP持续工作时间服从的威布尔分布,对表 1中数据进行非参数的K-S假设检验.首先采用最小二乘法利用式(13)和式(14)对威布尔分布的参数进行估算[10]:
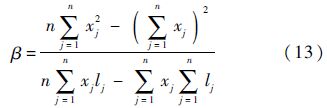
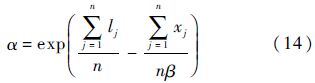
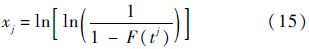

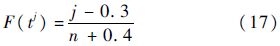
由式(13)~式(17)可以算得HPFTP故障前工作时间所服从的威布尔分布参数:α=13449,β=1.864.
在得知故障前工作时间分布的情况下,采用K-S检验法对假设的模型进行了非参数检验,K-S检验结果:理论结果与经验值的最大距离d_max=0.0818,在置信度ε=0.05下D(42,0.05)=0.2099,又由于所采用的威布尔分布参数是用最小二乘法估算得到的,所以临界值应取4×D(42,0.20)=0.6604.显然d_max<D(42,0.20),也就是说表 1中HPFTP的数据的确服从威布尔分布.
1.5 基本修复条件下系统预防维修时间内工作时间的数字仿真抽样算法利用Monte Carlo随机抽样方法,根据基本修复条件下系统故障发生时间的关系式(11),得出基本修复条件下重复使用液体火箭发动机在给定预防维修周期内工作时间的数字仿真抽样算法,其步骤为:
1) 生成随机数.平均分布随机数采用乘同余法产生,其公式为
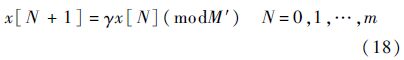
2) 统计系统试验或实际工作中故障发生的时间,按照从小到大的顺序制成系统工作时间概率分布表,以便通过式(11)抽取系统累积工作时间.
3) 给定系统预防维修周期T(由经验或其他计算方法得来),由式(11)中Z0与第1次发生故障的工作时间的关系,利用步骤2)中的系统工作时间概率分布表抽取与Z0对应的系统工作时间t1,若t1≥T则停止该次抽样,计系统工作时间为t1;若t1<T,则将Z0记为η1继续进行步骤4).
4) 第j次的系统工作时间的代表随机数为
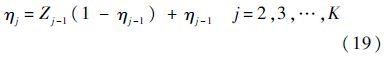
5) 根据步骤2)产生的系统工作时间概率分布表和式(11)(即在系统表 1中查找与ηj对应的工作时间,也即由式(11)所表达的概率分布求逆计算工作时间)抽取ηj所在概率区间(即代表随机数,如表 1中凡落在区间[0.072,-0.095)中所有的随机数的集合即为工作时间等于4000s的代表随机数)的tj+1(j=1,2,…,K),重复步骤4)直到tj+1大于预防维修周期T,停止抽样.
6) 系统每次故障间隔时间为
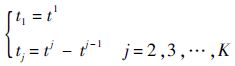
按照第1.5节的方法,根据系统的试验、使用资料,在最小故障时间和最大故障时间之间选取N个时间点进行仿真,在每个时间点进行M次运行,在第i次运行时,只要满足不等式tK+1≥T,则第i次运行结束.在预防维修周期[0,T]内,可求出:
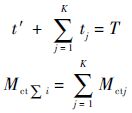
最后,可用度为
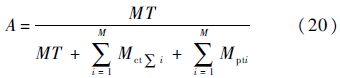
这样就得到预防维修周期T内系统的平均可用度,当运行完所有时间点时就得到了系统在不同预防维修周期内的平均可用度.
2 重复使用HPFTP可用度仿真实例HPFTP是SSME寿命最短的组件,文献[12]指出其能满足11次(5500s)飞行要求,文献[13]指出其能满足34次(17000s)飞行要求(HPFTP一直不断升级更新,不同时期的飞行次数有所差异),故本节以HPFTP为例进行实例分析.需要指出的是,由文献[13]知SSME的寿命(55次飞行任务)是以大修(更换或维修主要零部件)前的时间来定义的,而又通过文献[14]得知HPFTP的寿命也是用大修前的时间定义的,故HPFTP的寿命是大修前的工作时间,这是它与一般产品相区别的典型特点.而HPFTP的寿命则是由多个预防维修周期组成的.大多数文献资料是对SSME或HPFTP的寿命进行研究,而针对HPFTP寿命相关的故障、维修信息进行数字仿真研究的文献还未见到.由第1.4节的分析可知,研究HPFTP的预防维修周期,对于合理分配维修资源,降低风险是有参考价值的.本节用上文提到的数字仿真技术对HPFTP预防维修周期进行实例研究.结合HPFTP一定的试验和使用数据计算其最大可用度,确定对应该可用度的最佳预防维修周期,并结合HPFTP实际工作次数来说明计算方法的合理性.HPFTP持续工作时间数据资料已在表 1中给出,HPFTP维修时间的资料比较有限,结合文献[15],给出假设的预防维修时间概率分布如表 2和事后维修时间概率分布如表 3(表 2和表 3中第1列数据根据文献[15]SSME维修时间估算得来).
| 预防维修时间/s | 区间概率值 | 分布函数值 | 代表随机数取值范围 |
| 2500 | 0.06 | 0.06 | 0.00~0.05 |
| 5000 | 0.15 | 0.21 | 0.06~0.20 |
| 7500 | 0.18 | 0.39 | 0.21~0.38 |
| 10000 | 0.17 | 0.56 | 0.39~0.55 |
| 12500 | 0.20 | 0.76 | 0.56~0.75 |
| 15000 | 0.16 | 0.92 | 0.76~0.91 |
| 17500 | 0.04 | 0.96 | 0.92~0.95 |
| 20000 | 0.03 | 0.99 | 0.96~0.98 |
| 22500 | 0.01 | 1.00 | 0.99~1.00 |
| 注:预防维修时间随机发生,根据定性的判断(过低和过高的预防维修时间发生较少)给出各预防维修时间的区间概率值,即第2列数据,然后计算相应的分布函数值和代表随机数范围. | |||
| 事后维修时间/s | 区间概率值 | 分布函数值 | 代表随机数取值范围 |
| 36000 | 0.16 | 0.16 | 0.00~0.15 |
| 43200 | 0.23 | 0.39 | 0.16~0.38 |
| 50400 | 0.14 | 0.53 | 0.39~0.52 |
| 57600 | 0.18 | 0.71 | 0.53~0.70 |
| 64800 | 0.16 | 0.87 | 0.71~0.86 |
| 72000 | 0.09 | 0.96 | 0.87~0.95 |
| 79200 | 0.04 | 1.00 | 0.96~1.00 |
| 注:事后维修时间随机发生,根据定性的判断(过低和过高的事后维修时间发生较少)给出各事后维修时间的区间概率值,即第2列数据,然后计算相应的分布函数值和代表随机数范围.表2与表3维修时间数据以文献[15]中的维修数据为参照给出. | |||
表 2和表 3是在航天飞机使用历史数据的基础上推断计算而来的,因很难给出与实际情况完全一致的概率分布类型,故本文假设其任意维修类型都是随机发生的(因为故障发生类型随机性很大,所以对应的维修类型也有很大随机性),通过后文的计算结果可以看出数据与假设是较合理的.
对HPFTP进行26个预防维修周期的仿真(预防维修周期区间个数的划分根据所研究问题来确定.比如HPFTP每次工作大约500s,预防维修周期通常取其整数倍,以在发生故障前排除安全隐患),分别取预防维修周期为1500s,2000s,2600s,3400s,…,10000s,11500s,12700s,…,21400s和22000s(理论上预防维修周期可任意选取,文中为了说明方法的任意性取了如2600s之类的非500s整数倍数据,不影响结果的分析说明).每个预防维修周期进行40次运行(即求和指标中M=40),然后计算平均可用度(由统计学知运行次数越多越接近真实值).现仅列出T=10000s时的运行仿真计算结果,如表 4所示.
| 序号 | t1/s | Mct1/s | t2/s | Mct2/s | t3/s | t′/s | T/s | $\sum\limits_{j=1}^{k}{{{M}_{ctj}}}$/s | Mpti/s |
| 1 | 5000 | 57600 | 9000 | 43200 | 18000 | 1000 | 10000 | 100800 | 12500 |
| 2 | 6000 | 43200 | 15000 | — | — | 4000 | 10000 | 43200 | 10000 |
| 3 | 9000 | 36000 | 18000 | — | — | 1000 | 10000 | 36000 | 15000 |
| | | | | | | | | | |
| 39 | 2846 | 79200 | 14000 | — | — | 7154 | 10000 | 79200 | 20000 |
| 40 | 17000 | — | — | — | — | 0 | 10000 | 17000 | 15000 |
| 合计 | 420151217 | 648000 | 460000 | ||||||
| 注:“…”—省略掉的部分抽样数据;“—”—仿真结果已满足条件而不再抽样. | |||||||||
由表 4可以看出,当T=10000s时:
总的工作时间MT=420151217s
总的事后维修时间$\sum\limits_{i=1}^{M}{{{M}_{ct\sum{i}}}}$=648000s
总的预防维修时间$\sum\limits_{i=1}^{M}{{{M}_{pti}}}$=460000s
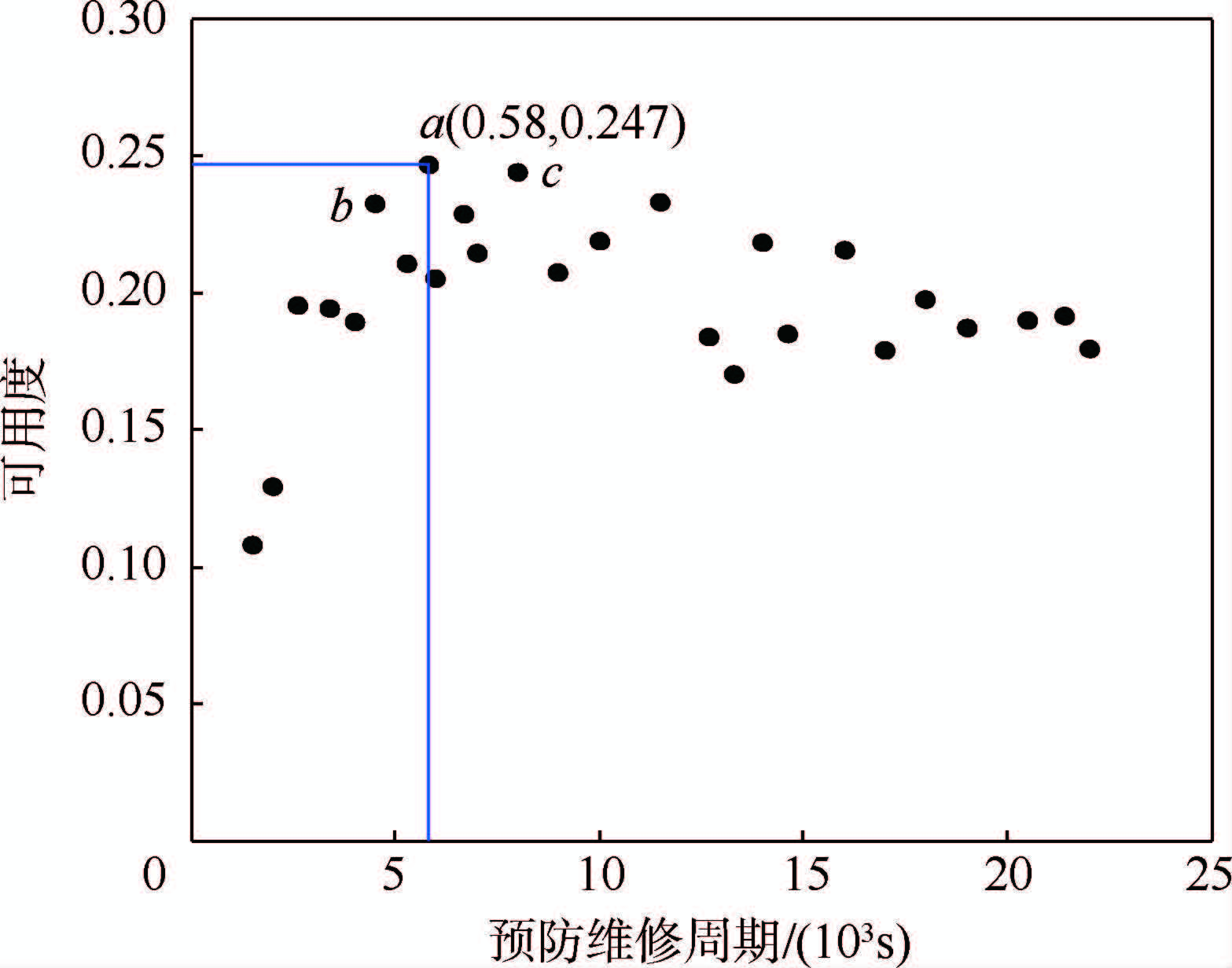
利用式(20)计算得到HPFTP在预防维修周期10000s时的可用度为0.22.同样可以计算得到其它预防维修周期内HPFTP的可用度,以此做出HPFTP的可用度-预防维修周期关系图,如图 3所示.
|
| 图 3 HPFTP可用度-预防维修周期关系 Fig. 3 HPFTP availability-preventive maintenance time relationship |
通过图 3可以看出:①在基本修复条件下,HPFTP的可用度首先随着预防维修周期的增大而增大,但当预防维修周期超过5800s时,其可用度开始下降.这主要是由于预防维修时间太长涡轮泵部件的“老化”而引起故障频发,增加了涡轮泵事后维修时间引起的,所以HPFTP存在最佳预防维修周期.其可用度的最大值是0.247,此时对应的预防维修周期是5800s,即HPFTP的最佳预防维修周期为5800s;②HPFTP的可用度比较低,这主要是因为作为航天用的涡轮泵,其严格的工作要求、安全性和经济性等因素使得它工作时间短、停机时间长引起的;③图 3中的点a,b和c的可用度相差不大,在实际的工程应用中不能肯定a而否定b和c,应根据实际需要选择适合自己的最佳预防维修周期.需要指出的是:如第1.2节所述文中最佳可用度是指最大可用度,这一最佳可用度对应的预防维修周期为最佳预防维修周期.但实际的最佳预防维修周期并不一定取在可用度最大的位置,真正的最佳预防维修周期是需要利用多学科优化、协调分配来确定的,故本文所采用的最佳预防维修周期的概念需要引起注意.
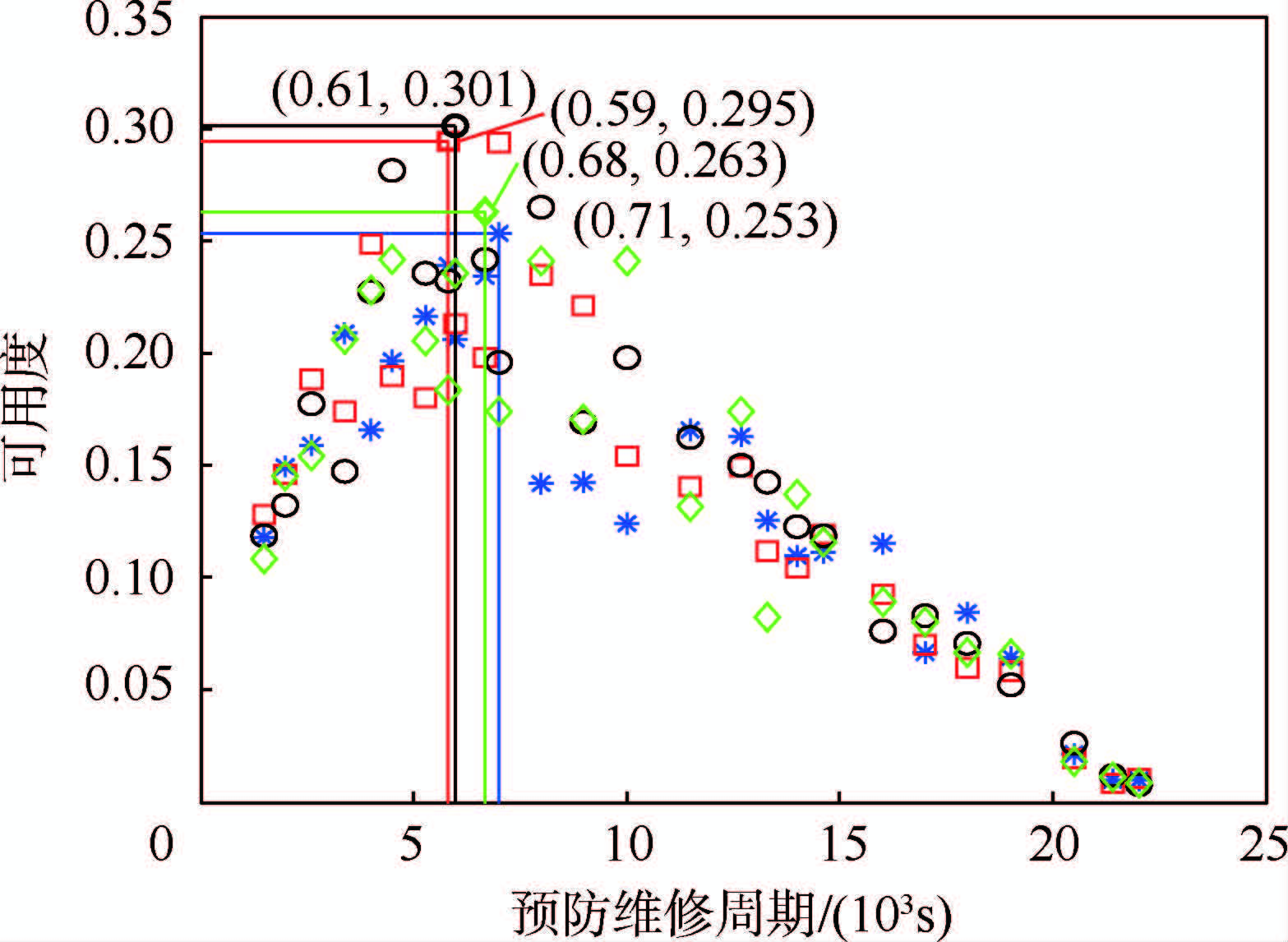
图 4为4次HPFTP可用度数字仿真结果的规律分布图.由图 4可以看出,4次运行中HPFTP的最佳可用度在0.253~0.301,对应的最佳预防维修周期在5900~7100s,这是由于仿真的随机性引起的,符合现实规律.应当多次计算求得平均最佳可用度和平均最佳预防维修周期,但计算次数的选取不是任意的,计算次数与预防维修周期存在一定的关系,如图 5所示.
|
| 图 4 HPFTP可用度-预防维修周期规律分布 Fig. 4 HPFTP availability-preventive maintenance time distribution |
|
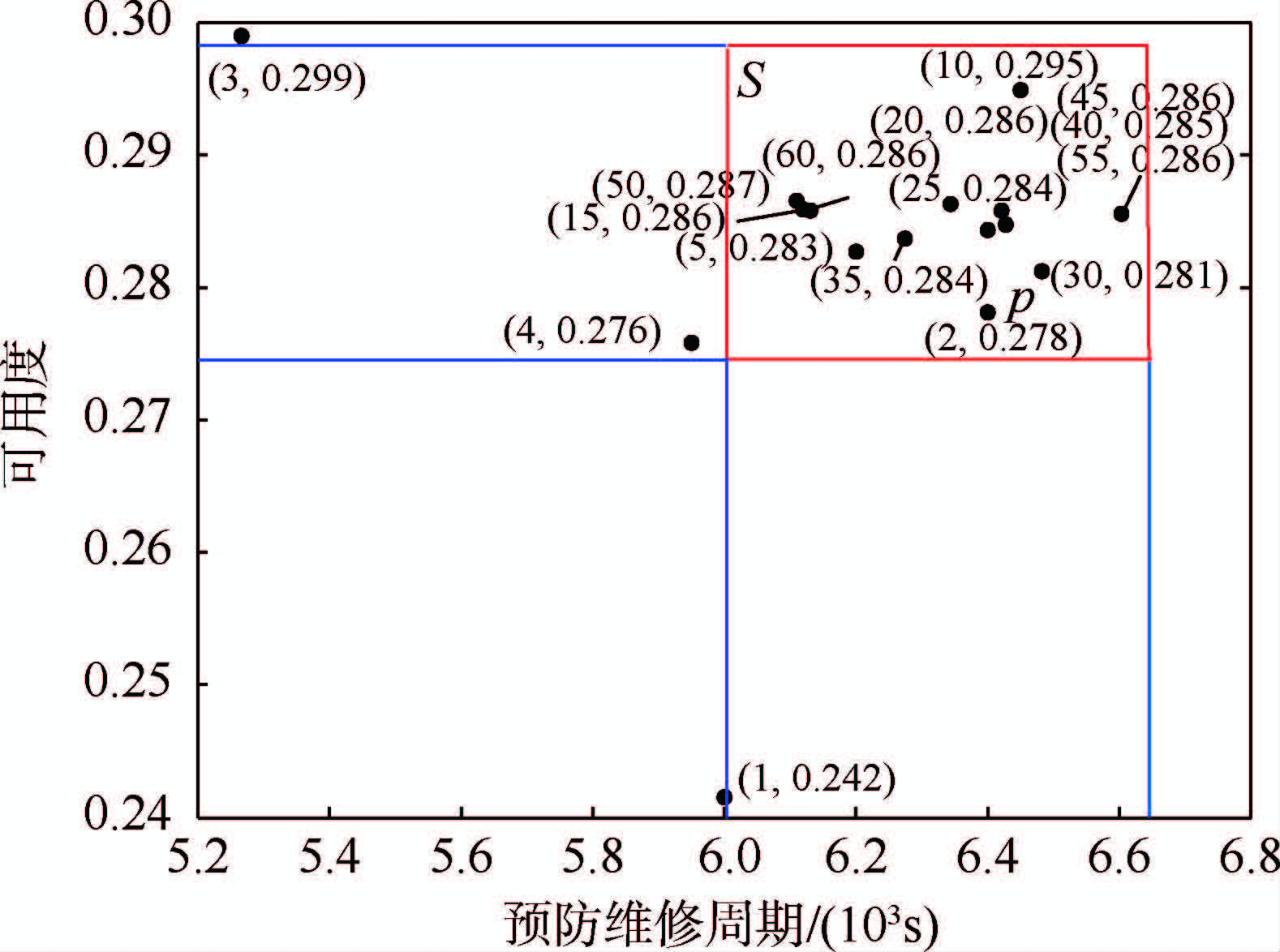
| 图 5 可用度、预防维修周期计算与仿真次数关系 Fig. 5 Relationship of availability, preventive maintenance time and simulation numbers |
由图 5可以看出,当仿真次数(图中括号内逗号前的数字)大于4时计算结果大致落在区域S内(图 5中仿真次数较少的p点也落在S区域,可能是由抽样随机性引起的).且由图 4和图 5的比较也可以发现,随着计算次数的增加,结果区间更加收紧,即平均最佳预防维修周期减弱了最大和最小预防维修周期数据对最终结果的影响.S区域内系统可用度变化范围(0.275~0.298),预防维修周期变化范围(6000~6620).可用度变化幅度为0.023,占到最低可用度8%左右.预防维修周期变化幅度为620,占到最低预防维修周期的10%,也就是仿真结果最差可能会使HPFTP丢失一次使用次数,鉴于安全性考虑,这样的结果可以接受.而且图中的S区域比较保守(因为S区域可以给得更小),所以计算次数大于5的结果已具有参考价值.文中计算进行了20次,求得平均最佳可用度为0.285,平均最佳预防维修周期是 6340s,即HPFTP预防维修前可重复使用12次.HPFTP一直在不断地升级更新,其相应年份的重复使用验证次数如表 5所示.
本文计算的HPFTP预防维修前可重复使用12次(包括可能出现故障并修复可用),HPFTP寿命期内的重复使用次数为

1) 可重复使用液体火箭发动机可用度的数字仿真方法可行,只要有其试验或/和使用数据,便可以仿真获得发动机或部件可用度指标的理论统计值,为确定系统或部件的最佳预防维修周期起到重要的理论支持.
2) 基本维修条件下,航天飞机主发动机高压液氢涡轮泵存在最佳的预防维修周期,平均最佳预防维修周期是6340s,理论上预防维修前可以重复使用12次.
3) 由于液体火箭发动机或其部件具有特殊的工作环境和严格的工作要求,其可用度比较低.计算表明,航天飞机主发动机高压液氢涡轮泵的平均最佳可用度仅为0.285.
4) 本文结果表明,在重复使用液体火箭发动机的研究中,如果一开始就从经济性和安全性等方面深入分析并确定平均最佳预防维修周期,则有助于避免系统研发初期可能出现因频繁维修或更换而导致的系统极低可用度和高成本的问题.
| [1] | Hartong A R,Rooney B D.Near-term RLV options,AIAA-2004-5947[R].Reston:AIAA,2004. |
| Click to display the text | |
| [2] | Williams W C.Report of the SSME assessment team,N93-21645[R].Washington,D.C.:NASA,1993. |
| [3] | Pauschke J M.Management of SSME hardware life utilization,NASA-N87-16777[R].Washington,D.C.:NASA,1986. |
| [4] | 金星,洪延姬,沈怀荣,等.工程系统可靠性数值分析方法[M].北京:国防工业出版社,2002:1-3. Jin X,Hong Y J,Shen H R,et al.Numerical analysis methods of reliability for engineering systems[M].Beijing:National Defense Industry Press,2002:1-3(in Chinese). |
| Cited By in Cnki | |
| [5] | 肖刚,李天柁.系统可靠性分析中的蒙特卡罗方法[M].北京:科学出版社,2003:5-9. Xiao G,Li T T.Monte Carlo method in the system reliability analysis[M].Beijing:Science Press,2003:5-9(in Chinese). |
| [6] | 杨为民,盛一兴.系统可靠性数字仿真[M].北京:北京航空航天大学出版社,1990:345-366. Yang W M,Sheng Y X.System reliability digital simulation[M].Beijing:Beihang University Press,1990:345-366(in Chinese). |
| [7] | 杨宇航,冯允成.复杂可修系统可靠性维修性综合仿真研究[J].系统仿真学报,2002,14(8):979-986. Yang Y H,Feng Y C.Complex repairable system reliability and maintainability simulation[J].Journal of System Simulation,2002,14(8):979-986(in Chinese). |
| Cited By in Cnki (38) | Click to display the text | |
| [8] | Blair J,Ryan R.Lessons learned in engineering,NASA/CR-216468[R].Huntsville,Alabama:Al Signal Research,Inc.,2011. |
| [9] | Hopson G.Atlantis STS-104 space shuttle program SSME flight readiness review,STS-104[R].Washington,D.C.:Space Shuttle SR & QA Assessment,2001. |
| [10] | Guure C,Ibrahim N.Methods for estimating the 2-parameter weibull distribution with type-I censored data[J].Research Journal of Applied Sciences,Engineering and Technology,2013,5(3):689-694. |
| Click to display the text | |
| [11] | Pasha G,Khan M,Pasha A.Empirical analysis of the Weibull distribution for failure data[J].Journal of Statistics,2006,1(13):33-45. |
| Click to display the text | |
| [12] | Paster R D,Stohler S L.SSME evolution,AIAA-1989-2618[R].Reston:AIAA,1989. |
| [13] | Jue F H.Space shuttle main engine-thirty years of innovation,NASA-46693[R].Canoga Park,CA.:Boeing Co.,2002. |
| Click to display the text | |
| [14] | Goldin D.Space shuttle main engine-NASA has not evaluated the alternate fuel turbopump costs and benefits,GAO/NSIAD-94-54[R].Washington,D.C.:Central Accounting Office,1993. |
| [15] | Charlers A M.Reusable rocket engine maintenance study,NASA-CR-165569[R].Hampton,Virginia:NASA-Lewis Research Center,1982. |
| Click to display the text | |
| [16] | Hale J R,Klatt F P.SSME improvements for routine shuttle operations,AIAA-85-1266[R].Monterey,California:American Institute of Aeronautics and Astronautics,1985. |
| [17] | Olorunniwo F.Scheduling imperfect preventive and overhaul maintenance[J].International Journal of Quality and Reliability Management,1991,8(4):67-79. |



