2. 清华大学航天航空学院, 北京 100084
2. School of Aerospace Engineering, Tsinghua University, Beijing 100084, China
直升机是一个多输入多输出强耦合的非线性系统.直升机控制器的效果依赖于飞行动力学模型的精度,并易受到外部扰动的影响.为了使直升机拥有较好的飞行品质,控制系统须拥有良好的解耦性和抗干扰.
直升机的耦合形式有操纵耦合和状态耦合两种,操纵耦合通常通过前馈矩阵进行解耦,状态耦合则通过输出反馈实现解耦.基于“一拍”实现跟踪的假设,文献[1, 2, 3, 4]计算了控制矩阵的逆,针对操纵耦合设计了矩阵形式的显模型跟踪飞行控制系统的内回路.基于传递函数形式的显模型跟踪思想,文献[5, 6]在UH-60A的总距、滚转、俯仰和偏航4个通道分别设计了独立的控制器,面向工程考虑了操纵耦合和状态耦合,但是并没有给出各通道之间的耦合系数的计算方法.文献[7]采用极点配置法设计了增稳和解耦控制器.基于悬停状态的降阶模型,文献[8]结合线性二次规划(LQR)和隐模型跟踪,采用极点配置法为阿帕奇直升机设计了解耦补偿器.基于H∞回路成形和混合灵敏度问题,文献[9]设计了双回路的控制系统,其姿态控制/姿态保持(ACAH)的内回路控制器用于各通道的解耦.文献[10]采用多目标遗传算法设计的直升机H∞鲁棒控制器具有较好的解耦性能.基于状态观测器的反馈和前馈控制律,文献[11]通过求解H∞代数黎卡提方程,设计了内回路的姿态控制器,实现了解耦控制并具有较高的飞行品质.
直升机系统总是存在着内部不确定性(建模误差)和外部不确定性(大气扰动)[12],因此直升机的控制系统也须拥有一定的综合抗扰能力.通过将系统内部不确定性和外部不确定性视为“总扰动”,并构造“扩张状态观测器(ESO)”对“总扰动”进行补偿,文献[13]提出了自抗扰控制(ADRC).随后基于线性扩张状态观测器(LESO),文献[14]提出了线性自抗扰控制(LADRC).由于LADRC整定参数较少，有利于实际应用,且大量研究表明LADRC对具有不确定性的复杂非线性系统仍有较好的控制效果[12].
鉴于此,本文提出了一种基于LADRC的姿态解耦控制方法.通过增加内回路反馈,采用3个单输入单输出的二阶LADRC控制器对滚转、俯仰和偏航3个姿态通道进行抗扰和操纵解耦控制,并基于频域和时域指标对参数进行了整定.
1 飞行动力学模型
1.1 各部件动力学模型 1.1.1 旋翼动力学模型
采用二阶形式的挥舞动力学方程[15]:
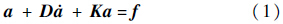
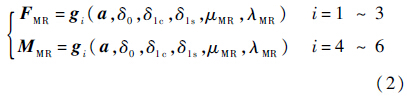
1.1.2 尾桨动力学模型
尾桨无周期变距,通过叶素理论得到尾桨六力素:
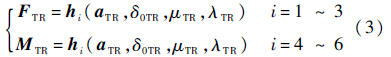
1.1.3 平尾、垂尾和机身动力学模型
平尾和垂尾产生的升力和阻力为
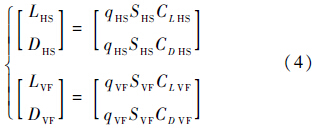
采用吹风试验[17]得到的气动力系数计算机身六力素,得到机身气动力FF和气动力矩MF.
1.2 全机飞行动力学模型
力、力矩方程以及运动学方程如下:
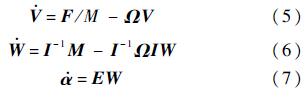
1.3 风 模 型
风模型采用美国军用标准MIL-F-8785C中的数学模型[19],包含了风切变模型、dryden紊流模型和突风模型.
2 配平和线性化
本文算例直升机为UH-60A,式(1)、式(5)~式(7)构成了非线性状态方程组$\dot X = f(X,U)$,其中U=[δ0 δ1c δ1s δ0TR]T为操纵输入，X=[V W α a $\dot a$]T为状态量.直升机悬停和稳定前飞时操纵量保持不变,而状态量的导数$\dot X$=0,通过求解非线性方程组即可实现配平.
图 1为本文计算配平值与AEFA飞行测试数据[20]的对比结果,其中μ为前进比.从图 1中可以看出本文计算值与飞行测试数据变化趋势基本吻合,由此说明本文飞行动力学模型和配平算法的正确性.本文仿真的初始状态和操纵量参见表 1所示的配平值.
 |
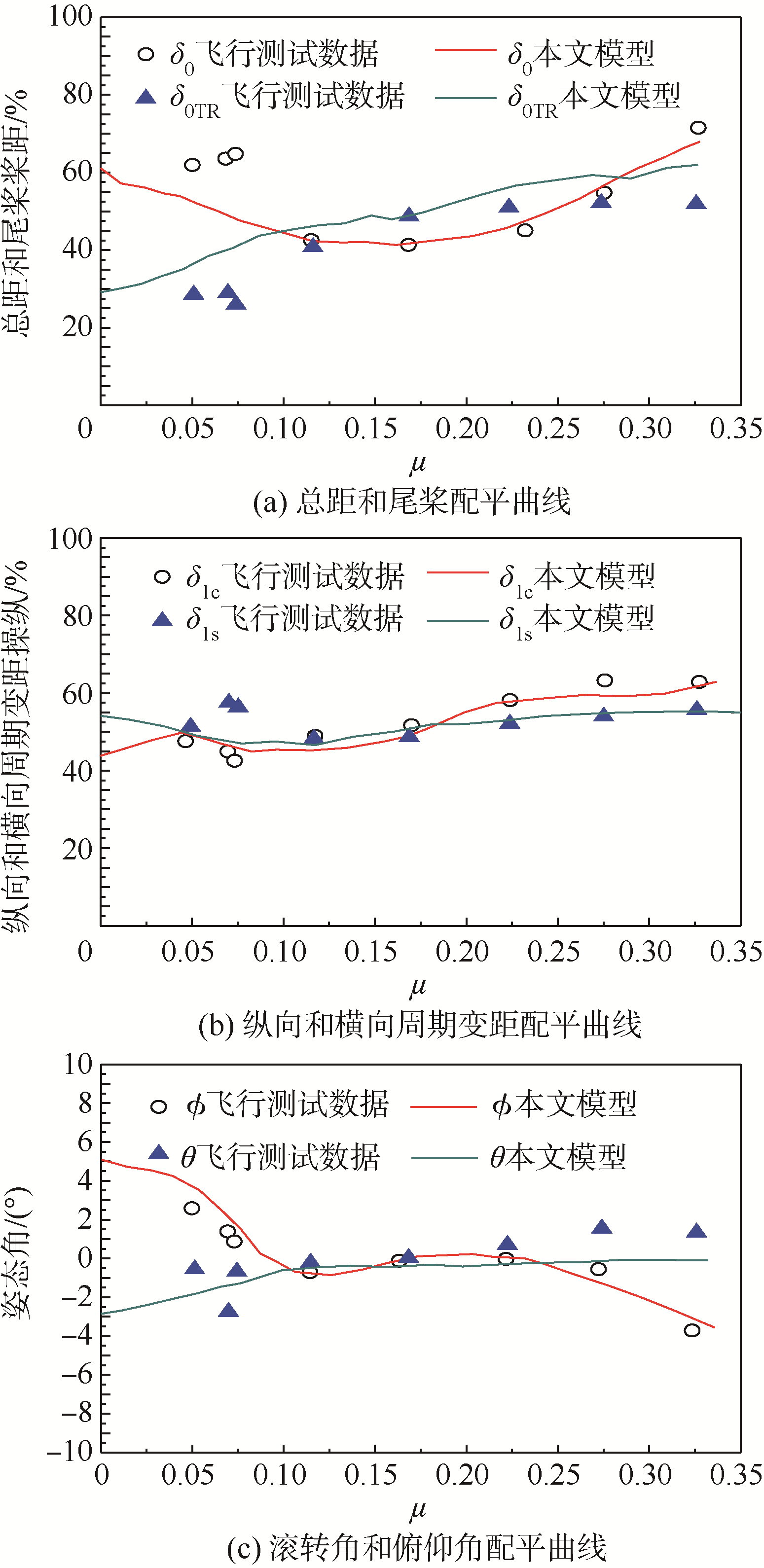| 图 1 配平结果曲线 Fig. 1 Curves of trim results |
| 飞行参数 | 数值 |
| V/(m·s-1) | [10 -0.017 0.451]T |
| W/(rad·s-1) | [0 0 0]T |
| α/rad | [-0.038 0.045 0]T |
| a/rad | [0.056 0.006 -0.016]T |
| U/% | [5.50 -0.232 -0.183 -1.48]T |
工程上通常基于小扰动理论和直升机在配平点附近为线性时不变系统假设来设计飞行控制系统.在表 1所示的配平状态对非线性方程组进行线性化处理,通过数值求偏导得到状态矩阵和控制矩阵:
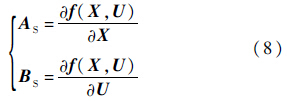
3 姿态解耦控制器的设计
3.1 LADRC解耦抗扰控制原理
LADRC继承了比例积分微分(PID)利用误差反馈进行控制的思想,利用LESO估计状态量和系统的总扰动(内、外扰动以及状态和控制耦合),将误差以及误差的高阶导数的线性组合作为控制率.
被控对象直升机为典型的多输出/多输出的耦合系统,可表示为如下形式[21]:
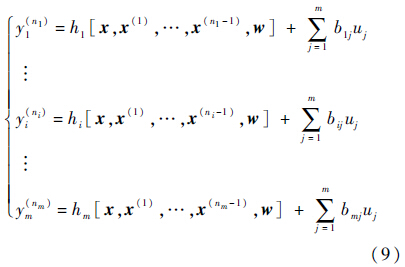
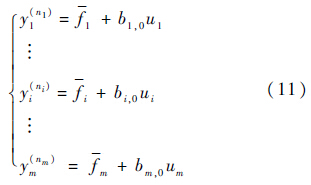
假设${\bar f_i}$可微,定义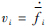
,定义一个新的状态向量$\tilde x$,定义其第j个分量$\tilde x$(j)=yi(j-1)(j=1,2，…，ni)和扩张状态量$\tilde x$(ni+1)=${\bar f_i}$,则第i个通道的状态方程形式如下:
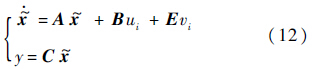
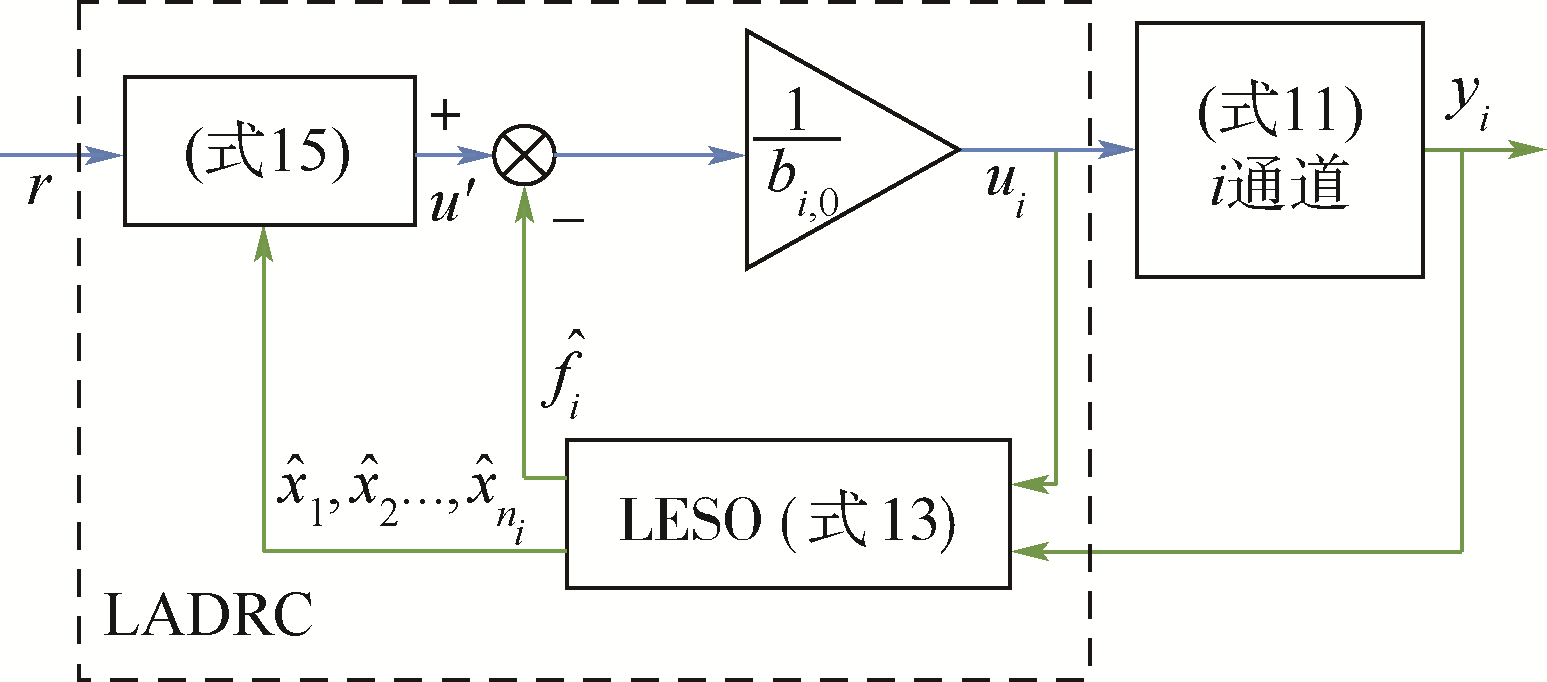
采用LESO对式(12)进行观测
 |
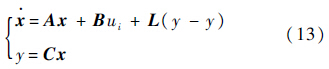
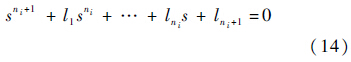
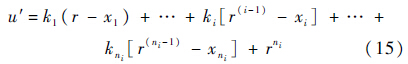
| 图 2 LADRC控制器框图 Fig. 2 Block diagram of LADRC controller |
3.2 基于LADRC的直升机姿态解耦控制
令X1=α,X2=W,Xr为其余状态向量,Xa=[δ1s δ1c δ0TR]T,则式(6)和式(7)可表示为
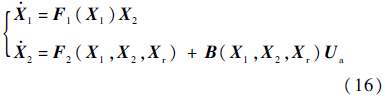
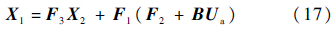
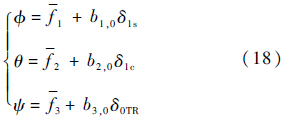
然而LADRC控制器只能保证BIBO稳定,只能对姿态输出的性能进行优化,不能保证内部其他状态量的性能,因此很难达到高的飞行品质.因此引入速度和角速度反馈回路,一方面为了提高飞行品质,另一方面由于反馈引入可以一定程度减弱状态耦合效应,使得控制器参数整定变得更加容易.
本文状态控制器设计将基于线化的状态空间方程组,图 3为UH-60A姿态解耦控制示意图.图中$\phi $LADRC、θLADRC和ψLADRC均为二阶LADRC控制器,各通道的控制结构如图 2所示.Δ$\phi $r、Δθr和Δψr分别为3个通道增量形式的参考信号,3个独立控制器分别控制滚转、俯仰和偏航通道增量形式的姿态角Δ$\phi $、Δθ和Δψ.KS为3×6的反馈增益矩阵.速度和角速度增量构成的信号Δxa=[ΔV ΔW]T乘以KS得到反馈信号KSΔxa,反馈信号与3个LADRC控制器给出的控制信号[Δδ1c Δδ1s Δδ0TR]T叠加,构成了姿态控制信号ΔUa,总距控制信号Δδ0为0(总距操纵不直接控制姿态角).
 |
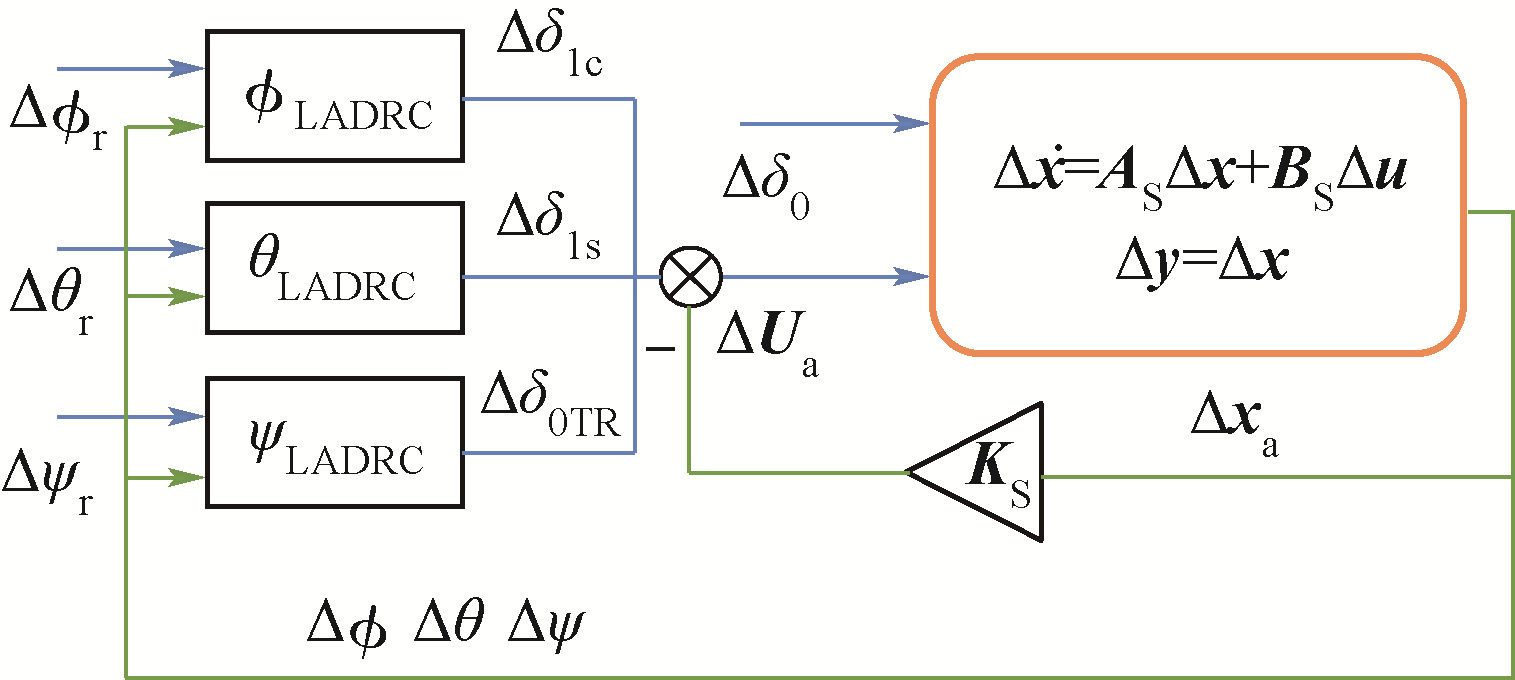| 图 3 带反馈内回路的姿态控制器 Fig. 3 Attitude controller with inner feedback loop |
3.3 参数整定
在参数整定中,输入和状态量均为相对配平点的增量.定义3个姿态通道的单位阶跃响应的误差平方和为目标函数:
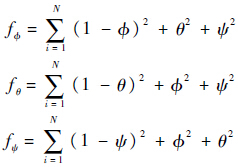
1) 稳定性约束st.1.
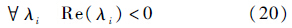
2) 3个通道带宽约束st.2.
 |
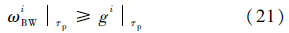
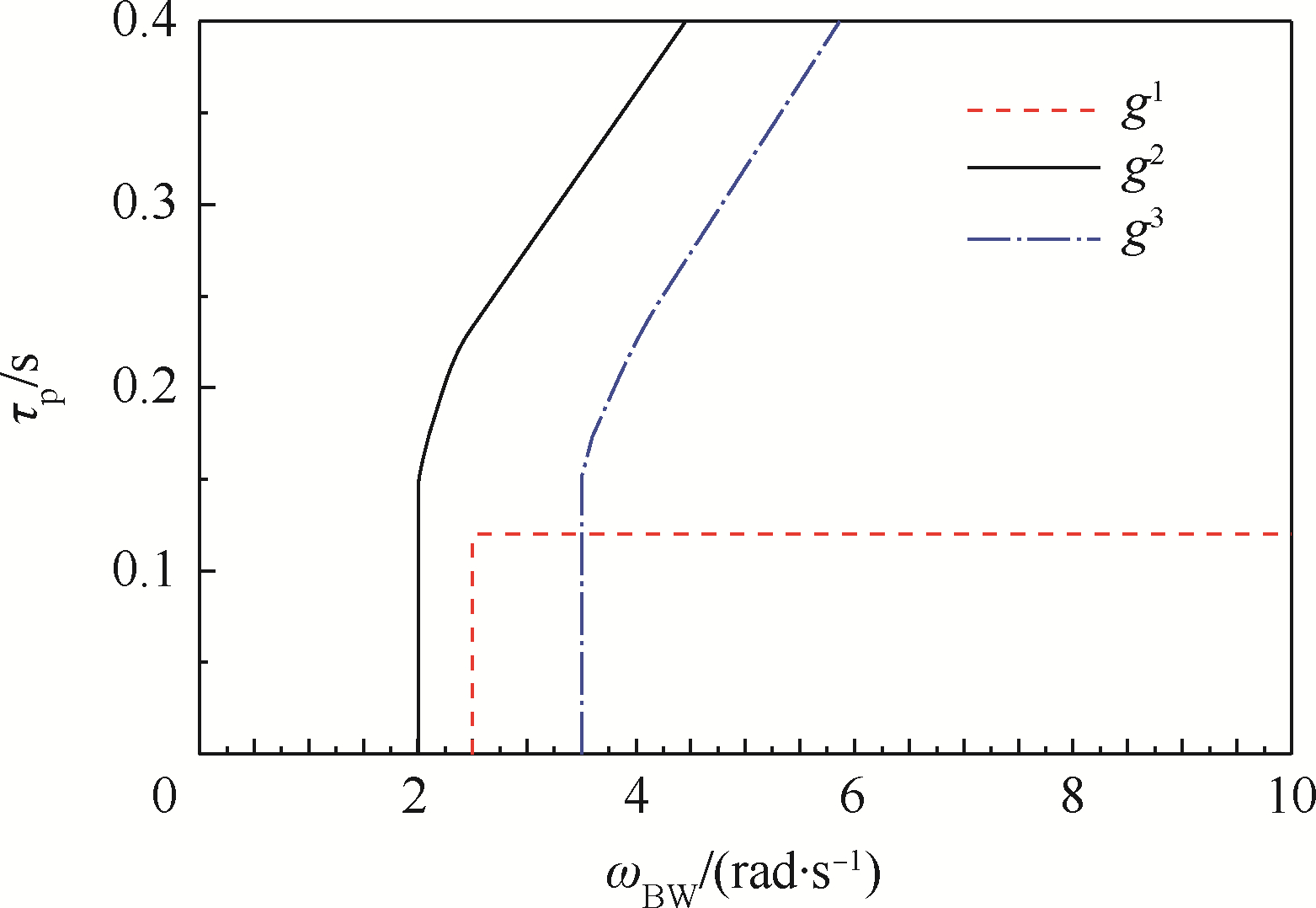| 图 4 带宽一级飞行品质边界线 Fig. 4 Border lines for bandwidth flight quality 1 |
3) 俯仰和滚转耦合约束st.3.
4) 快捷性约束st.4.
 |
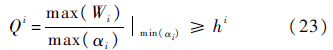
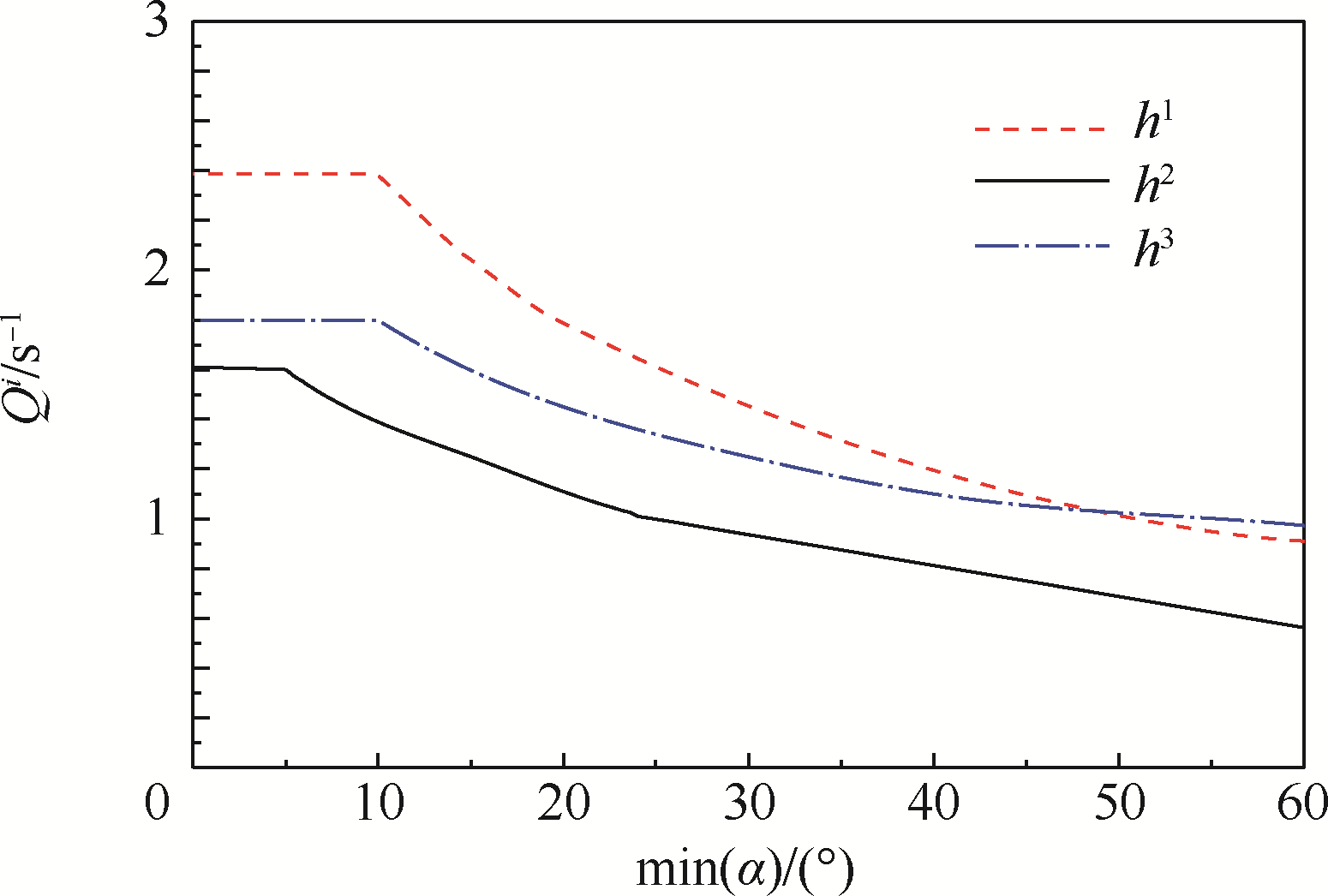| 图 5 快捷性一级飞行品质边界线 Fig. 5 Border lines for quickness flight quality 1 |
5) 抗干扰约束st.5.
由此LADRC的姿态解耦控制系统的参数整定问题转化为目标函数的约束优化问题.每个姿态通道的LADRC控制器有4个待定参数,3个通道共12个,反馈增益矩阵KS有18个未知元素,因此共有30个参数需要整定.引入罚函数[10],定义新的目标函数
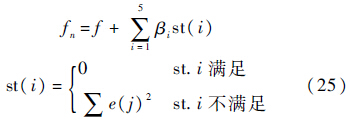
为了避免优化对初值的依赖和易陷入局部最优解,本文采用H∞综合算法[25]计算出控制器和反馈阵待整定参数的初值,该算法具有较好的全局收敛性和较快的收敛速度,但是该算法只能对稳定性、跟踪响应速度、超调量以及稳定裕度等进行约束,因此只能满足一级飞行品质的部分约束条件.随后基于式(25),采用最速下降算法进行优化,计算步骤如下:
1) 调入上述计算的参数初值,给定终止误差ε=1×10-5,k=0.
2) 计算梯度$\nabla {f_n}\left( {{x^k}} \right)$,若$\nabla {f_n}\left( {{x^k}} \right) \le \varepsilon $,迭代结束,输出xk,否则进入步骤3).
3) 对${f_n} = \left( {{x^k} + {t_k}{p^k}} \right) = \min {f_n}\left( {{x^k} + t{p^k}} \right)$进行一维寻优,求解tk,其中${p^k} = - \nabla {f_n}\left( {{x^k}} \right),t > 0$.
4) 计算${x^{k + 1}} = {x^k} + {t_k}{p^k}$,令k=k+1,返回步骤2).
3.4 计算结果与品质评估
通过对目标函数的优化计算实现了LADRC控制器和反馈回路的参数整定,LADRC控制器参数如表 2所示,反馈矩阵如下:
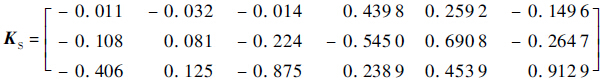
| 控制器 | k1 | ωo | k2 | bi,0 |
| $\phi $LADRC | 74.24 | 6.8 | 3.01 | 0.54 |
| θLADRC | 29.27 | 7.33 | 4.23 | 1.28 |
| ψLADRC | 40.83 | 6.47 | 3.57 | 0.52 |
1) 特征值位置.
对开环系统的状态矩阵A求解特征值,其中长周期发散模态对应特征值为:0.082±0.323i,实部为正不满足st.1.图 6为加上本文设计的控制器后闭环特征值的位置.由于旋翼挥舞动力学对应6个特征根实部为大的负数,故忽略其运动模态,图 6中共有18个闭环极点,每个姿态通道的LADRC控制器产生3个极点,3个通道的控制器共产生9个极点,其余9个极点对应直升机的机体运动模态(线速度、角速度和欧拉角),这18个特征值中特征值实部最大的为-0.022,满足st.1,系统稳定.
 |
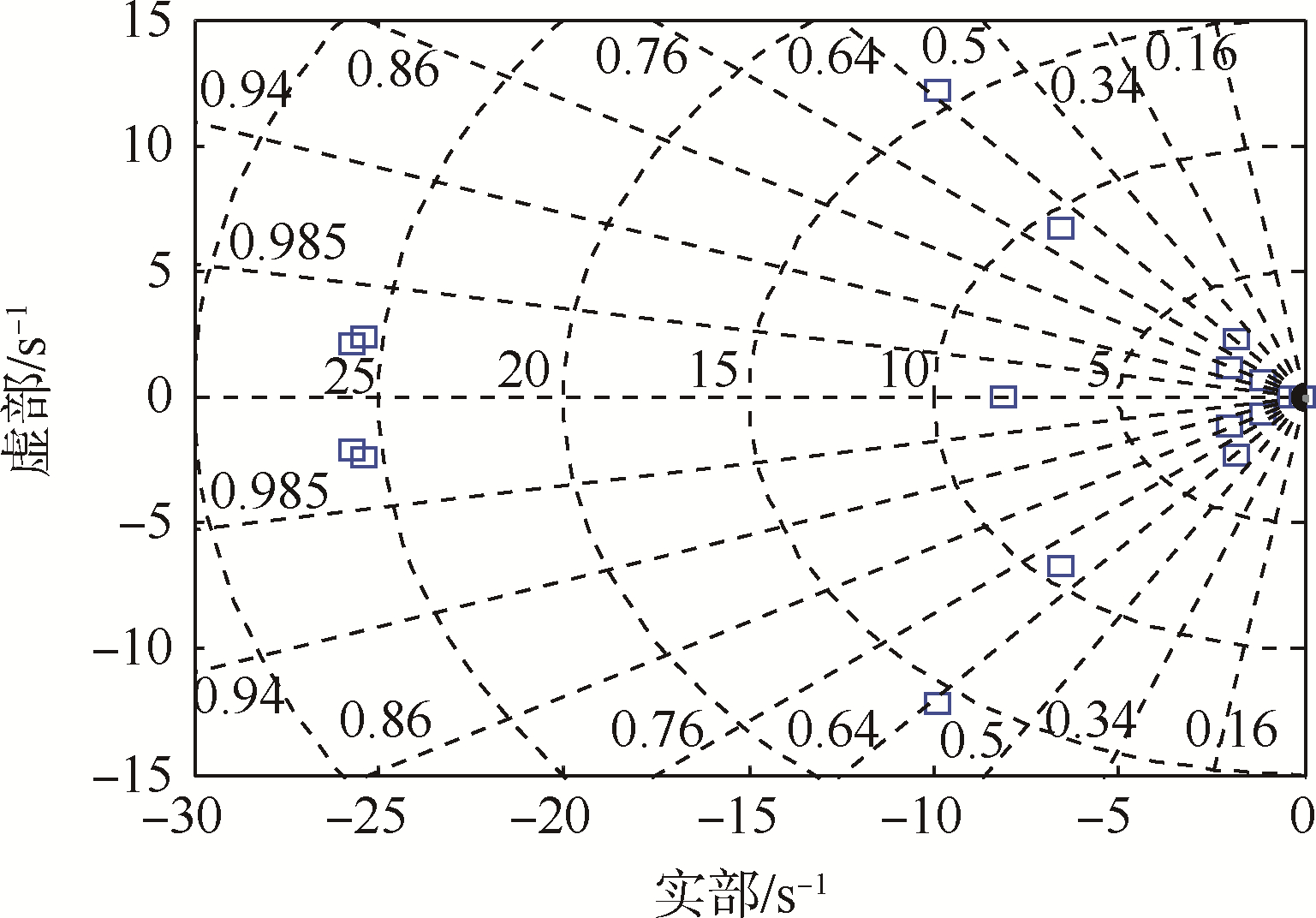| 图 6 闭环系统特征值 Fig. 6 Eigenvalues of closed-loop system |
2) 带宽和延迟.
图 7～图 9为滚转、俯仰和偏航3个通道的频响,由图易知3个通道带宽和相位滞后时间分别为:滚转通道ωBW=8.94 rad/s,τp=0.054 s;俯仰通道ωBW=5.87 rad/s,τp=0.022 s;偏航通道ωBW=4.61 rad/s,τp=0.067 s.按照ADS-33E-PRF的品质规范,3个姿态通道均达到了一级品质的标准(参见下文品质评估结果汇总,采用类似于CONDUIT[26]图形方式显示).
 |
| 图 7 滚转通道频响 Fig. 7 Frequency response of roll channel |
 |
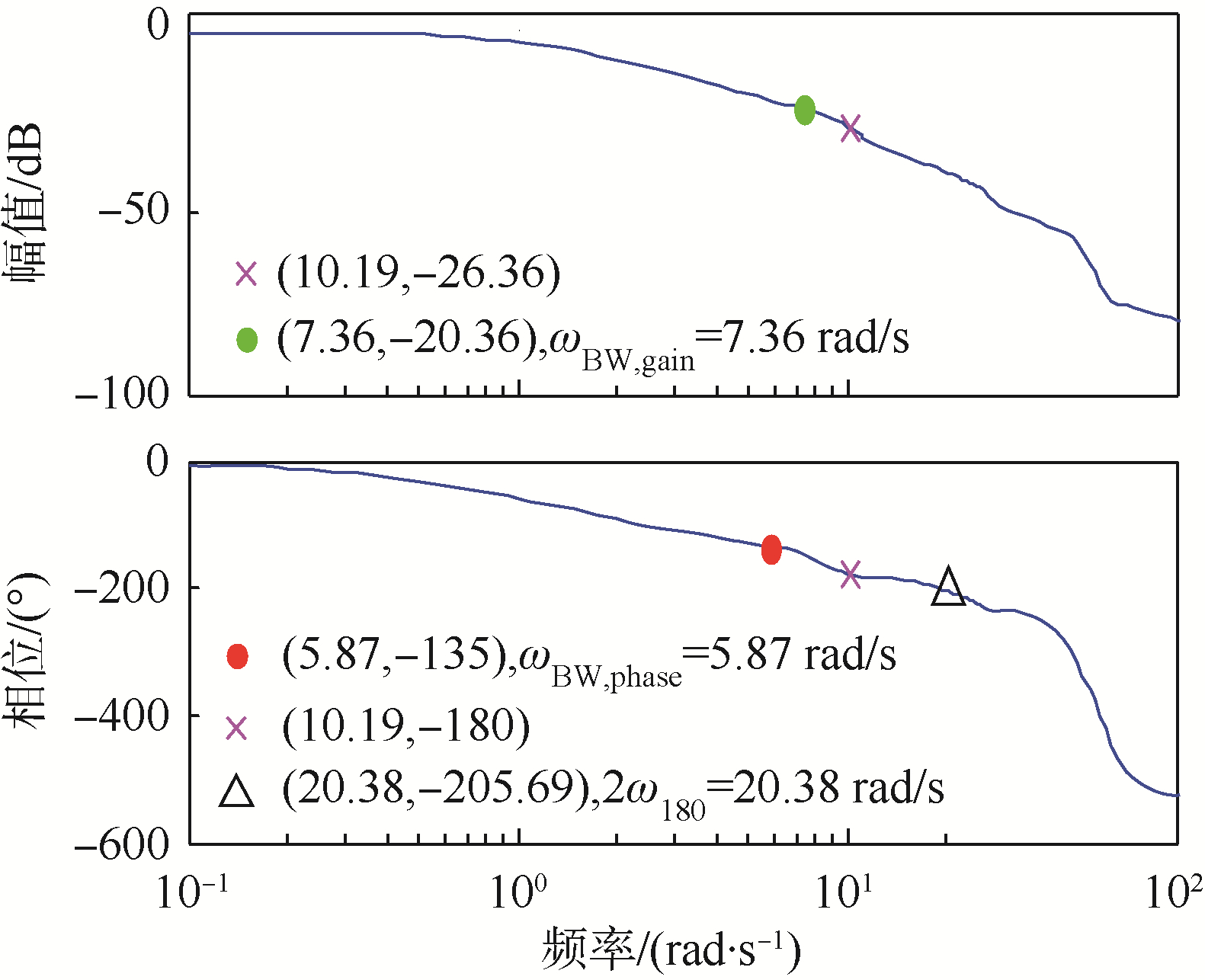| 图 8 俯仰通道频响 Fig. 8 Frequency response of pitch channel |
 |
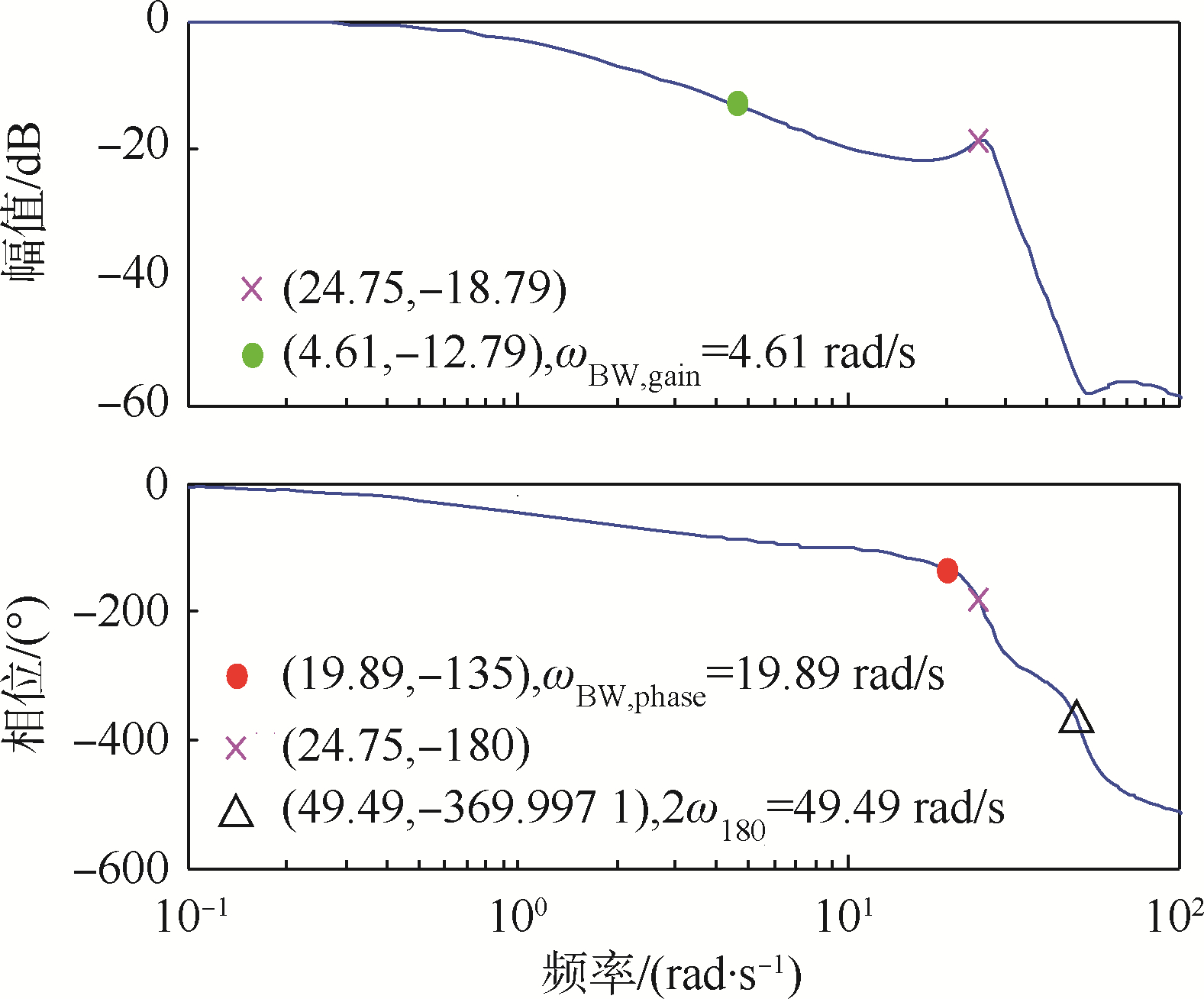| 图 9 偏航通道频响 Fig. 9 Frequency response of yaw channel |
3) 俯仰和滚转耦合.
在滚转、俯仰通道分别输入0.15 rad的阶跃信号,图 10和图 11为相应姿态响应.耦合系数:kpitch/roll=0.040 9,kroll/pitch=0.086 2,均达到了一级飞行品质(参见下文品质评估结果汇总).由图 10和图 11同样可以看出俯仰、滚转与偏航通道耦合作用也非常小.
 |
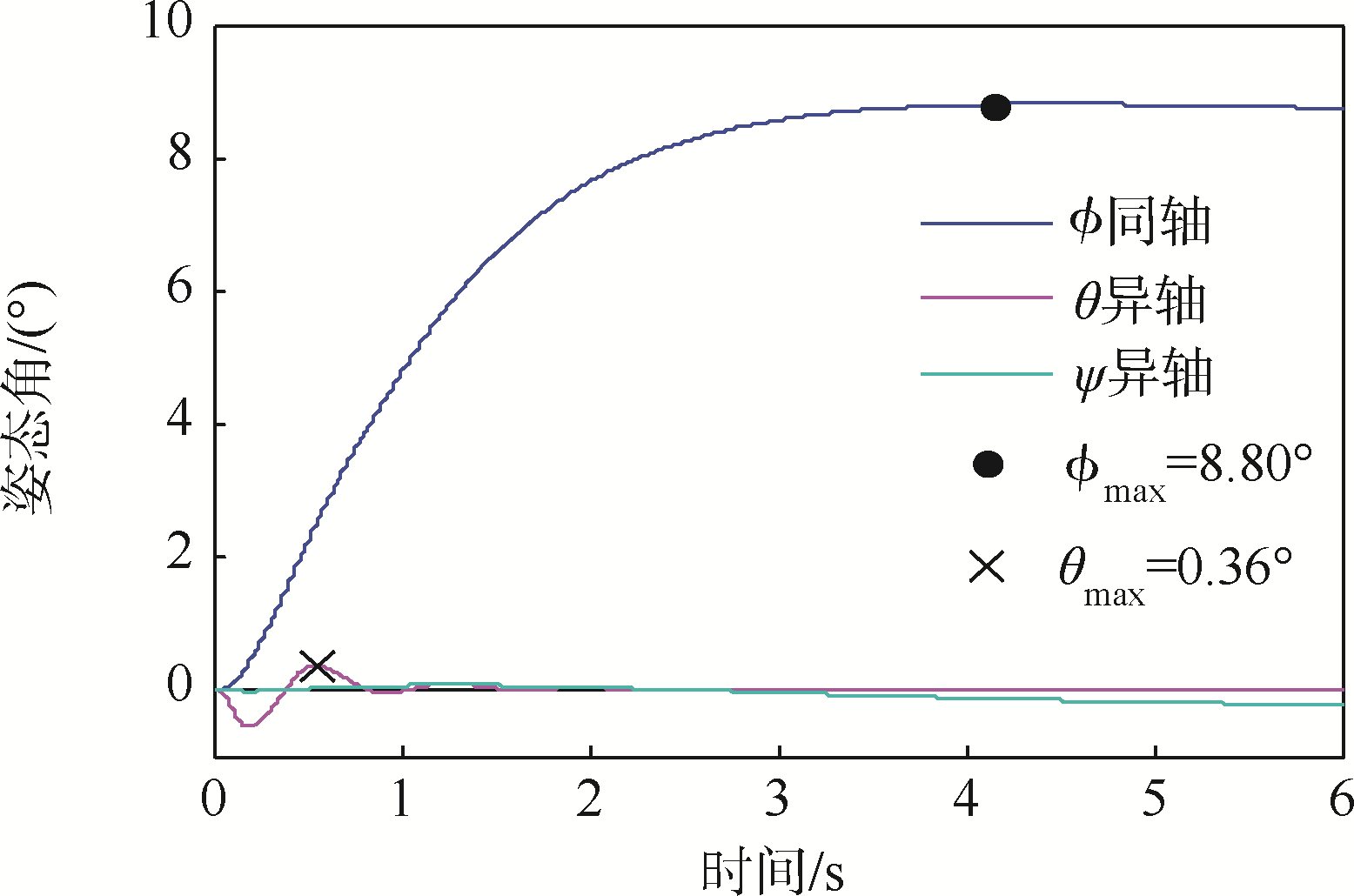| 图 10 滚转通道阶跃输入下的耦合 Fig. 10 Coupling effects with a step input of roll channel |
 |
| 图 11 俯仰通道阶跃输入下的耦合 Fig. 11 Coupling effects with a step input of pitch channel |
4) 快捷性.
对3个通道分别施加尖峰输入,图 12~图 14为三轴姿态通道响应,根据快捷性定义计算,3个姿态通道的快速比分别为Q1=2.52,Q2=2.06和Q3=2.42,达到了一级品质(参见下文品质评估结果汇总).
 |
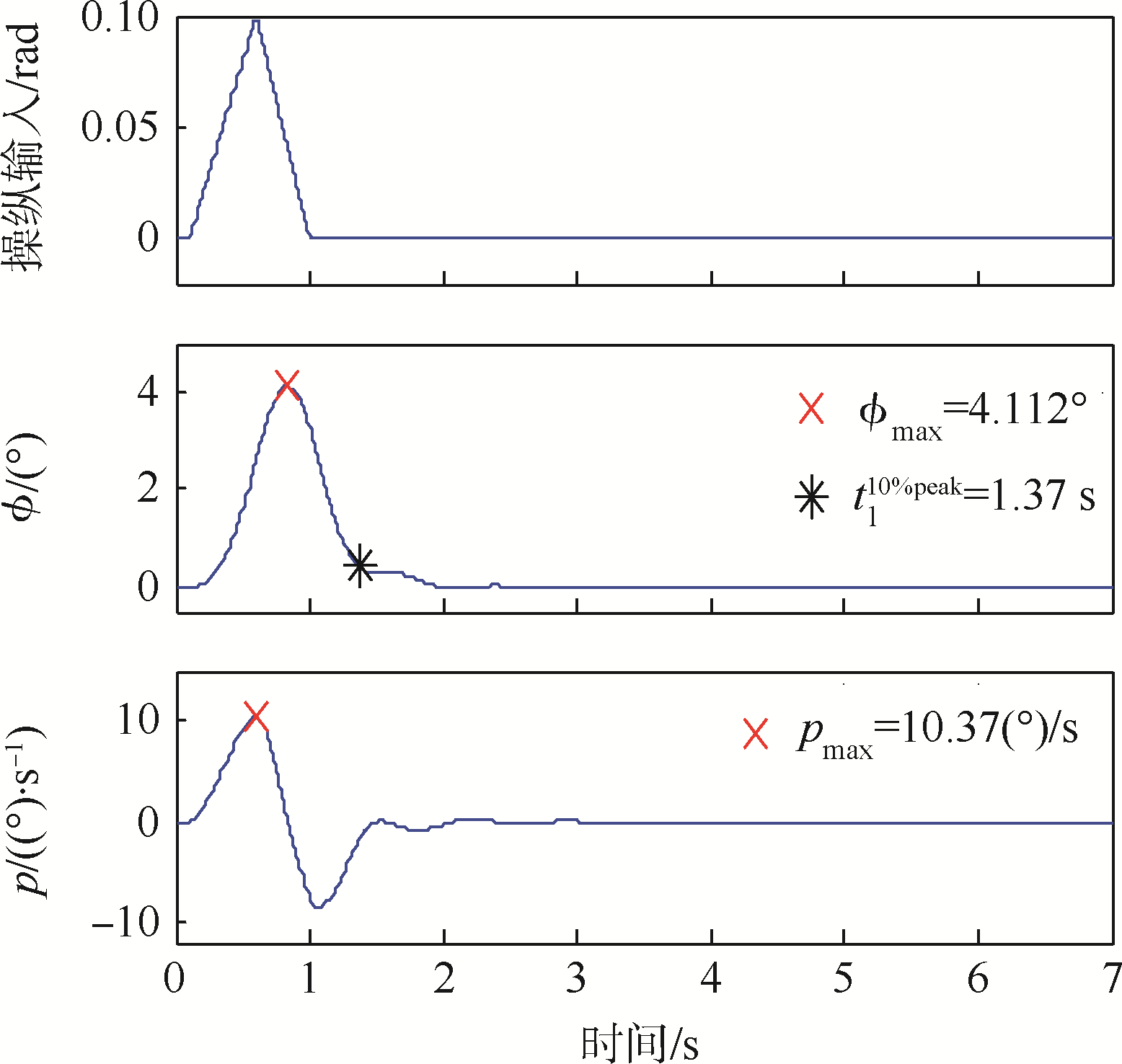| 图 12 滚转通道尖峰输入响应 Fig. 12 Spike input response of roll channel |
 |
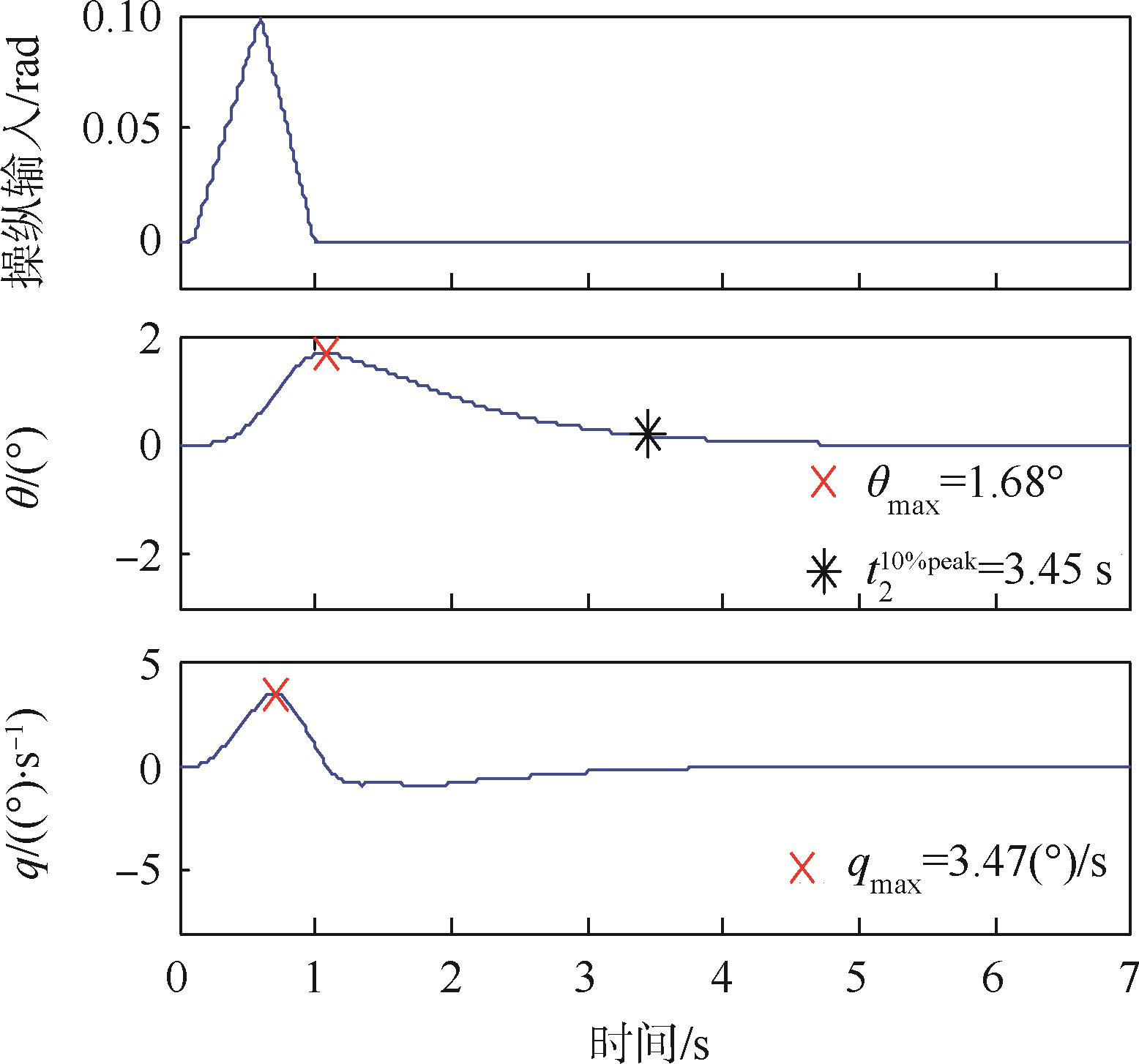| 图 13 俯仰通道尖峰输入响应 Fig. 13 Spike input response of pitch channel |
 |
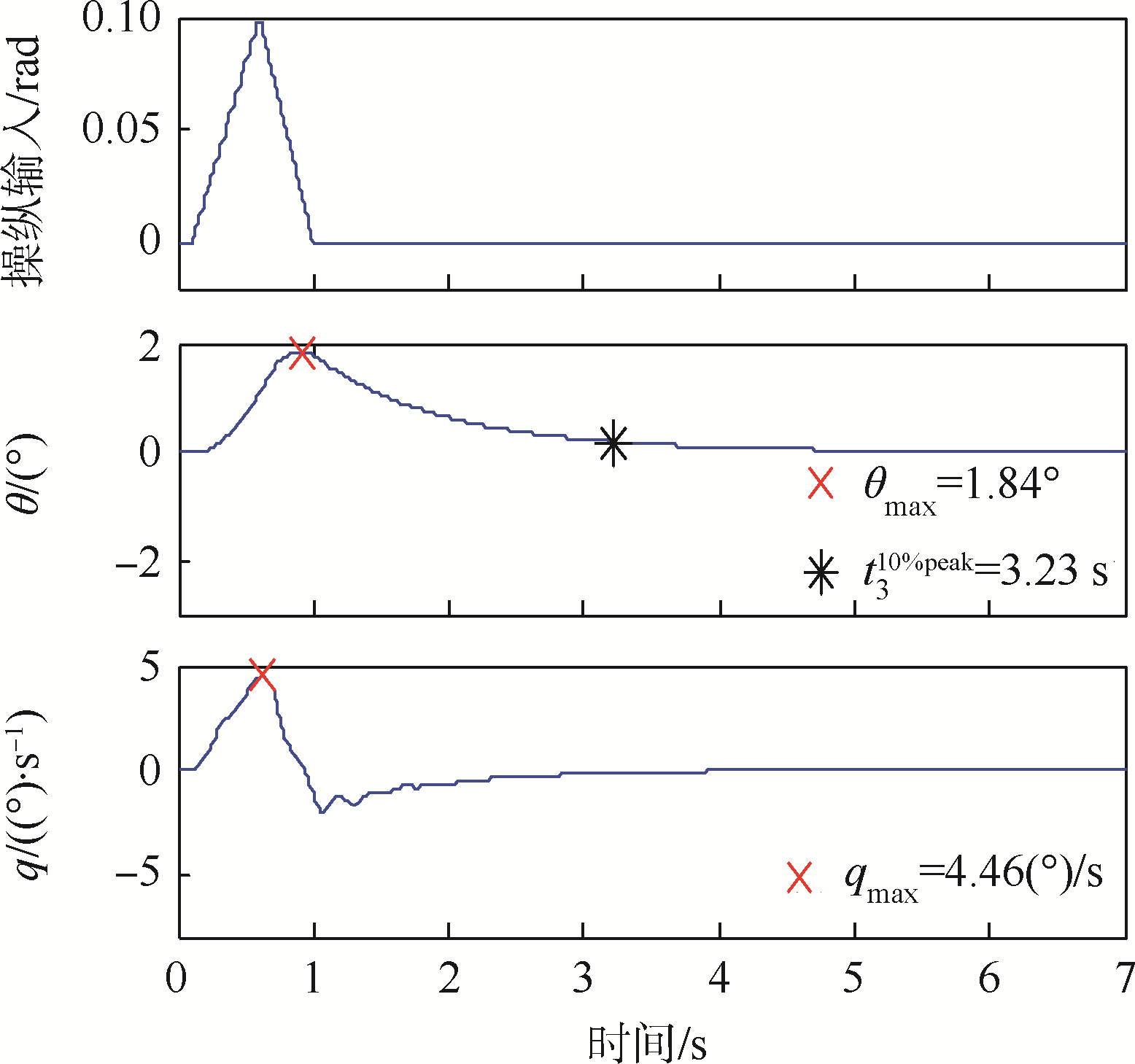| 图 14 偏航通道尖峰输入响应 Fig. 14 Spike input response of yaw channel |
5) 抗干扰性.
若将上述3个尖峰信号视为扰动,则由图 12～图 14可知干扰后的姿态回复到10%的时间分别为1.37、3.45和3.23 s,远小于一级品质规定的10 s(参见下文品质评估结果汇总).
上述控制器设计、参数整定以及品质评估均是基于线化方程.图 15则为基于非线性动力学方程的控制器,在前向通道需叠加上配平量Utrima,反馈回路需减去对应配平值xtrima.
 |
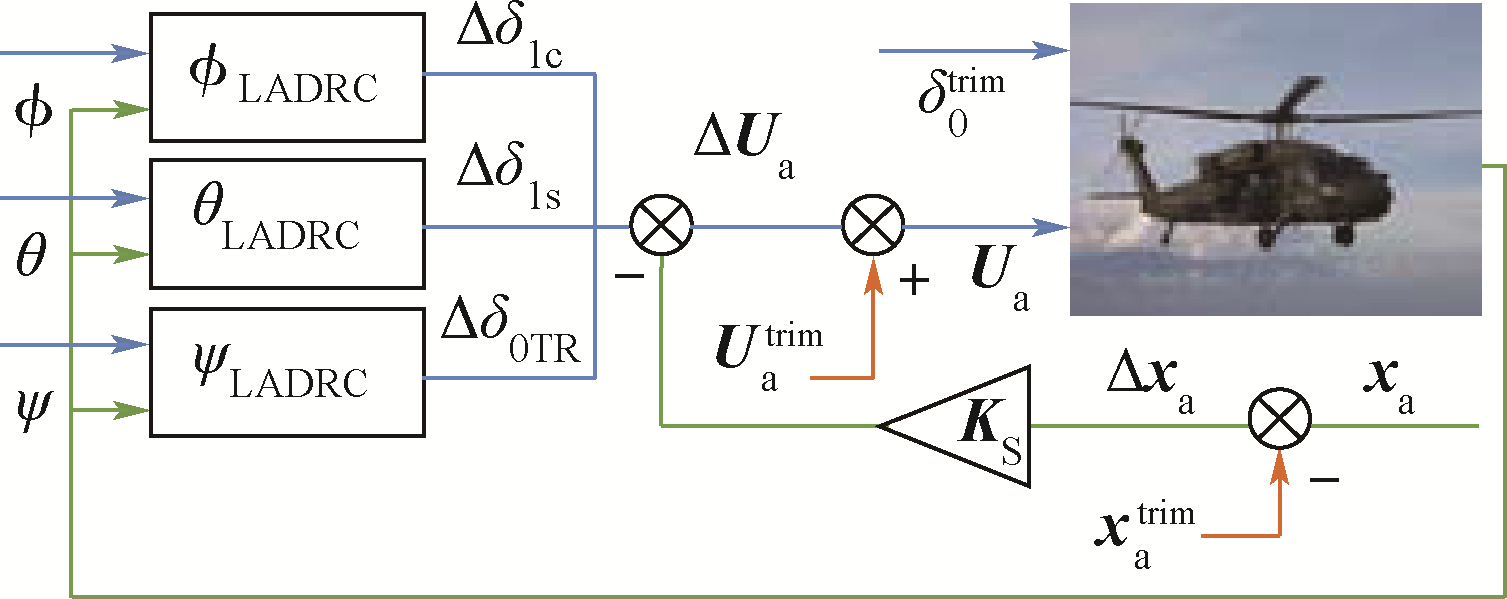| 图 15 非线性动力学的姿态控制器 Fig. 15 Attitude controller for nonlinear dynamics |
为了更好地模拟真实飞行环境,引入图 16所示的大气扰动.风切变模型中6 m高度风速和风向设置为1 m/s和0°(向北);dryden紊流模型中6 m高度风速和风向设置为5 m/s和0°;突风模型中设置突风开始时间为0 s,幅值为[3.53.03.0]m/s.
 |
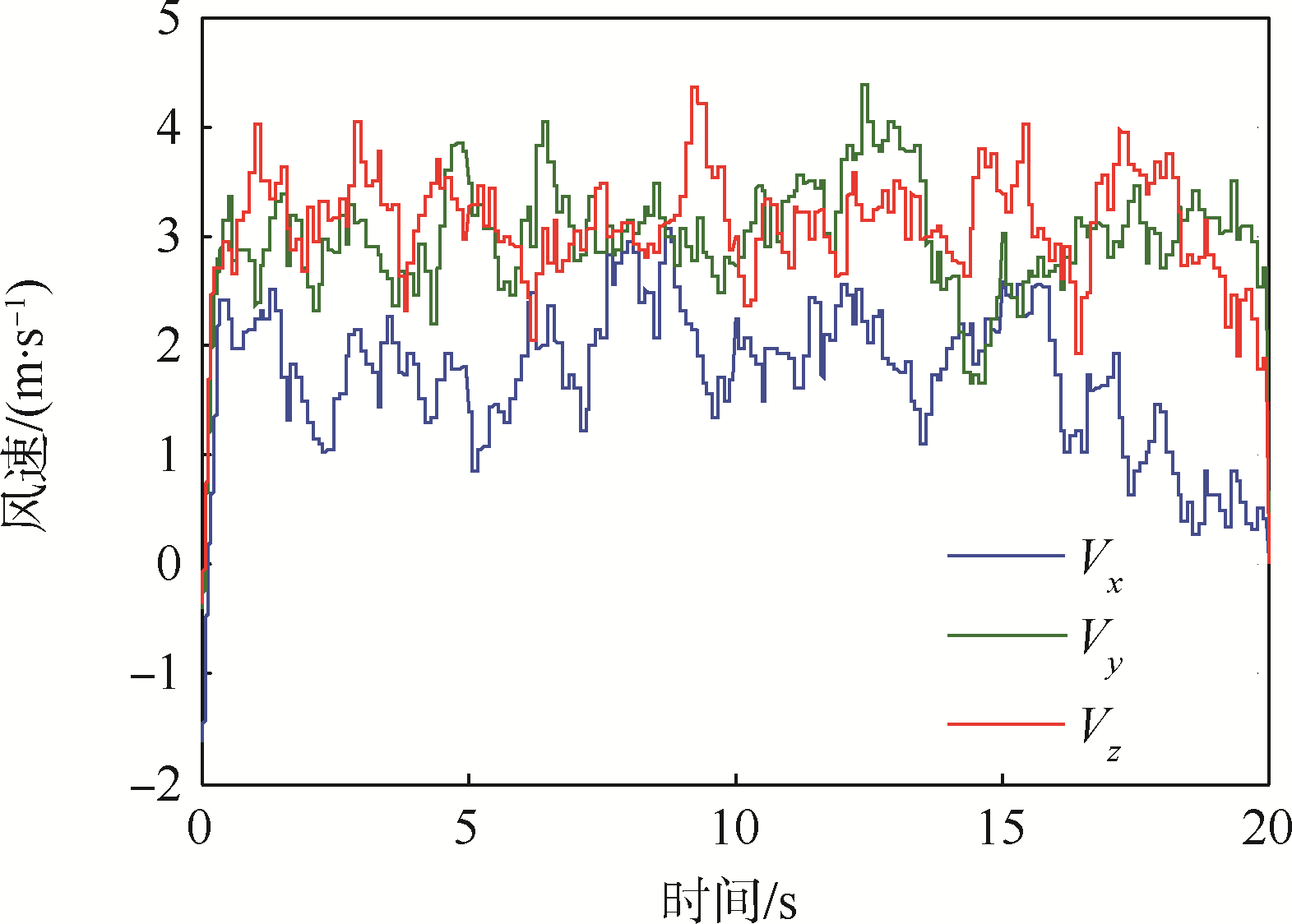| 图 16 地面坐标系下的风扰动 Fig. 16 Wind disturbance in ground coordinate system |
图 17为风扰下的UH-60A姿态响应,图中可以看到滚转、俯仰和偏航三轴姿态始终保持在平衡状态附近,最大扰动不超过0.004 rad,姿态解耦控制器对于非线性系统仍具有较好的抗扰性.
 |
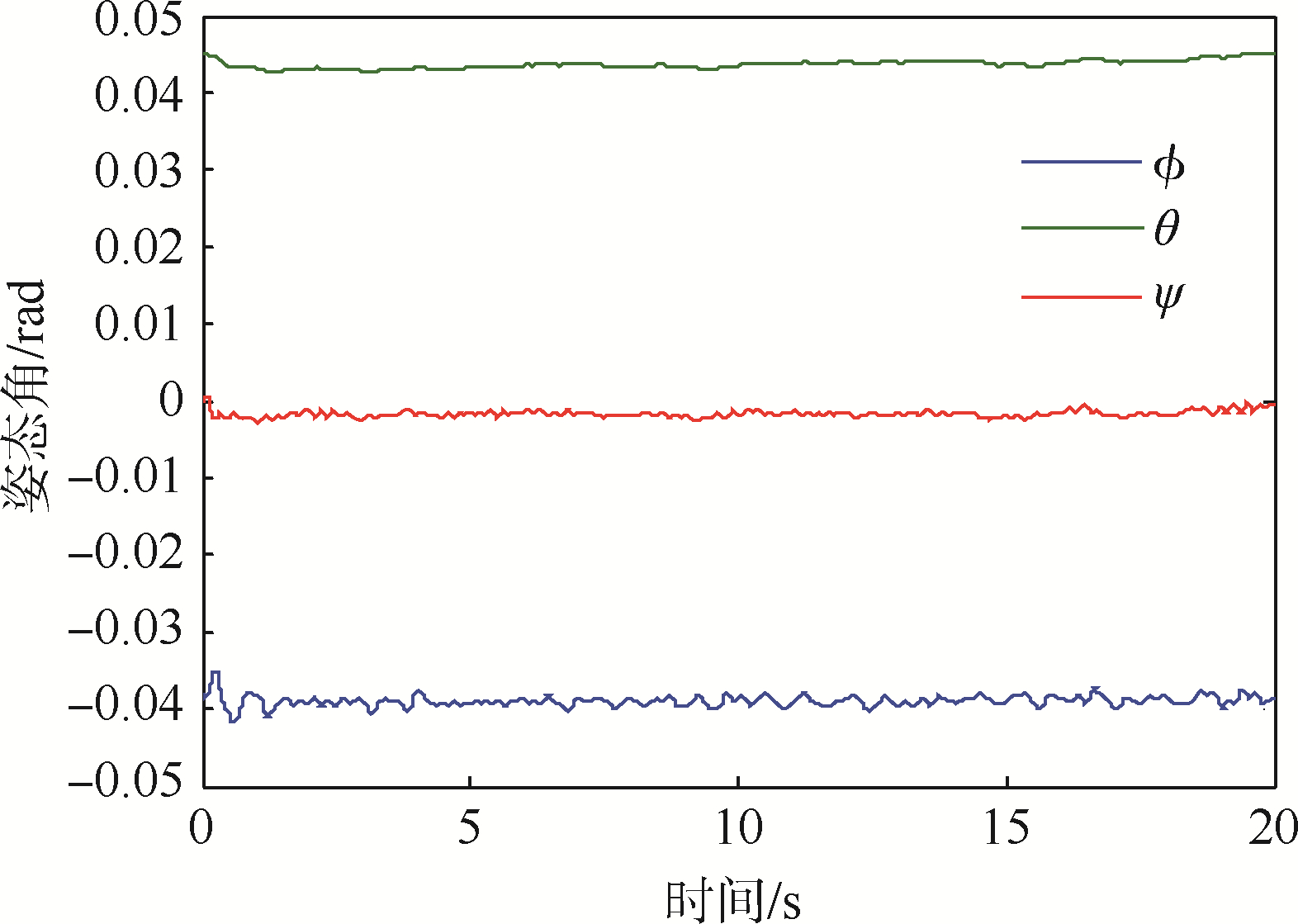| 图 17 风扰下的姿态保持 Fig. 17 Attitude hold with wind disturbance |
图 18为飞行品质规范评估结果汇总,从图中可见本文搭建的姿态控制器在带宽、耦合以及快捷性等方面都具有一级飞行品质,具有较优的性能.
 |
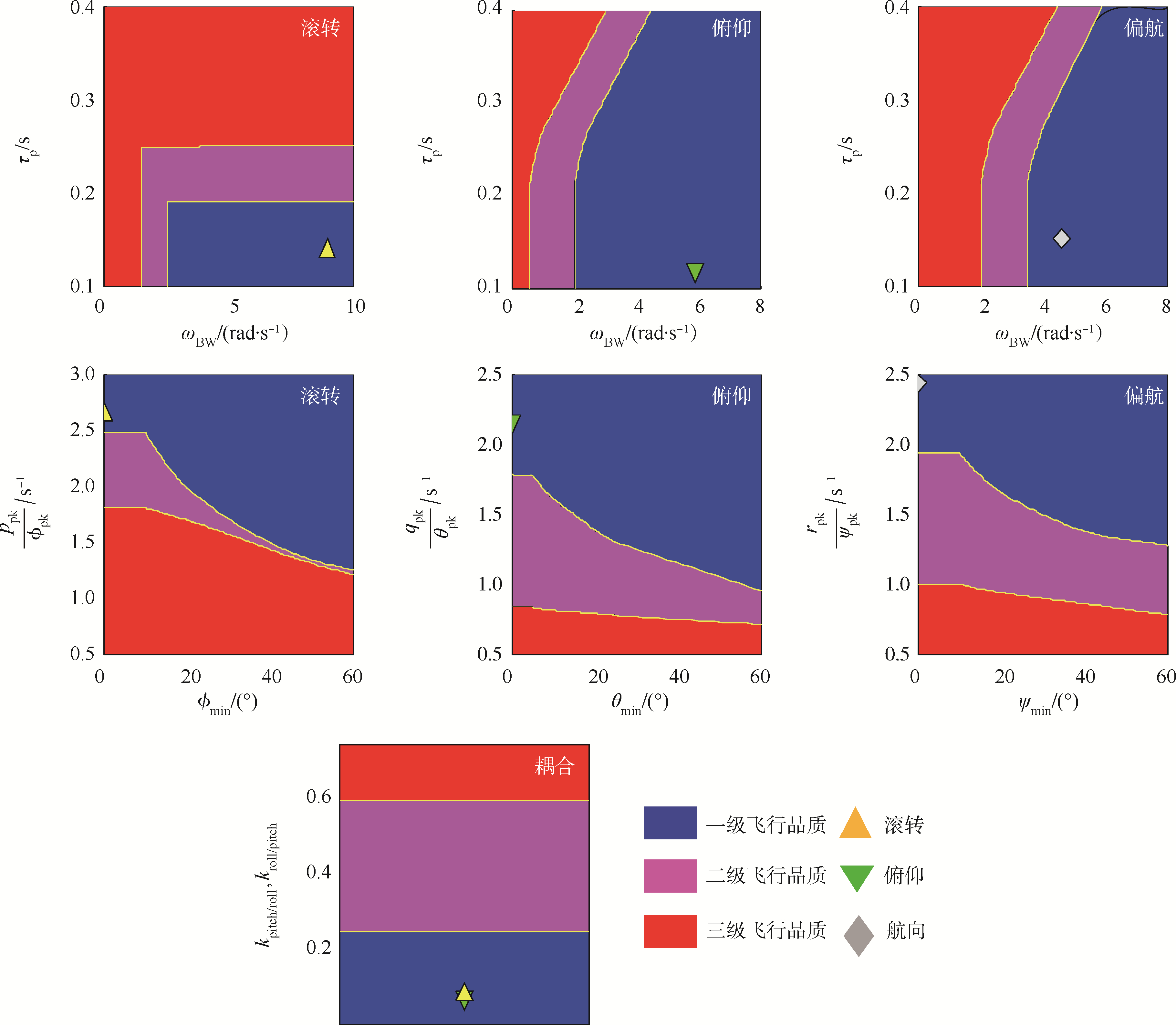| 图 18 姿态控制器飞行品质评估结果汇总 Fig. 18 Summary of flight quality evaluation results for attitude controller |
4 结 论
1) 引入速度和角速度反馈回路,基于单输入单输出的二阶LADRC控制器进行控制器的设计可以实现姿态通道的解耦控制.
2) 建立目标函数并基于ADS-33E-PRF引入约束,将LADRC控制器和反馈增益矩阵的参数整定变为约束优化问题，并对经参数优化后的控制器进行了评估,剪裁出的各项品质指标均达到了一级标准.
3) 基于LADRC的姿态控制器使得直升机在风扰下仍有较好的直升机的姿态保持能力,具有较好的抗扰性.
| [1] | Bouwer G, Hilbert K B.A piloted simulator investigation of decoupling helicopters by using a model following control system, AD-A139976[R].Virginia:ASTIA, 1984. |
| Click to display the text | |
| [2] | Hilbert K B, Bouwer G.The design of a model-following control system for helicopters[C]//17th Fluid Dynamics, Plasma Dynamics, and Lasers Conference.Reston:AIAA, 1984:601-617. |
| Click to display the text | |
| [3] |
袁锁中,杨一栋.一拍跟踪的直升机显模型跟踪解耦控制系统设计[J].直升机技术, 1997(1):27-32. Yuan S Z, Yang Y D.Design of a model following control system for helicopter[J].Helicopter Technique, 1997(1):27-32(in Chinese). |
| Cited By in Cnki (1) | |
| [4] |
郑峰婴,杨一栋.控制阵解耦的直升机显模型跟踪飞控系统设计[J].海军航空工程学院学报, 2007, 22(1):119-124. Zheng F Y, Yang Y D.Flight control system design of explicit model-following for helicopter based on control distribution matrix decouple[J].Journal of Naval Aeronautical Engineering Institute, 2007, 22(1):119-124(in Chinese). |
| Cited By in Cnki (5) | |
| [5] | Landis K, Glusman S.Development of ADOCS controllers and control laws:Vol 1-3, NASA-CR-17739[R].Washington, D.C.:NASA, 1987. |
| [6] | Tischler M B, Fletcher J W, Morris P M, et al.Applications of flight control system methods to an advanced combat rotorcraft, NASA-TM-101054[R].Washington, D.C.:NASA, 1989. |
| Click to display the text | |
| [7] | Manness M A, Murray-Smith D J.Aspects of multivariable flight control law design for helicopters using eigenstructure assignment[J].Journal of the American Helicopter Society, 1992, 37(3):18-32. |
| Click to display the text | |
| [8] | Hicks K L, Rodriguez A A.Decoupling compensation for the Apache helicopter[C]//Proceedings of the IEEE Conference on Decision and Control.Piscataway, NJ:IEEE Press, 1996, 2:1551-1555. |
| Click to display the text | |
| [9] | Ji S Y, Wu A G.Study on dual-loop controller of helicopter based on the robust H-infinite loop shaping and mixed sensitivity[C]//2011 International Conference on Electrical and Control Engineering.Piscataway, NJ:IEEE Press, 2011:1291-1294. |
| Click to display the text | |
| [10] |
邢小军,闫建国,张洪才.直升机H∞鲁棒控制器的优化设计及仿真[J].系统仿真学报, 2010, 22(9):2185-2189. Xing X J, Yan J G, Zhang H C.Design and simulation for helicopter's optimal H infinity robust controller[J].Journal of System Simulation, 2010, 22(9):2185-2189(in Chinese). |
| Cited By in Cnki | |
| [11] | Wang B, Chen B M, Lee T H.An RPT approach to time-critical path following of an unmanned helicopter[C]//8th Asian Control Conference-Final Program and Proceedings.Piscataway, NJ:IEEE Press, 2011:211-216. |
| Click to display the text | |
| [12] |
黄一,薛文超,杨晓霞.自抗扰控制:思想、理论分析及运用[C]//第29届中国控制会议论文集.北京:中国自动化学会控制理论专业委员会, 2010:29-31. Huang Y, Xue W C, Yang X X.Active disturbance rejection control:Methodology, theoretical analysis and applications[C]//Proceedings of the 29th Chinese Control Conference.Beijing:Technical Committee on Control Theory, Chinese Association of Automation, 2010:29-31(in Chinese). |
| [13] |
韩京清.自抗扰控制器及其应用[J].控制与决策, 1998, 13(1):19-23. Han J Q.Active disturbance rejection controller and its applications[J].Control and Decision, 1998, 13(1):19-23(in Chinese). |
| Cited By in Cnki (854) | |
| [14] | Gao Z Q.Active disturbance rejection control:A paradigm shift in feedback control system design[C]//Proceedings of the American Control Conference.Piscataway, NJ:IEEE Press, 2006:2399-2405. |
| Click to display the text | |
| [15] | Talbot P D, Tinling B E, Decker W A, et al.A mathematical model of a single main rotor helicopter for piloted simulation, NASA-TM-84281[R].Washington, D.C.:NASA, 1982. |
| Click to display the text | |
| [16] | Hilbert K B.A mathematical model of the UH-60 helicopter, NASA-TM-85890[R].Washington, D.C.:NASA, 1984. |
| Click to display the text | |
| [17] | Howlett J J.UH-60A black hawk engineering simulation program:Volumes I-Mathematical model, NASA-CR-166309[R].Washington, D.C.:NASA, 1981. |
| Click to display the text | |
| [18] |
吴超,谭剑锋,王浩文,等.基于GA/LM混合优化的直升机全机配平算法[J].飞行力学, 2014, 32(1):5-19. Wu C, Tan J F, Wang H W, et al.Optimal trim for helicopter based on GA and LM hybrid algorithm[J].Flight Dynamics, 2014, 32(1):5-19(in Chinese). |
| Cited By in Cnki (2) | |
| [19] | Moorhouse D, Woodcock R.US military specification MIL-F-8785C[R].Washington, D.C.:US Department of Defense, 1980. |
| [20] | Ballin M G.Validation of a real-time engineering simulation of the UH-60A helicopter, NASA-TM-88359[R].Washington, D.C.:NASA, 1987. |
| [21] | Zheng Q, Chen Z, Gao Z.A dynamic decoupling control approach and its applications to chemical processes[C]//Proceedings of the American Control Conference.Piscataway, NJ:IEEE Press, 2007:5176-5181. |
| Click to display the text | |
| [22] | Zheng Q, Gao L Q, Gao Z.On estimation of plant dynamics and disturbance from input-output data in real time[C]//Proceedings of the IEEE International Conference on Control Applications.Piscataway, NJ:IEEE Press, 2007:1167-1172. |
| Click to display the text | |
| [23] | Zheng Q, Gao L Q, Gao Z.On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics[C]//Proceedings of the 46th IEEE Conference on Decision and Control.Piscataway, NJ:IEEE Press, 2007:3501-3506. |
| Click to display the text | |
| [24] | ADS-33D-PRF.Aeronautical design standard performance specification handling qualities requirements for military rotorcraft[S].Missouri:ATCOM, 1996. |
| Click to display the text | |
| [25] | Apkarian P, Noll D.Nonsmooth H∞ synthesis[J].IEEE Transactions on Automatic Control, 2006, 51(1):71-86. |
| Click to display the text | |
| [26] | Tischler M B, Colbourne J D, Morel M R, et al.A multi-disciplinary flight control development environment and its application to a helicopter[J].Control Systems, IEEE, 1999, 19(4):22-33. |
| Click to display the text |