2. 清华信息科学与技术国家实验室(筹), 北京 100084
2. Tsinghua National Laboratory for Information Science and Technology(TNist), Beijing 100084, China
随着计算机性能的提高,计算电磁学领域在近几十年来有了很大的发展,人们越来越需要求解大规模电磁场问题.大规模电磁场问题中未知数数量多,矩阵条件数高,难以准确求解[1].同时,在一个大规模电磁场计算问题中往往涉及多种尺度的结构,难以采用单一算法同时求解[2] .由此人们发展了多种区域分解算法(Domain Decomposition Method,DDM),并在计算电磁学中进行了广泛的应用,如基于微分方程的DDM[3]、积分方程的DDM[4]等.
等效原理算法(Equivalence Principle Algorithm,EPA)是一种基于惠更斯等效原理、借鉴了区域分解思想的算法[5].目前EPA的研究方向较多.Li和Chew讨论了散射体穿过等效面时EPA的公式形式[6, 7].Yl-Oijala和Taskinen报道了一种提高等效面接近散射体时算法精度的方法T-EPA(Tangential EPA)[8],Shao等[9] 对T-EPA中求逆操作做了进一步改进,提升了其计算速度.Sun等[10]对电场积分方程中的“低频崩溃”问题进行了改进,借鉴A-EFIE(Augmented Electric Field Integral Equation)[11]的方式提出了A-EPA(Augmented EPA)方法.针对大型阵列问题,Zhang等[12]提出了PEPA(Periodic EPA)方法,利用周期性结构的特点减少EPA等效面间相互作用的计算量.Shi等[13]将EPA推广到了时域.此外,南京理工大学的杨晨[14]和西安电子科技大学的张博[15]针对EPA分别采用了快速多极子算法(Fast Multipole Algorithm,FMA)和自适应交叉近似(Adaptive Cross Approximation,ACA)进行加速.可见EPA已逐渐从理论走向实际应用.
由于EPA中涉及多次矩阵乘法与基函数变换,且每一次运算都有可能引入一定误差,对等效原理算法的误差来源进行分析就变得十分必要.本文计算了选取不同形状的等效面时其表面等效磁流的误差,并相互比较,分析误差来源.
1 算法简介 1.1 等效原理简介与符号说明EPA的基本思路基于等效原理,并可以用电磁场的表面积分形式表达.自由空间中的格林函数为
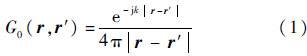
本文定义了2个积分算子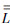 p(X)和
p(X)和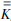 p(X)表示对一个散射体p上向量场X的某种表面积分运算:
p(X)表示对一个散射体p上向量场X的某种表面积分运算:

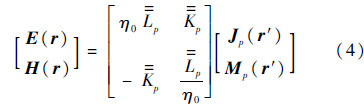
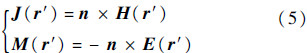
此时Sp即为等效面(Equivalence Surface,ES).
1.2 等效原理算法简介以单个理想电导体(Perfect Electric Conductor,PEC)的散射为例,介绍等效原理算法.图 1为一个PEC散射体p和等效面ES1的示意图.
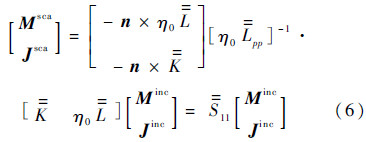
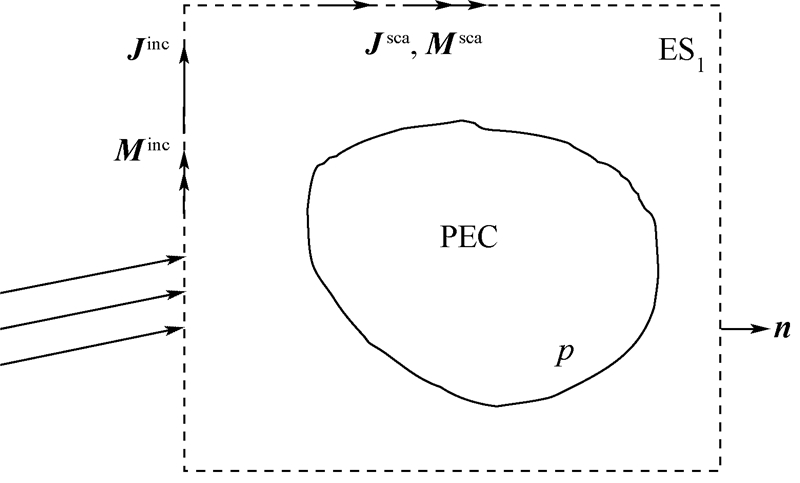 |
| Minc,Jinc—等效面上的等效入射磁流和电流;Msca,Jsca—等效面上的等效散射磁流与电流. 图 1 EPA示意图Fig. 1 An illustration of EPA |
式(6)的物理含义是ES上的等效入射磁流和电流首先通过[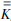 η0
η0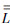 ]算子(Outside In算子)[6]向内辐射至PEC上,然后对于PEC采用电场积分方程(Electric Field Integral Equation,EFIE)得到其表面电流.
]算子(Outside In算子)[6]向内辐射至PEC上,然后对于PEC采用电场积分方程(Electric Field Integral Equation,EFIE)得到其表面电流.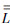 pp表示求解PEC散射体上电流的EFIE求解算子,下标pp表示
pp表示求解PEC散射体上电流的EFIE求解算子,下标pp表示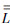 (X)算子从散射体p作用到自身.如果散射体不是PEC,只需要将求解散射体表面电流的EFIE求解算子换成相应的混合场积分方程(Combined Field Integral Equation,CFIE)算子即可.最后由[-n×η0
(X)算子从散射体p作用到自身.如果散射体不是PEC,只需要将求解散射体表面电流的EFIE求解算子换成相应的混合场积分方程(Combined Field Integral Equation,CFIE)算子即可.最后由[-n×η0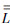 -n×
-n×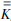 ]T算子(Inside Out算子)[6]再将PEC上的电流向外投影到等效面ES1上,得到等效散射磁流和电流.根据等效原理,该PEC对外界的辐射场与等效面上的等效磁流与电流形成的辐射场完全一致.整个过程可以用等效面ES1上的等效原理算子(Equivalence Principle Operator,EPO)[6]
]T算子(Inside Out算子)[6]再将PEC上的电流向外投影到等效面ES1上,得到等效散射磁流和电流.根据等效原理,该PEC对外界的辐射场与等效面上的等效磁流与电流形成的辐射场完全一致.整个过程可以用等效面ES1上的等效原理算子(Equivalence Principle Operator,EPO)[6]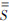 11表示.当PEC表面的未知数较多时,可以在等效面上使用较少的未知数等效原始PEC向外辐射的特性.
11表示.当PEC表面的未知数较多时,可以在等效面上使用较少的未知数等效原始PEC向外辐射的特性.
在多个散射体的情况下,第i个等效面上的等效入射电流和磁流除了有原始入射场的贡献,还有除i以外其他等效面的辐射贡献,其中第j个等效面的辐射贡献可以用传输算子(Transmission Operator,TO)[6]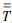 ij表示,如式(7)所示.这样可以将散射体之间未知数的相互耦合转移到等效面之间的相互耦合,可以减少计算量,改善待求解矩阵的性态.
ij表示,如式(7)所示.这样可以将散射体之间未知数的相互耦合转移到等效面之间的相互耦合,可以减少计算量,改善待求解矩阵的性态.
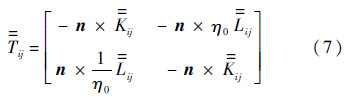
入射场的等效磁流Minc与等效电流Jinc可以投影到基函数组{f<isup>1}上,得到二组向量mincp和jincp,其分量如式(8)所示.其中脚标p表示对应的分量值是入射场在基函数组上的投影值,〈·,·〉表示向量场的内积.
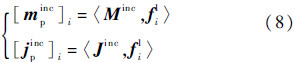
Minc和Jinc也可以用基函数组{fi1}展开,得到二组向量mcinc和jcinc向量,如式(9)所示.其中脚标c表示对应的分量值是入射场用基函数组的展开系数.
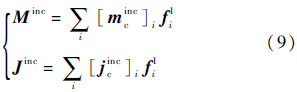
mhincc和mincp以及jcinc和jincp可以通过{fi1}的Gram矩阵[5]U1进行转换,以mcinc和mpinc为例,转换过程如式(10)、式(11)所示.
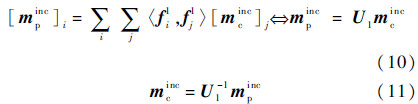
同理,可以用基函数组{f2i}展开散射等效源,得到相应的系数向量mscac和jscac:
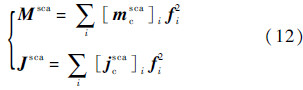
将式(6)右端的入射等效源投影到基函数组{f1i}上,可以得到矩阵方程:
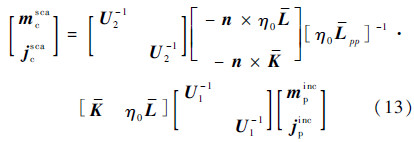
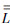 和
和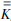 算子离散化后对应的矩阵.基函数可以采用RWG(Rao-Wilton-Glisson)函数[17]、Rooftop函数[18]等,测试基函数根据情况选择RWG或n×RWG函数.
算子离散化后对应的矩阵.基函数可以采用RWG(Rao-Wilton-Glisson)函数[17]、Rooftop函数[18]等,测试基函数根据情况选择RWG或n×RWG函数.
与直接使用EFIE算子[η0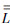 pp]-1求解散射场相比,EPA引入了两个额外的算子Outside In和Inside Out,它们都有可能带来新的误差.下面针对这两个算子进行误差分析.本文的误差用均方根误差(Root Mean Square Error,RMSE)ε衡量,对于一组准确值为{xi,0}的变量{xi},其定义为
pp]-1求解散射场相比,EPA引入了两个额外的算子Outside In和Inside Out,它们都有可能带来新的误差.下面针对这两个算子进行误差分析.本文的误差用均方根误差(Root Mean Square Error,RMSE)ε衡量,对于一组准确值为{xi,0}的变量{xi},其定义为
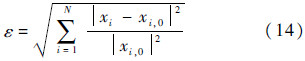
选取真空中半径r=1 m的PEC球,入射电磁波沿-x方向传播,频率100 MHz,电场极化方向为-z方向.PEC上网格尺寸为0.2 m(≈1/15λ,λ为该频率电磁波在真空中的波长).求解普通的EFIE方程,该PEC球的后向双站雷达散射截面(Radar Cross Section,RCS)在φ=0°平面内的值如图 2所示,与Mie散射的解析解[16]的均方根误差为-13.8 dB.
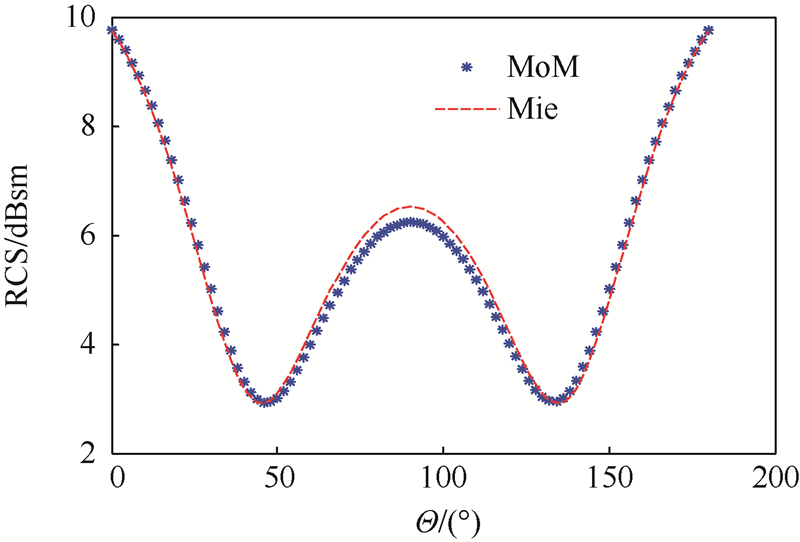 |
| 图 2 PEC球的后向RCSFig. 2 Backward RCS of PEC sphere |
对于Outside In算子,用经过[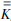 η0
η0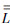 ]算子得到的入射场在散射体表面与基函数的内积,和散射体表面的入射场在散射体表面与基函数的内积比较.等效面为球形,半径为1.2 m,网格尺寸为0.3 m(≈1/10λ),大于散射体的网格.其入射场与基函数内积的均方根误差为-19.1 dB,小于原始矩量法(Method of Moment,MoM)的误差,可以接受.
]算子得到的入射场在散射体表面与基函数的内积,和散射体表面的入射场在散射体表面与基函数的内积比较.等效面为球形,半径为1.2 m,网格尺寸为0.3 m(≈1/10λ),大于散射体的网格.其入射场与基函数内积的均方根误差为-19.1 dB,小于原始矩量法(Method of Moment,MoM)的误差,可以接受.
对于Inside Out算子,比较[-n×η0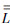 -n×
-n×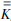 ]T中的n×
]T中的n×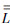 算子在等效面上投影得到的等效散射磁流与Mie散射解析解的误差.其中散射体表面电流由式(15)表示,{fi}为RWG函数.分别用RWG函数和n×RWG函数对MoM方程进行测试,如式(16)和式(17)所示.此外,从散射体向等效面辐射时也可以直接用n×
算子在等效面上投影得到的等效散射磁流与Mie散射解析解的误差.其中散射体表面电流由式(15)表示,{fi}为RWG函数.分别用RWG函数和n×RWG函数对MoM方程进行测试,如式(16)和式(17)所示.此外,从散射体向等效面辐射时也可以直接用n×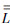 算子对散射体表面电流作用,如式(18)所示.
算子对散射体表面电流作用,如式(18)所示.
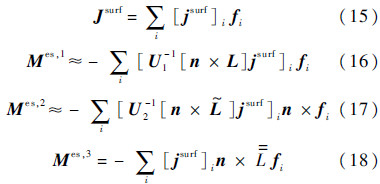
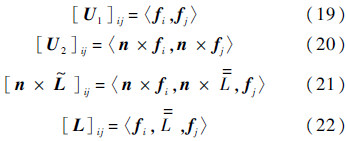
此外还采用Mie散射近场计算公式计算了从散射体辐射至等效面的等效磁流,用作等效表面磁流的精确值.下面针对不同形状的等效面计算相应的误差情况.
首先,使用立方体形状的等效面,边长从2.4 m连续变化至6 m,网格尺寸不变,均为0.3 m(≈1/10λ).均方根误差结果如图 3所示,图例中的各方法说明如表 1所示.可见随着等效面尺寸的增加,方法1的均方根误差减小,方法2和方法3的均方根误差基本不变,且使用RWG函数测试n×L(方法1)效果较方法2好.使用方法1后等效磁流误差值在立方体等效面上的分布如图 4所示,可见靠近棱边的部位误差较大.
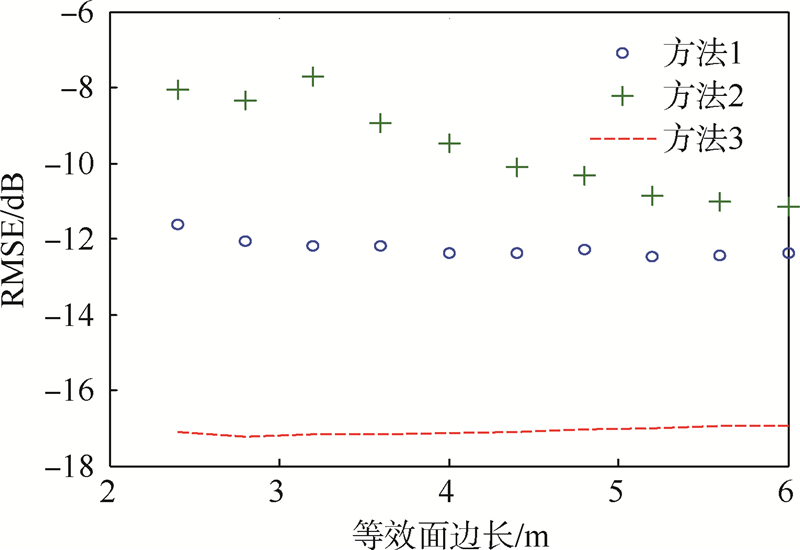 |
| 图 3 不同算法下不同尺寸立方体等效面的均方根误差Fig. 3 RMSE of cubic equivalence surfaces with different sizes under different methods |
 |
| 图 4 立方体等效面误差分布Fig. 4 Distribution of error on a cubic equivalence surface |
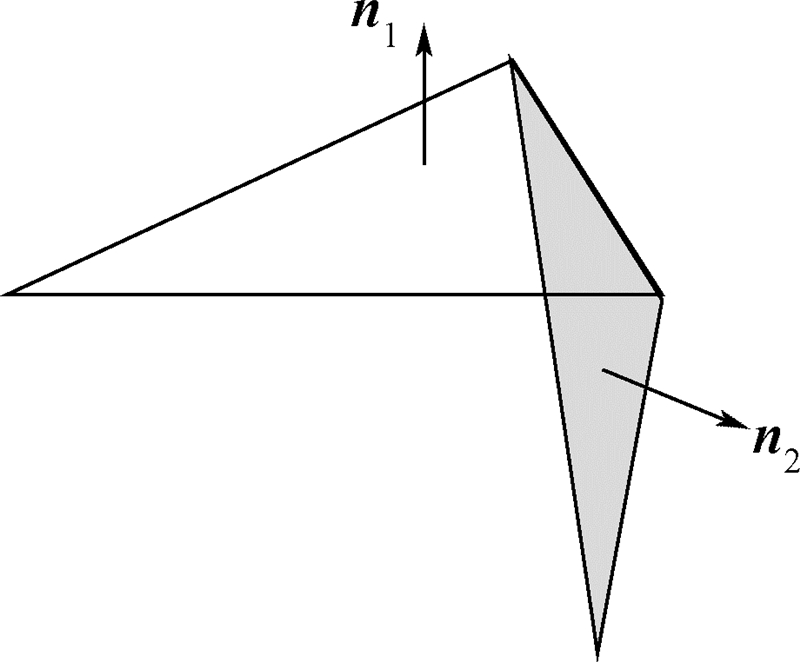
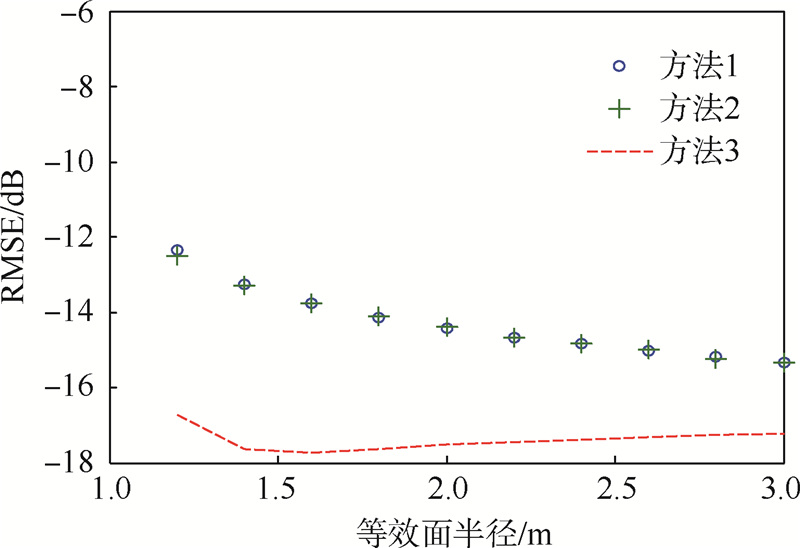
将等效面换为球形,直径也从2.4 m扫描至6 m,结果如图 5所示.与图 3相比,球形等效面上使用RWG和n×RWG函数对n×L=算子进行测试的效果基本相同,且随着等效面尺寸的增加而下降.主要原因是等效电流和等效磁流同时取决于磁场、电场和等效面的法向向量.散射体的散射场是连续的,但在立方体等效面的棱边附近,等效面表面的法向向量不连续,导致在棱边两侧的等效电流和等效磁流不连续,如图 6所示.但在球形等效面上不存在这样的问题.
 |
| 图 5 不同算法下不同尺寸球形等效面的均方根误差Fig. 5 RMSE of spherical equivalence surface with different sizes under different methods |
 |
| 图 6 一条棱边上法向向量不连续的示意图Fig. 6 Illustration of discontinuity of normal vector on an edge |
球形等效面不同位置的等效磁流误差值分布如图 7所示.与图 4相比,球形等效面上的等效磁流计算误差的分布相对均匀,主要原因是球形等效面没有棱边,不会出现立方体等效面情况下误差集中在棱边附近的情况.
 |
| 图 7 球形等效面误差分布Fig. 7 Distribution of error on a spherical equivalence surface |
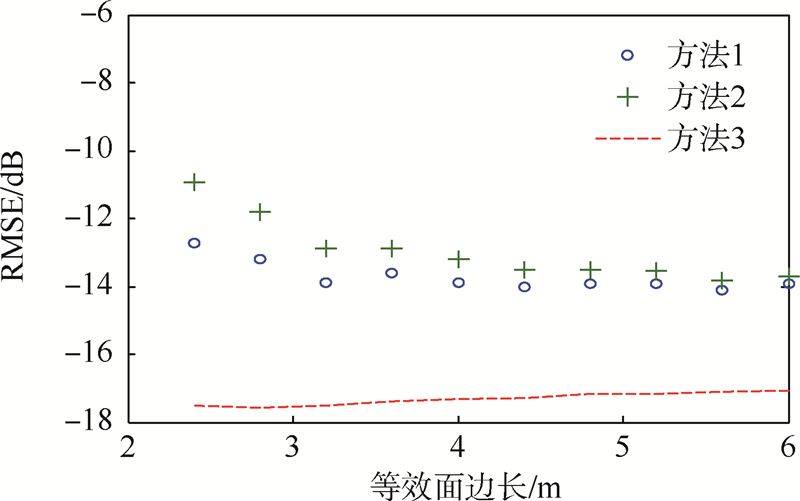
将立方体等效面的棱边做平滑处理,把立方体的棱边用光滑柱面替代、顶点用球面替代,如图 8所示,该图对应的立方体边长为6 m,柱面和球面的半径为1.5 m.随着等效面尺寸增大,均方根误差结果如图 9所示,误差分布如图 8所示.与立方体等效面的结果相比,误差有所改善,方法1基本达到了球形等效面的误差水平,但方法2没有达到.主要原因是该立方体仍然存在不完全光滑的边,而且n×RWG函数不是散度共形函数,不适合表示不光滑的等效面上的等效磁流.
 |
| 图 8 平滑立方体等效面的误差分布Fig. 8 Distribution of error on a smooth cubic equivalence surface |
 |
| 图 9 不同算法下不同尺寸平滑立方体等效面的均方根误差Fig. 9 RMSE of a smooth cubic equivalence surface with different sizes under different methods |
以上讨论了Inside Out算子的近场的误差,下文将根据方法1得到的等效面表面等效散射磁流与等效散射电流,进而计算φ=0°平面的RCS.不同形状的等效面其结果如图 10所示.它们与直接由EFIE得到的RCS的精度基本相同,说明等效面可以通过等效面上较为稀疏的网格得到与传统EFIE方法相同的精度,可以有效减小散射体之间的相互作用的计算量.
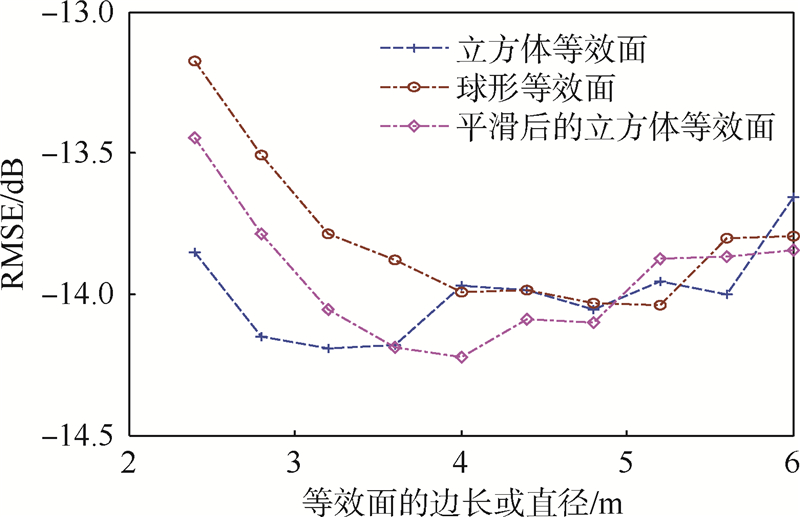 |
| 图 10 由不同等效面计算RCS的均方根误差Fig. 10 RMSE of RCS calculated from different equivalence surfaces |
通过对不同等效面的等效磁流和RCS的比较,可以得出如下结论:
1) 在相同的网格尺寸下,等效面尺寸越大,表面等效磁流的计算误差越小.
2) 等效面的棱边会增加表面等效磁流的误差.对立方体等效面适当的平滑处理可以减少误差,但难以达到球形等效面的误差水平.
3) n×RWG函数不是散度共形函数,不适合用作对等效磁流的展开.
4) 等效面可以通过更为稀疏的网格代表散射体向外辐射作用,同时保证和原先基本相同的精度,适合用作求解多尺度大规模散射问题.
实际选取等效面时除了考虑减小其表面磁流的误差外,还需要考虑一些限制.如对于天线阵列,选取立方体的等效面可以使两个相接触的表面的等效源相消[7],可以减少计算量,而球形等效面不具有这样的性质.
| [1] | Andriulli F P, Cools K, Bagci H, et al.A multiplicative Calderon preconditioner for the electric field integral equation[J].IEEE Transactions on Antennas and Propagation, 2008, 56(8):2398-2412. |
| Click to display the text | |
| [2] | Heldring A, Rius J M, Tamayo J M, et al.Multiscale compressed block decomposition for fast direct solution of method of moments linear system[J].IEEE Transactions on Antennas and Propagation, 2011, 59(2):526-536. |
| Click to display the text | |
| [3] | Li Y J, Jin J M.A new dual-primal domain decomposition approach for finite element simulation of 3-D large-scale electromagnetic problems[J].IEEE Transactions on Antennas and Propagation, 2007, 55(10):2803-2810. |
| Click to display the text | |
| [4] | Peng Z, Wang X C, Lee J F.Integral equation based domain decomposition method for solving electromagnetic wave scattering from non-penetrable objects[J].IEEE Transactions on Antennas and Propagation, 2011, 59(9):3328-3338. |
| Click to display the text | |
| [5] | Li M K, Chew W C, Jiang L J.A domain decomposition scheme based on equivalence theorem[J].Microwave and Optical Technology Letters, 2006, 48(9):1853-1857. |
| Click to display the text | |
| [6] | Li M K, Chew W C.Wave-field interaction with complex structures using equivalence principle algorithm[J].IEEE Transactions on Antennas and Propagation, 2007, 55(1):130-138. |
| Click to display the text | |
| [7] | Li M K, Chew W C.Multiscale simulation of complex structures using equivalence principle algorithm with high-order field point sampling scheme[J].IEEE Transactions on Antennas and Propagation, 2008, 56(8):2389-2397. |
| Click to display the text | |
| [8] | Ylä-Oijala P, Taskinen M.Electromagnetic scattering by large and complex structures with surface equivalence principle algorithm[J].Waves in Random and Complex Media, 2009, 19(1):105-125. |
| Click to display the text | |
| [9] | Shao H, Hu J, Guo H, et al.Fast simulation of array structures using T-EPA with hierarchical LU decomposition[J].IEEE Antennas and Wireless Propagation Letters, 2012, 11:1560-1563. |
| Click to display the text | |
| [10] | Sun L E, Chew W C, Jin J M.Augmented equivalence principle algorithm at low frequencies[J].Microwave and Optical Technology Letters, 2010, 52(10):2274-2279. |
| Click to display the text | |
| [11] | Qian Z G, Chew W C.Fast full-wave surface integral equation solver for multiscale structure modeling[J].IEEE Transactions on Antennas and Propagation, 2009, 57(11):3594-3601. |
| Click to display the text | |
| [12] | Zhang K, Ouyang J, Yang F, et al.Radiation analysis of large antenna array by using periodic equivalence principle algorithm[J].Progress in Electromagnetics Research, 2013, 136:43-59. |
| Click to display the text | |
| [13] | Shi Y, Wang J, Liang C H.A time-domain equivalence principle and its marching-on-in-degree solution[J].Microwave and Optical Technology Letters, 2014, 56(10):2415-2422. |
| Click to display the text | |
| [14] | 杨晨.基于等效原理的区域分解算法[D].南京:南京理工大学, 2013.Yang C.Domain decomposition method based on equivalence principle[D].Nanjing:Nanjing University of Science and Technology, 2013(in Chinese). |
| Cited By in Cnki (1) | |
| [15] | 张博.等效原理算法及其结合快速算法分析目标的电磁散射[D].西安:西安电子科技大学, 2013.Zhang B.Scattering analysis of target using equivalent principle algorithm and its fast algorithm[D].Xi'an:Xidian University, 2013(in Chinese). |
| Cited By in Cnki | |
| [16] | Chew W C.Waves and fields in inhomogeneous media[M].Piscataway, NJ:IEEE Press, 1995:29, 186. |
| [17] | Rao S M, Wilton D, Glisson A W.Electromagnetic scattering by surfaces of arbitrary shape[J].IEEE Transactions on Antennas and Propagation, 1982, 30(3):409-418. |
| Click to display the text | |
| [18] | Jin J M.Theory and computation of electromagnetic fields[M].Hoboken, New Jersey:John Wiley & Sons, 2011:439-440. |



