2. 中国民航大学 中欧航空工程师学院, 天津 300300
2. Sino-European Institute of Aviation Engineering, Civil Aviation University of China, Tianjin 300300, China
航空发动机的风险水平指在规定的时间内、正常飞行的条件下,航空发动机出现故障的概率或次数[1].故障风险预测方法能够给出航空发动机在未来一段时间周期内可能发生故障的次数.航空运营企业为了保证飞机运行的可靠性,需要计划好发动机维修,并储备相应数量的需备件,这就需要对发动机的故障风险水平做出预测,估计发动机在未来一段时间内各部件及发动机系统出现故障的次数,从而为生产或运营计划做出安排.
航空发动机部件多,结构复杂,不同部件都有各自的故障概率分布.经过多年发展,航空发动机部件故障概率的分析方法有很多[2, 3].其中,经典的解析方法虽然能够给出单个部件统计特性的精确表达式,但是用于确定多部件组成的复杂系统的故障风险等可靠性参数是十分困难的.而其他系统分析方法,如故障树分析法、马尔可夫状态转移法等,其问题求解的规模往往会随着部件数目的增多而呈指数量级增大[4, 5],且对所求解的系统往往有一定限制(如部件故障概率分布形式等).蒙特卡罗方法作为一种随机模拟方法,通过对模型或系统的观察或抽样试验来计算所求参数的统计特征,能够很好地避免以上问题. 1 蒙特卡罗方法
蒙特卡罗方法的主要步骤[6]包括:针对具体问题构造相应的概率过程;实现已知概率分布的随机抽样;利用随机抽样的结果计算具体的估计量. 1.1 构造概率过程
构造概率过程即找到具体问题所服从的概率分布,如二项分布、指数分布、正态分布等.准确描述问题的概率过程是蒙特卡罗求解方法的关键,整个随机模拟过程都是建立在已知的概率分布之上.如何确定问题所服从的概率分布,这需要根据已有的数据并结合相应的数据处理方法来确定. 1.2 随机抽样与统计
构造完概率过程后,就知道了系统各个部分所服从的概率分布,如一辆汽车中仪表盘等电子元器件寿命可能服从指数分布,发动机故障时间可能服从威布尔分布等.在已知概率分布的基础上,产生满足相应分布的随机变量即为随机抽样过程.随机抽样的核心在于随机数的生成,常用的方法有工程上的物理方法和数学公式递推法.工程上的物理方法无法重复便捷地生成随机数,且价格昂贵.数学递推公式法利用计算机就可重复产生大量的随机数,虽然无法做到真正意义上的随机性,但只要满足相应的随机数检验,即可满足大部分要求[7].
蒙特卡罗模拟方法能否得到好的结果关键在于整个随机过程的构造和计算过程中随机数的性质.在随机抽样的基础上,根据所求解的问题,对随机抽样过程中产生的数据进行记录、统计,进而确定问题的估计量,得到问题的解. 2 故障风险预测算法 2.1 故障概率模型
在航空发动机故障数据处理中,威布尔分布是最常见的,且与数据符合程度相对较好的一种分布[8].航空发动机是一种高可靠性的产品,通常只有小样本的故障数据.威布尔分析在处理小样本数据时,与其他分析方法相比通常都具有较好的效果[9, 10].因此,在航空发动机故障风险预测中,本文采用了威布尔分布模型.
威布尔累积概率分布函数为
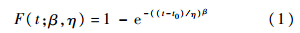
对于小样本航空发动机故障数据,为了得到合适的尺度参数和形状参数,采用中位秩回归参数估计法[11].
1) 将故障时间数据T=[T1 T2 … Tn]T从小到大排列,并利用式(2)计算各个数据的中位秩,当故障时间数据中存在删失数据时,需利用式(3)调整数据排序值.
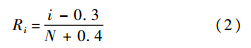
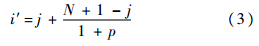
2) 计算故障时间的自然对数,记为Y=ln T,并令
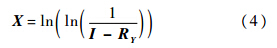
3) 计算方程y=A+Bx的最小均方估计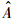 和
和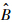 ,满足式(5)和式(6).
,满足式(5)和式(6).

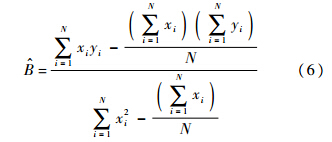
4) 求解中位秩回归参数,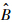 和
和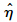 为威布尔参数β,η的估计值.
为威布尔参数β,η的估计值.

满足威布尔分布的随机数生成算法有很多,反变换法是其中一种便捷、有效的方法[12, 13].设需产生分布函数F(x)的连续随机数x,若已有[0,1]区间均匀随机数r,则产生x的反变换公式[14]为

则威布尔的反变换公式为
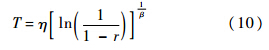
反变换法的关键在于[0,1]区间上高品质的均匀随机数.采用目前广泛使用的乘同余组合发生器来产生[0,1]区间上的均匀随机数.递推公式[15]为
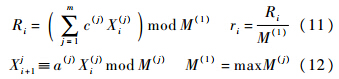
选取组合数m=2,且令
M(1)=2 146 058 219 a(1)=43 465 c(1)=1
M(2)=2 145 434 063 a(2)=45 271 c(2)=-1
设发动机有n种故障模式,记为F1,F2,…,Fn.这n种故障模式相互独立,均服从威布尔分布,参数记为(η1,β1),(η2,β2),…,(ηn,βn),故障时间抽样为
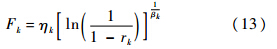
假定发动机定期检查时间为T,故障修复后,发动机使用时间重新计,累积到时间T时,再做下次定检,则蒙特卡罗模拟运行流程如图 1所示.
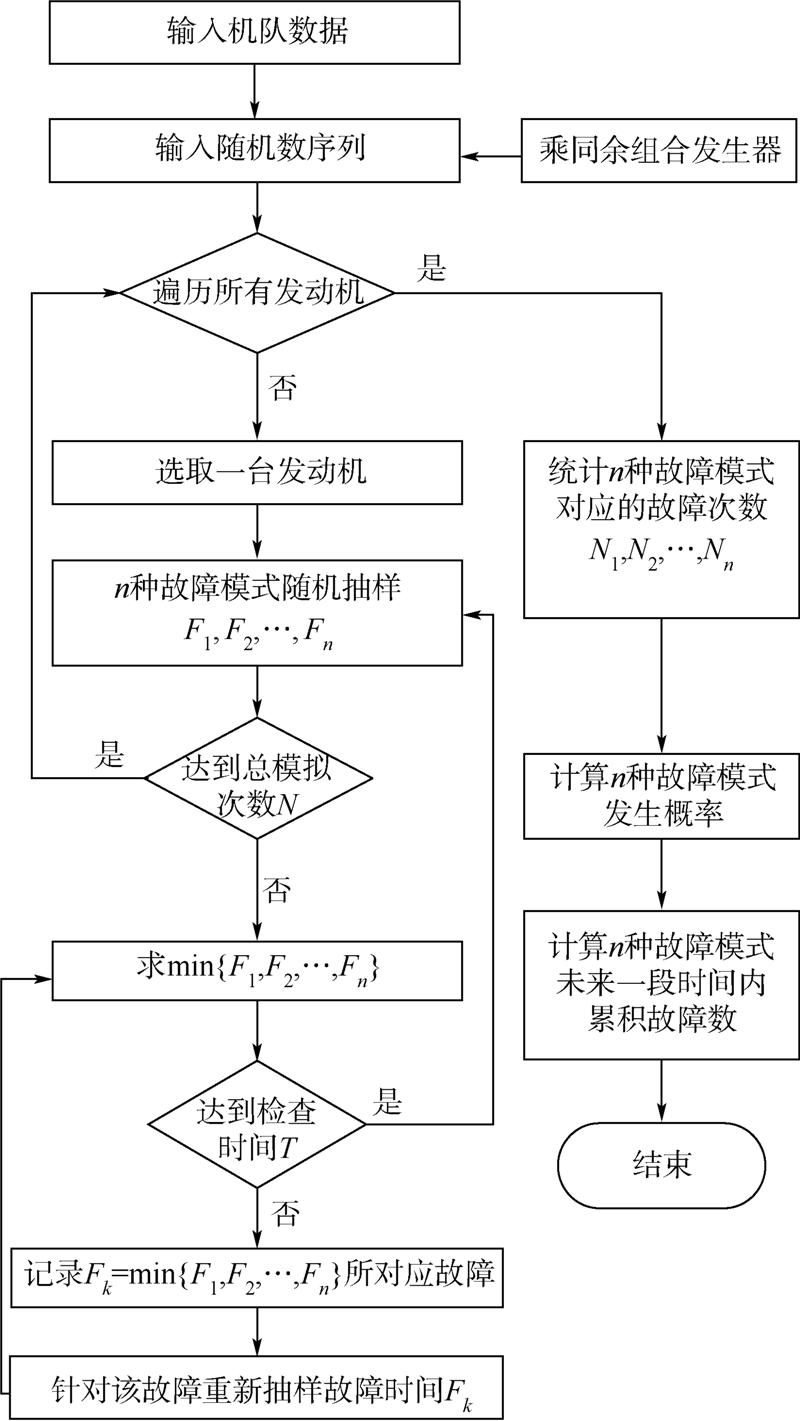 |
| 图 1 蒙特卡罗模拟流程Fig. 1 Monte Carlo simulation process |
由图 1可知,模拟的基本步骤如下:
1) 输入机队的原始数据,包括机队总数,使用率,机队年龄分布;
2) 利用乘同余组合发生器构建[0,1]区间均匀随机数表;
3) 针对每台发动机,从随机数表中顺序选取随机数,利用式(13)计算各个故障模式的随机故障时间F1,F2,…,Fn,首次故障时间需大于发动机的已安全运行时间,否则需重新产生一组随机故障时间,直到均大于发动机已安全运行时间;
4) 判断min{F1,F2,…,Fn}是否小于定期检查时间T,若是,则记录该故障Fk,该故障模式发生次数累加1;
5) 针对k故障模式,重新抽样故障时间Fk;
6) 重复步骤4)和步骤5),直到min{F1,F2,…,Fn}超过发动机定期检查时间T,则一次模拟结束;
7) 遍历机队内所有发动机,每台发动机均进行N次模拟,并记录结果;
8) 计算发动机各个故障模式发生的概率;
9) 结合机队原始数据,计算机队未来一段时间内发动机各个故障模式可能发生的次数. 3 算例及结果分析 3.1 算例描述
为了验证该模型的准确性与适用性,本文采用了某发动机公司手册中的数据作为输入条件,利用上述故障风险预测算法进行模拟仿真,并将结果与发动机公司给出的软件仿真结果进行分析对比.手册中提供了某喷气式发动机4种相互独立的故障模式:F1表示过热,F2表示叶片裂纹,F3表示油管裂纹,F4表示燃烧室裂纹.4种故障模式均服从不同参数的威布尔分布,具体参数见表 1.同时,发动机的定期检查时间为1 000 h,整个机队发动机运行时间分布如图 2所示.假定发动机使用率为25 h/月.
| 故障模式 | η | β |
| F1 | 10 193 | 2.09 |
| F2 | 2 336 | 4.57 |
| F3 | 12 050 | 1.885 |
| F4 | 3 149 | 4.03 |
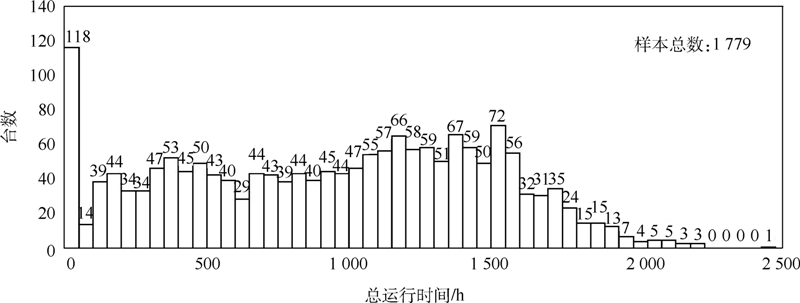 |
| 图 2 机队发动机运行时间分布Fig. 2 Operation time distribution of engine fleet |
针对初始时间为0的发动机,详细阐述蒙特卡罗风险预测方法,模拟流程见图 3.
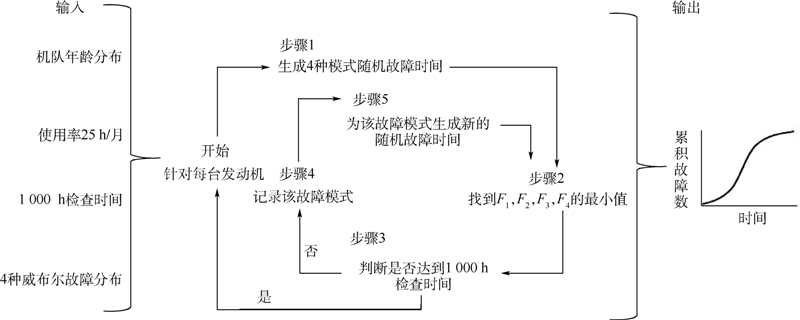 |
| 图 3 模拟流程Fig. 3 Simulation process |
1) 为4种模式生成随机故障时间.利用随机数表,顺序选取前4个[0,1]区间上的随机数:0.007,0.028,0.517,0.603.根据式(13),则有:F1=951 h,F2=1 072 h,F3=10 180 h,F4=3 088 h.
2) 4种故障模式中,最小的故障时间为951 h,并未达到定期检查时间1 000 h.
3) 最先发生的为F1故障,记录该故障发生时间为951 h,相当于在未来第38个月发生故障.从随机数表中选取下一个随机数0.442,为F1故障重新生成随机故障时间,F1=8 827 h.此时,min{F1,F2,F3,F4}已超过定期检查时间1 000 h.至此,一次模拟结束.
针对每台发动机重复模拟N次,并遍历所有发动机.根据大数定理,则发动机故障发生概率近似为
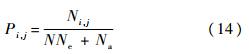
则发动机故障风险预测结果为

发动机一年内的故障风险预测结果见表 2,某发动机公司提供的内部软件预测结果见表 3,图 4给出了12月份发动机故障次数的收敛结果.
| 月份 | 故障次数 | |||
| F1 | F2 | F3 | F4 | |
| 1月 | 0 | 0 | 0 | 0 |
| 2月 | 0.203 815 | 0.461 832 | 0.240 431 | 0.221 532 |
| 3月 | 0.401 265 | 0.891 837 | 0.484 208 | 0.429 415 |
| 4月 | 0.609 607 | 1.382 214 | 0.730 675 | 0.666 959 |
| 5月 | 0.813 159 | 1.833 612 | 0.976 881 | 0.890 197 |
| 6月 | 1.036 660 | 2.343 870 | 1.235 160 | 1.136 468 |
| 7月 | 1.249 202 | 2.830 047 | 1.492 061 | 1.371 846 |
| 8月 | 1.475 197 | 3.382 893 | 1.755 327 | 1.635 703 |
| 9月 | 1.696 138 | 3.896 892 | 2.008 816 | 1.895 163 |
| 10月 | 1.927 382 | 4.476 445 | 2.270 442 | 2.178 049 |
| 11月 | 2.146 355 | 5.034 475 | 2.532 921 | 2.434 819 |
| 12月 | 2.376 549 | 5.657 666 | 2.801 109 | 2.729 058 |
| 月份 | 故障次数 | |||
| F1 | F2 | F3 | F4 | |
| 1月 | 0 | 0 | 0 | 0 |
| 2月 | 0.17 | 0.33 | 0.21 | 0.17 |
| 3月 | 0.38 | 0.67 | 0.47 | 0.34 |
| 4月 | 0.60 | 1.15 | 0.74 | 0.58 |
| 5月 | 0.78 | 1.47 | 0.95 | 0.74 |
| 6月 | 0.92 | 1.71 | 1.13 | 0.87 |
| 7月 | 1.22 | 2.27 | 1.49 | 1.15 |
| 8月 | 1.46 | 2.81 | 1.77 | 1.41 |
| 9月 | 1.66 | 3.16 | 2.02 | 1.60 |
| 10月 | 1.95 | 3.90 | 2.36 | 1.95 |
| 11月 | 2.07 | 4.03 | 2.51 | 2.03 |
| 12月 | 2.38 | 4.90 | 2.87 | 2.45 |
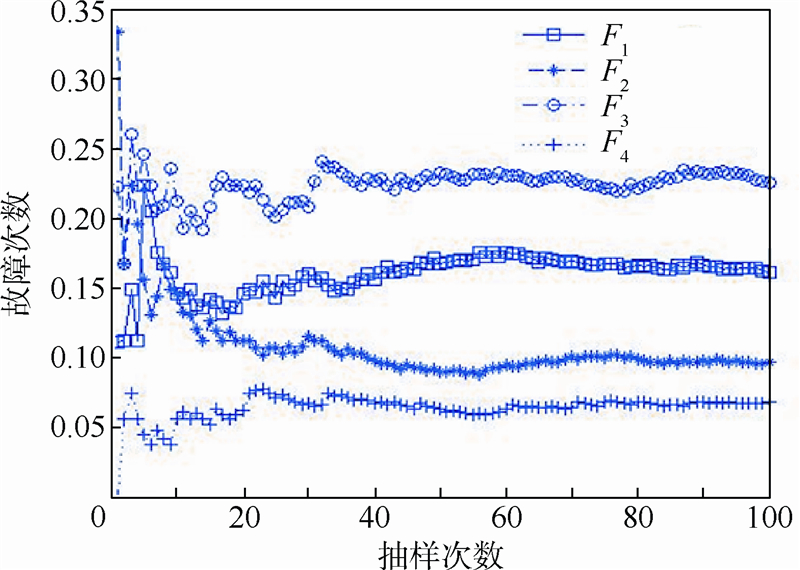 |
| 图 4 12月份发动机故障次数收敛结果Fig. 4 Convergence results of engine failure number on December |
在模拟过程中,为了得到稳定的结果,需要实时观察模拟输出的数值,以便确定输出结果是否稳定.以12月份发动机的故障次数预测结果为例,每10 000次输出一次模拟数值,并做100次抽样,则总模拟次数为106.由图 4可知,最终结果已收敛.一般来说,模拟次数越大,预测结果越逼近真实情况.在试验过程中,通过对比总模拟次数为106,107和108时的收敛图形,发现结果差别不大.因此,总模拟次数设定为106已满足收敛性要求.同时,由表 2和表 3可以看出,机队内发动机一年内各部件累积故障次数的预测结果与发动机公司提供的数据相差不大,故障总次数仅相差0.97.预测结果准确,验证了该算法的有效性与适用性. 4 结 论
1) 在确定了失效分布规律后,利用蒙特卡罗模拟算法进行仿真,能够比较准确地估算出整个机队发动机在未来不同时间段内的故障风险水平,从而为发动机维修管理提供可靠性指标参考;
2) 蒙特卡罗模拟是多故障模式下风险预测的一个有效方法,并且在多故障模式下,该算法不但可以预测机队整体风险水平,而且还可确定何种故障模式最易发生,从而可以有针对性地对该故障制定相应的改进措施,降低机队的故障风险;
3) 当某个易发故障得到改进后,可重新进行仿真模拟来找到下一个易发故障,不断迭代,从而实现对机队内发动机的动态管理.
致谢 中国民航大学郭庆副教授提供了某发动机厂商的技术资料,并为文章写作提出了建设性意见,在此表示感谢!
| [1] | 赵宇. 可靠性数据分析[M].北京:国防工业出版社,2011:14-20. Zhao Y.Data analysis of reliability[M].Beijing:National Defense Industry Press,2011:14-20(in Chinese). |
| [2] | 杨宇航, 冯允成.基于仿真的复杂系统可靠性、可用性和MTBF评估文献综述[J].系统工程理论与实践,2003,42(2):80-85. Yang Y H,Feng Y C.Survey of reliability and availability evaluation of complex system using Monte Carlo techniques[J].Systems Engineering-Theory & Practice,2003,42(2):80-85(in Chinese). |
| Cited By in Cnki (22) | |
| [3] | 刘晓平, 唐益明,郑利平.复杂系统与复杂系统仿真研究综述[J].系统仿真学报,2008,20(23):6303-6315. Liu X P,Tang Y M,Zheng L P.Survey of complex system and complex system simulation[J].Journal of System Simulation,2008,20(23):6303-6315(in Chinese). |
| Cited By in Cnki (67) | |
| [4] | 邵伟. 蒙特卡洛方法及在一些统计模型中的应用[D].济南:山东大学,2012. Shao W.Monte Carlo methods theory and their applications in some statistical model[D].Jinan:Shandong University,2012(in Chinese). |
| Cited By in Cnki (9) | |
| [5] | 袁明伟. 复杂系统可靠性分析[D].马鞍山:安徽工业大学,2013. Yuan M W.Reliability analysis of complex system[D].Maanshan:Anhui University of Technology,2013(in Chinese). |
| Cited By in Cnki | |
| [6] | Dickman B H, Gilman M J.Technical note Monte Carlo optimization[J].Journal of Optimization Theory and Applications,1989,60(1):149-157. |
| Click to display the text | |
| [7] | 周文彬. 组合式伪随机数发生器的研究与设计[D].哈尔滨:哈尔滨工程大学,2013. Zhou W B.Design and research of the combined pseudo-random number generator[D].Harbin:Harbin Engineering University,2013(in Chinese). |
| Cited By in Cnki | |
| [8] | Baumshtein M V, Prokopenko A V,Ezhov V N.Probabilistic prediction of the fatigue life of gas-turbine engine compressor blades under two-level programmed loading[J].Strength of Materials,1985,17(5):587-592. |
| Click to display the text | |
| [9] | Nee A Y C, Song B,Ong S K.Re-engineering manufacturing for sustainability[M].Singapore:Springer Singapore,2013:699-703. |
| [10] | Saralees N, Samuel K.Strength modeling using Weibull distributions[J].Journal of Mechanical Science and Technology,2008,22(7):1247-1254. |
| Click to display the text | |
| [11] | 麻晓敏,张士杰, 胡丽琴,等.可靠性数据威布尔分析中秩评定算法改进研究[J].核科学与工程,2007,27(2):152-155. Ma X M,Zhang S J,Hu L Q,et al.An improved rank assessment method for weibull analysis of reliability data[J].Nuclear Science and Engineering,2007,27(2):152-155(in Chinese). |
| Cited By in Cnki (19) | |
| [12] | Yadolah D. The concise encyclopedia of statistics[M].New York:Springer New York,2008:446-447. |
| [13] | Johnson G E. Constructions of particular random processes[J].Proceedings of the IEEE,1994,82(2):270-285. |
| Click to display the text | |
| [14] | 金畅. 蒙特卡罗方法中随机数发生器和随机抽样方法的研究[D].大连:大连理工大学,2005. Jin C.Study on random number generator and random sampling in Monte Carlo method[D].Dalian:Dalian University of Technology,2005(in Chinese). |
| Cited By in Cnki (19) | |
| [15] | 杨自强,魏公毅. 常见随机数发生器的缺陷及组合随机数发生器的理论与实践[J].数理统计与管理,2001,20(1):45-51. Yang Z Q,Wei G Y.Drawbacks in classical random number generators-theory and practice of combined generator[J].Journal of Applied Statistics and Management,2001,20(1):45-51(in Chinese). |
| Cited By in Cnki (77) |



