四杆、六杆和八杆机构五位置运动生成的综合问题已经得到解决[1,2,3,4,5,6].五位置综合得到的有限机构如果性能上不满足要求也没有其他选择.而四位置综合可以得到无穷多解,为设计者提供了更多选择,同时采用现代设计方法进行优选,最终可以得到满足多种性能要求的最优机构.因此认为,五位置综合问题的解决具有重要的理论意义,而四位置综合问题的解决更具有应用价值和实际意义.难点在于采用何种理论与方法在无穷多机构中得到机构的可行解域.
对于四位置运动生成的综合问题大都应用布尔梅斯特理论.对于六杆机构四位置运动生成问题通常所给定的是两个连杆的4个位置,有时也给定包括连架杆的4个位置,因此得到的曲线不只是圆点和圆心的分布曲线——布氏曲线,还有能表示一般情况下的解曲线,研究表明该曲线也为与布氏曲线相似的三次曲线,本文称为广义布氏曲线.本文将布氏曲线和广义布氏曲线统称为解曲线.本文在文献[7,8,9]基础上,把解域综合方法推广应用于Stephenson-Ⅱ机构.
为了建立可行解域,判断机构是否存在运动缺陷是不可少的一步.运动缺陷包括回路、分支和顺序缺陷.回路缺陷是指机构不得不进行重新装配才能通过给定的全部位置.分支缺陷是指机构在通过给定的全部位置的过程中出现死点(奇异位形).目前,虽然已有较多文献对机构运动缺陷的相关问题进行了说明,但是并没有完全解决机构运动缺陷判断问题.如文献[10]通过建立函数判别式求解出六杆机构奇异位形和机构运动范围.文献[11]利用JRS(Joint Rotation Space)方法判断六杆机构和齿轮五杆机构是否存在曲柄.在文献[12]中提出了将Stephenson-Ⅲ型六杆机构分解为四杆机构和一个Ⅱ级杆组,然后求解其运动区域的方法.文献[13]提出了八杆机构运动范围的函数判别式,但是该判别式仅对至少有一个四杆环路并且不包含六杆环路的八杆机构有效.Mirth等[14]利用四杆机构连杆曲线和Ⅱ级杆组运动范围判断给定四位置的Stephenson型六杆机构是否存在回路缺陷问题,并应用该方法得出了布氏曲线上无回路缺陷区段.本文针对机构运动缺陷判断问题,提出了雅可比矩阵行列式值的符号与运动连续性条件相结合的方法.该方法简单易行,并且能很好地解决机构运动缺陷判定问题,为建立可行解域奠定了基础.
1 解曲线方程的推导
假设有两连杆平面π1和π2,如图 1所示,其位置由平面上的一点b(m)和任选的一条直线blb(mlm)的方位角来确定.两连杆平面在第1位置时分别用π11和π21表示,其上b点为b1(xb1,yb1),m点为m1(xm1,ym1),b1lb1直线的方位角为α1,m1lm1直线的方位角为β1.两连杆平面在第i(i=2,3,4)位置时分别用π1i和π2i表示,其上b点为bi(xbi,ybi),m点为mi(xmi,ymi),bilbi直线的方位角为αi,milmi直线的方位角为βi.当连杆平面π1和π2分别从位置1到位置i(i=2,3,4)时,确定平面π1和π2上可以作为铰链的点B和M.其中连杆平面π1和π2分别从位置1到位置i的位移矩阵为[D11i]和[D21i][15].设待求第1位置的铰链点B和M矢量分别为B1=(xB1,yB1)T和M1=(xM1,yM1)T,第i位置的铰链点B和M矢量分别为Bi=(xBi,yBi)T和Mi=(xMi,yMi)T,则有
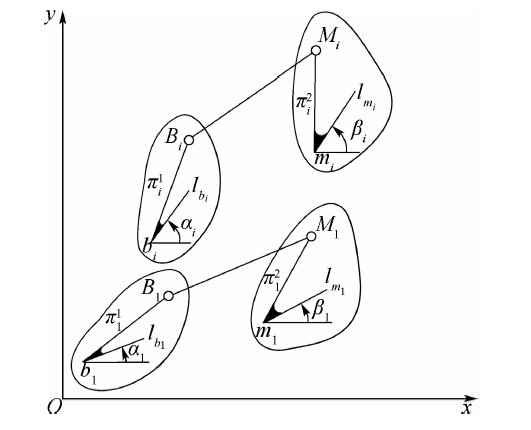 |
| 图 1 刚体平面运动示意图Fig 1 Diagram of rigid body planar motion |
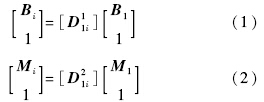
根据杆长不变条件,有约束方程:
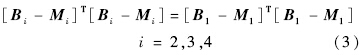
将式(1)和式(2)代入式(3)中,整理得
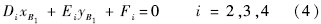
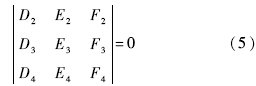
整理上式可得到关于xM1和yM1的三次方程:
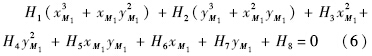
通过求解式(6)得到点M在第1位置坐标值,将其代入式(4)可以求出点B在第1位置坐标值.因点M为π2上的点,故将该曲线称为解曲线π1π2-π2,同样可以得到另一条解曲线π1π2-π1,这两条解曲线上的点具有一一对应关系.如果平面π1(或π2)为固定平面,则其对应的位移矩阵为单位矩阵,推导得到的解曲线为布氏曲线.而当两平面都不是固定平面时,则得到的解曲线为广义布氏曲线. 2 六杆机构四位置运动生成
为综合得到如图 2所示六杆机构,本文参照文献[5],给定如图 3所示3R开链的四位置参数.即已知3R开链的固定铰链点a0的坐标(a0x,a0y),动铰链点a,b在4个位置的坐标(aix,aiy),(bix,biy)(i=1,2,3,4)(或构件1,2的长度以及4个方位角θ1i,θ2i),末端执行件3上的一点p在4个位置的坐标p(pix,piy)(或点p到铰链点b的长度以及构件3的方位角θ3i).
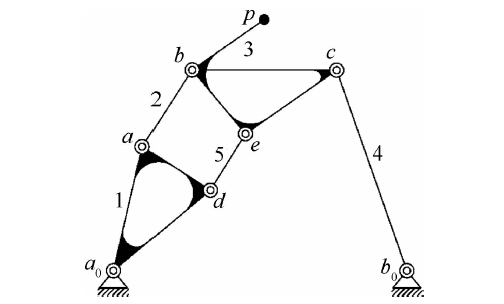 |
| 图 2 六杆机构示意图 Fig 2 Diagram of a six-bar linkage |
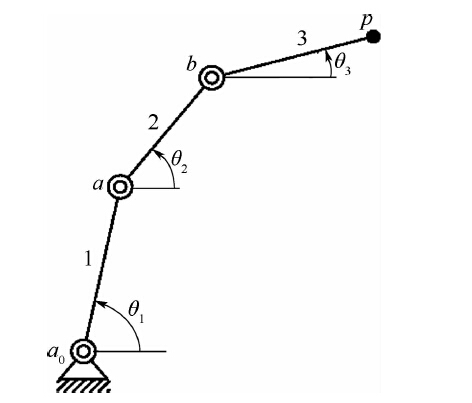 |
| 图 3 3R开链 Fig. 3 Diagram of a 3R open chain |
根据上节内容,综合构件4时因其连接机架0和构件3,故可以分别得到关于铰链点b0和c的解曲线03-0和03-3.综合构件5时分别得到关于铰链点d和e坐标的解曲线13-1和13-3,如图 4所示.
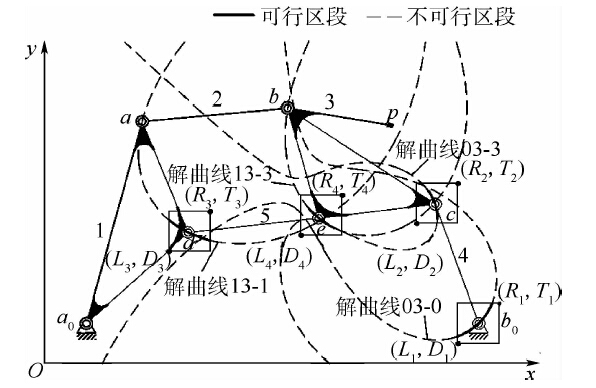 |
| 图 4 解曲线和机构Fig. 4 Solution curves and six-bar linkage |
建立解域的步骤如下:①求出关于铰链点b0和d的解曲线方程,方程形式如式(6).将x作为已知量,令x以步长Δx在其铰链点限定范围内连续取值,则可得到关于y的三次方程,该方程可能存在一个实根(有2个重根)或3个实根(无重根).②参考文献[7]中的曲线分段方法将解曲线分为区段1,2,3.③建立可行区段.如果解曲线03-0上一点满足铰链点b0的限定条件,且03-3上与之对应的点满足铰链点c的限定条件,由这样的点组成的曲线段称为可行区段,如图 4中铰链点b0限定范围内的实线段.同理求得其他解曲线的可行区段.④将解曲线03-0和13-1的可行区段中所包含的各区段(区段1,2,3)依次排列,向水平直线进行映射,而后取b0,d的x坐标值为坐标轴建立解域.因为解域内任一点都表示铰链点b0,d的x坐标值,根据第1节内容可以求得相应的y坐标值及其对应铰链点c和e的坐标值,所以解域内任意一点都对应着一个六杆机构.根据上述步骤得到的解域中的六杆机构可能在通过给定4个位置时出现运动缺陷,故需要通过下一节介绍的机构运动缺陷判定方法将存在运动缺陷的机构从解域中剔除.最后根据实际工程需要建立和施加约束条件,例如杆长比,最长、最短杆的杆长限定,传动角的限定等,进一步剔除解域中不满足要求的机构.限于篇幅,本文在综合示例中只附加杆长比r的约束条件,即在如图 5所示的六杆机构中,所标注的尺寸l1~l9和机架长度中最小值与最大值之比.将小于杆长比的机构从解域中剔除,形成没有运动缺陷且满足给定杆长比的可行解域.
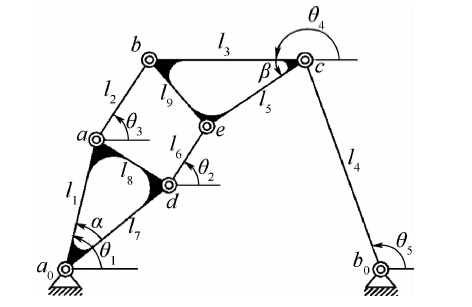 |
| 图 5 六杆机构参数示图Fig. 5 Parameters for six-bar linkage |
对图 5所示的六杆机构进行位置分析,可以得到两个矢量方程:
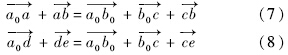
将上述式子分别向x和y轴投影并整理,得
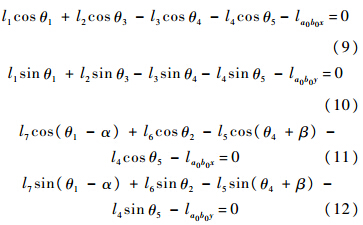
其中,la0b0x=b0x-a0x,la0b0y=b0y-a0y,(a0x,a0y)和(b0x,b0y)分别为固定铰链点a0和b0的坐标.
联立式(9)与式(10)消去θ3,联立式(11)与式(12)消去θ2,得

联立式(13)和式(14),利用Sylvester结式消元法消去θ4,得到关于θ5的方程后,令tan(θ5/2)=t5,根据半角公式,有sinθ5=2t5/(1+t25)和cosθ5=(1-t25)/(1+t25),最终得到关于t5的六次方程:
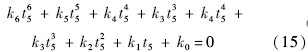
将式(9)~式(12)分别对θ2,θ3,θ4,θ5求导,整理得雅可比矩阵行列式:
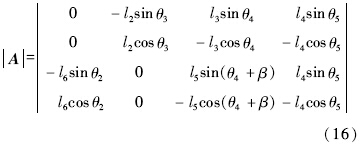

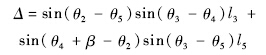
当Δ=0时机构处于奇异位形(死点),故当机构在给定位置对应的Δ值的符号不同时,机构将存在运动缺陷.但当给定位置对应的Δ值的符号相同时,机构也可能会存在运动缺陷,接下来通过表 1和图 6来进行说明.表 1给出了图 2所示六杆机构在两个位置的参数,固定铰链点a0和b0的坐标分别为(0,0)和(59.8273,0).图 6是上述六杆机构在可运动范围内的Δ曲线.Δ1和Δ2分别为给定位置1和位置2的Δ值.
| 六杆机构参数 | 位置1 | 位置2 |
| θ1/(°) | 10.00 | 50.00 |
| a | (26.78,4.72) | (17.48,20.83) |
| b | (32.17,-15.26) | (35.04,31.78) |
| c | (50.02,-23.49) | (53.29,24.47) |
| d | (21.29,-4.22) | (19.02,10.45) |
| e | (37.70,-23.82) | (41.01,23.51) |
| p | (43.58,-0.98) | (45.73,46.63) |
| Δ值 | 7.51422 | 9.94004 |
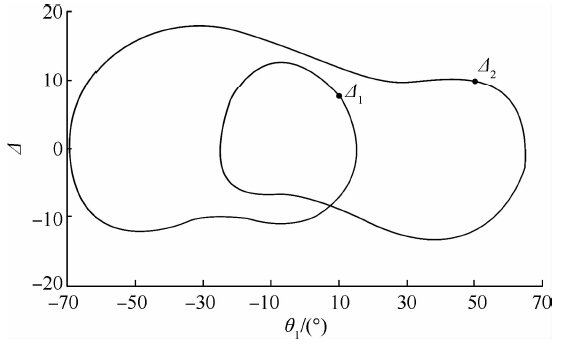 |
| 图 6 Δ随输入角变化的曲线图Fig. 6 Δ changes with the input angle |
六杆机构虽然在位置1和位置2所对应的Δ值符号相同,但从图 6的曲线可以看出,原动件在给定的运动范围内(在此说明示例中原动件的运动范围是10°~50°)不能从位置1连续运动到位置2.由此可知在位置1到位置2间存在分支缺陷.此时出现雅可比矩阵值符号判断失效,因此需要进一步根据机构的运动连续性来判断机构是否存在运动缺陷.当机构给定初始位置装配构型而后进行连续性运动(输入角连续变化),给定一输入角进行位置分析,可能得到多组装配构型,但只有一组装配构型符合连续运动要求,本文将此组装配构型称为实际装配构型.归纳总结机构运动缺陷判断步骤如下.
第1步 计算给定4个位置的Δ值,Δ值符号不同则存在运动缺陷,相同则进行第2步判断.
第2步 输入角从起始位置1按适当步长连续变化到位置2对应的输入角.如果出现以下情况则认为存在运动缺陷:①给定一输入角进行位置分析,如果无解则认为机构存在运动缺陷.②给定一输入角进行位置分析,如果得到多组装配构型,则根据机构运动的连续性,判断出与输入角对应的实际装配构型.求出实际装配构型所对应的Δ值,如果该Δ值的符号与位置1处的不同则机构认为存在运动缺陷.③当机构输入角等于给定位置2输入角时,求得的实际装配构型的铰链点坐标与给定位置2铰链点坐标不同,则认为机构存在运动缺陷.如果位置1到位置2区间不存在运动缺陷则根据第2步依次判断剩下的两个区间. 5 综合示例
综合如图 2所示的六杆机构,给定参数点a0坐标(0,0)以及表 2和表 3.
| 位置 | a | b | p |
| 1 | (13.5108,50.4228) | (48.7123,53.7165) | (78.5419,59.6493) |
| 2 | (26.1008,45.2079) | (56.5364,63.1988) | (86.7112,59.3935) |
| 3 | (36.9121,36.9121) | (65.6906,57.4497) | (87.78,36.5438) |
| 4 | (45.2079,26.1008) | (79.0142,36.4511) | (91.3807,8.66497) |
| 铰链点 | b0 | c | d | e |
| 限定范围 | (55,-5) | (55,15) | (10,17) | (45,24) |
| (98,42) | (88,45) | (80,46) | (95,50) |
按照上文所述的综合方法,综合杆b0c时,先得到关于铰链点b0和c的解曲线03-0和03-3.再根据铰链点b0和c的限定范围求解出解曲线的可行区段,如图 7所示的限定框中的实线段.
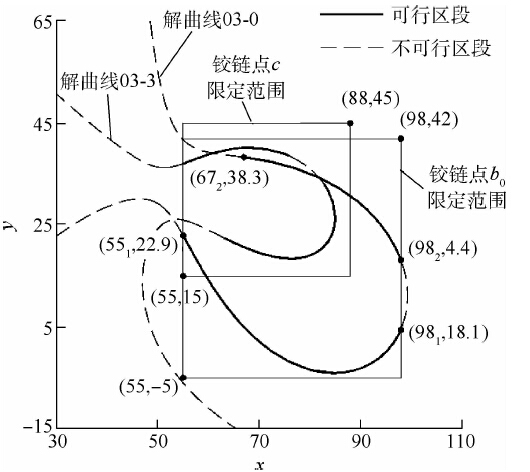 |
| 图 7 解曲线03-0和03-3Fig. 7 Solution curves of 03-3 and 03-3 |
根据表 2中的参数和固定铰链点a0坐标综合杆de,得到关于铰链点d和e坐标的解曲线13-1和13-3.再根据铰链点d和e限定范围求得可行区段,最终得到如图 8所示的解曲线.
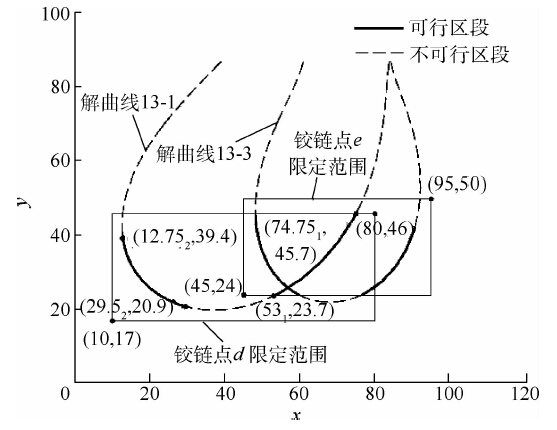 |
| 图 8 解曲线13-1和13-3Fig. 8 Solution curves of 13-1 and 13-3 |
为了建立机构解域,把图 7所示解曲线03-0的可行两区段依次向水平直线映射并相加作为横轴.区段1:xb0∈[551,981];区段2:xb0∈[672,982].同理,把图 8所示解曲线13-1的可行两区段依次向水平直线映射并相加作为纵轴.区段1:xd∈[531,74.751];区段2:xd∈[12.752,29.52].于是得如图 9a所示的机构解域.而后通过机构运动缺陷分析得如图 9b所示的无运动缺陷解域.最后添加约束条件,杆长比r≥0.25得到如图 9c所示的可行解域.
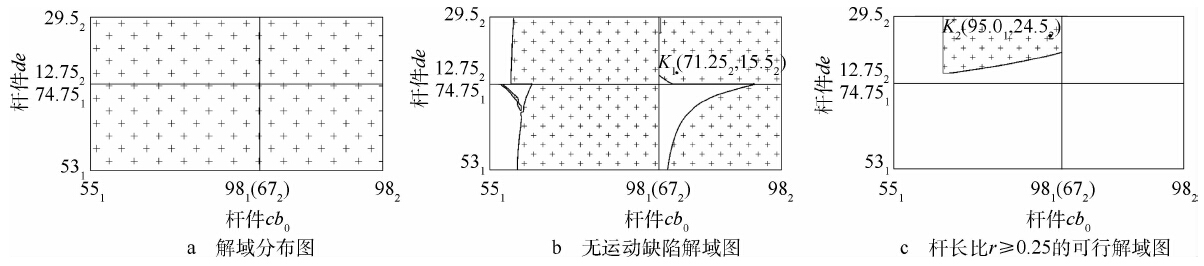 |
| 图 9 解域图Fig. 9 Solution regions |
在图 9c所示的可行域内任选一点都可得到满足设计要求的六杆机构.在图 9b上选择K1所示一点,得到如图 10a所示的无运动缺陷的六杆机构.在图 9c上选择K2所示一点,得到如图 10b所示的满足杆长比要求的机构.表 4列出了两个机构的坐标点和杆长比.
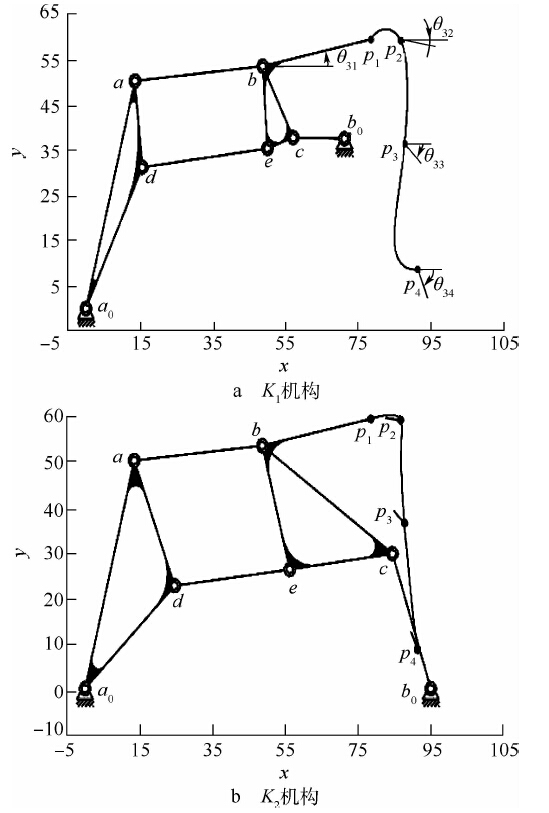 |
| 图 10 综合得到的机构Fig. 10 Synthesized linkage |
| 机构参数 | K1机构 | K2机构 |
| b0 | (71.25,37.66) | (95.0,0.0) |
| c | (57.11,37.88) | (84.47,29.82) |
| d | (15.50,31.28) | (24.5,22.79) |
| e | (50.00,35.47) | (56.18,26.40) |
| r | 0.0931 | 0.2989 |
1) 六杆机构四位置运动生成的解域综合方法为多杆机构运动生成的尺寸综合问题提供了新的理论、方法和有效的解决途径.
2) 利用解域综合法将可行机构解的信息在有限的范围内表示出来,避免了机构选择的盲目性.这对进一步研究可行机构解的性能以及可行机构解的优选具有一定的意义.
3) 所提出的机构缺陷判别方法是有效和实用的.
4) 综合示例所得到的结果表明所提出的理论和方法的正确性以及所开发软件的有效性.
| [1] | Kinzel E C,Schmiedeler J P,Pennock G R.Kinematic synthesis for finitely separated positions using geometric constraint programming[J].Journal of Mechanical Design,2006,128(5):1070-1079 |
| Click to display the text | |
| [2] | Yu H Y,Tang D,Wang Z X.Study on a new computer path synthesis method of a four-bar linkage [J].Mechanism and Machine Theory,2007,42(4):383-392 |
| Click to display the text | |
| [3] | Soh G S,McCarthy J M.The synthesis of six-bar linkages as constrained planar 3R chains[J].Mechanism and Machine Theory,2008,43(2):160-170 |
| Click to display the text | |
| [4] | Soh G S,Ying F,McCarthy J M.Dimensional synthesis of planar six-bar linkages by mechanically constrain a PRR serial chain [C]//ASME Design Engineering Technical Conferences,Proceedings of the ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.New York:American of Mechanical Engineers,2012:551-557 |
| [5] | McCarthy J M,Soh G S.Geometric design of linkages[M].2nd ed.New York:Springer,2011:141-143 |
| [6] | Soh G S,Ying F T.Dimensional synthesis of planar eight-bar linkages based on a parallel robot with a prismatic based joint[C]//ASME Design Engineering Technical Conferences,Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.New York:American Society of Mechanical Engineers,2013:V06AT07A051 |
| [7] | Han J Y,Qian W X.On the solution of region-based planar four-bar motion generation [J].Mechanism and Machine Theory,2009,44(2):457-465 |
| Click to display the text | |
| [8] | Yang T,Han J Y,Yin L R.A unified synthesis method based on solution regions for four finitely separated and mixed “Point-Order” positions[J].Mechanism and Machine Theory,2011,46(11):1719-1731 |
| Click to display the text | |
| [9] | Han J Y,Yang T.On the solution of region-based planar six-bar motion generation for four finitely separated positions[C]//ASME Design Engineering Technical Conferences,Proceedings of the ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.New York:American Society of Mechanical Engineers,2012:441-449 |
| Click to display the text | |
| [10] | Wang J,Ting K L,Xue C Y.Discriminant method for the mobility identification of single degree-of-freedom double-loop linkages[J].Mechanism and Machine Theory,2010,45(5):740-755 |
| Click to display the text | |
| [11] | Ting K L,Wang J,Xue C Y.Full rotatability and singularity of six-bar and geared five-bar linkages[J].Journal of Mechanisms and Robotics,2010,2(1):011011-1-9 |
| Click to display the text | |
| [12] | Watanabe K,Katoh H.Identification of motion domains of planar six-link mechanisms of the Stephenson-type [J].Mechanism and Machine Theory,2004,39(10):1081-1099 |
| Click to display the text | |
| [13] | Wang J,Ting K L.Mobility identification of a group of single degree-of-freedom eight-bar linkages[C]//ASME Design Engineering Technical Conferences,Proceedings of the ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.New York:American Society of Mechanical Engineers,2010:1739-1749 |
| [14] | Mirth J A,Chase T R.Circuit rectification for four precision position synthesis of Stephenson six-bar linkages[J].Journal of Mechanical Design,1995,117(4):644-646 |
| Click to display the text | |
| [15] | 韩建友.高等机构学[M].北京:机械工业出版社,2004:134-135 Han Jianyou.Advanced kinematics and dynamics of mechanisms[M].Beijing:China Machine Press,2004:134-135(in Chinese) |


