2. 中国核动力研究设计院, 成都 610200
2. Nuclear Power Institute of China, Chengdu 610200, China
T型管是石油、化工和核电管道系统中使用频率较高的结构,在主支管流体动量比很大的工况下,主管流体会侵入到支管,即湍流穿透现象。当湍流穿透区域与冷热流体混合区域重叠时,会引发流场内强烈的温度波动,管壁内部随之出现温度波动,使管道的热应力也产生波动[1],进而可能诱发高周热疲劳,使管道失效。
Kickhofel等[2]对带泄漏流的T型管内的湍流穿透现象进行了实验研究,得出湍流穿透速度波动的剧烈程度与主支管动量比之间的关系。Hirota等[3]对T型(三通)管内冷热流体混合过程进行了可视化实验,结果表明混合界面的垂直方向上会出现震荡以及旋涡叠加。卢涛等[4]利用大涡模拟(LES)方法对T型管道内冷热流体混合过程进行了数值计算,得出浮升力与混合过程波动情况的关系。Paffumi等[5]对材料为316L不锈钢的管道进行疲劳试验,研究了温差、轴向力以及壁厚对热疲劳的影响。Lee等[6]运用大涡模拟获得了近壁面流体的温度波动,研究发现冷热流体温差和由湍流混合引起的强化对流换热是T型管道疲劳失效的主要因素。张越[7]使用瞬态界面耦合方法对管道进行应力分析,计算了管道疲劳寿命。综上所述,目前对于T型管内流动与热现象的研究多集中于热分层。此外,关于流固耦合的研究多为稳态耦合或瞬态面耦合,体节点的数据需要在耦合计算过程重新插值,而流场分析软件一般使用有限体积法,固体分析软件一般使用有限单元法,重新插值计算得到的数据存在误差。
本文使用Fluent软件对T型管湍流穿透区域的流体速度与温度场进行分析,得出管内各物理量的时空演变规律;使用用户自定义函数(UDF)、批处理文件(Journal)以及CFD-Post软件中的宏计算器(Macrocalculator)进行数据提取,通过ANSYS Workbench平台动态加载到管道内部,确保每一时间步内网格节点温度完全耦合,得到固体应力波动信息并对危险点的疲劳寿命进行评估。
1 计算模型 1.1 数学模型T型管内湍流穿透现象伴随着流场温度与速度的剧烈波动,因此需要进行瞬态分析。与使用时均方法的k-ε模型相比,大涡模拟方法可以较好地捕捉管内流体温度与速度的瞬时波动细节[8-11],因此本文使用大涡模拟方法进行流场数值计算。对于不同的大涡模拟湍流模型,其本质区别在于亚格子(SGS)模型不同,亦即如何描述亚格子雷诺应力。
亚格子雷诺应力可以定义为
| $ {\tau _{ij}} = \rho {\kern 1pt} {\kern 1pt} \overline {{u_i}{u_j}} - \rho {\bar u_i}{\bar u_j} $ | (1) |
SGS模型通常使用涡-黏模型计算,即
| $ {\tau _{ij}} - \frac{{{\tau _{kk}}{\delta _{ij}}}}{\varepsilon } = - 2{\mu _{\rm{t}}}{\bar s_{ij}} $ | (2) |
式中τ为亚格子应力,μt为SGS湍流黏度,s表示已经求解的应变率张量,δij为克罗内克符号。
本文采用Smagorinsky-lily亚格子湍流黏度
| $ {\mu _{\rm{t}}} = \rho L_{\rm{s}}^2|\bar s{|^2} $ | (3) |
其中Ls表示亚格子尺度的混合长度,即
| $ {L_{\rm{s}}} = {\rm{min}}(kd,{C_{\rm{S}}}{V^{1/3}}) $ | (4) |
式中,k为冯卡门常数,k=0.41;d为到最近的壁面的距离;CS为Smagorinsky常数,取值0.1;V为计算单元体积。
T型管冷热流体掺混过程中,重力与浮升力共同发生作用。在大涡模拟模型的动量方程中,针对浮升力项的求解需要对流体进行变物性设置。根据水的物性表[7]对其密度随温度的变化进行拟合,得到三阶多项式
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho = 750.596 + 2.145{\kern 1pt} {\kern 1pt} {\kern 1pt} 03 \times T - 0.005{\kern 1pt} {\kern 1pt} {\kern 1pt} 12 \times {T^2} + \\ 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 002{\kern 1pt} {\kern 1pt} {\kern 1pt} 312 \times {T^3} \end{array} $ | (5) |
式中ρ为流体密度,kg/m3;T为流体温度,K。
使用有限元方法对耦合热应力与应变进行求解,将流场计算的温度场作为载荷对固体域进行计算,具体理论模型为[12]
| $ \mathit{\boldsymbol{\sigma }} = \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{\varepsilon }} - {\mathit{\boldsymbol{\varepsilon }}_0}) $ | (6) |
式中,D为弹性矩阵,ε0为温度变化引发的变形量
| $ {\mathit{\boldsymbol{\varepsilon }}_0} = \alpha \Delta T{\left[ {\begin{array}{*{20}{l}} 1&1&1&0&0&0 \end{array}} \right]^{\rm{T}}} $ | (7) |
式中,α为材料的线膨胀系数,ΔT为温度变化。
ε可由式(8)求得
| $ \mathit{\boldsymbol{\varepsilon }} = \mathit{\boldsymbol{B}}{\delta _{\rm{e}}} $ | (8) |
其中B为应变矩阵,节点位移δe可由式(9)求出
| $ \mathit{\boldsymbol{K}}{\delta _{\rm{e}}} = {\mathit{\boldsymbol{Q}}_{\rm{T}}} $ | (9) |
式中,K为刚度矩阵, QT为受到的热载荷。
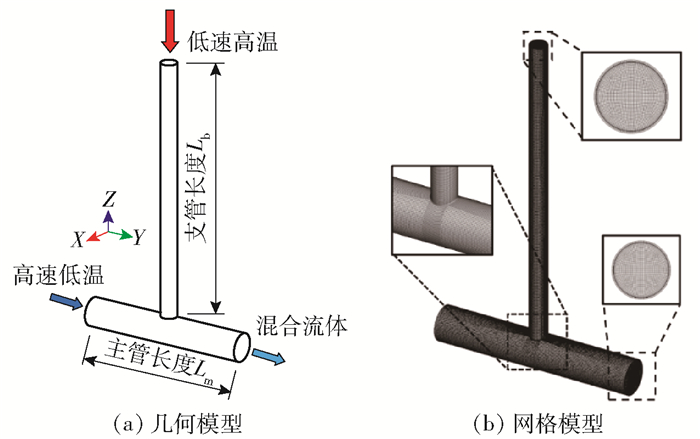
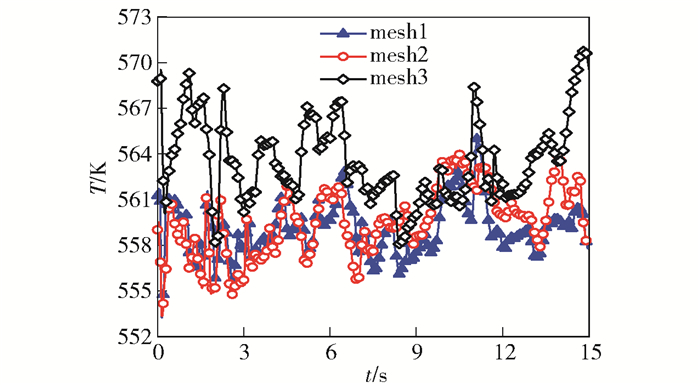
1.2 物理模型主管长530 mm,内径120 mm,壁厚3.5 mm; 支管长1 100 mm,内径60 mm,壁厚2.5 mm。对流体域与固体域同时划分全结构化网格。几何模型与网格模型如图 1所示,网格数量为962 339,第一层网格高度为0.01 mm,边界层网格增长率为1.1,层数为15,y+值为4。网格无关性验证如图 2所示,分别对3种不同网格数量的模型(mesh1 1 825 205;mesh2 962 339;mesh3 405 416)进行计算,得到管内H=2.5截面,90°位置点温度随时间的变化曲线。从图 2可以看出,mesh1、mesh2计算结果相差较小,为兼顾计算精度与计算效率,下文采用mesh2作为流固耦合计算网格。
|
图 1 计算模型 Fig.1 Model of the simulation |
|
图 2 网格无关性验证 Fig.2 Results of the grid independence test |
为便于定量探究管内流体温度与速度随时间的变化情况,分别定义速度及温度的统计量。
定义轴向时均速度Vz, mean
| $ {V_{z,{\rm{ mean }}}} = \frac{1}{N}\sum\limits_{i = 1}^N {{V_{z,i}}} $ | (10) |
定义轴向均方根速度Vz, rms
| $ {V_{z,{\rm{rms}}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {({V_{z,i}} - {V_{z, {\rm{mean}} }})} } $ | (11) |
绝对速度Vi为
| $ {V_i} = \sqrt {{{({V_{x,i}})}^2} + {{({V_{y,i}})}^2} + {{({V_{z,i}})}^2}} $ | (12) |
式中,Vx, i、Vy, i、Vz, i分别为i时刻x、y、z方向的速度大小,对于支管,z方向速度即为轴向速度,单位为m/s。
时均绝对速度Vmean
| $ {I_{{\rm{ mean }}}} = \frac{1}{N}\sum\limits_{i = 1}^N {{V_i}} $ | (13) |
均方根绝对速度Vrms
| $ {V_{{\rm{rms}}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {({V_i} - {V_{{\rm{mean}}}})} } $ | (14) |
无量纲温度Ti*
| $ T_i^* = \frac{{{T_i} - {T_{{\rm{ cold }}}}}}{{{T_{{\rm{ hot }}}} - {T_{{\rm{ cold }}}}}} $ | (15) |
无量纲时均温度Tmean*
| $ T_{{\rm{mean}}}^* = \frac{1}{N}\sum\limits_{i = 1}^N {T_i^*} $ | (16) |
无量纲均方根温度Trms*
| $ T_{{\rm{rms}}}^* = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {(T_i^* - T_{{\rm{mean}}}^*)} } $ | (17) |
定义支管轴向无量纲高度为
| $ H = \frac{{z - ({D_{\rm{m}}}/2 + t)}}{{{D_{\rm{b}}}}} $ | (18) |
式中,N为采样时间点总数,i为采样时刻序号,Tcold为主管入口温度,Thot为支管入口温度,z为轴向高度坐标,Dm为主管直径,t为主管厚度,Db为支管直径。
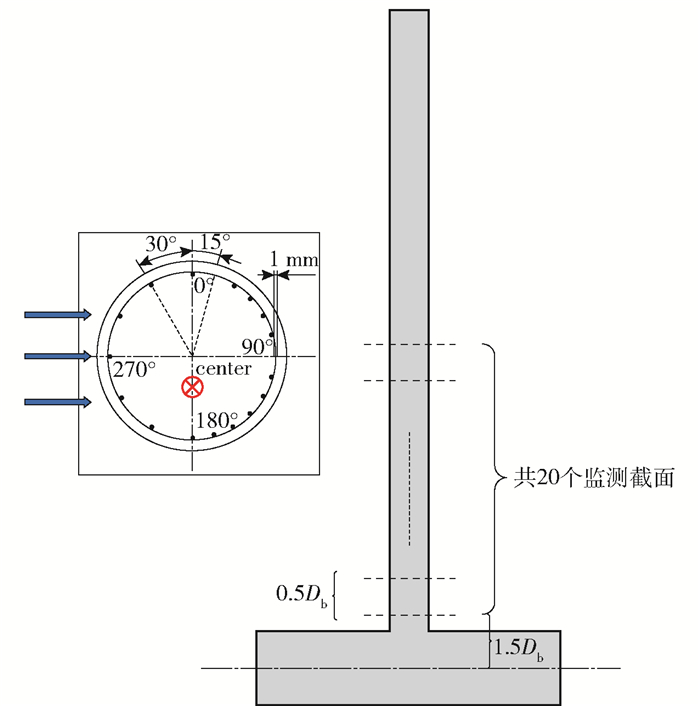
2 参数设置 2.1 流场计算流场计算的具体边界条件见表 1。计算过程中,按主管入口边界条件进行初始化,设置操作压力为15.5 MPa。首先使用k-ε模型进行稳态计算,当流动达到稳定时开启瞬态LES模型,使用couple耦合求解器与二阶迎风格式求解。瞬态求解总时间为15 s,时间步长为0.005 s,数据监测频率为200 Hz。沿支管轴向方向共设置20个监测截面,每个截面设置多个近壁面监测点,其中0°到180°的区域(正半区)正对来流方向,波动较剧烈,因此该区域沿周向每隔15°设置一个监测点,背对来流方向的位置(负半区)每隔30°设置一个监测点,监测近壁面1 mm处温度与速度波动信息。具体设置情况见图 3。
| 下载CSV 表 1 流场计算边界条件 Table 1 Boundary conditions in the CFD simulation |
|
图 3 监测截面与监测点设置 Fig.3 Monitor surfaces and points |
瞬态流固耦合计算分为单向和双向,在实际运行过程中,管道的变形相对较小,对流场的影响可以忽略不计,因此选择单向耦合方法进行计算。将流场计算结果如管道内壁面压力、固体域温度等作为载荷动态加载到固体域,加载时间步长为0.025 s,耦合计算时间共5 s,导入5~10 s内的流场数据。
根据实际情况选择管道材料为316L不锈钢,具体边界条件如表 2所示。
| 下载CSV 表 2 流固耦合计算边界条件 Table 2 Boundary conditions of the CFD-FEM simulation |
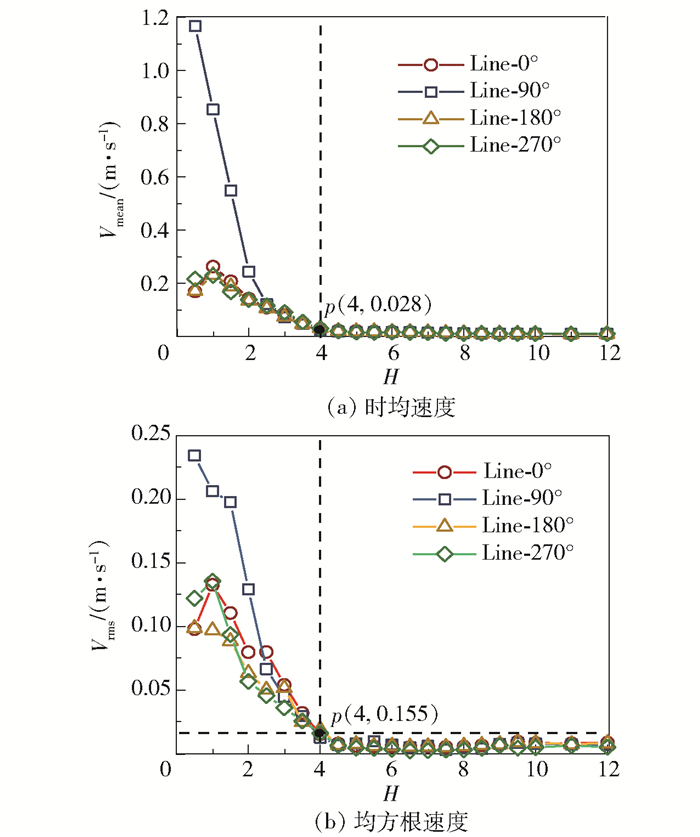
在湍流穿透发生的区域,流场的流动情况十分复杂,在各个方向上均存在强烈的速度波动,本文主要探究速度波动的强度沿管道轴向以及周向的分布,因此对绝对速度V的时均值及均方根值进行分析。图 4为Vmean与Vrms沿轴向的分布情况。
|
p为曲线降至稳定点位置。 图 4 速度的轴向分布 Fig.4 Axial distributions of Vmean and Vrms |
分析图 4(a),当H < 2时,对比同一截面不同位置的时均速度,90°处的值远高于其他位置的值,这是由于主管流体在流经交汇处时,由于流动截面积突增,流动方向压力变大,致使流动速度逐渐减小至0,由负半区侵入支管;当H>2.5时,90°位置的时均速度迅速下降至与其他位置几乎相同,原因是主管流体侵入支管后,遇到速度相反的支管流体,向上的动量被迅速抵消;从H=4位置开始,曲线斜率几乎为0,说明此区域内占主导地位的是支管的低速流体。
图 4(b)中曲线呈现的规律与图 4(a)相似,90°位置的波动在H < 2时远高于同截面的其他位置,但在H=2.5附近,0°曲线对应值略高于90°,说明速度波动峰值的周向位置并不完全固定,由于流体的湍流特性,偶尔会在其他位置出现;在H=4处,曲线值接近0,说明在当前工况下,湍流穿透的深度为H=4;注意到在10 < H < 12区域,曲线有小幅的上升,说明支管下游的速度波动会对上游产生轻微扰动,由于该扰动相对下游可以忽略不计,且该区域处于热稳定区,故本文不对其作进一步探究。
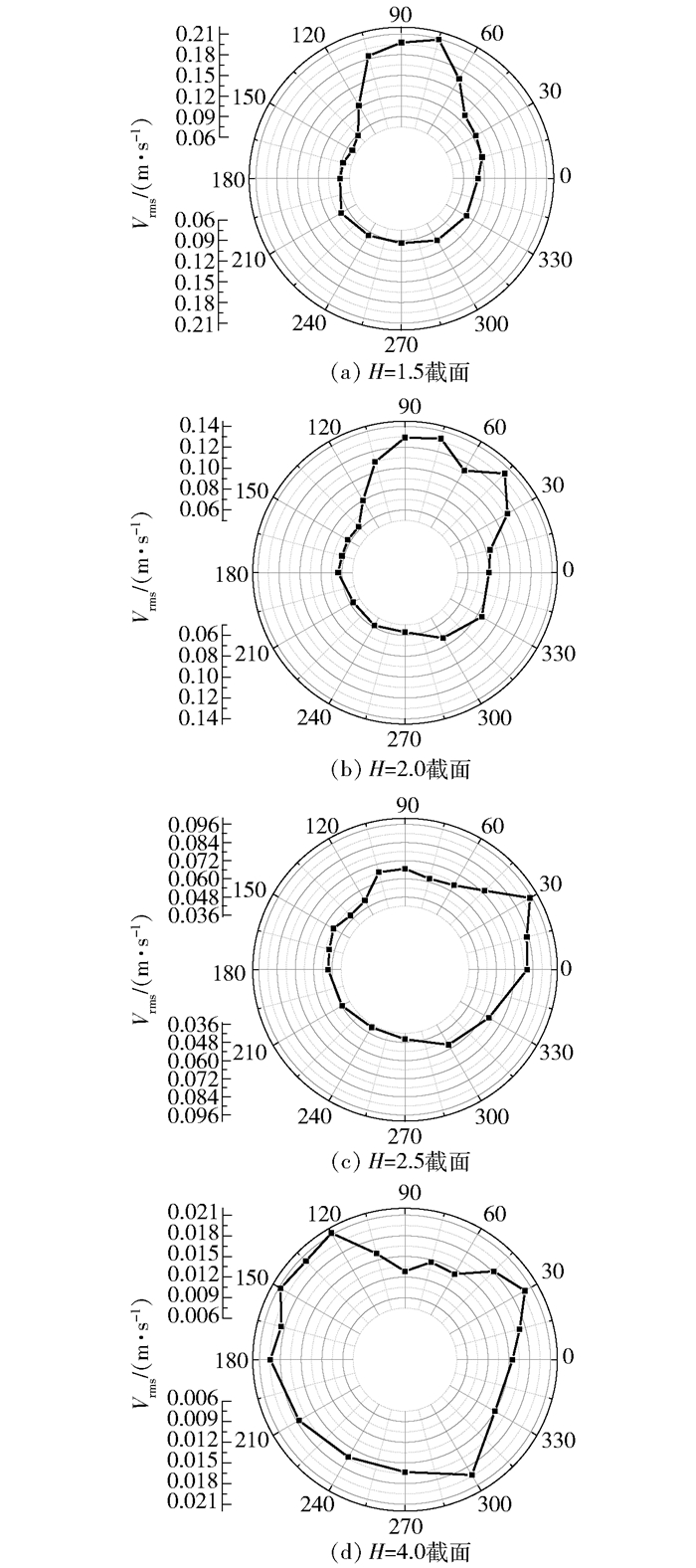
进一步就速度波动峰值的周向位置不固定的现象进行分析。图 5为不同高度截面上Vrms的周向分布情况。
|
图 5 均方根绝对速度周向分布情况 Fig.5 Circumferential distribution of Vrms |
对比图 5中的4幅图,可以发现随着截面轴向高度的增加,均方根速度峰值出现的位置在不断变化。当H分别为1.5、2.0、2.5时,峰值出现的位置为75°、75°、30°,其中前两个截面峰值位置相同,但波动幅度较大区域存在明显的偏转;当H=4.0时,曲线的周向分布相对均匀,峰值与谷值之间相差很小,可以认为在该位置速度波动已趋于平缓,与图 4分析结果一致;此外,还注意到H=1.5~2.5截面曲线峰值的偏转方向为顺时针,这与流体进入支管后受到的初始扰动有关。
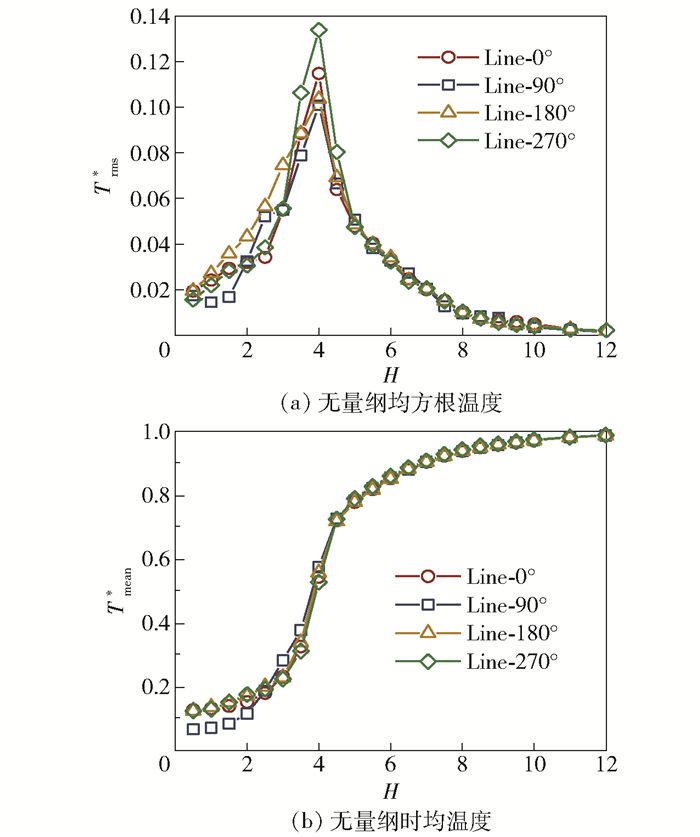
3.1.2 温度场分析图 6为无量纲温度统计量的轴向分布。由图 6(a)可以看出,在湍流穿透工况下,波动管内近壁面流场温度的波动强度随轴向高度的增加先增大后减小,在H=4位置达到峰值,且在该高度附近位置波动强度变化幅度很大,原因是该截面以下为速度湍流穿透区域,主管低温流体在该区域占主导地位,支管流体还未流到该区域就被冷却;当主管流体向上侵入至H=4高度时,其动量被支管流体完全抵消,此位置温度升高的速度急剧增大;当H>4时,流体温度达到稳定,处于热稳定区,波动强度减弱,最终降低为0。
|
图 6 无量纲温度轴向分布 Fig.6 Axial distributions of Trms* and Tmean* |
由图 6(b)可以看出,流体平均温度随轴向高度增加而升高,曲线斜率先增大后减小,当H=4时为最大值,该位置对应流体温度波动最强烈的区域。
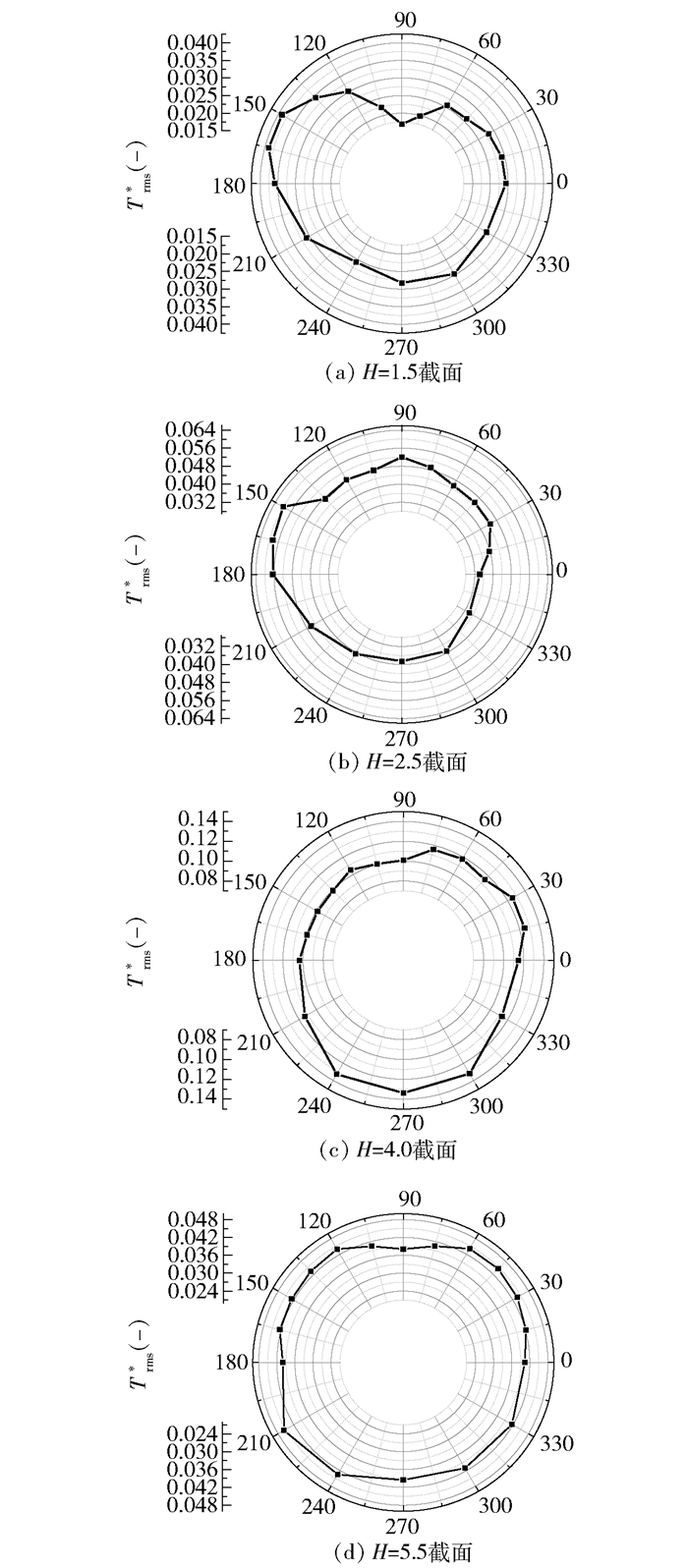
图 7为不同截面上无量纲均方根温度的周向分布情况。可以发现随着轴向高度的增加,不同截面的均方根温度峰值在正负半区交替出现,当H为1.5、2.5时,峰值出现在正半区,当H=4.0时,峰值出现在负半区,此截面处温度波动达到最大;当H=5.5时,均方根温度的周向分布趋于均匀,峰值与谷值之间相差很小,说明此区域已处于热稳定区。
|
图 7 无量纲均方根温度周向分布 Fig.7 Circumferential distribution of Trms* |
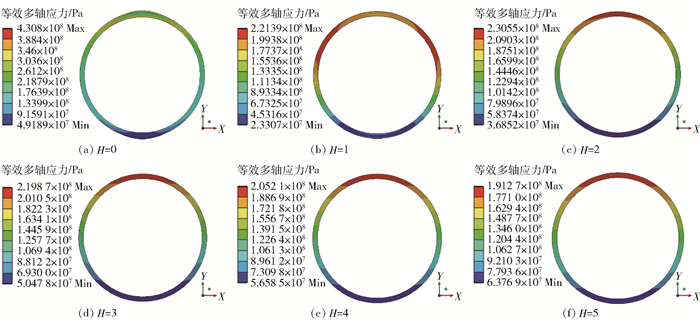
首先对耦合计算的应力结果进行分析。图 8为T型管不同轴向高度截面的应力云图,可以看出,在H=0截面,最大应力出现的区域分别在管道0°及90°位置的内壁面处,这是由于该区域为相贯区,存在应力集中效应;当H>2时,应力最大位置出现在270°位置,原因是支管受到热载荷产生热应力与热变形,从而沿管道轴向方向膨胀,由于主支管入口皆为固定约束,该膨胀导致主管出口产生Z方向的变形;对比不同截面高度的应力分布,从H=0截面开始,在270°位置应力先增大后减小,这是由冷热流体在该区域掺混产生的热应力引起。
|
图 8 10 s时不同高度截面的等效多轴应力分布 Fig.8 Plots of the von-Mises stress distribution with different axial heights at 10 s |
对危险点处的应力波动信息进行处理,使用疲劳分析理论进行评估。疲劳问题分为高周疲劳与低周疲劳,后者主要针对单次应力循环较大且循环次数较低的情况,本文研究的湍流穿透工况管道单次循环应力较小,实际循环次数远高于105,因此属于高周疲劳,需要分析名义应力,并使用S-N曲线进行疲劳评估。
对于等效多轴应力的波动信息,使用雨流计数法[13]统计其全循环次数,得到雨流矩阵N, 再依据Goodman曲线进行等效,得到等效对称循环应力矩阵NG。
Goodman理论的具体公式为
| $ \frac{{{S_{\rm{a}}}}}{{{S_{{\rm{a( - 1)}}}}}} + \frac{{{S_{\rm{m}}}}}{{{S_{\rm{u}}}}} = 1.0 $ | (19) |
式中,Sa(-1)为修正后的等效对称应力,Sa为应力幅,Sm为平均应力,Su为材料的极限强度。本文使用的316L不锈钢的强度极限取520 MPa。
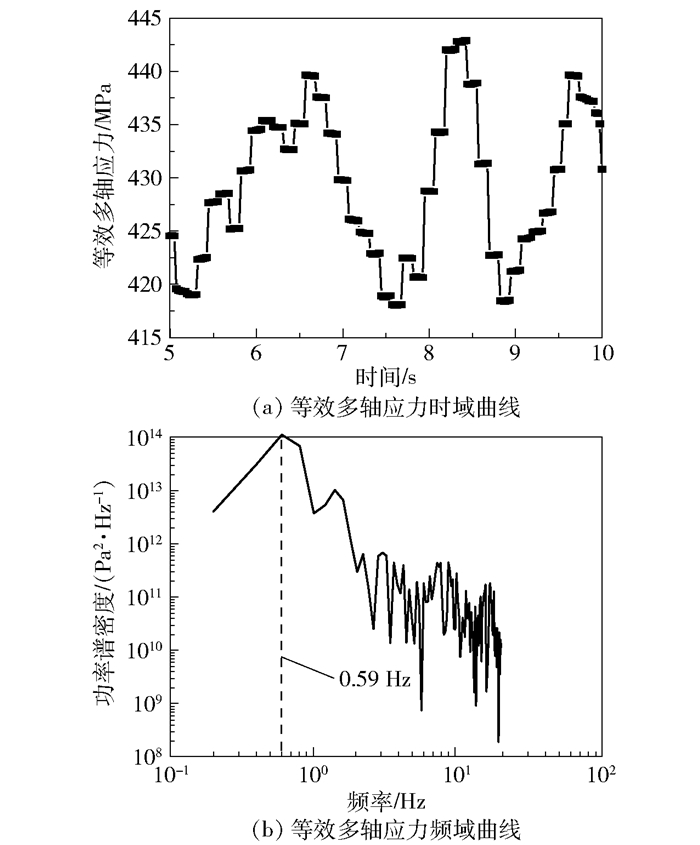
根据应力分析,选定H=0截面的最大应力点作为分析对象,该点的等效多轴应力波动情况如图 9所示。
|
图 9 应力波动情况 Fig.9 Stress fluctuation information |
对应力波动信息进行频域分析,由图 9(b)可看出,功率谱密度曲线最大值对应的频率为0.59 Hz,其周期为1.69 s。由于在耦合计算的前5 s及其后续的计算时间内流场与固体场各物理量的波动状态较为稳定,且5 s的时间包含应力波动的主周期,因此以5 s内的数据作为代表,为便于雨流计数法分析,将其延拓至25 s。
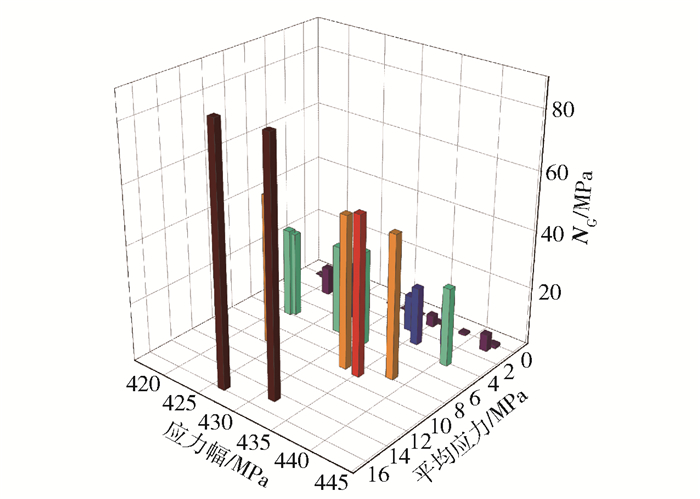
图 10为雨流计数法得到的应力雨流矩阵,图 11为对雨流矩阵进行修正处理后得到的Goodman修正应力矩阵。

|
图 10 雨流矩阵N Fig.10 Rainflow matrix N |
|
图 11 Goodman修正应力矩阵NG Fig.11 Goodman stress matrix NG |
除平均应力与应力幅外,材料的表面粗糙度、缺口、介质的腐蚀性均会加剧疲劳裂纹的产生,对于实际管路,高速运行的流体还会产生振动,因此在对管路进行疲劳评估时,所考虑的循环载荷以及对应的寿命曲线需要作更保守的处理。本文采用文献[7]的处理方法,定义一个安全系数K,将等效对称应力与之相乘,得到最终等效循环应力Sa(-1)*。本文的K值取1.1。将ASME奥氏体标准S-N疲劳寿命曲线外推至Sa(-1)*在100 MPa以下,外推公式为
| $ {\rm{lg}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {N_{{\rm{ fitting }}}} = - 0.846{\kern 1pt} {\kern 1pt} {\kern 1pt} 7 \times S_{{\rm{a( - 1)}}}^* + 90.15 $ | (20) |
式中Nfitting为Goodman修正应力对应的循环次数。
根据Miner疲劳累计损伤准则得到累计疲劳损伤Df为
| $ {D_{\rm{f}}} = \sum {\frac{{{N_{ij}}}}{{{N_{ij,{\rm{ fitting }}}}}}} $ | (21) |
由式(21)得Df=1.657 7×10-8,疲劳寿命L=1/Df=6.032 4×107个周期,每个周期25 s,最终得到该位置的寿命为47.82年。
4 结论(1) 使用大涡模拟湍流模型预测了T型管交汇处流体的流动与传热情况,发现在支管轴向无量纲高度H=4截面处温度波动强度最大。
(2) 构建了热-流-固耦合方法,获得了管道热应力的空间分布情况与瞬态波动信息,确定了管道疲劳失效的危险点为轴向无量纲高度H=0截面上的应力集中位置。
(3) 对危险点的热应力波动信息进行处理,通过疲劳分析理论得到了该结构的疲劳寿命为47.82年。
| [1] |
MESHII T, SHIBATA K, WATANABE K. Simplified method to evaluate upper limit stress intensity factor range of an inner-surface circumferential crack under steady state thermal striping[J]. Nuclear Engineering and Design, 2006, 236: 1081-1085. DOI:10.1016/j.nucengdes.2005.10.013 |
| [2] |
KICKHOFEL J, VALORI V, PRASSER H M. Turbulent penetration in T-junction branch lines with leakage flow[J]. Nuclear Engineering and Design, 2014, 276: 43-53. DOI:10.1016/j.nucengdes.2014.05.002 |
| [3] |
HIROTA M, MOHRI E, ASANO H, et al. Experimental study on turbulent mixing process in cross-flow type T-junction[J]. International Journal of Heat and Fluid Flow, 2010, 31: 776-784. DOI:10.1016/j.ijheatfluidflow.2010.04.006 |
| [4] |
卢涛, 朱兴国. 浮升力对T型管道内冷热流体混合过程热波动的影响[J]. 热科学与技术, 2011, 10(4): 305-311. LU T, ZHU X G. Influence of buoyancy on thermal fluctuation of fluid mixing in T-junction[J]. Journal of Thermal Science and Technology, 2011, 10(4): 305-311. (in Chinese) DOI:10.3969/j.issn.1671-8097.2011.04.006 |
| [5] |
PAFFUMI E, NILSSON K F, TAYLOR N G. Simulation of thermal fatigue damage in a 316L model pipe component[J]. International Journal of Pressure Vessels and Piping, 2008, 85: 798-813. DOI:10.1016/j.ijpvp.2008.06.002 |
| [6] |
LEE J I, HU L W, SAHA P, et al. Numerical analysis of thermal striping induced high cycle thermal fatigue in a mixing tee[J]. Nuclear Engineering and Design, 2009, 239: 833-839. DOI:10.1016/j.nucengdes.2008.06.014 |
| [7] |
张越.压水堆波动管流动与传热及热-力耦合结构应力、变形与疲劳研究[D].北京: 北京化工大学, 2017. ZHANG Y. The coupled thermo-hydro-mechanical analysis and thermal fatigue assessment for the pressurizer surge line[D]. Beijing: Beijing University of Chemical Technology, 2017. (in Chinese) |
| [8] |
HOWARD R J A, SERRE E. Large-eddy simulation in a mixing tee junction:high-order turbulent statistics analysis[J]. International Journal of Heat and Fluid Flow, 2015, 51: 65-77. DOI:10.1016/j.ijheatfluidflow.2014.11.009 |
| [9] |
MING T Z, ZHAO J Y. Large-eddy simulation of thermal fatigue in a mixing tee[J]. International Journal of Heat and Fluid Flow, 2012, 37: 93-108. DOI:10.1016/j.ijheatfluidflow.2012.06.002 |
| [10] |
SELVAM P K, KULENOVIC R, LAURIEN E. Large eddy simulation on thermal mixing of fluids in a T-junction with conjugate heat transfer[J]. Nuclear Engineering and Design, 2015, 284: 238-246. DOI:10.1016/j.nucengdes.2014.12.025 |
| [11] |
TIMPERI A. Conjugate heat transfer LES of thermal mixing in a T-junction[J]. Nuclear Engineering and Design, 2014, 273: 483-496. DOI:10.1016/j.nucengdes.2014.02.031 |
| [12] |
ZHANG Y, LU T. Study of the quantitative assessment method for high-cycle thermal fatigue of a T-pipe under turbulent fluid mixing based on the coupled CFD-FEM method and the rainflow counting method[J]. Nuclear Engineering and Design, 2016, 309: 175-196. DOI:10.1016/j.nucengdes.2016.09.021 |
| [13] |
MCINNES C H, MEEHAN P A. Equivalence of four-point and three-point rainflow cycle counting algorithms[J]. International Journal of Fatigue, 2008, 30: 547-559. DOI:10.1016/j.ijfatigue.2007.03.006 |








