2. 无锡新宏泰电器科技股份有限公司, 无锡 214174
2. Wuxi XinHongTai Electrical Appliance Technology Co., Ltd., Wuxi 214174, China
聚酯通常是指二元醇与二元酸经过缩聚得到的高分子化合物,此类聚合物作为一种性能优异、用途广泛的工程塑料[1-2],主要包括聚对苯二甲酸乙二酯(PET)[3]、聚对苯二甲酸丁二酯(PBT)[4]、聚芳酯(PAR)[5]等。由于二元醇和二元酸的种类较多,醇酸组合方式不同,制得的聚酯就不同,所以聚酯的种类繁多。另外由于聚酯的制备成本低廉,其应用领域较为宽泛,包括包装、汽车、建筑、医疗等领域[6-8]。然而随着时代的发展,聚酯本身的性能已无法满足社会发展的多种需求,于是人们根据需求对聚酯进行了许多改性,如低熔点聚酯[9]、不饱和聚酯、耐热性聚酯以及阻燃性聚酯等。
Jing等[10]通过对苯二甲酸、乙二醇、二甘醇(DEG)和3-羟基苯基磷酰丙酸(HPPPA)的酯化缩聚反应,合成了具有低熔融温度的含磷聚对苯二甲酸乙二酯-共-对苯二甲酸二乙酯(PEDT)。PEDT的最低熔融温度可降低至118.0 ℃,添加HPPPA可以提高聚酯的热氧化稳定性,增大其极限氧指数,使PEDT具有良好的阻燃性能。不饱和聚酯树脂是得到广泛使用的一种热固性树脂,能够作为树脂基体,通过与玻璃纤维、填料等混合制备模塑料,也能够通过改性制备成各种模塑料的添加剂。许小强等[11]利用对苯二甲酸、乙二醇、1,4-丁二醇、顺丁烯二酸酐等合成了可作为模塑料流平添加剂的结晶性不饱和聚酯,结果表明:通过调整1,4-丁二醇的用量可以改变合成树脂的熔点及结晶性能。赵萍[12]利用对苯二甲酸、间苯二甲酸、乙二醇和二甘醇反应制备了低熔点的结晶性共聚酯热熔胶,并运用Avrami动力学方程及其修正模型,探讨了共聚物等温结晶和非等温结晶的过程,结果表明:DEG的增加阻碍了等温熔融结晶的进行;Khann a-Taylor法和Mo法两种方法都比较适合用于共聚酯热熔胶的非等温结晶动力学分析。王赛博[13]采用共聚法制备了低熔点聚酯,并分别用Jeziorny法和Mo法对聚酯体系进行了非等温结晶动力学分析,结果表明:共聚酯存在次级结晶且不可忽略,Mo法更适合处理低熔点共聚酯的非等温结晶问题。
目前已有许多与聚酯改性制备相关的研究工作,但对于不饱和结晶性聚酯的结晶行为并未有系统的讨论与研究。本文主要利用Avrami方程及其修正方程、Ozawa法和Mo法对不饱和结晶性聚酯进行等温和非等温的结晶行为研究,分析得到不饱和结晶性聚酯合适的结晶条件和结晶行为分析方法,同时对不饱和结晶性聚酯的结晶形貌进行观察,结合非等温结晶行为分析结晶性聚酯的结晶形貌以及不同结晶条件对形貌的影响。
1 实验部分 1.1 原料及设备1,6-己二醇、丁基锡酸,分析纯,国药集团化学试剂有限公司;乙二醇、对苯二甲酸,分析纯,上海凌峰化学试剂有限公司;顺丁烯二酸酐,分析纯,萨恩化学技术(上海)有限公司。
DSC 200 F3 Maim@差示扫描量热分析仪(DSC),德国Netzsch公司;59X C-PC偏光显微镜,上海光学仪器一厂;GPC Waters1515凝胶渗透色谱仪-THF(GPC),美国Waters公司;Nicolet 6700傅里叶变换红外光谱(F T-IR)仪,美国热电公司。
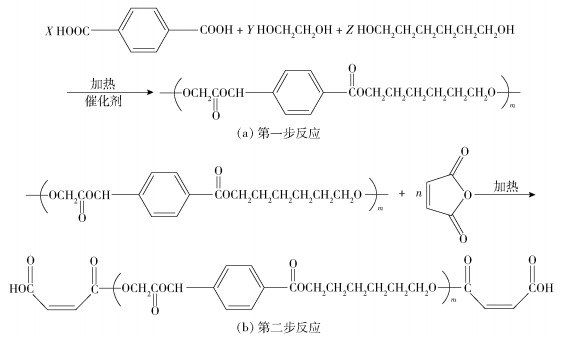
1.2 不饱和结晶性聚酯的制备不饱和结晶性聚酯采用“两步法”合成[14]:(1)将原料按照物质的量比为1,6-己二醇:乙二醇=2.5 :1,对苯二甲酸:顺丁烯二酸酐=4 :1的配比投入反应釜中并加入有机锡催化剂,待物料全部熔化后升温至180 ℃,反应3 h后梯度升温(10 ℃/min)至220 ℃,保温1 h后,第一步反应结束,反应原理式如图 1(a)所示;(2)在反应釜温度降低到160 ℃后加入顺丁烯二酸酐,升温至180 ℃反应3 h后测酸值,反应原理式如图 1(b)所示。采用氢氧化钾的甲醇溶液滴定检测产物的酸值[15],当酸值小于30时,则停止反应,将产物倒出,冷却后得到不饱和结晶性聚酯。
|
图 1 不饱和结晶性聚酯的反应原理图 Fig.1 Synthesis of the unsaturated crystalline polyester |
采用傅里叶变换红外光谱仪对样品进行检测,测试范围4 000~350 cm-1,最高分辨率0.09 cm-1。由于合成的聚酯为固体,故而采用压片法将待测样品和纯溴化钾研磨粉碎并混合均匀后压制成薄片,置于F T-IR仪中后开始扫描并进行数据采集。
1.4 GPC表征由于本文合成的结晶性聚酯在四氢呋喃中有较好的溶解性,故选择流动相溶剂为四氢呋喃进行测试。首先将待测试的结晶性聚酯在60 ℃真空烘箱中放置2 h进行干燥,之后称取小于2 mg的样品在35 ℃下进行测试,得到结晶性聚酯的相对分子量及分子量分布。
1.5 DSC熔点测试取不饱和结晶性聚酯5~10 mg放置于DSC坩埚内,在氮气气氛保护下分别以10 ℃/min、20 ℃/min、30 ℃/min的升温速率从室温升至150 ℃,测定结晶性聚酯的熔融曲线。
1.6 等温结晶性能测试取不饱和结晶性聚酯5~10 mg,放置于DSC坩埚内,在氮气气氛保护下以30 ℃/min的升温速率快速升温至150 ℃,保温5 min确保称取的样品完全熔融。再以30 ℃/min的速率快速降温至结晶温度50 ℃,并维持在所设定的结晶温度,使不饱和聚酯在设定的温度下进行充分的结晶,待20 min结晶基本完成后,再将样品的温度以30 ℃/min的升温速率快速升温至150 ℃,保温5 min确保样品完全熔融,设定结晶温度分别为50、55、60、65、70 ℃,测定低熔点聚酯的等温结晶曲线以及对应结晶温度下的熔融温度Tm。
1.7 非等温结晶性能测试取不饱和结晶性聚酯5~10 mg,放置于DSC坩埚内,在氮气气氛保护下以30 ℃/min的升温速率快速升温至150 ℃,保温5 min确保样品完全熔融。分别以2.5、5、10、15 ℃/min以及20 ℃/min的降温速率降温至0 ℃,测定其结晶温度Tc以及对应的冷却结晶曲线。
1.8 偏光显微镜观察结晶性聚酯的结晶形貌首先将标准片在400倍倍率下与目镜刻度对比,计算目镜刻度在此倍率下的尺寸,然后将恒温台升温至150 ℃,待温度稳定后,放上载玻片和样品,压制成熔融的透明薄片,放置于恒温炉内进行等温结晶,结晶15 min后取出,放置于偏光显微镜上,在400倍倍率下观察结晶性聚酯的结晶形貌。分别设定恒温炉温度为50、55、60 ℃,观察对应温度结晶后的形貌,并利用目镜刻度尺寸估测出球晶的大小。
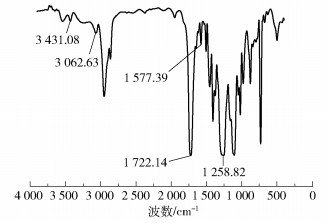
2 结果与讨论 2.1 不饱和结晶性聚酯的FT-IR及GPC分析结果图 2是合成的不饱和结晶性聚酯的F T-IR谱图,其中3 431.08 cm-1处为—COOH缔合的伸缩振动峰,3 062.63 cm-1处为苯环中C—H的伸缩振动峰,1 722.14 cm-1处为酯键中—C=O的伸缩振动峰,1 577.39 cm-1处为苯环中C=C的振动吸收峰,1 258.82 cm-1处为链段羧基中C—O的伸缩振动峰。这些对应的红外特征峰与设计的分子的特征峰吻合。
|
图 2 不饱和结晶性聚酯的F T-IR谱图 Fig.2 F T-IR spectrum of the unsaturated crystalline polyester |
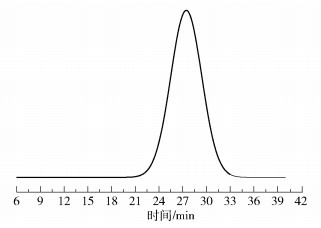
由表 1和图 3可知,合成的聚酯峰值分子量为13 772,分散系数为1.46,说明“两步法”合成的不饱和结晶性聚酯分子量及其分布都得到了较好的控制。
| 下载CSV 表 1 不饱和结晶性聚酯的分子量信息 Table 1 Molecular weight details of the unsaturated crystalline polyester |
|
图 3 不饱和结晶性聚酯的GPC Fig.3 GPC trace of the unsaturated crystalline polyester |
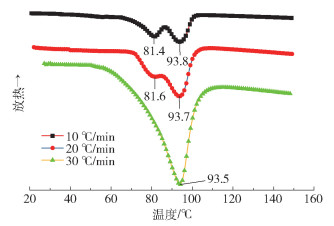
不饱和结晶性聚酯在不同升温速率下的熔融曲线如图 4所示,可以看出,不饱和聚酯的熔融峰为两重峰,且随着升温速率增大,两重峰逐渐靠近,当升温速率增加至30 ℃/min时,只在93.5 ℃出现一个熔融峰。这是因为不饱和结晶性聚酯由结晶完善部分和结晶不完善部分组成,在升温速率较小时,结晶不完善的聚酯开始熔化出现熔融峰,随着温度升高结晶不完善部分的熔化几乎完成,结晶较完善的聚酯逐渐开始熔化而再次出现一个熔融峰,所以升温速率较小时会出现两个熔融峰;但是当升温速率足够大时,在结晶不完善的聚酯开始熔化的同时温度迅速升高,熔化情况与温度出现延迟效应,使得结晶完善部分和结晶不完善部分几乎同时进行熔化过程,所以熔融过程中只出现1个熔融峰。
|
图 4 不同升温速率下的熔点测试结果 Fig.4 Melting point test results with different heating rates |
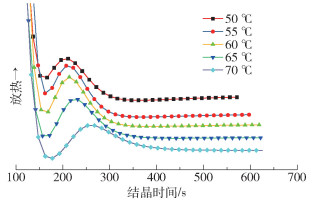
在50、55、60、65、70 ℃下不饱和结晶低熔点聚酯的等温结晶情况如图 5所示。结晶温度为50 ℃时,结晶峰宽约为120 s,出峰时间约为166 s;而结晶温度为70 ℃时,结晶峰宽约为225 s,比结晶温度为50 ℃时增加了近88%,出峰时间约为178 s,比结晶温度为50 ℃时延后了12 s。显然,随着结晶温度Tc的升高,结晶峰逐渐变宽,结晶完成所需的时间亦随着结晶温度的升高而增加。
|
图 5 不同结晶温度下的等温结晶DSC曲线 Fig.5 DSC curves of isothermal crystallization at different crystallization temperatures |
采用DSC分别测定了不饱和结晶聚酯在不同结晶温度下结晶后的熔融峰温度,结果如表 2所示。结晶温度50 ℃时的熔融峰温度为82.2 ℃,结晶温度70 ℃时的熔融峰温度为91.7 ℃,提高了约12%。可以看出随着结晶温度Tc的升高,结晶性聚酯的熔融峰温度也随之升高。
| 下载CSV 表 2 不同等温结晶温度结晶后对应的熔融峰温度 Table 2 Melting peak temperature at different isothermal crystallization temperatures |
不饱和结晶性聚酯是一种共聚物,没有特定的熔点,但是它有熔程。熔程是一个温度区间,指的是共聚物从开始熔化到完全熔融的温度范围。而且熔融温度和结晶温度之间是有关联的,结晶温度越高,熔融温度就越高。因为结晶性聚酯在结晶温度以下链段处于冻结状态,在结晶温度以上链段才可以活动。结晶是分子链的一种有序排列,熔融是将聚合物分子链的有序排列结构全部破坏掉,形成分子链形式。一般结晶度越高,分子链排列越规则,就需要更高的温度来破坏其规则的结构,故熔融温度也越高。这是因为等温结晶的温度越高,聚酯的链段越容易自我排列成规整结构,相应的结晶性聚酯最终形成的结晶相较于较低温度下的结晶更加完善,所以结晶时间更长,熔融温度亦随等温的结晶温度增大而升高。
Hoffma n-Weeks方程为
| $ {T_{\rm{m}}} = T_{\rm{m}}^0\left( {1 - \frac{1}{\eta }} \right) + \frac{{{T_{\rm{c}}}}}{\eta } $ | (1) |
式中,Tm0为平衡熔融温度;η为与晶体维数相关的常数,根据公式(1),η为Tc和Tm线性拟合直线斜率的倒数[16-17]。
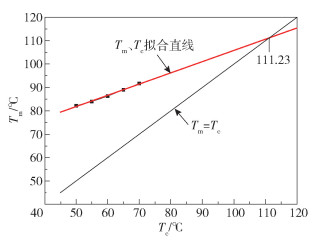
利用结晶温度Tc以及不同结晶温度下对应的熔融温度Tm作散点图,然后进行线性拟合,得到斜率为0.48、线性相关系数R2为0.99的拟合直线,可知熔融温度随着结晶温度的升高而升高,即熔融温度与结晶温度存在正相关的线性关系。当结晶温度升高至熔融温度时,此时的温度即为平衡熔融温度,从图 6可得,不饱和结晶聚酯的平衡熔融温度为111.23 ℃。
|
图 6 结晶性低熔点聚酯的平衡熔融温度 Fig.6 Equilibrium melting temperature of the crystalline low-melting polyester |
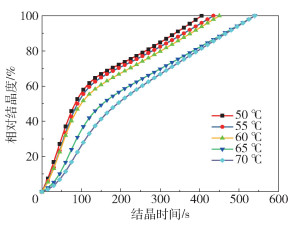
通过对不饱和结晶聚酯的等温结晶曲线积分可以得到其相对结晶度随结晶时间的变化曲线,如图 7所示。结晶温度为50 ℃时结晶完成时间约为400 s,结晶温度为70 ℃时结晶完成时间约为500 s,比结晶温度50 ℃时增加了25%。显然,结晶温度越高,相对结晶度达到100%所需的时间越长;在同一时刻,结晶温度越高,相对结晶度也越小。图 7中曲线均为“S”型,即相对结晶度开始时增大得非常快,之后速率慢慢逐渐减小,说明结晶速率是先增加到极大值,然后再慢慢减小。
|
图 7 不同结晶温度下相对结晶度随时间变化的曲线 Fig.7 Plots of relative crystallinity at different crystallization temperatures |
由于Avrami理论假设每个晶核经过无限长的时间之后,期间都是互不干扰且均匀地生长为一个结晶体[18]。这些晶体可以是棒状、圆盘或者球形,整个样品都由这些结晶体所构成。Avrami方程的一般形式为
| $ 1 - C = (\rm exp)\left( { - Z{t^n}} \right) $ | (2) |
式中,C为与时间t对应的相对结晶度;Z为结晶速率常数;t为结晶时间;n为Avrami指数[19-20]。为了方便数据分析,对Avrami方程(式(2))两边取两次对数,得到公式(3)
| $ {\rm ln}\left[ { - {\rm ln}\left( {1 - C} \right)} \right] = {\rm ln} Z + n {\rm ln} t $ | (3) |
半结晶时间t1/2计算公式为
| $ {t_{1/2}} = {\left( {{\rm ln}2/Z} \right)^{1/n}} $ | (4) |
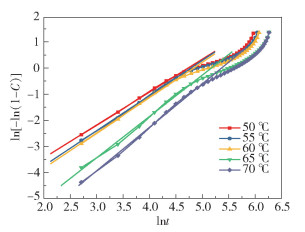
以ln[-ln(1-C)]对lnt作图,并进行线性拟合,如图 8所示,直线的斜率为n,截距为lnZ,由此可计算出结晶速率常数Z;进而利用公式(4)计算不饱和结晶聚酯的半结晶时间t1/2。
|
图 8 等温结晶的ln[-ln(1-C)]与lnt的关系曲线 Fig.8 Relationship between ln[-ln(1-C)] and lnt during isothermal crystallization |
由图 8可知,无论结晶温度高低,ln[-ln(1-C)]与lnt的关系只有部分满足线性,之后均发生了明显的偏移。前部分拟合直线的线性相关系数R2均大于0.99,线性较好。根据直线的斜率和截距以及公式(4)计算出半结晶时间t1/2,得到其主结晶的等温结晶参数,如表 3所示,n值约为1.5,说明不饱和结晶性聚酯的结晶过程为球状晶型的不依热扩散,且随着结晶温度的升高,半结晶时间增加,进一步说明结晶温度增大,结晶速率降低。
| 下载CSV 表 3 不饱和结晶低熔点聚酯的等温结晶参数 Table 3 Isothermal crystallization parameters of the unsaturated crystalline low-melting polyester |
根据两步结晶模型,结晶过程分为主结晶和二次结晶,聚合物的总结晶度为主结晶与二次结晶之和。结晶过程开始时,主结晶的结晶速率逐渐增加并达到极大值,非晶区减少,结晶速率开始减小。接着主结晶和二次结晶同时进行,直到主结晶结束后只有二次结晶,结晶速率变得非常缓慢。由于主结晶的结晶速率先增大后减小,最后只有二次结晶,结晶速率缓慢,所以图 7的相对结晶度随时间变化曲线中相对结晶度在开始时迅速增大,之后增大幅度降低,呈现类似“S”型的形状。
图 8中曲线后面的部分发生偏移,这是因为不饱和结晶性聚酯在等温结晶过程的后期发生了二次结晶,这也是当升温速率较低时DSC测试出现两个熔融峰的原因。且偏移后的曲线截距更小,由公式(4)可以明显得出偏移后的结晶速率更小,说明主结晶接近完成,几乎只有二次结晶在进行,因此结晶变得异常缓慢。
2.3.4 等温结晶过程中过冷度对结晶速率的影响结晶速率是聚合物半结晶时间的倒数,即1/t1/2;过冷度ΔTm为平衡熔融温度与结晶温度之差[21],其计算公式为
| $ \Delta {T_{\rm{m}}} = T_{\rm{m}}^0 - {T_{\rm{c}}} $ | (5) |
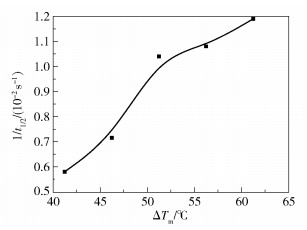
不饱和结晶性聚酯的结晶速率与对应过冷度计算结果如表 4所示,图 9为过冷度与结晶速率的关系曲线。
| 下载CSV 表 4 结晶性低熔点聚酯的过冷度和结晶速率 Table 4 Subcooling and crystallization rate of the crystalline low-melting polyester |
|
图 9 结晶性低熔点聚酯的过冷度和结晶速率的关系曲线 Fig.9 Relationship between subcooling and crystallization rate |
显然,结晶温度越高,过冷度越小。从图 9可以看出,随着过冷度的增大,结晶速率也增大,即结晶温度越大结晶速率越小。特别是在结晶温度从60 ℃升至65 ℃范围区间,结晶速率降低幅度最大,超过30%。所以为了使不饱和结晶聚酯结晶更加完善,需要较高的结晶温度,但是不能过高而造成低的结晶速率。综合考虑结晶温度选择为60 ℃,是不饱和结晶低熔点聚酯较为理想的结晶温度。
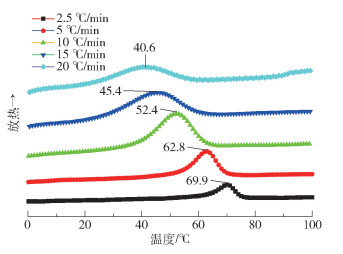
2.4 不饱和结晶性聚酯的非等温结晶行为分析 2.4.1 不同降温速率对结晶的影响不饱和结晶聚酯在不同降温速率下的DSC结晶曲线如图 10所示,通过对DSC结果进行分析,可知结晶性聚酯的开始结晶温度T0、结晶峰温度Tp、结束结晶温度T1以及对应的玻璃化转变温度Tg如表 5所示。
|
图 10 不同降温速率下的DSC结晶曲线 Fig.10 Crystallization curves with different cooling rates |
| 下载CSV 表 5 不同降温速率下不饱和结晶低熔点聚酯的结晶参数 Table 5 Crystallization parameters of the unsaturated crystalline low-melting polyester with different cooling rates |
根据图 10以及表 5的参数,可以看出降温速率从2.5 ℃/min增大至20 ℃/min时,结晶峰值温度从69.9 ℃降低到40.6 ℃,降低了近40%;结晶峰宽度从10.5 ℃增加至27.8 ℃,增加了约2倍。显然,随着降温速率的增大,结晶峰值温度逐渐下降,且结晶峰也逐渐变宽,同时不饱和结晶性聚酯的玻璃化转变温度随着降温速率的增大而减小。因为当降温速率较小时,不饱和结晶聚酯的分子链在高温段的时间较长,分子链的动能更大,拥有足够的时间来进行排列,分子链将会更加规整,结晶更加完善,使得不饱和结晶聚酯的结晶峰在较高的温度下出现,且峰型窄而尖锐。由于结晶过程与温度降低之间存在延迟,降温速率越大,聚酯结晶情况与温度降低的延迟也就越大,所以降温速率较大时,分子在高温段停留时间很短,分子来不及进行规整排列,可能温度在降低到较低温度时结晶依然在进行,因此结晶的起始温度较低,结晶峰较宽且平整。
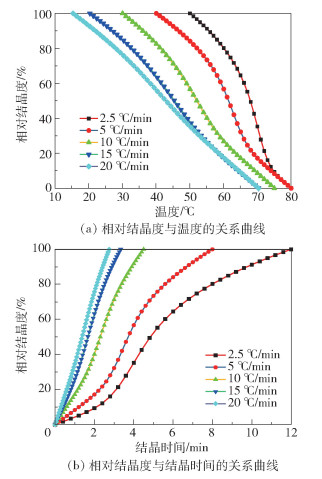
对不饱和结晶性聚酯不同降温速率下的DSC曲线进行一次积分,根据积分数据画出不同降温速率下相对结晶度与温度的关系曲线,如图 11(a)所示;再利用温度及降温速率算出相应的结晶时间,画出相对结晶度与结晶时间的关系曲线,如图 11(b)所示。从图 11可以看出,相对结晶度与温度曲线呈现反“S”型,相对结晶度与结晶时间曲线呈现“S”型,说明不饱和结晶性聚酯的非等温结晶过程也是分为两部分的。结晶速率在开始时迅速增大,随着主结晶的完成以及非晶区的减少,后期几乎只有二次结晶,结晶变得非常缓慢。图 11中当降温速率较大时,“S”型就变得不明显了,相对结晶度与时间和温度的曲线接近线性关系,这是因为降温速率较大时,温度与结晶过程的延迟较大,结晶开始进行后,温度很快就降低到玻璃化转变温度以下,使得主结晶在快速进行时因链段突然被冻结而无法继续结晶。从图中也可以看出降温速率越小,结晶与温度之间的延迟越小,链段能充分排列规整,聚酯的总体结晶更加完善,结晶完成所需要的时间也越长。
|
图 11 不同降温速率下结晶性聚酯的相对结晶度与温度和结晶时间的关系曲线 Fig.11 Variation of the relative crystallinity with temperature and crystallization time with different cooling rates |
Ozawa[22]基于Evans理论,假设晶核是在熔体中无规则随机形成的,然后再分别逐渐长大,从而推导出等速降温的聚合物结晶动力学方程
| $ 1 - C\left( T \right) = \exp \left[ { - K\left( T \right)/{\mathit{\Phi }^m}} \right] $ | (6) |
式中,C(T)为在温度T时的相对结晶度;Φ为降温速率;m为Ozawa指数;K(T)为冷却函数,是温度的函数。对Ozawa方程(6)两边取两次对数,得到公式(7)
| $ \lg \left\{ { - \ln \left[ {1 - C\left( T \right)} \right]} \right\} = \lg K\left( T \right) - m\lg \mathit{\Phi } $ | (7) |
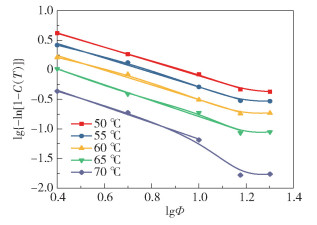
在同一温度下,以lg{-ln[1-C(T)]}对lgΦ作图,得到如图 12所示的曲线,然后对曲线进行线性拟合,得到拟合直线的斜率即为Ozawa指数m,截距为冷却函数K(T),具体数据见表 6。
|
图 12 结晶性聚酯的lg{-ln[1-C(T)]}与lgΦ关系曲线 Fig.12 Relationship curves between lg{-ln[1-C(T)]}and lgΦ of the crystalline polyester |
| 下载CSV 表 6 根据Ozawa法得到的不同降温速率下的动力学参数 Table 6 Kinetic parameters for different cooling rates based on the Ozawa method |
对表 6中由Ozawa法得出的参数进行分析,线性拟合的相关系数R2不低于0.98,说明线性相关性很好,不饱和结晶性聚酯的Ozawa指数在降温速率较小时随着温度的升高而逐渐增大,冷却函数与之相反,随着温度的升高而减小。但是图 12中当降温速率较大时,曲线发生了偏离。这是由于Ozawa方程是利用同一温度下的不同降温速率和相对结晶度来进行分析,当降温速率较大时就类似于等温结晶中过冷度很大时结晶速率较高的情况,对应于结晶过程的后期,而降温速率较小时,则对应于结晶过程的初期。但是对于非等温结晶过程,从图 11中可以看出结晶前期和后期的差别很大,所以lg{-ln[1-C(T)]}对lgΦ作图在后期发生偏离,故而Ozawa法不适于不饱和结晶性聚酯的非等温结晶动力学分析。
2.4.3 非等温结晶动力学的Jeziorny法分析与Ozawa法不同,Jeziorny法是将等温结晶Avrami方程应用于非等温结晶行为的分析,即直接将非等温结晶DSC结晶曲线及数据当作是等温结晶过程来进行处理,再对分析得到的参数进行修正[23],公式如下
| $ \ln \left\{ { - \ln \left[ {1 - C\left( T \right)} \right]} \right\} = \ln Z + n\ln t $ | (8) |
考虑到降温速率Φ的影响,对结晶速率常数Z进行校正
| $ \lg {Z_{\rm{c}}} = \frac{{\lg Z}}{\mathit{\Phi }} $ | (9) |
相应的半结晶时间公式为
| $ {t_{1/2}} = {\left( {\ln 2/{Z_{\rm{c}}}} \right)^{1/n}} $ | (10) |
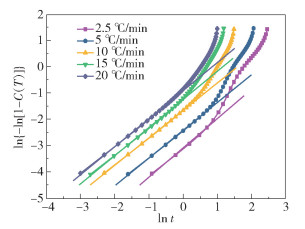
根据方程(8),以ln{-ln[1-C(T)]}对lnt作图,如图 13所示。显然在整个结晶区间内,曲线并不具备线性关系,曲线中间有明显的转折点,前部分符合线性关系,转折点之后曲线发生了偏移,再次说明不饱和结晶性聚酯存在二次结晶。曲线的转折点可以作为主结晶的线性部分和二次结晶的非线性部分的分界点[24]。二次结晶时,由于主结晶已经基本完成,非晶区减小即链段活动区间变小,晶体生长受到阻碍,因此采用Jeziorny法分析曲线的后期会发生严重偏移。而且从图中还可以看出降温速率越小的结晶性聚酯,结晶更加完善,非晶区越小,所以偏移程度越大。
|
图 13 结晶性聚酯的ln{-ln[1-C(T)]}与lnt的关系曲线 Fig.13 Relationship between ln{-ln[1-C(T)]} and lnt for the crystalline polyester |
对图 13中的部分曲线进行线性拟合,线性相关系数R2>0.99,说明主结晶部分的线性很好。根据拟合直线的斜率求出Avrami指数n,根据直线的斜率求出速率常数Zc,得到不同降温速率下的结晶动力学参数列于表 7中。对表 7的数据分析可知,非等温结晶的Avrami指数n约为1,修正后的结晶速率常数Zc随着降温速率从2.5 ℃/min增大至20 ℃/min而从0.290增大到0.955,增加了230%,说明降温速率越大,半结晶时间越短,结晶性聚酯的结晶速率越大。
| 下载CSV 表 7 根据Jeziorny法获得的不同降温速率下的动力学参数 Table 7 Kinetic parameters for different cooling rates obtained by the Jeziorny method |
由于Ozawa法是针对一定温度下相对结晶度与降温速率的关系,降温速率的种类一般较少,如本文采用5种不同降温速率,得到5组数据,获取的原始数据较少,拟合出的线性关系不够精准;而Jeziorny法是针对相对结晶度与时间的关系,其获得的Avrami指数n往往不能准确地判断结晶聚合物的非等温结晶过程,物理意义不大。
莫志深[25]在Ozawa法和Jeziorny法的基础上,提出了一种新的对聚合物非等温结晶动力学进行分析的有效方法,主要是针对于降温速率和结晶时间的关系,因为在某一相对结晶度下,必定有其对应的降温速率和结晶时间,由此推导出了新的方程
| $ \lg \mathit{\Phi } = \lg F\left( T \right) - a\lg t $ | (11) |
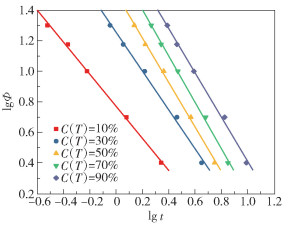
式中,a=n/m,n为非等温结晶过程中的Avrami指数,m为Ozawa指数;F(T)可用来表征聚合物结晶的快慢,其物理意义为某一体系在单位时间内达到某一相对结晶度时必须选取的冷却(或加热)的速率值。以lgΦ对lgt作图,可以得到一系列直线,如图 14所示。通过直线的截距可以求得F(T),通过斜率可以得到a,计算得到的参数列于表 8。
|
图 14 结晶性聚酯的lgΦ与lg t的关系曲线 Fig.14 Plots of lgΦ against lgt for the crystalline polyester |
| 下载CSV 表 8 根据Mo法获得的不同降温速率下的动力学参数 Table 8 Kinetic parameters for different cooling rates obtained by the Mo method |
表 8中的线性相关系数R2均大于0.99,可知lgΦ和lgt之间具有良好的线性相关性,说明Mo法适用于不饱和结晶性聚酯的非等温结晶动力学分析。从表中的数据规律分析,相对结晶度为10%时,F(T)为0.77,相对结晶度增大到90%,F(T)增大到1.86,增加了140%,说明相对结晶度越大,结晶越困难,需要更大的降温速率。这与前面Jeziorny法分析的结果相吻合,即结晶度越大,非晶区越小,不饱和结晶性聚酯随着结晶过程的进行结晶越困难。
2.5 不同结晶温度对不饱和结晶性聚酯结晶形貌的影响从图 15(b)中可明显看出不饱和结晶聚酯在偏光显微镜下出现十字消光现象,而图 15(a)中的消光十字大小均相等,说明结晶性聚酯的晶型为球晶,成核方式为不依热成核,所有的晶核几乎均在同一时间形成并开始生长。证实了2.3节等温结晶动力学分析中的结论,即Avrami指数n的值约为1.5时,其晶体形状为球晶,结晶过程为不依热的扩散。

|
图 15 不饱和结晶性聚酯不同结晶温度下的结晶形貌 Fig.15 Crystal morphology of the unsaturated crystalline polyester at different crystallization temperatures |
通过标准片的对比,计算出结晶温度为50 ℃时,球晶的直径约为11 μm,结晶温度为55 ℃时,球晶直径约为18 μm,结晶温度为60 ℃时球晶直径为22 μm,相比结晶温度为50 ℃时增大了一倍。说明不饱和结晶性聚酯结晶的时间相同时,结晶温度较低的聚酯球晶尺寸较小,结晶不够完善;而结晶温度较高得到的球晶直径较大,结晶较完善,相应地在较高的温度下才可以完全熔化,所以结晶温度较高的不饱和结晶性聚酯熔点也较高。
3 结论(1) 通过DSC以不同的升温速率测试不饱和结晶性聚酯的熔点,结果表明升温速率较小时有两个熔融峰,随着升温速率的增大,两个熔融峰逐渐靠近,在30 ℃/min的升温速率下测试得到不饱和结晶聚酯只有一个熔融峰,熔点为93.5 ℃。
(2) 研究了不同温度下不饱和结晶性聚酯的等温结晶情况并采用Avrami方程对其等温结晶动力学进行了分析,结果表明不饱和结晶性聚酯的结晶过程存在二次结晶,随着结晶温度的升高,半结晶时间延长,结晶速率降低。为了兼顾结晶速率和结晶情况,选择60 ℃的结晶温度较为理想。且Avrami指数n约为1.5,通过偏光显微镜也观察到大小相等的十字消光现象,说明结晶性低熔点聚酯的结晶过程为球状晶型的不依热扩散。
(3) 采用Ozawa法、Jeziorny法以及Mo法分别对不饱和结晶性聚酯进行了非等温结晶动力学分析,对比发现Jeziorny法和Mo法均适用于不饱和结晶性聚酯的非等温结晶动力学的分析。Jeziorny法和Mo法的分析结果表明:不饱和结晶性聚酯的结晶过程由主结晶和二次结晶组成,体系的降温速率越大,半结晶时间越短,聚酯的结晶速率越大,且随着不饱和结晶性聚酯相对结晶度的增大,结晶变得越来越困难。
| [1] |
王立岩, 王菲, 徐大志. 低熔点共聚酯的研究进展[J]. 合成纤维, 2015, 44(12): 1-4. WANG L Y, WANG F, XU D Z. Development of low melting point copolyesters[J]. Synthetic Fiber in China, 2015, 44(12): 1-4. (in Chinese) |
| [2] |
沈开猷. 不饱和聚酯树脂及其应用[M]. 3版. 北京: 化学工业出版社, 2005: 1-15. SHEN K Y. Unsaturated polyester resin and its application[M]. 3rd ed. Beijing: Chemical Industry Press, 2005: 1-15. (in Chinese) |
| [3] |
孙小甫. PET共聚酯的制备及液相增黏研究[D].杭州: 浙江理工大学, 2018. SUN X F. Study on preparation and liquid-state polycondensation of PET copolyester[D]. Hangzhou: Zhejiang Sci-Tech University, 2018. (in Chinese) |
| [4] |
陈延明, 李英, 李承媛, 等. 低熔点PBT共聚酯的制备及其熔融结晶行为分析[J]. 合成纤维工业, 2017, 40(6): 38-42. CHEN Y M, LI Y, LI C Y, et al. Preparation and melting crystallization behavior of low-melting point PBT copolyesters[J]. China Synthetic Fiber Industry, 2017, 40(6): 38-42. (in Chinese) |
| [5] |
JOSHI M D, LONIKAR S V, MALDAR N N. Synthesis and characterization of silicon-containing poly(amide-amide)s[J]. Journal of Applied Polymer Science, 2001, 79: 1610-1617. |
| [6] |
王慧, 邹林, 刘小峯. 2016-2017年国内外不饱和聚酯树脂工业进展[J]. 热固性树脂, 2018, 33(3): 56-64. WANG H, ZOU L, LIU X F. International industry development of unsaturated polyester resin from 2016 to 2017[J]. Thermosetting Resin, 2018, 33(3): 56-64. (in Chinese) |
| [7] |
刘小峯, 王秀玲, 邹林. 2017-2018年国内外不饱和聚酯树脂工业进展[J]. 热固性树脂, 2019, 34(3): 61-70. LIU X F, WANG X L, ZOU L. Development of unsaturated polyester resin industry at home and abroad from 2017 to 2018[J]. Thermosetting Resin, 2019, 34(3): 61-70. (in Chinese) |
| [8] |
张文军, 朱春宇. 不饱和聚酯树脂改性研究进展[J]. 热固性树脂, 2007, 22(4): 41-46. ZHANG W J, ZHU C Y. Advances in modification of unsaturated polyester resin[J]. Thermosetting Resin, 2007, 22(4): 41-46. (in Chinese) |
| [9] |
邹多福, 伍凯飞. 低熔点聚酯的开发与应用概况[J]. 科研与生产, 2018(1/2): 3-5. ZOU D F, WU K F. Development and application of low melting polyester[J]. Research and Production, 2018(1/2): 3-5. (in Chinese) |
| [10] |
JING X K, GUO D M, ZHANG J B, et al. Thermal transition behavior, thermal stability, and flame retardancy of low-melting-temperature copolyester:comonomer effect[J]. Industrial and Engineering Chemistry Research, 2013, 52(12): 4539-4546. |
| [11] |
许小强, 周权, 倪礼忠, 等. 结晶性不饱和聚酯的合成及其流变行为的研究[J]. 热固性树脂, 2016, 31(6): 28-31. XU X Q, ZHOU Q, NI L Z, et al. Study on the synthesis and rheological behavior of the crystalline unsaturated polyester[J]. Thermosetting Resin, 2016, 31(6): 28-31. (in Chinese) |
| [12] |
赵萍.二甘醇对改性PET共聚酯热熔胶熔融及结晶行为影响的研究[D].上海: 华东理工大学, 2014. ZHAO P. Study on the effect of diethylene glycol on the melting and crystallization behavior of PET copolyester hot-melt adhesive[D]. Shanghai: East China University of Science and Technology, 2014. (in Chinese) |
| [13] |
王赛博.结晶性低熔点聚酯及其纤维的制备研究[D].上海: 东华大学, 2016. WANG S B. The preparation and research of crystalline low melting point polyester fibers[D]. Shanghai: Donghua University, 2016. (in Chinese) |
| [14] |
黄志雄, 李建, 梅启林, 等. 低压片状模塑料用结晶不饱和聚酯树脂的合成[J]. 粘接, 2005, 26(3): 1-3. HUANG Z X, LI J, MEI Q L, et al. Synthesis of crystalline unsaturated polyester for low pressure SMC[J]. Adhesion in China, 2005, 26(3): 1-3. (in Chinese) |
| [15] |
中华人民共和国化学工业部.聚酯多元醇中酸值的测定: HG/T2708-1995[S]. 1996-01-01. Ministry of Chemical Industry of the People's Republic of China. Determination of acid value in polyester polyols: HG/T2708-1995[S]. 1996-01-01. (in Chinese) |
| [16] |
WENG W G, CHEN G H, WU D J. Crystallization kinetics and melting behaviors of nylon 6/foliated graphite nanocomposites[J]. Polymer, 2003, 44(26): 8119-8132. |
| [17] |
HOFFMAN J D, WEEKS J J. Melting process and the equilibrium melting temperature of poly(chlorotrifluoroethylene)[J]. Journal of Research of the National Bureau of Standards, Section A:Physics and Chemistry, 1962, 66. |
| [18] |
莫志深. 高分子结晶和结构[M]. 北京: 科学出版社, 2017: 270-283. MO Z S. Polymer crystallization and structure[M]. Beijing: Science Press, 2017: 270-283. (in Chinese) |
| [19] |
AVRAMI M. Kinetics of phase change. I. General theory[J]. Journal of Chemical Physics, 1939, 7: 1103-1112. |
| [20] |
AVRAMI M. Kinetics of phase change. Ⅱ. Transformation-time relations for random distribution of nuclei[J]. Journal of Chemical Physics, 1940, 8: 212-224. |
| [21] |
徐勇. PTT及其共聚酯的合成与结晶行为研究[D].杭州: 浙江大学, 2005. XU Y. The study of synthesis and crystallization behavior of PTT and its copolyesters[D]. Hangzhou: Zhejiang University, 2005. (in Chinese) |
| [22] |
OZAWA T. Non-isothermal kinetics of diffusion and its application to thermal analysis[J]. Journal of Thermal Analysis, 1973, 5(5/6): 563-576. |
| [23] |
JEZIORNY A. Parameters characterizing the kinetics of the non-isothermal crystallization of poly(ethylene terephthalate) determined by d.s.c.[J]. Polymer, 1978, 19(10): 1142-1144. |
| [24] |
张声春, 韩冰, 张春祥, 等. 半芳香共聚尼龙6T/6的非等温结晶动力学研究[J]. 塑料工业, 2013, 41(11): 91-94. ZHANG S C, HAN B, ZHANG C X, et al. Nonisothermal crystallization kinetics of semi-aromatic co-polyamide 6T/6[J]. China Plastics Industry, 2013, 41(11): 91-94. (in Chinese) |
| [25] |
莫志深. 一种研究聚合物非等温结晶动力学的方法[J]. 高分子学报, 2008(7): 656-661. MO Z S. A method for the non-isothermal crystallization kinetics of polymers[J]. Acta Polymerica Sinica, 2008(7): 656-661. (in Chinese) |








