多智能体系统(multi-agent system,MAS)目前主要应用于飞行编队、信号控制等领域,其思想源于自然界中的编队现象。多智能体系统的特殊性在于,每个智能体都能根据给出的全局目标进行自主规划,通过智能体之间的交流达到解决问题的目的,使得复杂系统的表达得到简化。哈佛大学自组织研究所设计了一个名为Kilobot的简单低成本机器人[1-2],由若干个机器人组成的小型群体可以在平面上执行一系列简单的多智能体行为。Kilobot机器人群体的面世使得多智能体系统在实际生活中的应用成为可能。
蜂拥算法(flocking algorithm)是一应用广泛且性能良好的多智能体算法。Reynolds[3]于1987年在其模拟程序Boids中首次模拟了多智能体的蜂拥行为。随后科研人员们就控制算法[4-5]、机器人[6-7]、移动传感网络[8-9]等方面都进行了大量研究。其中,王帅磊等[4]提出了基于Levy飞行的蜂拥控制算法,采用Levy飞行策略对目标进行搜索,在移动智能体群体中加入搜索智能体,智能体根据周围邻居和感知到的目标信息调整自身运动;潘无为等[7]针对多自主式水下机器人(AUV)系统,设计了一种结合人工势场与虚拟结构的多AUV编队控制算法,可令AUV系统无碰撞地进行编队变换;娄柯等[8]构造了一个虚拟的领导者节点,可令其他网络各节点作为跟随者,跟踪领导者的运动轨迹,实现了网络拓扑结构连通性的保持。基于前人的成熟的研究成果可知,多智能体蜂拥算法能够良好地应用于实际生活。
现今有众多手部结构完整但活动不便的患者,已有研究人员为该类患者设计了不需要与人体神经对接的外骨骼系统[10],它通过传感器感应人手的肌肉运动意图,外接机械系统通过杠杆产生目标需要的作用力,以此帮助患者进行正常的手部运动。
然而,传统的机械手系统结构固定,不易于根据患者手的大小不同灵活变换。由于多智能体系统具有易于更换且能够自主规划的特性,可考虑运用多智能体系统辅助患者的运动;同时,作为多智能体算法中的蜂拥算法可实现多智能体的自组织功能。因此对蜂拥算法进行改进,使其能够适配于人体手指的运动,从而辅助患者进行日常的手部活动是一种可行的思路。
本文于Unity引擎内模拟了均匀安装在手指上的若干智能体单元组成的多智能体系统追随目标点的运动行为,并带动手指以辅助手指弯曲的过程。基于多智能体原理制作辅助手部运动系统是一个崭新的思想,该系统可灵活改变智能体的大小和数目,且无需为每个智能体分别设置不同的算法或目标,为今后做出辅助系统的实体提供了可行的理论依据。
1 蜂拥算法基础蜂拥算法由以下3个规则控制[3]:
(1) 分离智能体与邻域内其他智能体避免碰撞;
(2) 聚合智能体对邻域内其他智能体具有吸引力;
(3) 匹配智能体与其他智能体保持速度相同。
采用Olfati-Saber[11]设计的单虚拟领导者的蜂拥算法。该算法主要基于势能函数原理和一致性原理。在算法中,假设全部智能体都能接收到虚拟领导目标点的信息。
1.1 势能函数基于势能函数的蜂拥算法的主要思想是在智能体周围模拟类似于原子之间的吸引力场和排斥力场,使得系统在稳定状态时能够实现基础蜂拥算法中的分离和聚合规则。文献[11]中提出的势能函数如式(1)所示。
| $ {\psi _\alpha }\left( z \right) = \int_{{d_\alpha }}^z {{\phi _\alpha }} \left( s \right){\rm{d}}s $ | (1) |
式中,
| $ {\phi _\alpha }\left( z \right) = {\rho _h}\left( {z/{r_\alpha }} \right)\phi \left( {z/{d_\alpha }} \right) $ | (2) |
| $ \begin{array}{l} \phi \left( z \right) = \frac{1}{2}\left[ {\left( {a + b} \right)\left( {z + k} \right)/\sqrt {1 + {{\left( {z + k} \right)}^2}} } \right. + \\ \left. {\left( {a - b} \right)} \right] \end{array} $ | (3) |
| $ {\rho _h}\left( z \right) = \left\{ {\begin{array}{*{20}{l}} {1,}&{z \in \left[ {0,h} \right)}\\ {\frac{1}{2}\left\{ {1 + cos\left[ {{\rm{ \mathsf{ π} }}\frac{{z - h}}{{1 - h}}} \right]} \right\},}&{z \in \left[ {h,1} \right]}\\ {0,}&{其他} \end{array}} \right. $ | (4) |
式中,a、b、k、h为常数;rα(rα>0)为传感器能够感知的范围;dα(dα>0)为智能体之间需要保持的距离。
1.2 一致性原理多智能体系统中,智能体系统的状态方程式为
| $ {{\mathit{\boldsymbol{\dot x}}}_i}\left( t \right) = {\mathit{\boldsymbol{u}}_i}\left( t \right) $ | (5) |
式中,xi(t)∈
| $ {\mathit{\boldsymbol{u}}_i}\left( t \right) = \mathit{\boldsymbol{L}}\left( t \right)\mathit{\boldsymbol{x}}\left( t \right) = \sum\limits_{j \in {N_i}} {{\mathit{\boldsymbol{a}}_{ij}}\left( t \right)\left[ {{\mathit{\boldsymbol{x}}_j}\left( t \right) - {\mathit{\boldsymbol{x}}_i}\left( t \right)} \right]} $ | (6) |
式中,L(t)为无权无向图的拉普拉斯矩阵,aij(t)为网络时刻的邻接矩阵。
线性一致算法控制了智能体系统的稳定性,使得智能体的速度保持一致,可实现基础蜂拥算法中的匹配规则。
2 模型建立与仿真Unity是利用交互式图型化开发环境为首要方式的引擎,能较便捷地创作三维模型。本实验将在Unity引擎内进行模拟。其中,人体手部骨骼模型使用Unity Assets Store中的Hand Physics Controller模型,该模型是一节具有手腕的左手,手指的各个关节可自由活动,其中中指长度为1 190像素。假设在现实中系统外部有类似手套的载体,由于载体具有一定的弹性系数,故在此次模拟中通过弹簧关节(spring joint)来模拟实现载体的作用。
于Unity引擎中创建80个完全相同的球形智能体,智能体直径为100像素。将所有智能体通过弹簧关节均匀地固定在左手模型的5根手指上,每根手指分配到16个智能体(手指的上表面与下表面均放置8个),智能体之间间隔150像素。智能体的运动遵循蜂拥算法。为每根手指上的16个智能体分别设立1个目标点,目标点的位置可通过鼠标拖动随时更改。目标点所在位置即代表着患者的运动目的。
初始状态的手部模型如图 1所示。

|
图 1 智能体在手部分布情况 Fig.1 Agent distribution on a hand |
由于单根手指上多智能体系统的智能体个数为16,系统的运动方程[11]可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot q}}}_i}\left( t \right) = {\mathit{\boldsymbol{p}}_i}\left( t \right)}\\ {{{\mathit{\boldsymbol{\dot p}}}_i}\left( t \right) = {\mathit{\boldsymbol{u}}_i}\left( t \right)} \end{array}} \right.\;\;\;\;\;\;i = 1,2, \cdots ,16 $ | (7) |
式中,qi(t)∈
系统虚拟目标点的运动方程[11]为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot q}}}_\gamma }\left( t \right) = {\mathit{\boldsymbol{p}}_\gamma }\left( t \right)}\\ {{{\mathit{\boldsymbol{\dot p}}}_\gamma }\left( t \right) = {\mathit{\boldsymbol{u}}_\gamma }\left( t \right)} \end{array}} \right. $ | (8) |
式中,qγ(t)∈
| $ {\mathit{\boldsymbol{u}}_i}\left( t \right) = \mathit{\boldsymbol{u}}_i^\alpha \left( t \right) + \mathit{\boldsymbol{u}}_i^\beta \left( t \right) + \mathit{\boldsymbol{u}}_i^\gamma \left( t \right) $ | (9) |
式中,
| $ \begin{array}{l} \mathit{\boldsymbol{u}}_i^\alpha \left( t \right) = \sum\limits_{j \in {N_i}} {{\phi _\alpha }\left[ {{{\left\| {{\mathit{\boldsymbol{q}}_j}\left( t \right) - {\mathit{\boldsymbol{q}}_i}\left( t \right)} \right\|}_\sigma }} \right]} \times \\ \frac{{{\mathit{\boldsymbol{q}}_j}\left( t \right) - {\mathit{\boldsymbol{q}}_i}\left( t \right)}}{{\sqrt {1 + \sigma {{\left\| {{\mathit{\boldsymbol{q}}_j}\left( t \right) - {\mathit{\boldsymbol{q}}_i}\left( t \right)} \right\|}^2}} }} \end{array} $ | (10) |
| $ \mathit{\boldsymbol{u}}_i^\beta \left( t \right) = \sum\limits_{j \in {N_i}} {{\mathit{\boldsymbol{a}}_{ij}}\left( t \right)\left[ {{\mathit{\boldsymbol{p}}_j}\left( t \right) - {\mathit{\boldsymbol{p}}_i}\left( t \right)} \right]} $ | (11) |
| $ \begin{array}{l} \mathit{\boldsymbol{u}}_i^\gamma \left( t \right) = - {c_1}\left[ {{\mathit{\boldsymbol{q}}_i}\left( t \right) - {\mathit{\boldsymbol{q}}_\gamma }\left( t \right)} \right] - {c_2}\left[ {{\mathit{\boldsymbol{p}}_i}\left( t \right) - } \right.\\ \left. {{\mathit{\boldsymbol{p}}_\gamma }\left( t \right)} \right] \end{array} $ | (12) |
| $ {\left\| z \right\|_\sigma } = \frac{{\sqrt {1 + \sigma {{\left\| z \right\|}^2}} - 1}}{\sigma } $ | (13) |
式中,c1、c2、σ为常数项;uiα(t)与uiβ(t)均为控制势能函数,其中uiα(t)实现基础蜂拥算法中的分离规则和聚合规则,uiβ(t)控制速度一致,实现匹配规则,uiγ(t)为多智能体系统的虚拟领导者导航反馈量,可诱导整个系统都跟随虚拟领导者运动,最终实现蜂拥效果。
2.1.2 算法改进原始蜂拥算法主要解决开放空间内的多智能体目标追踪问题,但安装在手指表面的智能体受到手部结构的限制,无法在空间中自由移动。正常手指弯曲时,手指尖端的弯曲幅度明显大于手指根部。针对手指这一特性作出算法改进,将手指根部的位置矢量表示为qroot。首先将式(11)中的速度匹配项改进为
| $ \mathit{\boldsymbol{u}}_i^\beta \left( t \right) = \sum\limits_{j \in {N_i}} {{\mathit{\boldsymbol{a}}_{ij}}\left( t \right)\left[ {{\mathit{\boldsymbol{p}}_j}\left( t \right)\frac{{{\mathit{\boldsymbol{q}}_i}\left( t \right) - {\mathit{\boldsymbol{q}}_{{\rm{root}}}}}}{{{\mathit{\boldsymbol{q}}_j}\left( t \right) - {\mathit{\boldsymbol{q}}_{{\rm{root}}}}}} - {\mathit{\boldsymbol{p}}_i}\left( t \right)} \right]} $ | (14) |
由于原文中已知所有控制点的原速度矢量pi(t)和原位置矢量qi(t),通过pi(t)及qi(t)可计算出即时的加速度矢量ui(t)。现在加入一个远离系数ω,通过智能体到手指根部的距离之比计算出智能体当前状态的实时速度矢量p′ i(t)。以手指中点的速度为基准,用qmid表示手指中点的位置矢量,则改进后智能体的速度矢量p′ i(t)可以表示为
| $ {{\mathit{\boldsymbol{p'}}}_i}\left( t \right) = {\mathit{\boldsymbol{p}}_i}\left( t \right) + \omega {\mathit{\boldsymbol{u}}_i}\left( t \right)\Delta t\frac{{\left| {{\mathit{\boldsymbol{q}}_i}\left( t \right) - {\mathit{\boldsymbol{q}}_{{\rm{root}}}}} \right|}}{{\left| {{\mathit{\boldsymbol{q}}_{{\rm{mid}}}} - {\mathit{\boldsymbol{q}}_{{\rm{root}}}}} \right|}} $ | (15) |
可通过调整ω的值来改变手指的运动速度。在本文实验中,ω的值设置为1。
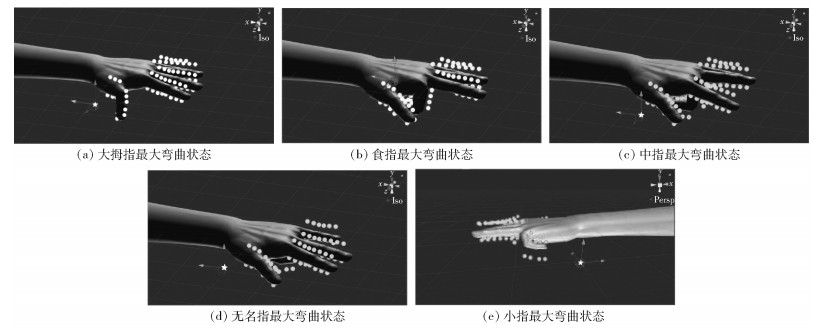
2.2 仿真实验结果启动基于改进蜂拥算法的多智能体系统后,白色的球形智能体群体便会跟随目标点作蜂拥算法控制的自组织运动,将手逐渐带动至目标点。在系统中,目标点用白色五角星标示(图 2)。
|
图 2 5根手指的弯曲示意图 Fig.2 Bending states of the five fingers |
通过移动虚拟目标点的位置,可令所有手指弯曲。在手指运动的可达范围内,目标点越往远离手的方向移动,手指弯曲程度越大。移动目标点后,5根手指的弯曲示意如图 2所示。
由图 2可见,5根手指都能通过移动目标点实现不同程度的弯曲,并最终达到某一阈值。通过5根手指的共同作用,可令整个左手实现抓握物体等动作。
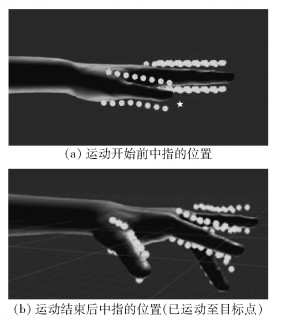
3 实验结果分析 3.1 结果分析以中指上的16个智能体为例,将目标点设置在中指可到达的位置(图 3(a)),此时目标点的坐标为(-300, -450, 0)。取时间间隔Δt=0.1 s来记录16个智能体向目标点运动过程中的即时位置和即时速度。中指开始运动和结束运动时的状态如图 3所示。
|
图 3 中指开始运动和结束运动时的状态 Fig.3 The position of the middle finger before and after the motion |
由于中指弯曲主要是在xy平面上发生位置变化,在z轴上几乎没有位置变化,故分析时只需提取出智能体在x轴及y轴上的即时位置情况。
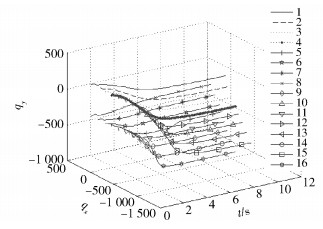
由图 4可以看出,16个智能体相对手指的位置不同,故到达目标点的时间也不尽相同;智能体的移动轨迹都较为平滑、连续,不易伤害到人体,故认为今后将该系统做成实体是可行的。
|
图 4 智能体在xy平面的位置随时间变化情况 Fig.4 Variation of the agent in the xyplane with time |
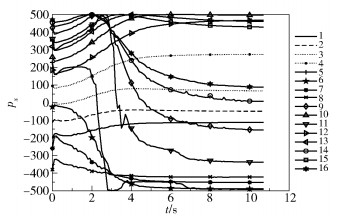
随后,提取出智能体速度在x、y、z轴上的分量。从图 5中可以看出,智能体在x轴上的速度分量相对均衡,在t=2 s及t=6 s之间呈现出比较大的速度变化,在t=8 s时手指本身不再位移,此时认为系统达到了稳态。判断出系统达到稳态后,智能体将在2 s的延迟后自动停止运动。
|
图 5 智能体速度在x轴的分量 Fig.5 The component of the speed of the agent on the x-axis |
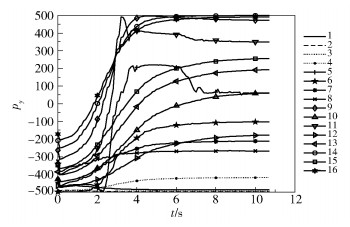
由于中指主要向y轴的负半轴弯曲,故图 6中智能体速度在y轴的分量于t=2 s时呈现出加速度向上的态势,原因在于系统阻止中指的迅速向下运动,使中指较为平滑地进行向下弯曲的动作;同样在t=8 s时系统大致达到了稳态。
|
图 6 智能体速度在y轴的分量 Fig.6 The component of the speed of the agent on the y-axis |
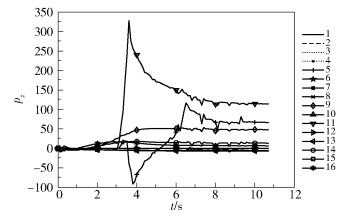
z轴方向上手指没有任何位移,故图 7中智能体在z轴上的速度分量图像基本上是围绕pz=0进行轻微震动。但图中有两条曲线(5号曲线与11号曲线)代表的智能体速度相对突出。5号曲线对应位于中指关节上方的智能体,而11号曲线对应位于中指关节下方的智能体。在手指关节处的智能体随着手部运动有一定的偏移量是正常表现,具体如何减少该偏移量还需今后进一步的研究和分析。
|
图 7 智能体速度在z轴的分量 Fig.7 The component of the speed of the agent on the z-axis |
选取编号从1到9共9个位置的目标点(图 8)来测试系统达到稳定所需时间。测试结果见表 1。

|
图 8 灵敏度测试 Fig.8 Sensitivity test |
| 下载CSV 表 1 目标点的坐标及其达到稳定所需时间 Table 1 The coordinates of the target point and the time it takes to stabilize |
从表 1中可以看出,算法改进后较改进前系统达到稳定所需时间明显缩短,从而可认为改进后的蜂拥算法可以更好地匹配人体手指。同时,当y轴坐标固定在-300时,目标点越远离指尖,手指弯曲幅度越大,故系统达到稳态所需时间越长,此时手指完全弯曲所需时间约为18 s;而当x坐标固定在-300时,由于目标点离指尖的远近变化并没有太多地影响到手指的弯曲程度,故运动时长也无明显变化,基本稳定在8 s左右。可见该系统的运动时长主要与手指弯曲幅度有关。
4 结论(1) 使用改进的蜂拥算法建立并仿真了一个多智能体手部运动辅助系统,通过多个智能体的运动带动手指运动,最终实现患者的运动意图。
(2) 本文智能体系统只需为所有智能体设置相同的算法,当设置好目标点后,所有智能体便可自适应调整自己的运动速度和运动方向,直至抵达目标点。故当单个智能体损坏时可随时更换,硬件上容错率较高。
(3) 本文智能体的数目可在一定范围内改变,可根据不同大小的手设置不同数目的智能体,拥有较高的灵活性。
(4) 基于本文模拟所用的参数,系统的运动时长约在7~18 s之间,运动轨迹平滑、连续,可认为该系统具有一定的安全性。该系统可根据患者手的大小调整智能体的个数及振动强度,并且可随时更换出故障的智能体,操作灵活,为多智能体系统的应用提供了崭新的思路。
目前已有现成的传感器,及现成的可运用多智能体算法的小型智能体,故今后将该系统做成实体是可行的。今后需要考虑调整传感器的测定方式,智能体的运动方式,以及找到合适的智能体的安装载体(如软性手套等)。
| [1] |
RUBENSTEIN M, CORNEJO A, NAGPAL R. Programmable self-assembly in a thousand-robot swarm[J]. Science, 2014, 345(6198): 795-799. DOI:10.1126/science.1254295 |
| [2] |
RUBENSTEIN M, AHLER C, NAGPAL R. Kilobot: a low cost scalable robot system for collective behaviors[C]//2012 IEEE International Conference on Robotics and Automation. Saint Paul, 2012: 3293-3298.
|
| [3] |
REYNOLDS C W. Flocks, herds and schools: a distrib-uted behavioral model[C]//ACM Siggraph Computer Graphics. New York: Association for Computing Ma-chinery, 1987, 21(4): 25-34.
|
| [4] |
王帅磊, 张金春, 曹彪, 等. 基于Levy飞行的蜂拥控制算法在目标跟踪中的应用[J]. 兵工自动化, 2016, 35(7): 35-40. WANG S L, ZHANG J C, CAO B, et al. Application in target tracking of flocking control algorithm based on Levy flight[J]. Ordnance Industry Automation, 2016, 35(7): 35-40. (in Chinese) DOI:10.7690/bgzdh.2016.07.009 |
| [5] |
钟午, 张伟, 康怀褀, 等. 一种改进的多领导者蜂拥算法及其性能分析[J]. 小型微型计算机系统, 2014, 35(9): 2116-2121. ZHONG W, ZHANG W, KANG H Q, et al. An improved flocking algorithm with multiple leaders and its performance analysis[J]. Journal of Chinese Computer Systems, 2014, 35(9): 2116-2121. (in Chinese) DOI:10.3969/j.issn.1000-1220.2014.09.035 |
| [6] |
JIA Y N, WANG L. Experimental implementation of distributed flocking algorithm for multiple robotic fish[J]. Control Engineering Practice, 2014, 30: 1-11. DOI:10.1016/j.conengprac.2014.05.004 |
| [7] |
潘无为, 姜大鹏, 庞永杰, 等. 人工势场和虚拟结构相结合的多水下机器人编队控制[J]. 兵工学报, 2017, 38(2): 326-334. PAN W W, JIANG D P, PANG Y J, et al. A multi-AUV formation algorithm combining artificial potential field and virtual structure[J]. Acta Armamentarii, 2017, 38(2): 326-334. (in Chinese) DOI:10.3969/j.issn.1000-1093.2017.02.017 |
| [8] |
娄柯, 张艳, 李浩. 移动传感器网络保持网络连通性控制[J]. 电子测量与仪器学报, 2016, 30(11): 1657-1663. LOU K, ZHANG Y, LI H. Connectivity preservation control of mobile sensor network[J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(11): 1657-1663. (in Chinese) |
| [9] |
娄柯, 崔宝同, 李纹. 基于蜂拥控制的移动传感器网络目标跟踪算法[J]. 控制与决策, 2013, 28(11): 1637-1642, 1649. LOU K, CUI B T, LI W. Target tracking algorithm of mobile sensor networks based on flocking control[J]. Control and Decision, 2013, 28(11): 1637-1642, 1649. (in Chinese) |
| [10] |
AGARWAL P, DESHPANDE A D. Subject-specific as-sist-as-needed controllers for a hand exoskeleton for re-habilitation[J]. IEEE Robotics and Automation Letters, 2018, 3(1): 508-515. DOI:10.1109/LRA.2017.2768124 |
| [11] |
OLFATI-SABER R. Flocking for multi-agent dynamic systems:algorithms and theory[J]. IEEE Transactions on Automatic Control, 2006, 51(3): 401-420. DOI:10.1109/TAC.2005.864190 |








