管道被称为化工生产的脉络,它将石油化工装置中的设备连接起来,完成各道工序。然而随着生产工艺过程的日益复杂、处理量的加大,往往会引起管道及设备的振动[1]。强烈的振动会使管道的连接部位发生破裂或松动,导致介质泄漏甚至引发爆炸,造成严重事故。
在工程实际中,通常采用增加孔板、设置缓冲罐或滤波器、增设管架等措施来控制管道振动[2],但这些方法均需在设备停车的情况下实施,影响其正常生产,并且还可能会使管道产生附加应力。增加孔板可以消除管道中的气流脉动,但孔板的安装需要在设备停车的情况下进行[3];缓冲罐通常被用于压缩机上,可以显著改善管道中的流量和压力脉动现象[4],然而其效果易受到现场空间结构的限制[5];增加管架是针对低频振动管道常用的方法,但是管架不能从根本上解决振动,而是会将振动传递到其他地方[6],引起二次应力。
山东某化工厂分馏装置的换热器出口至初馏塔入口管线自投产以来就一直存在振动过大问题,虽然已采取了一些措施,例如将管道弯头转弯半径扩大,但仍然存在肉眼可见的晃动。本文将阻尼减振技术应用到管道振动问题上,该技术不仅对抑制管道振动非常有效,还可以在设备不停车的条件下实施,且不会产生附加应力。
1 管道参数及振动情况此次改造的管线为分馏装置的E1001B换热器壳程出口至初馏塔入口的管线,该换热器壳程介质为中质原油,设计流量416 t/h,实际工作时流量为370 t/h,压力0.9 MPa,温度220 ℃,换热器出口管径为DN400,换热器出口管线现场分布如图 1所示。

|
图 1 换热器出口管线现场分布图 Fig.1 View of the heat exchanger outlet pipeline |
从图 1中可以发现,该换热器出口至初馏塔入口管线跨度较长,存在多个弯头,且管道支撑较少,有很长一段的悬臂管线,管道刚度较低。改造前,该管线存在明显的肉眼可见的晃动。
用德国SCHENCK公司生产的Smart Balancer振动测试系统对管道振动进行测量,测量结果显示,各个测点振动幅值均超过1 000 μm,最大达到2 089 μm。由于换热器出口管道内介质温度极高且易燃易爆,对工作人员的生命安全造成严重威胁,因此急需进行减振改造,消除安全隐患。
2 振动原因分析 2.1 管道振动原因(1) 所研究管线走向复杂,经过6个弯头,管道中的原油在流经这些弯头处时流速和流向会发生急剧变化,对管道产生巨大冲击力[7];管道中原油含水量大,在220 ℃下,水分蒸发随介质进入管道,出现气液两相,造成压力波动,从而产生激振力,对管壁造成冲击。
(2) 换热器出口至初馏塔入口管线长度超过20 m,主要靠两个弹簧支架支撑,管道缺少支撑,整体刚度较小;另外管道中介质为液体且流量大,导致弹簧支架受力过大从而失效,管道在流体冲击下易造成振动。
(3) 整条管线位于24 m高的新起平台上,平台本身支撑立柱单薄,而且顶部受力较大,容易引起晃动。
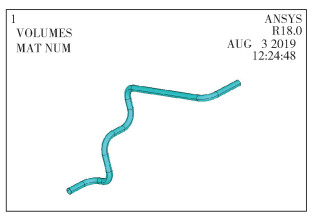
2.2 管道模态分析在ANSYS 16.0有限元分析软件中依照现场实际测量尺寸对管道结构进行有限元建模,如图 2所示。采用Solid 185实体单元,设定其泊松比为0.3,弹性模量为2.1×1011 Pa,对模型定义属性,划分网格,施加约束后进行分析。经过计算,换热器出口管道前5阶固有频率如表 1所示。
|
图 2 管线模型 Fig.2 Pipeline model |
| 下载CSV 表 1 换热器出口管道前5阶固有频率 Table 1 Fifth order natural frequency of the heat exchanger outlet pipe |
在工程上,激振频率的共振区为0.8f~1.2f(f代表激振频率),当管道的固有频率刚好落在共振区内时,就会导致管道强烈振动,并且越接近激振频率就越容易产生共振[8]。现场实测换热器出口管道的振动频率为5 Hz,处于二阶固有频率共振区(3.65~5.47 Hz)内,分析可知,高温原油的剧烈脉动引起了换热器出口管线的基频振动[9],是导致换热器出口管道发生共振的主要原因。
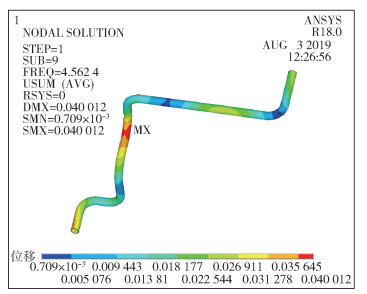
换热器出口管道第2阶模态下的振型图如图 3所示。
|
图 3 管道第2阶模态下位移云图 Fig.3 Mode shape of the second-order mode of the pipeline |
从图 3中可以看到管道在两个弯头位置振动最大,管道模拟的振动情况与现场实际情况相符。
2.3 管内流体脉动的CFD模拟在换热器出口至初馏塔入口管道中,流体经过6个弯头,运动状态不断发生改变,形成压力脉动,使管道产生强烈振动。将SolidWorks中建立的模型导入Fluent中进行流场分析[10],根据实际参数,设置模型为湍流模型,管道入口速度(velocity-inlet)为0.787 7 m/s,水力直径(hydraulic diameter)为0.406 m,出口压力(pressure-outlet)为0.9 MPa,其余边界条件设置为固体壁面(wall)。将Fluent中流体计算结果作为载荷施加到workbench中的管道结构上,得到管道中的速度流线图如图 4和图 5所示。
|
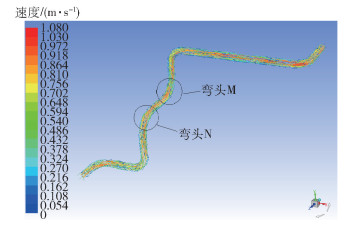
图 4 流体CFD仿真速度流线图 Fig.4 Velocity streamline diagram in the CFD simulation of the fluid |

|
图 5 弯头M和N处流线放大图 Fig.5 Enlarged flow line at elbows M and N |
以弯头M和N为例,如图 5所示,由于流体经过弯头时,弯头内外侧的曲率半径不同,使流体在弯头两侧的离心力不同[11],进而形成压差,在弯头位置出现流体流动旋涡,最终产生流体脉动[12-13],对管道产生激振力,导致管道振动。
3 阻尼减振模拟分析 3.1 管道阻尼减振技术黏滞型管道阻尼器广泛应用于化工厂与工业设备的各种管道系统和其他装置上,其主要由上连接件、下连接件、阻尼缸、动体和密封片组成。阻尼缸中装有黏滞性阻尼液,动体浸没在阻尼液中。上连接件与振动管道相连,可以将管道振动的能量传递至动体,使得动体搅动阻尼液,从而产生黏滞阻尼力。阻尼液是由特定的高黏度液体制成,可以将管道系统的振动能量以热能的形式释放到大气中,从而控制管道系统的振动[14]。
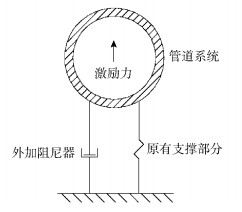
在管道上施加阻尼器后,可以将管道系统简化为如图 6所示的模型,管道相当于一个质量块,受到外部激励力、支撑结构的弹性力和阻尼器中的阻尼力作用[15]。
|
图 6 管道振动模型 Fig.6 Pipe vibration model |
选取管道的主振方向进行分析,则管道振动的微分方程为
| $ m \ddot{x}+c \dot{x}+k x=F \cos \omega t $ | (1) |
式中,m为系统质量,c为阻尼系数,k为系统刚度,x为管道振幅,F为激励力,ω为振动频率,t为时间。
由式(1)可知,在系统中施加了阻尼后,对耗散振动系统的能量会产生一定效果。
管道上某点的强迫振动稳态响应为
| $ x=B \sin (\omega t-\varphi) $ | (2) |
将式(2)对时间求导得到阻尼力大小为
| $ F_{\mathrm{d}}=c \dot{x} $ | (3) |
在整个周期内对阻尼力积分得到阻尼器在一个周期内耗散的能量为
| $ W_{e}=c \pi \omega B^{2} $ | (4) |
式中,B为管道振幅;φ为振动相位;Fd为黏滞阻尼力大小;Wc为黏滞阻尼力在一个振动周期内做的功。
由式(4)可知,在管道振动最大的位置加装阻尼器,阻尼器耗散的能量最多,减振效果最好。
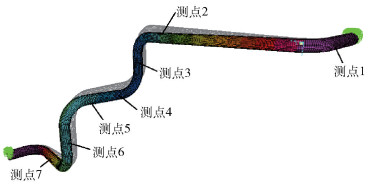
3.2 阻尼减振模拟计算根据换热器出口管道的具体参数,利用SAP2000建立管道模型,节点数共14 376个,设置网格边长50 mm,材料选择Q235。划分网格后,在外界激振力作用处施加时程载荷,具体如下:在每个弯头处选择680个节点施加载荷,选择sine函数作为载荷时程函数,函数周期设置为0.2 s。每个节点处施加大小为5 N的力,即每个弯头处存在3 400 N的作用力,模拟管道内流体冲击力。得到管道无阻尼振型图如图 7所示。为便于下文对比,在模型中标记了7个测点,具体位置如图 7所示。
|
图 7 管道无阻尼振型图 Fig.7 Undamped vibration mode of the pipeline |
从图 7中可以看出,未加阻尼器时,管道在流体的冲击作用下,弯头处刚度最差,变形也最大,这与现场的实际情况吻合。
为确定此次改造中阻尼器的选型和安装数量,分别模拟计算了不同阻尼系数和不同安装数量下的管道振动位移值。
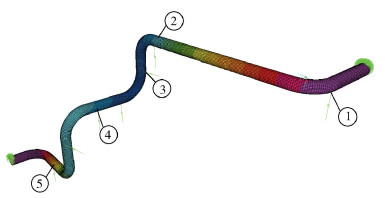
3.2.1 不同阻尼系数为对比不同阻尼系数阻尼器的减振效果,分别对实验室现有的3种阻尼器A、B、C进行阻尼减振模拟计算,3种阻尼器A、B、C的阻尼系数分别为76、105、137 (kN ·s)/m。模拟时首先在振动最大的5个弯头处各安装1个阻尼器,图 8为安装阻尼器A后的管道振型图。提取测点1~测点7的振动幅值进行对比,如表 2所示。
|
图 8 安装阻尼器A后的管道振型图 Fig.8 Modal diagram of the pipeline after applying damper A |
| 下载CSV 表 2 各测点在安装3种阻尼器前后的振动幅值 Table 2 Vibration values at each measuring point before and after applying three kinds of dampers |
从表 2中可以看出,随着3种阻尼器阻尼系数的增大,各测点的振动幅值逐渐减小,减振效果越来越明显,因此确定选择阻尼系数为137 (kN ·s)/m的阻尼器C。这是由于黏滞阻尼器的减振效果是由其所产生的阻尼力F=CVα决定的,其中C为阻尼器的阻尼系数,V为振动速度,α为阻尼指数,通常取0.3。相同条件下,黏滞阻尼器所产生阻尼力的大小与阻尼系数成正比。
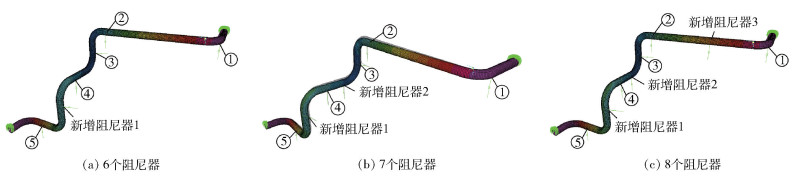
3.2.2 不同安装数量在3.2.1节已经安装5个阻尼器C的基础上,继续增加阻尼器数量分别至6、7、8个,分别计算3种方案下管道的振动位移值,计算结果如图 9所示。同样读取测点1~测点7(测点位置如图 7)的振动数据,如表 3所示。
|
图 9 安装不同数量阻尼器后的管道振型图 Fig.9 Modal diagram of the pipeline after applying different numbers of dampers |
| 下载CSV 表 3 安装不同数量阻尼器后的振动幅值 Table 3 Vibration values after applying different numbers of dampers |
从表 3可知,在管道上施加阻尼器数量越多,测点振动幅值越小,但相对于施加7个阻尼器而言,施加8个后的测点振动幅值下降很小,有的测点振动幅值甚至不变。由于管道在新增阻尼器3的位置安装阻尼器条件苛刻,成本较高,综合考虑,决定采用图 9(b)的方案,安装7个阻尼器。
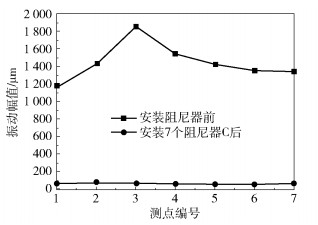
综上,最终的方案为在图 9(b)所示的位置安装7个阻尼器C,其参数如下:刚度137 000 N/mm,阻尼指数0.3,阻尼系数137 (kN ·s)/m,阻尼器各个方向最大位移量为20 mm。将管道在各测点的原始振动幅值和安装7个阻尼器C后的振动幅值绘制成折线图,如图 10所示。
|
图 10 安装阻尼器前后振动幅值对比 Fig.10 Comparison of the vibration values before and after setting a damper |
由图 10可知,与安装阻尼器前相比,安装阻尼器后管道的振动幅值均大幅降低,说明管道在弯头处的振动得到有效控制。
4 减振方案实施及减振效果根据阻尼减振模拟仿真以及有限元分析结果,并考虑到现场安装条件和厂方成本要求,本次改造依照模拟得出的最优方案,在管道相应位置处安装了7个黏滞型阻尼器,使设备在安全范围内运行,现场阻尼器安装实物图如图 11所示。

|
图 11 阻尼器安装实物图 Fig.11 View of the damper installation |
安装阻尼器前后,分别使用Smart Balancer振动测试系统对管道上测点1~测点7(同图 7中各测点位置)进行振动测量,安装阻尼器前后各测点振动数据如表 4所示。
| 下载CSV 表 4 安装阻尼器前后各测点振动位移 Table 4 Vibration displacement at measuring points before and after installation of dampers |
从表 4可以看出,减振改造前,在换热器出口管道各测点振动很大,改造后振动最大的测点3振动位移由2 089 μm降至50 μm,降幅最大达到97.6%,其他测点的振动降幅也均达到90%以上,表明管道振动得到明显的抑制。
5 结论(1) 通过对换热器出口至初馏塔入口管线振动机理进行分析,发现引起管道振动的主要原因有两个:①内部流体的激振力频率与管道第2阶固有频率相近;②管道内部流体存在明显的压力脉动,对管道造成强烈的激振力。
(2) 运用有限元软件对振动管线进行阻尼减振模拟仿真,确定了阻尼器的选型和安装数量,优化了安装方案,最后在不停机的情况下,在管道上安装了7个黏滞型阻尼器后,管线的振动位移平均降低了90%,保证了分馏装置的安全运行。
(3) 在化工厂的管线振动问题中引入阻尼减振技术,可以有效地吸收管线的振动能量,且不会引起临近管线的振动。
| [1] |
黄振仁, 魏新利. 过程装备成套技术[M]. 2版. 北京: 化学工业出版社, 2008. HUANG Z R, WEI X L. Complete technology of process equipment[M]. 2nd ed. Beijing: Chemical Industry Press, 2008. (in Chinese) |
| [2] |
袁伟, 赵杰, 邓贵德, 等. 孔板及缓冲罐对管内气流脉动影响实验研究[J]. 中国特种设备安全, 2018, 34(7): 15-18. YUAN W, ZHAO J, DENG G D, et al. Experimental study on the effect of orifice plate and buffer tanks on airflow pulsation in pressure piping[J]. Safety of Special Equipment in China, 2018, 34(7): 15-18. (in Chinese) DOI:10.3969/j.issn.1673-257X.2018.07.004 |
| [3] |
白文杰, 李涌泉, 谢旭梦, 等. 孔板消减气流脉动的数值模拟[J]. 应用力学学报, 2013, 30(6): 828-832. BAI W J, LI Y Q, XIE X M, et al. Numerical simulation of reducing air flow pulsation with orifice plate[J]. Chinese Journal of Applied Mechanics, 2013, 30(6): 828-832. (in Chinese) |
| [4] |
叶少宁, 李颖, 王俊东. 缓冲罐在往复泵长距离输送管道减振中的应用[J]. 新疆石油天然气, 2009, 5(2): 77-81. YE S N, LI Y, WANG J D. Application of buffer tank in vibration reduction of long distance pipeline of reciprocating pump[J]. Xinjiang Oil & Gas, 2009, 5(2): 77-81. (in Chinese) DOI:10.3969/j.issn.1673-2677.2009.02.019 |
| [5] |
郭景宏.往复压缩机管系振动机理分析及实验研究[D].兰州: 天华化工机械及自动化研究设计院有限公司, 2014: 9-15. GUO J H. Piping vibration mechanism analysis and experimental study for reciprocating compressor[D]. Lanzhou: Tianhua Institute of Chemical Machinery and Automation Co., Ltd., 2014: 9-15. (in Chinese) |
| [6] |
SOROKIN S V, OLHOFF N, ERSHOVA O A. Analysis of the energy transmission in spatial piping systems with heavy internal fluid loading[J]. Journal of Sound and Vibration, 2008, 310(4): 1141-1166. |
| [7] |
陈章华. 压缩机出口管道振动原因分析及对策[J]. 化工设备与管道, 2016, 53(2): 51-53. CHEN Z H. Cause analysis and countermeasure of vibration of compressor outlet pipeline[J]. Process Equipment and Piping, 2016, 53(2): 51-53. (in Chinese) DOI:10.3969/j.issn.1009-3281.2016.02.013 |
| [8] |
冯浩然, 何立东, 胡航领. 低温甲醇洗工艺管线振动分析及阻尼减振研究[J]. 北京化工大学学报(自然科学版), 2017, 44(5): 80-84. FENG H R, HE L D, HU H L. Vibration analysis and damping vibration reduction for a rectisol process pipeline[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2017, 44(5): 80-84. (in Chinese) |
| [9] |
崔巍升, 宫建国, 金涛. 化工厂管道振动原因分析及控制[J]. 流体机械, 2011, 39(10): 34-38. CUI W S, GONG J G, JIN T. Analysis and controlling of pipeline vibration in chemical plant[J]. Fluid Machinery, 2011, 39(10): 34-38. (in Chinese) DOI:10.3969/j.issn.1005-0329.2011.10.008 |
| [10] |
宋学官, 蔡林, 张华. ANSYS流固耦合分析与工程实例[M]. 北京: 中国水利水电出版社, 2012. SONG X G, CAI L, ZHANG H. ANSYS fluid structure coupling analysis and engineering example[M]. Beijing: China Water & Power Press, 2012. (in Chinese) |
| [11] |
柯兵. 管路弯头流致振动的影响因素分析[J]. 中国舰船研究, 2018, 13(2): 70-75. KE B. Influence factors analysis of flow-induced vibration of elbow inpiping system[J]. Chinese Journal of Ship Research, 2018, 13(2): 70-75. (in Chinese) DOI:10.3969/j.issn.1673-3185.2018.02.009 |
| [12] |
党锡淇, 陈守五. 活塞式压缩机气流脉动与管道振动[M]. 西安: 西安交通大学出版社, 1984. DANG X Q, CHEN S W. Air flow pulsation and pipeline vibration of piston compressor[M]. Xi'an: Xi'an Jiaotong University Press, 1984. (in Chinese) |
| [13] |
付永领, 荆慧强. 弯管转角对液压管道振动特性影响分析[J]. 振动与冲击, 2013, 32(13): 165-169. FU Y L, JING H Q. Elbow angle effect on hydraulic pipeline vibration characteristics[J]. Journal of Vibration and Shock, 2013, 32(13): 165-169. (in Chinese) DOI:10.3969/j.issn.1000-3835.2013.13.031 |
| [14] |
吕峰. 粘滞阻尼器在框架结构减震设计中的运用[J]. 居舍, 2018(15): 88-89. LV F. Application of viscous dampers in seismic design of frame structures[J]. Residence, 2018(15): 88-89. (in Chinese) |
| [15] |
张俎琛, 何立东, 万方腾, 等. 离心压缩机管线过滤分离装置阻尼减振技术[J]. 石油机械, 2018, 46(11): 128-133. ZHANG Z C, HE L D, WAN F T, et al. Damping technology for filter and separation device of centrifugal compressor pipeline[J]. China Petroleum Machinery, 2018, 46(11): 128-133. (in Chinese) |








