2. 中国石油天然气股份有限公司 石油化工研究院 大庆化工研究中心, 大庆 163714;
3. 北京化工大学 机电工程学院, 北京 100029
2. Daqing Chemical Research Center, Petrochemical Research Institute, China National Petroleum Corporation, Daqing 163714;
3. College of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing 100029, China
液滴撞击固体表面的现象在过程工业中较为常见,如横管降膜蒸发[1]、喷淋吸收[2]和涡轮机的冷却[3]等。在以传质为主要目的的过程中,液滴撞击固体表面过程中的表面积变化对传质性能有很大的影响。Ai等[4]在对高速分散反应器的气体吸收性能进行的研究中,建立了用于预测反应器传质特性的传质表面积模型;在该模型中,液滴与反应器固体表面的碰撞是一个增大传质面积的重要过程。研究物性和操作条件对液滴撞击固体表面过程中表面积变化的影响,进而深入理解此过程,可为此类设备的设计提供指导。
关于液滴撞击固体表面过程研究的方法主要有实验、理论分析和数值模拟。文献[5]~[9]通过定量实验研究了液滴撞击静止的固体表面时铺展直径随时间变化的影响因素,如液滴的撞击速度、液体的流变性质和表面张力、固体表面的粗糙度等,发现撞击速度的增加、黏度的减小、表面张力的减小、表面粗糙度的减小均会增大最大铺展直径,并提出了一系列最大铺展直径的经验关联式。而当固体表面处于运动状态时,在液滴撞击过程中则通常可以观察到不对称的铺展甚至飞溅[10]。通过实验研究可以得到液滴撞击后的不同形态、液滴物性和撞击速度对铺展直径的影响,以及可预测液滴最大铺展直径的经验关联式,有助于加深对液滴撞击过程的理解。
针对液滴撞击固体表面过程的理论分析以能量法最为常见,其主要原理是基于液滴撞击过程中表面能、动能、黏性耗散三者的总能量守恒。利用此方法可得到液滴的无量纲最大铺展直径关于液滴的韦伯数、雷诺数和静态接触角的表达式,但因针对液滴内黏性耗散的假设不同,所得到的表达式有所差异[11-12]。数值模拟是研究液滴撞击固体表面现象的重要手段,通过数值模拟除了可以得到液滴铺展直径、铺展高度和铺展速度等宏观信息外,还能了解液滴内部的流场信息,有助于更为深入地理解液滴撞击过程中铺展的机理[13-15]。
目前文献中关于各类因素对液滴铺展线速度和铺展面积的影响,以及撞击过程中液滴的表面能、动能和黏性耗散的变化的研究较少,因此本文采用实验的方法研究了液滴的物性和操作条件对其撞击固体表面过程中的铺展直径、铺展速度和铺展面积的影响,并结合能量法对表面能、动能和黏性耗散在撞击过程中的变化进行分析,以揭示液滴撞击固体表面过程的特点。
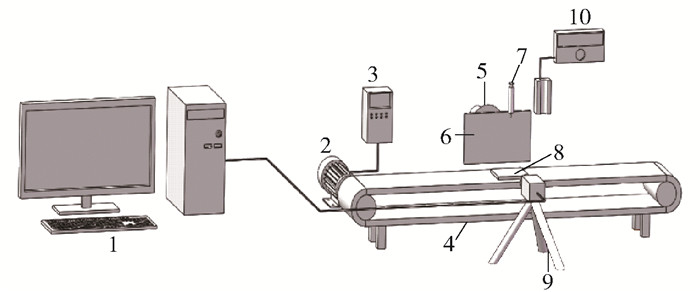
1 实验装置和方法实验系统示意图如图 1所示。通过注射泵驱动液体在注射器的针尖处产生液滴,液滴直径和速度可分别通过针头内径和针头高度进行控制和调节。电脑与高速相机连接,并控制其以486帧/s的频率记录液滴撞击不锈钢板表面的过程(分辨率320pixel×256pixel),实验中图像的物理分辨率为0.024mm/pixel。传送带的平动速度通过调节变频器改变电机的转速实现。
|
1—电脑;2—电机;3—变频器;4—传送带;5—光源;6—散光板;7—注射器;8—不锈钢板;9—高速相机;10—注射泵。 图 1 实验系统示意图 Fig.1 Schematic diagram of the experimental system |
实验所用物质的物性参数和实验条件如表 1、2所示,其中US为平面的运动速度,UD为液滴的撞击速度。
| 下载CSV 表 1 物质的物性参数 Table 1 Physical parameters of materials |
| 下载CSV 表 2 操作条件参数 Table 2 Operating parameters |
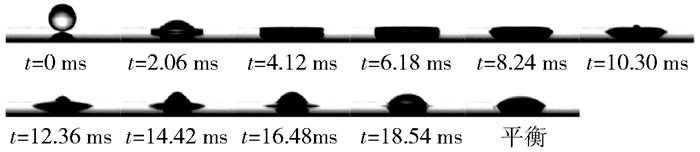
图 2是一个质量分数20%的甘油水溶液液滴撞击静止固体表面的典型过程。液滴(D0=2.85mm)以0.97m/s的速度撞击在不锈钢表面上(t=0ms),经过铺展达到最大铺展面积(t=2.06ms),随后经历回缩、再铺展以及震荡的过程(t=4.12 ~ 18.54ms),直至达到平衡。
|
图 2 甘油质量分数20%的液滴撞击静止的不锈钢表面(UD=0.97m/s) Fig.2 Droplets with 20% glycerol mass fraction impacting on the stationary stainless steel surface (UD=0.97m/s) |
液滴的宏观信息如体积、铺展直径、铺展速度等可以通过图像识别获取。本文使用Matlab对高速相机记录的液滴照片进行去噪、去除杂点、中值滤波、二值化等步骤的处理,再从所得到的二值化图片中获取上述参数。其中,液滴的铺展速度可由液滴铺展线在相邻两张照片的坐标差与拍摄频率相乘得到。由于液滴在撞击过程中的形态始终保持轴对称,可以使用旋转积分的方法求得液滴的体积[11]。
|
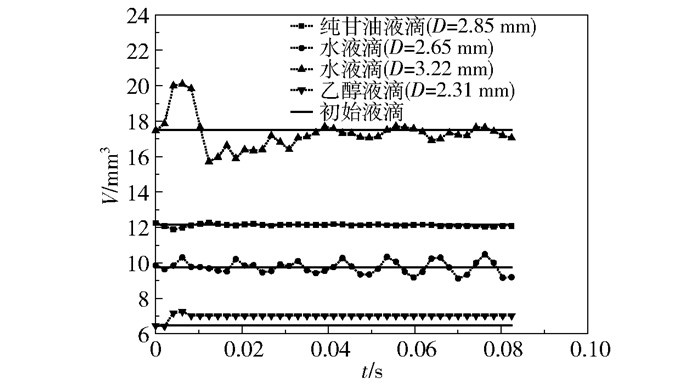
图 3 不同物性和直径的液滴在撞击过程中的体积 Fig.3 Volume of droplets with different physical properties and diameters during impact |
图 3所示为使用图像处理的方法得到的4个不同物性和直径的液滴在撞击过程中体积随时间的变化。从图中可以看到,直径为2.65mm的水液滴、直径为3.22mm的水液滴、直径为2.85mm的纯甘油液滴、直径为2.31mm的乙醇液滴计算所得体积与初始体积的最大误差分别为7.7%、14%、2.2%、12%,说明本文采用的图像处理和分析方法可对液滴撞击固体表面的过程进行较为准确的定量分析。
2 结果与分析 2.1 铺展因子和铺展速度 2.1.1 铺展因子若一个具有初始球形当量直径D0以及初始面积S0的液滴在撞击过程中经过铺展时间t后的铺展直径为D,铺展面积为S,且此时铺展线速度为U,则定义相应的无量纲铺展因子D*、无量纲铺展速度U*、无量纲铺展面积S*和无量纲铺展时间t*分别为
| $ D^{*}=\frac{D}{D_{0}} $ | (1) |
| $ U^{*}=\frac{U}{U_{\mathrm{D}}} $ | (2) |
| $ S^{*}=\frac{S}{S_{0}} $ | (3) |
| $ t^{*}=\frac{t U_{\mathrm{D}}}{D_{0}} $ | (4) |
此外,液滴的撞击雷诺数Re、韦伯数We和切向韦伯数Wet分别为
| $ R e=\frac{\rho D_{0} U_{\mathrm{D}}}{\mu} $ | (5) |
| $ W e=\frac{\rho D_{0} U_{\mathrm{D}}^{2}}{\sigma} $ | (6) |
| $ W e_{\mathrm{t}}=\frac{\rho D_{0} U_{\mathrm{S}}^{2}}{\sigma} $ | (7) |
若固体表面静止,则切向韦伯数为零。
具有一定初始动能的液滴在撞击表面后向外铺展,与此同时液滴的黏性力和表面张力阻碍铺展。液滴到达最大铺展之后开始回缩,此时表面张力则是回缩的驱动力,而黏性力是回缩的阻力。
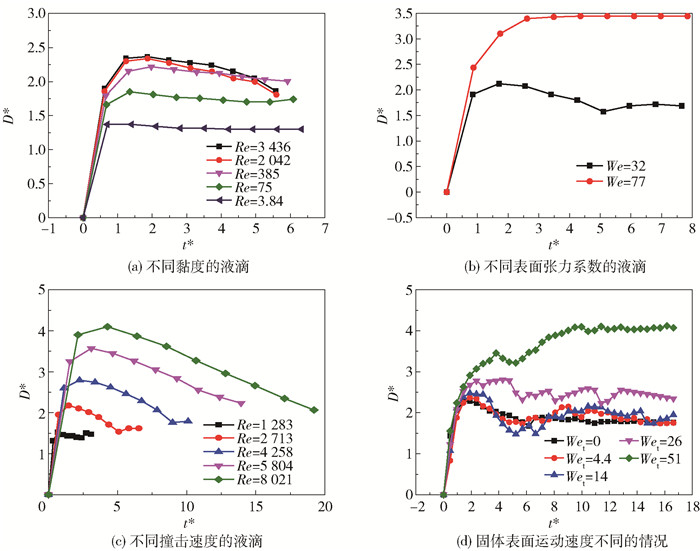
如图 4(a)所示,黏度较大的液滴受到的黏性力较大,其铺展直径和最大铺展直径均较小,不发生回缩现象。如图 4(b)所示,具有较小表面张力的乙醇液滴在铺展过程中受到的阻力较小,其达到最大铺展直径的时间较长,最大铺展直径较大。然而,由于较小的表面张力难以克服黏性力,导致无法产生回缩。
|
图 4 不同物性和操作条件下铺展因子的变化 Fig.4 Variation in spreading factors for different physical properties and operating conditions |
如图 4(c)所示,具有较大初始动能的液滴克服黏性力和表面张力之后的剩余能量更多,铺展直径和铺展时间均得以增加。当固体表面处于运动状态时,液滴的铺展直径为液滴沿固体表面运动方向的铺展长度。图 4(d)的结果表明,随着固体表面运动速度的增大,液滴的最大铺展直径和达到最大铺展直径的时间增加,这是固体表面给液滴施加的额外能量造成的。
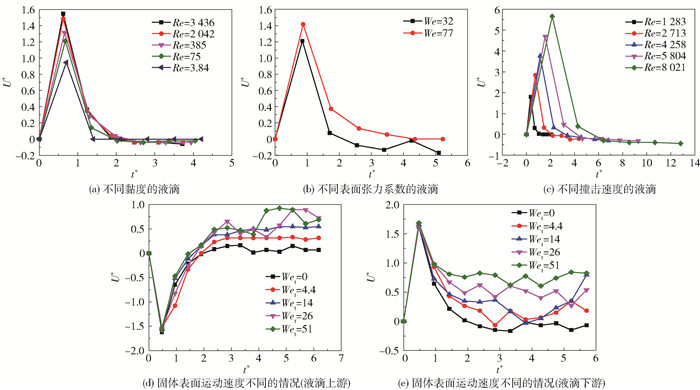
2.1.2 铺展速度图 5所示为具有不同物性和撞击速度的液滴的U*随t*的变化。液滴撞击静止固体表面时,铺展速度在撞击后短时间内达到最大值,然后在黏性力和表面张力的作用下,铺展速度减小至0,并达到最大铺展;随后液滴开始回缩,但速度远小于初始铺展速度。在图 5(a)中,黏度较大的液滴在铺展和回缩过程中受到的阻力较大,铺展和回缩速度均较小。如图 5(b)所示,表面张力较大的液滴在铺展时受到的阻力较大,在回缩时动力较大,此时产生较小的铺展速度和较大的回缩速度。如图 5(c)所示,撞击速度较大的液滴具有较大的初始动能,克服黏性力和表面张力之后的剩余能量较大,在铺展和回缩时均具有较大的速度。
|
图 5 不同物性和操作条件下无量纲铺展线速度的变化 Fig.5 Variation of dimensionless spreading line speed for different physical properties and operating conditions |
在固体表面水平运动时,定义液滴上游方向为液滴铺展与固体表面运动相同的方向,反之为液滴下游方向。如图 5(d)所示,液滴上游铺展线速度(绝对值)在撞击后的短时间内增加到最大值,但由于其方向与固体表面运动方向相反,随着固体表面运动速度的增大,液滴受到的黏性力增大,且上游铺展线速度降低。液滴上游铺展线速度降至0之后,黏性力与上游铺展线速度的方向开始相同,此时黏性力作正功,因此固体表面运动速度的增大会使得上游铺展线速度增大,直至上游铺展线速度与表面运动速度相等。如图 5(e)所示,在撞击的瞬间,液滴下游铺展线速度大于表面的运动速度,此时黏性力做负功,且下游铺展线速度会逐渐减小至固体表面运动速度。
2.1.3 最大铺展直径最大铺展直径Dmax是液滴撞击固体表面过程中的重要参数,定义相应的液滴最大无量纲铺展因子如式(8)所示
| $ D_{\max }^{*}=\frac{D_{\max }}{D_{0}} $ | (8) |
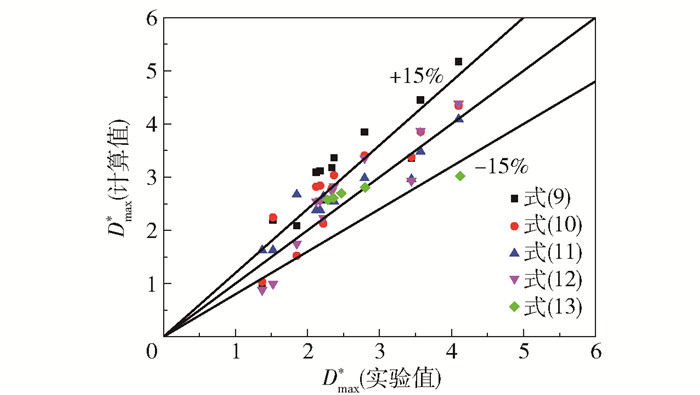
表 3为文献中几个关于液滴最大无量纲铺展因子的关联式。将这些文献中的Dmax*计算值与本文实验中的结果进行对比,结果如图 6所示。文献[16]中的液滴撞击在玻璃表面上,而在本文实验中液滴撞击在不锈钢固体表面上,由于玻璃表面的润湿性较好,液滴撞击在其上的铺展直径较大,因此使用由实验结果拟合而得的式(9)[16]计算的Dmax*大于本文实验值,平均误差约为20%。由于文献[12]在计算黏性耗散时仅考虑了边界层内的黏性耗散,使得其计算值较小,而本文采用能量法时认为有更多的能量转化为了表面能,计算所得的Dmax*大于实验值,平均误差约为20%。在3 < Re < 9000,27 < We < 300时,由式(11)[17]计算所得的Dmax*与实验值的平均误差约为15%。当75 < Re < 9000,27 < We < 300时,由式(12)[18]计算所得的Dmax*与实验值的平均误差约为15%。在0 < We < 40,0 < Wet < 51时,由式(13)[19]计算所得的液滴撞击运动固体表面的Dmax*与实验值的误差小于15%。
| 下载CSV 表 3 最大无量纲铺展因子的不同模型 Table 3 Different models of the largest dimensionless spreading factor |
|
图 6 文献中Dmax*计算值与本文实验值对比 Fig.6 Comparison of Dmax* calculated values in the literature with our experimental value |
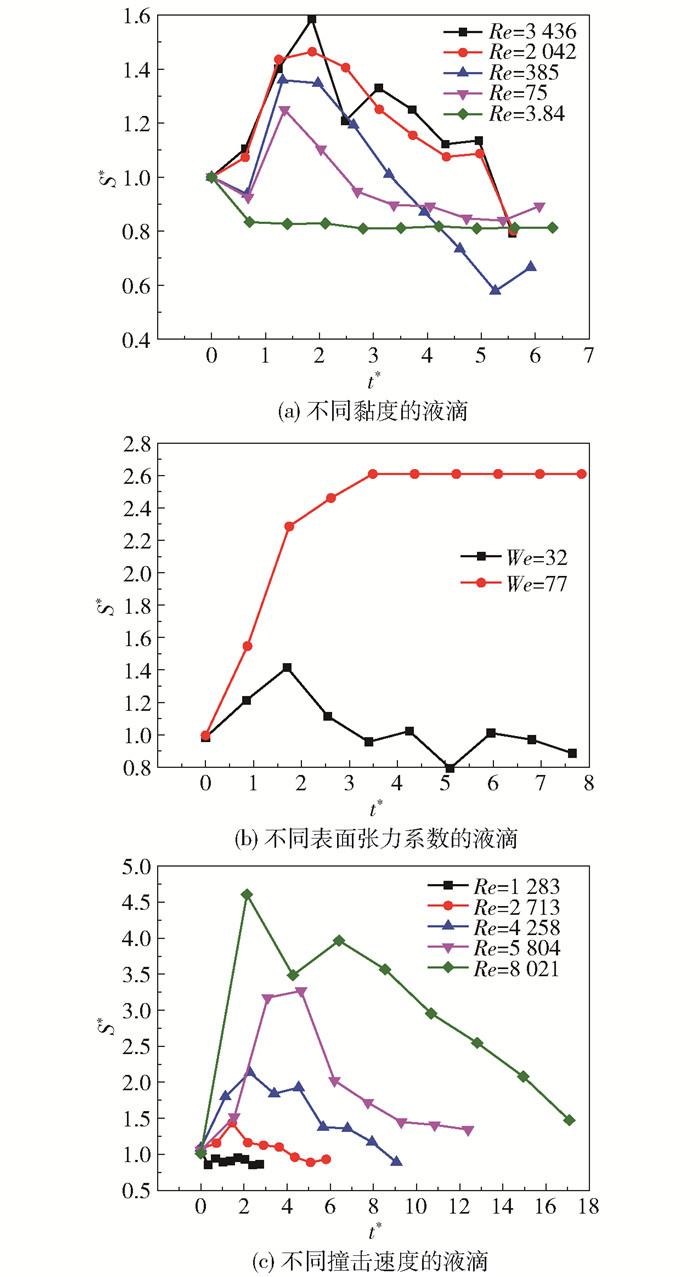
不同物性和操作条件下无量纲铺展面积的变化如图 7所示。可以看出,铺展面积随时间变化的一般趋势为先增大后减小。随着黏度的增大,或表面张力的增大,或撞击速度的减小,液滴的铺展面积和最大铺展面积均减小。当液滴黏度过大或撞击速度过小时,其铺展面积始终小于液滴的初始表面积;而当液滴表面张力系数较小或撞击速度较大时,其最终铺展面积大于液滴的初始表面积。
|
图 7 不同物性和操作条件下无量纲铺展面积的变化 Fig.7 Changes in dimensionless spreading area for different physical properties and operating conditions |
假设液滴撞击固体表面后达到最大铺展时近似形成圆柱状,根据式(14)可计算液滴的Smax*
| $ S_{\max }^{*}=\frac{1}{4} D_{\max }^{* 2}+\frac{2}{3} \frac{1}{D_{\max }^{*}} $ | (14) |
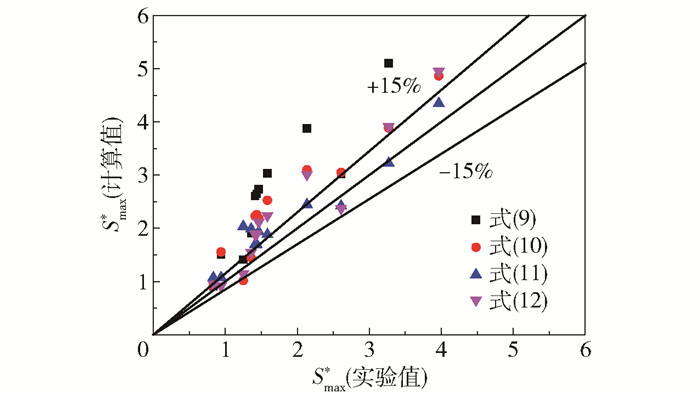
图 8为文献中Smax*计算值与本文实验值对比。将式(9)~(12)代入式(14)求得的Smax*与实验值的平均误差分别约为30%、30%、20%和20%。这是由于液滴至最大铺展时的形状并不是严格的圆柱,其实际铺展面积小于相应的圆柱,则将液滴至最大铺展时的Smax*形状认为是圆柱形并根据式(14)计算得到的值大于实验值。
|
图 8 文献中Smax*计算值与本文实验值对比 Fig.8 Comparison of Smax* calculated values in the literature with our experimental value |
对Smax*的实验值进行拟合,得到Smax*关于Re和We的关系式如式(15)所示
| $ S_{\max }^{*}=0.203 R e^{0.064} W e^{0.43} $ | (15) |
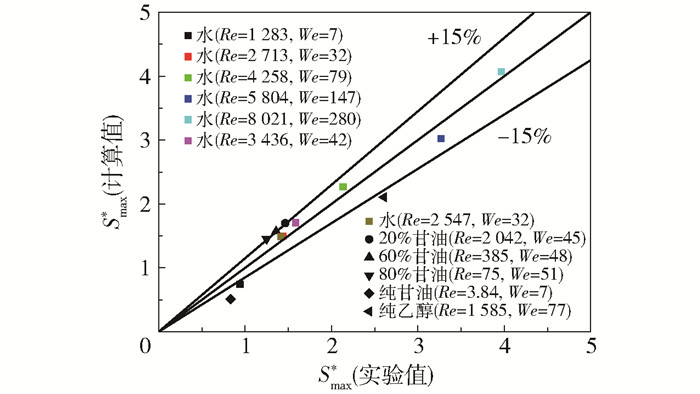
图 9为Smax*实验值与式(15)的Smax*计算值的对比,式(15)的Smax*计算值与实验值误差在大部分情况下都小于15%,因此在75 < Re < 9000,7 < We < 300时,可使用式(15)预测液滴撞击不锈钢固体表面的最大铺展面积。
|
图 9 实验值与式(15)Smax*计算值的对比 Fig.9 Comparison of the experimental values of Smax* with the calculated value using Smax* of equation (15) |
液滴撞击固体表面的过程中,若忽略势能的变化,能量在动能、表面能、黏性耗散三者之间转换。设液滴的初始表面能为ES0,初始动能为EK0,液滴在撞击后任意瞬间的表面能为ES,动能为EK,黏性耗散为EV。此时,有关系式
| $ E_{\mathrm{S} 0}+E_{\mathrm{K} 0}=E_{\mathrm{S}}+E_{\mathrm{K}}+E_{\mathrm{V}} $ | (16) |
式中,
| $ {E_{{\rm{S0}}}} = {\sigma _{1{\rm{g}}}}{\rm{ \mathit{ π} }}D_0^2 $ | (17) |
| $ E_{\mathrm{K} 0}=\frac{1}{2} \rho\left(\frac{1}{6} \pi D_{0}^{3}\right) U_{\mathrm{D}}^{2} $ | (18) |
液滴的表面能包括液气表面能和液固表面能,其计算式如式(19)所示。
| $ E_{\mathrm{S}}=\sigma_{1 \mathrm{g}} S+\frac{1}{4} \sigma_{\mathrm{sl}} \pi D^{2} $ | (19) |
式中σ1g和σs1分别为液滴的液气表面张力系数和液固表面张力系数。σs1的计算式如式(20)所示。
| $ \sigma_{\mathrm{sl}}=\frac{\sigma_{\mathrm{lg}}}{2}\left(\sqrt{1+(\sin \theta)^{2}}-\cos \theta\right) $ | (20) |
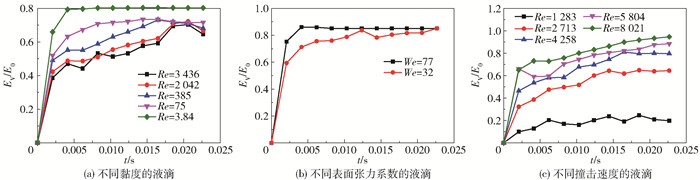
图 10为不同物性和操作条件下液滴表面能的变化。由图 4(a)、图 7(a)和式(19)均可得到液滴铺展直径和铺展面积随时间先增大后减小的一般规律,且随着黏度的增加,液滴的铺展直径和铺展面积均减小,液滴表面能增加的速率也在降低。
|
图 10 不同物性和操作条件下液滴表面能的变化 Fig.10 Variations in surface energy of droplets for different physical properties and operating conditions |
表面能随着表面张力系数的减小而减小,表面张力系数较小时液滴的铺展面积较大,表面能的增加量较大,且由于其不发生回缩,其表面能达最大值后保持不变。随着表面张力系数的增加,在撞击的初始阶段液滴表面能增加的速率变大。
由图 4(c)、图 7(c)和式(19)均可知,随着撞击速度的增加,液滴铺展直径和铺展面积增加,从而带来液滴的表面能增加量的增大。此外,随着撞击速度的增大,铺展过程中液滴表面能增加的速率变大。
2.3.2 动能因仅使用高速相机无法获取液滴内每个质点的速度,故使用液滴质心的速度计算液滴动能,如式(21)所示。
| $ E_{\mathrm{K}}=\frac{1}{2} \rho\left(\frac{1}{6} \pi D_{0}^{3}\right) U_{\mathrm{C}}^{2} $ | (21) |
式中UC为液滴质心的速度。
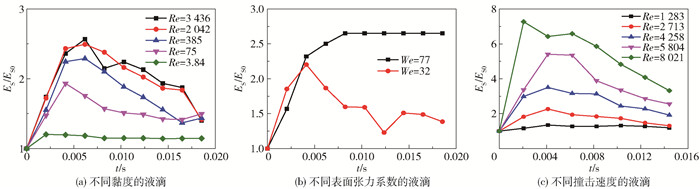
图 11(a)显示出具有不同黏度的液滴的动能随时间先减小后增大的一般趋势。在撞击的初始阶段液滴动能减小的速率最大,随着黏度的增加,液滴在铺展过程中动能减小的速度加快,说明随着液滴黏度的增大,有更多的动能耗散在黏性中。
|
图 11 不同物性和操作条件下液滴动能的变化 Fig.11 Variations in kinetic energy of droplets for different physical properties and operating conditions |
图 11(b)为水和乙醇液滴在撞击过程中动能随时间的变化。可以看出,液滴在铺展过程中动能的减小量和减小的速率不随表面张力系数而变化。
图 11(c)为不同撞击速度下液滴动能随时间的变化。随着撞击速度的增加,液滴在铺展过程中动能减小的速度增大。撞击速度较大的液滴初动能较大,在表面张力和黏性力的作用下剩余能量更多,动能较大;并且撞击速度较大的液滴受到的黏性力较大,更多的动能耗散在黏性阻力中,致使其动能减小的速率增大。
2.3.3 黏性耗散可用式(22)计算液滴在撞击过程中能量耗散在黏性中的值
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{E_{\rm{V}}} = \int_0^t {\int_0^V \mu } \left( {2{{\left( {\frac{{\partial {U_x}}}{{\partial x}}} \right)}^2} + 2{{\left( {\frac{{\partial {U_y}}}{{\partial y}}} \right)}^2} + 2{{\left( {\frac{{\partial {U_z}}}{{\partial z}}} \right)}^2} + } \right.}\\ {{{\left( {\frac{{\partial {U_x}}}{{\partial y}} + \frac{{\partial {U_y}}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial {U_z}}}{{\partial y}} + \frac{{\partial {U_y}}}{{\partial z}}} \right)}^2} + {{\left( {\frac{{\partial {U_x}}}{{\partial z}} + \frac{{\partial {U_z}}}{{\partial x}}} \right)}^2})} \end{array}\\ {\rm{d}}V{\rm{d}}t \end{array} $ | (22) |
式中,Ux、Uy和Uz分别为液滴内流体在x、y和z方向的速度,但本文中无法获得液滴内部的速度分布以及速度的梯度随撞击时间的变化。液滴在撞击过程中能量耗散在黏性中的值可用式(23)计算
| $ E_{\mathrm{v}}=E_{\mathrm{so}}+E_{\mathrm{k} 0}-\left(E_{\mathrm{s}}+E_{\mathrm{K}}\right) $ | (23) |
定义能量耗散率如式(24)所示。
| $ \frac{E_{\mathrm{V}}}{E_{0}}=\frac{E_{\mathrm{V}}}{E_{\mathrm{S} 0}+E_{\mathrm{K} 0}} $ | (24) |
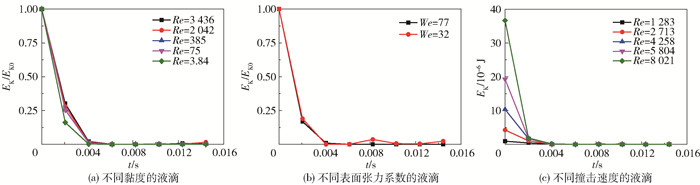
如图 12(a)所示,具有不同黏度的液滴的黏性耗散占总能量的比例先增加后几乎保持不变。在撞击的初始阶段,液滴黏性耗散的速率最大。由图 5(a)可知,当液滴的黏度增加1000倍时,液滴的铺展线速度减小为原来的0.61,液滴铺展线速度减小的程度远小于液滴黏度增大的程度,液滴内部速度梯度减小的程度远小于液滴黏度增大的程度,则根据式(22)可得液滴在撞击过程中的黏性耗散率和黏性耗散速率均随着黏度的增大而增大。
|
图 12 不同物性和操作条件下液滴黏性耗散的变化 Fig.12 Variations in viscosity dispersion of droplets for different physical properties and operating conditions |
图 12(b)为水和乙醇液滴的黏性耗散随时间的变化。由图 5(b)可知,当液滴的表面张力系数减小为原来的0.31时,液滴的铺展线速度增加1.18倍,液滴内的速度梯度相应也有所增加,则根据式(22)可得乙醇黏性耗散速率大于水液滴黏性耗散速率。
图 12(c)为液滴在不同撞击速度下的黏性耗散情况。由图 5(b)可知,液滴的撞击速度增加6.25倍时,液滴的最大铺展线速度增加3.14倍,液滴内部的速度梯度增加,则根据式(22)可得液滴在撞击过程中的黏性耗散率和黏性耗散速率均随着撞击速度的增大而增大。
2.3.4 能量的计算液滴的撞击过程与质量-弹簧-阻尼系统类似,因此建立液滴撞击的弹簧阻尼模型,液滴的质量为m,初始直径为D0,铺展直径为D,弹簧的弹性系数为k(N/m),阻尼器的阻尼系数为c(kg/s),根据牛顿第二定律可得
| $ \frac{\mathrm{d}^{2} D^{*}}{\mathrm{d} t^{2}}+\frac{c}{m} \frac{\mathrm{d} D^{*}}{\mathrm{d} t}+\frac{k}{m} D^{*}=0 $ | (25) |
根据初始条件D*(0)=0和实验结果可求得D*(t)的计算式如式(26)所示。
| $ \begin{array}{l} {D^ * }\left( t \right) = 0.39\mathit{R}{\mathit{e}^{0.12}}W{\mathit{e}^{0.27}}\left( {{{\rm{e}}^{ - 0.025\mathit{R}{\mathit{e}^{0.41}}W{e^{ - 0.57}}{t^ * }}} - } \right.\\ {{\rm{e}}^{ - 30\mathit{R}{\mathit{e}^{ - 0.17}}W{e^{ - 0.37}}{t^ * }}} \end{array} $ | (26) |
液滴在撞击过程中的形状与球冠类似,则液滴的铺展面积可用式(27)和(28)计算
| $ S=\pi\left(\left(\frac{D}{2}\right)^{2}+h^{2}\right) $ | (27) |
| $ h^{3}+\frac{3}{4} D^{2} h-D_{0}^{3}=0 $ | (28) |
式中,h为液滴的铺展高度。
可根据式(19)、式(1)、式(26)~(28)计算液滴表面能。由式(26)可求得液滴的铺展线速度进而求得液滴的动能。根据以上求得的液滴表面能和动能以及式(16)可求得液滴的黏性耗散。
图 13为液滴直径和能量的计算值与实验值对比。可以看出,液滴直径的计算值和实验值的平均误差约为15%(图 13(a)),液滴表面能的计算值和实验值的平均误差约为15%(图 13(b)),液滴动能的计算值和实验值的误差较大,最大误差约为50%(图 13(c)),液滴黏性耗散的计算值和实验值的误差小于15%(图 13(d))。
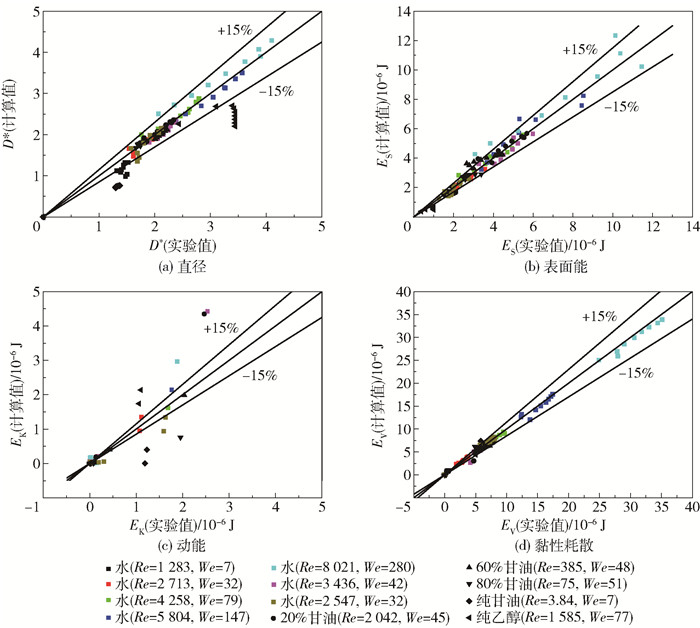
|
图 13 液滴直径和能量的计算值与实验值对比 Fig.13 Comparison of calculated and experimental values of droplet diameter and energy |
(1) 铺展直径和铺展面积随时间变化的一般趋势为先增大后减小,铺展线速度随时间变化的一般趋势为先在短时间内增加到最大值,随后逐渐减小到0。随着液滴黏度的增加,或表面张力的增大,或撞击速度的减小,液滴的铺展直径、铺展速度和铺展面积均减小。
(2) 在75 < Re < 9000,7 < We < 300时,可使用关系式Dmax*=We14和Smax*=0.203Re0.064We0.43分别预测液滴的最大铺展直径和最大铺展面积。
(3) 在液滴撞击的过程中,其表面能变化的一般趋势为先增大后减小,其动能变化的一般趋势为先减小后增大,其黏性耗散变化的一般趋势为先增大后保持不变。能量在黏性中的耗散主要发生在撞击的初始阶段。随着液滴黏度的增加,或表面张力系数的减小,或撞击速度的增加,黏性耗散的速率均增加。
| [1] |
王强, 郑宏飞, 厉彦忠. 横管降膜蒸发太阳能海水淡化装置的性能分析[J]. 太阳能学报, 2003, 24(3): 302-306. WANG Q, ZHENG H F, LI Y Z. The performance analysis on horizontal tube falling film evaporation solar desalination unit[J]. Acta Energiae Solaris Sinica, 2003, 24(3): 302-306. (in Chinese) DOI:10.3321/j.issn:0254-0096.2003.03.005 |
| [2] |
祝杰, 吴振元, 叶世超, 等. 喷淋塔内液滴运动及分布特性的研究[J]. 化工与医药工程, 2014, 35(2): 11-15. ZHU J, WU Z Y, YE S C, et al. Research on characteristics of droplet motion and distribution in spray tower[J]. Chemical and Pharmaceutical Engineering, 2014, 35(2): 11-15. (in Chinese) DOI:10.3969/j.issn.1008-455X.2014.02.004 |
| [3] |
LI N, ZHOU Q L, CHEN X, et al. Liquid drop impact on solid surface with application to water drop erosion on turbine blades, Part Ⅰ:Nonlinear wave model and solution of one-dimensional impact[J]. International Journal of Mechanical Sciences, 2008, 50(10/11): 1526-1542. |
| [4] |
AI T, MUDASSAR A M, CAI Z Q, et al. Liquid dispersion and gas absorption in a multi stage high speed disperser[J]. Chemical Engineering Journal, 2018, 352: 704-715. DOI:10.1016/j.cej.2018.07.076 |
| [5] |
MAO T, KUHN D C S, TRAN H. Spread and rebound of liquid droplets upon impact on flat surfaces[J]. AIChE Journal, 1997, 43(9): 2169-2179. DOI:10.1002/(ISSN)1547-5905 |
| [6] |
ZHANG X G, BASARAN O A. Dynamic surface tension effects in impact of a drop with a solid surface[J]. Journal of Colloid and Interface Science, 1997, 187(1): 166-178. DOI:10.1006/jcis.1996.4668 |
| [7] |
李维仲, 朱卫英, 权生林, 等. 液滴撞击水平固体表面的可视化实验研究[J]. 热科学技术, 2008, 7(2): 155-160. LI W Z, ZHU W Y, QUAN S L, et al. Visual experimental study on droplet impacted onto horizontal solid surface[J]. Journal of Thermal Science and Technology, 2008, 7(2): 155-160. (in Chinese) |
| [8] |
崔洁, 陆军军, 陈雪莉, 等. 液滴高速撞击固体板面过程的研究[J]. 化学反应工程与工艺, 2008, 24(5): 390-394. CUI J, LU J J, CHEN X L, et al. Study of liquid droplet impacting on a solid surface with high velocity[J]. Chemical Reaction Engineering and Technology, 2008, 24(5): 390-394. (in Chinese) DOI:10.3969/j.issn.1001-7631.2008.05.002 |
| [9] |
AN S M, LEE S Y. Maximum spreading of a shear thinning liquid drop impacting on dry solid surfaces[J]. Experimental Thermal and Fluid Science, 2012, 38: 140-148. DOI:10.1016/j.expthermflusci.2011.12.003 |
| [10] |
ABOUD D G K, KIETZIG A M. Splashing threshold of oblique droplet impacts on surfaces of various wettability[J]. Langmuir, 2015, 31(36): 10100-10111. DOI:10.1021/acs.langmuir.5b02447 |
| [11] |
CHANDRA S, AVEDISIAN C T. On the collision of a droplet with a solid surface[J]. Proceedings of the Royal Society of London[J]. Series A:Mathematical, Physical and Engineering Sciences, 1991, 432(1884): 13-41. DOI:10.1098/rspa.1991.0002 |
| [12] |
PASANDIDEH-FARD M, QIAO Y M, CHANDRA S, et al. Capillary effects during droplet impact on a solid surface[J]. Physics of Fluids, 1996, 8(3): 650-659. DOI:10.1063/1.868850 |
| [13] |
ŠIKALO Š, WILHELM H D, ROISMAN I V, et al. Dynamic contact angle of spreading droplets:experiments and simulations[J]. Physics of Fluids, 2005, 17(6): 062103. |
| [14] |
LUNKAD S F, BUWA V V, NIGAM K D P. Numerical simulations of drop impact and spreading on horizontal and inclined surfaces[J]. Chemical Engineering Science, 2007, 62(24): 7214-7224. DOI:10.1016/j.ces.2007.07.036 |
| [15] |
WANG Y X, CHEN S. Droplets impact on textured surfaces:mesoscopic simulation of spreading dynamics[J]. Applied Surface Science, 2015, 327: 159-167. DOI:10.1016/j.apsusc.2014.11.148 |
| [16] |
SCHELLER B L, BOUSFIELD D W. Newtonian drop impact with a solid surface[J]. AIChE Journal, 1995, 41(6): 1357-1367. DOI:10.1002/(ISSN)1547-5905 |
| [17] |
CLANET C, BÉGUIN C, RICHARD D, et al. Maximal deformation of an impacting drop[J]. Journal of Fluid Mechanics, 2004, 517: 199-208. DOI:10.1017/S0022112004000904 |
| [18] |
ROISMAN I V. Inertia dominated drop collisions. Ⅱ. An analytical solution of the Navier-Stokes equations for a spreading viscous film[J]. Physics of Fluids, 2009, 21(5): 052104. DOI:10.1063/1.3129283 |
| [19] |
CHEN R H, WANG H W. Effects of tangential speed on low-normal-speed liquid drop impact on a non-wettable solid surface[J]. Experiments in Fluids, 2005, 39(4): 754-760. DOI:10.1007/s00348-005-0008-6 |








