2. 对外经济贸易大学 国际经济贸易学院, 北京 100029;
3. 北京化工大学 信息科学与技术学院, 北京 100029;
4. 北京化工大学 智能过程系统工程教育部工程研究中心, 北京 100029
2. School of International Economics and Business, University of International Business and Economics, Beijing 100029;
3. College of Information Science & Technology, Beijing University of Chemical Technology, Beijing 100029;
4. Engineering Research Center of Intelligent PSE, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
Charnes等[1]于1978年首次提出数据包络分析(data envelopment analysis,DEA)方法,该方法优势在于无需确定的函数形式即可对生产效率进行分解。目前该模型被广泛用于评价经济增长效率、企业绩效、资源环境配置等诸多方面。然而传统DEA方法存在两个重要的约束限制,即强可处置性假设与决策单元(decision making unit,DMU)相互独立假设,前者主要指投入与产出成正向关联关系,后者主要指决策单元的投入或产出之间相互独立。
在基于传统DEA模型的强可处置性假设条件下,分析资源环境效率问题时往往忽略非期望产出(负效应)的影响,使得效率评价略显偏颇。因此,如何对传统模型进行有效改进成为学术界关注的焦点。目前,针对非期望产出的处理主要有以下两种思路:①对非期望产出的原始数据进行有效处理,即将诸如污染物等非期望产出视为投入,然后运用传统DEA方法进行效率评价;②对非期望产出进行弱处置性假设,构建环境DEA模型或环境DEA技术[2]。Chambers等[3]首次在评价行业环境效率中引入非期望产出(如污染物、CO2排放等),在对其进行弱可处置性假设后,基于径向DEA模型对行业环境效率进行测评。刘冰熙等[4]借助修正的三阶段Bootstrapped-DEA方法评估地方政府环境治理效率,结果发现我国地方政府环境治理存在比较严重的效率损失,治理效率值呈波浪态势且日趋恶化。郭四代等[5]运用三阶段DEA模型对中国区域层面的环境效率、变化趋势及其差异性等方面进行了全面评估。
传统DEA模型第二个重要假设表现在决策单元往往以自身效率最大化为目标约束,并不考虑其他决策单元的信息,因此造成效率评价过于片面。Sexton等[6]基于此问题,首次提出了交叉效率模型,其基本思想在于允许所有决策单元之间相互评价,每个决策单元选择一组最优的权重依次评价其他的决策单元,然后将每个决策单元的相互评价效率值集结成一个最终的评价结果。Doyle和Green[7]提出了仁慈型和进取型的二次目标模型对决策单元的权重进行约束,进而计算效率分数。刘学之等[8]基于我国钢铁企业的投入产出数据,运用DEA交叉效率模型评价钢铁产业的能源交叉效率。
尽管交叉DEA模型能够考量决策单元之间的关联,但在计算交叉评价指数时会较为主观地给予每一个评价向量相同的权重(1/n)。由于不同DMU间的相关性不尽相同,且它们对整个评价系统的贡献度有所差异,因此有些无效的评价信息会显著影响DEA模型的评估结果。目前,针对等权重赋值问题的处理方法,主要集中于对效率值进行模糊化处理,以此消除构建交叉互评矩阵的过度主观性问题。高明美等[9-10]构造了改进型直觉模糊熵的计算公式,并利用改进的方法确定区间属性权重以判别区间多属性决策。范建平等[11]定义了一种新的方法将三角模糊效率值转化为直觉模糊集,并用直觉模糊熵对模糊交叉效率进行计算,然后使用三元有向距离函数对全局模糊效率值排序。综上所述,已有文献虽然也对交叉互评指数的计算进行修正,但处理方法大都是引入新的参数并进行人为赋值,使得结果同样存在着一定的主观性。而交叉评价指数不准确的原因在于没有一个机制来区分信息有效程度。Adler和Golany[12]使用主成分分析法(principal component analysis,PCA)从投入产出数据上对变量进行降维,以剔除一些无效变量,使得DEA评价更为有效。基于这个思想,本文将主成分分析方法应用到交叉互评矩阵中,筛除交叉评价系统中冗余的信息;在尽量保持矩阵完整信息的基础上,用少量不相关的主成分来代替众多原始评价向量,并根据对信息矩阵的贡献程度为评价单元赋值,从而改善交叉环境模型的评估效率。
1 基于主成分分析法的DEA交叉模型的构建 1.1 环境DEA交叉模型如引言部分所述,传统的DEA模型没有考虑非期望产出物,与实际的生产情况相悖,如煤炭发电必然会产生二氧化碳,造纸行业必然会产生污水。在生产活动中,人们希望非期望产出越少越好,但这就与一般DEA模型假设产出为强可处置性相悖。因此,如果在产出中不将非期望产出与期望产出加以区分,则会使整个效率评价体系扭曲、无效。
假设在某个环境测评体系中有n个对象,则每一个对象j就是一个决策单元(zj)。其中有m种投入要素指标,d1种期望产出指标以及d2种非期望产出指标,则决策单元j的投入指标值xj、期望产出指标值yj和非期望产出指标值uj分别为
| $ {x_j} = \left( {{x_{1j}},{x_{2j}}, \cdots ,{x_{mj}}} \right),x \in R_ + ^{m \times n} $ |
| $ {y_j} = \left( {{y_1},{y_2}, \cdots ,{y_{d1}}} \right),y \in R_ + ^{{d_1} \times n} $ |
| $ {u_j} = \left( {{u_1},{u_2}, \cdots ,{u_{d2}}} \right),u \in R_ + ^{{d_2} \times n} $ |
依据一般环境DEA模型的设定[13],假设期望产出Y及非期望产出U同时具有弱可处置性的特征,即若(Y, U)∈P,则(αY, αZ)∈P,∀α∈(0, 1],其中,P表示生产可能性集合(生产技术)。也就是说,要减少非期望产出的唯一方法就是同比例减少期望产出的数量。如果假设生产技术呈现规模报酬不变的特性(constant return to scale,CRS),则环境Charnes,Cooper和Rhodes(CCR)模型的技术集合P可以表示为
| $ \begin{array}{l} \;\;\;\;\;P = \left\{ {\left( {X,Y,U} \right)|\sum\limits_{j = 1}^m {{\lambda _j}{x_{mj}} \le {x_m}} ,\sum\limits_{j = 1}^{{d_1}} {{\lambda _j}{y_{j{d_1}}} \ge } } \right.\\ \left. {{y_m},\sum\limits_{j = 1}^{{d_2}} {{\lambda _j}{u_{j{d_2}}} = {u_m}} } \right\} \end{array} $ | (1) |
即在生产技术P的条件下,投入m种要素X,可以产出d1种期望产出Y以及d2种非期望产出U。其中,λi为决策单元向量的权重。如果生产技术呈现规模报酬可变(variable return to scale,VRS)的特性,则需要额外加入Σiλi=1的条件,环境CCR模型变成环境Banker,Charnes和Cooper(BCC)模型。根据Färe等[14]提出的处理方法,式(1)中生产技术可以转化为环境CCR模型
| $\min \theta \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\mathit{\boldsymbol{X\lambda }} + {S^ + } = {x_{m0}}\\ \ \ \ \ \ \ \ \ \mathit{\boldsymbol{Y\lambda }} - {S^ - } = {y_{m0}}\\ \ \ \ \ \ \ \ \ \mathit{\boldsymbol{U\lambda }} = \theta {u_{k0}}\\ {\lambda _k},{S^ + },{S^ - } \ge 0 $ | (2) |
式中,X、Y、U分别为投入要素、期望产出以及非期望产出矩阵;λ在这里作为要素投入的权重;S-、S+分别为产出松弛变量与投入松弛变量;θ表示评价单元的环境效率,即环境评价指数(environmental performance index,EPI)。θ数值越大,说明该评价单元在控制非期望产出量方面没有更多的提升空间,则认定该单元的环境表现越好;反之则相反。可以看出,环境CCR模型的侧重点是在控制非期望产出U上。
接下来使用Charnes Cooper变换,将式(2)转换为其对偶问题
| ${\rm{Max}}\mathit{\boldsymbol{\rho }} = \sum\limits_{k = 1}^{{d_1}} {{\mathit{\boldsymbol{\alpha }}_k}{\mathit{\boldsymbol{Y}}_k}} - \sum\limits_{m = 1}^M {{\mathit{\boldsymbol{\beta }}_m}{\mathit{\boldsymbol{X}}_m}} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\sum\limits_{k = 1}^{{d_1}} {{\alpha _{ki}}{Y_{ki}}} - \sum\limits_{m = 1}^M {{\beta _{mi}}{X_{mi}}} - \sum\limits_{s = 1}^{{d_2}} {{\gamma _{si}}{U_{si}}} \le 0\\ \ \ \ \ \ \ \sum\limits_{s = 1}^{{d_2}} {{\gamma _{si}}{U_{si}}} = 1,i = 1,2, \cdots ,N\\ {\mathit{\boldsymbol{\alpha }}_k},{\mathit{\boldsymbol{\beta }}_m} \ge {\bf{0}};{\mathit{\boldsymbol{\gamma }}_s}{\rm{为自由变量}} $ | (3) |
式中,目标方程ρ的计算结果与式(2)中的θ相同,都代表了决策单元的环境效率;α、β和γ分别为投入要素、期望产出及非期望产出向量X、Y和U的权重。定义ρ达到最大值时投入产出向量的最优权重组合为L*=(α*,β*,γ*),L*为m+d1+d2维的向量。
基于Sexton等[6]的概念,定义交叉环境效率指数为
| $ \rho _{ij}^{{\rm{cross}}} = \frac{{\mathit{\boldsymbol{Y}}_{{d_1}}^{\rm{T}}\mathit{\boldsymbol{\alpha }}_{{d_2}}^*}}{{\mathit{\boldsymbol{X}}_m^{\rm{T}}\mathit{\boldsymbol{\beta }}_m^* - \mathit{\boldsymbol{U}}_{{d_2}}^{\rm{T}}\mathit{\boldsymbol{\gamma }}_{{d_2}}^*}} $ | (4) |
由式(4)可以看出,当j=i时,ρij=ρ;交叉环境评价指数退化为一般环境效率指数,即部门j通过自己的最优权重Lj*计算出EPI指数,记为环境自评价指数;当j≠i时,部门j的效率值是通过i部门的最优权重Li*计算,所计算出的EPI称为环境交叉评价指数,i, j=1, 2, 3, …, n。
最后,由交叉指数可以构成一个环境交叉评价矩阵CEM(cross efficient matrix,CEM),表示为
| $ {\mathit{\boldsymbol{C}}_{{\rm{EM}}}} = \left( {\begin{array}{*{20}{c}} {{\rho _{11}}}& \cdots &{{\rho _{1n}}}\\ \vdots&\ddots&\vdots \\ {{\rho _{n1}}}& \cdots &{{\rho _{nn}}} \end{array}} \right) $ |
其中,对角线上的元素即为一般环境效率指数,而非对角线上元素为交叉环境评价指数,如ρ1j表示从第j个决策单元的角度对第一个决策单元的评价。按照行方向计算每一个评价单元的算术平均值ρi,则ρi就是一般概念下的环境交叉互评指数
| $ {{\bar \rho }_i} = \frac{{\sum\limits_{i = 1}^n {{\rho _{ij}}} }}{n} $ | (5) |
主成分分析方法是由Hotelling[15]于1933年提出一种压缩高维矩阵,并从中提取数据分散特征(variation)的统计分析技术。该方法的优势在于将原始的存在着相关性的n维解释变量转化为p维直交的综合解释变量,且n≫p,从而达到降维的目的。基于主成分分析法的特点,对交叉评价矩阵进行降维,用少量不相关的主成分来代替众多原始评价向量,从而改善交叉环境模型的评估效率。
在通常情况下,由于各解释变量的量纲不同,会造成主成分分析的偏差,因此需要对数据提前作预处理。然而,交叉环境DEA模型计算的结果,即交叉互评矩阵中的元素代表效率值,都是无量纲且分布于(0, 1]之间,因此不需要额外进行归一化处理。
基于主成分分析的交叉评价指数构建具体步骤如下。
1) 设环境CEM矩阵中的互评向量为ρ = (ρ1,ρ2,…,ρn),计算其相关系数矩阵R。
2) 将矩阵R进行分解,计算其特征值w1≥w2≥…≥wn≥0以及相对应标准化的特征向量e1,e2,…,en。计算公式为
| $ \left( {\mathit{\boldsymbol{R}} - {w_j}E} \right) \times {\mathit{\boldsymbol{e}}_j} = 0 $ | (6) |
3) 使用评价指数ρ与特征向量e,计算主成分指标数据矩阵ρPC。则第i个主成分可以表示为
| $ \mathit{\boldsymbol{\rho }}_i^{{\rm{PC}}} = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{\rho }} = {e_{1i}}{\rho _1} + {e_{2i}}{\rho _2} + \cdots + {e_{pi}}{\rho _p} $ | (7) |
4) 根据各主成分的贡献率,选取前p个作为参考指标。假设它们已经基本反映了原评价体系的主要信息,之后计算环境综合评价指标
| $ {\mathit{\boldsymbol{\rho }}^{{\rm{PC}}}} = \sum\limits_{i = 1}^p {\mathit{\boldsymbol{\rho }}_i^{{\rm{PC}}}} $ | (8) |
可以看出,本文计算出的主成分由特征向量和原始的互评向量作线性组合而成,它包含了原来CEM矩阵中的所有信息。此外,各主成分向量间是正交的关系,即(ρjPC)T×ρiPC=0,j≠i。各主成分的方差为Var(ρiPC) =eiTRei,i=1, 2,…,n。按照方差的大小,依次称其为第一主成分、第二主成分、…,这些主成分按照其对整个矩阵方差的贡献程度逐级递减。因此,在实际应用时,往往只使用前几个贡献度大的成分。如果要避免信息损失,可以按照累积贡献率100%的原则选取主成分变量。
2 算例分析以往用来衡量产业(部门)环境绩效表现的指标有3个,即能源强度(能源消耗量与GDP的比值)、排放强度(CO2排放量与GDP的比值)、以及碳因子(CO2排放量与能源消耗量的比值)。但是这些指标只能对投入、产出数据进行二维的考量,无法综合考虑所有因素。此外,化石能源是产生二氧化碳气体的主要原料,而中国是化石燃料消耗的大国。因此,本文采用北京市统计局发布的“2012年北京市投入产出表”以及《中国能源统计年鉴2013》中42个部门化石燃料的消耗和碳排放量,通过环境交叉DEA模型对行业的环境表现指数(EPI)进行度量,并将一般模型结果与改进模型结果进行对比。
2.1 数据来源及预处理如表 1所示,行业总量为42,即决策单元数量n为42。其中,包含第一产业部门1个,第二及第三产业部门分别为27个、14个。
| 下载CSV 表 1 部门名称及代码 Table 1 Department name and code |
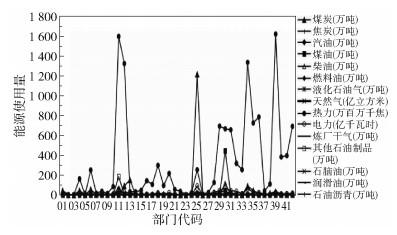
本文针对行业的环境表现效率进行评估,主要讨论的是在生产过程中对于非期望产出的控制。因此如表 2所示,投入指标X选取为各部门生产所消耗的一次(化石)能源数量,包含煤炭、焦炭、汽油、煤油等15种主要能源。各部门的能源消耗量见图 1。
| 下载CSV 表 2 输入、输出数据 Table 2 Input and output data |
|
图 1 能源使用量 Fig.1 Main energy uses |
期望产出指标Y使用的是每一个部门的行业总产值,即投入15种一次能源后所产生的正向经济效益;而非期望产出指标U选取为每一个部门伴随着生产所排放出二氧化碳气体的数量。本文采用如下公式对各部门的CO2排放总量进行估算
| $ {U_j} = {\mathit{\Sigma }_i}{X_{ij}}{\delta _i} $ | (9) |
式中,Uj为j部门的排放总量;Xij为j部门的第i种能源的投入量(需要折算为标准煤);δi为能源i的排放系数(以燃烧热值法为主,详见表 3)。
| 下载CSV 表 3 能源排放系数 Table 3 Energy emission coefficients |
由于个别产业的投入数据不满足DEA模型的基本要求,因此需要进行预处理。
令xij表示第j个行业消耗第i种能源的数量,则转换后数据变为
| $ {x_{ij}} = \frac{{{x_{ij}} - \min \left( {{x_{1j}},{x_{2j}}, \cdots ,{x_{nj}}} \right)}}{{\max \left( {{x_{1j}},{x_{2j}}, \cdots ,{x_{nj}}} \right) - \min \left( {{x_{1j}},{x_{2j}}, \cdots ,{x_{nj}}} \right)}} $ | (10) |
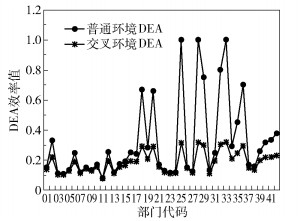
首先,使用一般环境CCR模型(假设行业规模收益不变),对“2012年北京市投入产出表”中42个部门的环境表现指数进行自评;再利用一般交叉环境模型对42个部门进行交叉互评。两种模型的效率计算结果见图 2。
|
图 2 自评结果和互评结果对比 Fig.2 Comparison of the results of self-evaluation and mutual evaluation |
由图 2可知,有3个部门的环境表现达到了DEA有效(效率值为1),分别为电力、热力的生产和供应,建筑业以及金融业(部门代码为分别25、28和33)。在引入互评机制后,点状线为交叉环境效率指数的结果。可以看出,行业效率值在经过其他决策单元的互评后,出现了显著的下降。排名在前三的依旧为电力、热力的生产和供应,建筑业以及金融业,但是已经可以明显区分它们之间的排名,且与达到DEA有效相距甚远。
随后,基于交叉评价矩阵(表 4)的计算结果,再通过式(6)、(7)对互评系统的主成分进行计算;其中,CEM矩阵对角线上元素的数值为一般环境DEA模型所计算出的行业自评分数。由表 5的结果可知,前两个主成分ρ1PC和ρ2PC对方差的贡献率已经达到93.7%,后面成分的信息对互评矩阵的解释作用微乎其微。因此,本文保留原互评向量组ρ的前两个主成分。
| 下载CSV 表 4 42部门交叉评价结果 Table 4 42 sector cross evaluation matrix |
| 下载CSV 表 5 主成分结果 Table 5 Results of PCA |
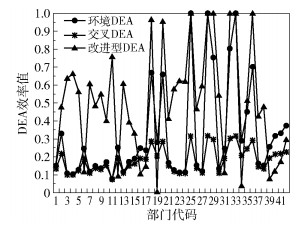
继续根据式(8)计算环境综合评价指标,然后将3个模型的计算结果进行对比。从图 3可知,从效率值本身分析,基于主成分分析方法改进的环境绩效指数与一般交叉DEA模型结果相差较大。其中,有21个行业的EPI指数都在0.5以上,达到DEA有效的部门数量有6个,其行业代码分别为25、28、29、32、33、36;而传统交叉模型计算出的结果中,只有5个行业EPI指数在0.3以上,数值上明显低估了行业效率。由于效率值只是反映行业间相对的变化,更为重要的是行业间的绩效排序情况。表 6列出了环境CCR模型、交叉环境模型以及改进型交叉环境模型的计算结果对比。
|
图 3 3种模型环境表现指数 Fig.3 Environmental performance improvement index |
| 下载CSV 表 6 3种模型的排名对比 Table 6 Comparison of the three models |
从表 6取排名最前和最后的6个部门进行分析。首先观察一般环境模型(模型a)与改进型交叉模型(模型c)的结果,发现两者涵盖部门差异较小,排名前六位的全部涵盖。而排名后六位部门中前者包含废品废料业、金属制品修理服务业以及石油开采业(代码分别为3、23、24);后者包含了交通设备业、交通运输与仓储服务业以及居民服务业(代码分别是18、30、38)。其次,再对比交叉模型(模型b)与改进型模型(模型c),排名前六位的部门各有一个不同:交通运输业(代码18,交叉模型)与金融业(代码33,改进型模型);而排名后六位的则相差了2个部门:交叉模型中含有废品废料业(代码23)与石油和天然气开采业(代码3),而改进型模型中包含了运输业及居民服务业(代码分别为18、38)。为进一步验证3种方法测度下部门环境效率排序是否存在显著差异,运用非参数的Wilcoxon rank-sum检验,该检验的原假设为待检验的两组行业效率排名(rank)没有显著性差异。鉴于使用的3个序列的样本量都较大(n=42),因此本文假定Wilcoxon统计量服从标准正态分布。结果如表 7所示。
| 下载CSV 表 7 Wilcoxon检验结果 Table 7 Wilcoxon test results |
以基于PCA的交叉环境模型的计算结果作为基准组。如果选取5%的显著性水平下进行分析,环境CCR模型与一般交叉模型的计算结果都与基准组的行业效率结果有显著的不同(P值分别为0.04与0.00),且交叉模型的秩和统计量比环境模型的值要更大。
综上所述,基于PCA方法得到的改进型交叉评价指数,其计算结果无论与传统环境模型还是一般交叉模型对比,差异性都非常显著。究其原因,可能在于传统方法不是没有充分利用信息,就是对信息使用过于主观,造成了评价单元效率的扭曲。
3 结束语传统交叉DEA模型通过交叉评价矩阵对决策单元效率进行评估时,往往是使用简单的算术平均方法。这种等权重的做法比较主观且没有充分利用整个评价系统的信息,造成DEA分数的无效性。本文提出一种改进型的互评指数计算方法,利用主成分分析方法筛除CEM矩阵中的冗余信息;在尽量保证互评矩阵信息完整性的基础上,用少量主成分分数来计算决策单元的效率值,从而改善交叉DEA模型的评估效率。
真实算例的结果表明,改进型方法计算出的行业效率值与传统交叉评价方法有着显著不同。由于没有充分利用CEM中的信息,环境CCR模型与一般交叉模型的计算结果出现了较大偏差,明显低估了行业的环境绩效指数。当然,本文提出的方法同样可以应用于非径向(non-radial)的DEA模型假设,还有待后续研究。
| [1] |
CHARNES A, COOPER W W, RHODES E. Measuring the efficiency of decision making units[J]. European Journal of Operational Research, 1978, 2(6): 429-444. DOI:10.1016/0377-2217(78)90138-8 |
| [2] |
ZHOU P, ANG B W, POH K L. Measuring environmental performance under different environmental DEA technologies[J]. Energy Economics, 2008, 30(9): 1-14. |
| [3] |
CHAMBERS R G, FÄRE R, GROSSKOPF S. Productivity growth in APEC countries[J]. Pacific Economic Reviews, 1996, 1(3): 181-190. DOI:10.1111/per.1996.1.issue-3 |
| [4] |
刘冰熙, 王宝顺, 薛钢. 我国地方政府环境污染治理效率评价-基于三阶段Bootstrapped DEA方法[J]. 中南财经政法大学学报, 2016(1): 89-95. LIU B X, WANG B S, XUE G. On assessment of public spending efficiency of environment protection in local China:based on three-stage Bootstrapped DEA[J]. Journal of Zhongnan University of Economics and Law, 2016(1): 89-95. (in Chinese) DOI:10.3969/j.issn.1003-5230.2016.01.011 |
| [5] |
郭四代, 仝梦, 郭杰, 等. 基于三阶段DEA模型的际真实环境效率测度与影响因素分析[J]. 中国人口·资源与环境, 2018, 28(3): 106-116. GUO S D, TONG M, GUO J, et al. Measurement and influencing factors of inter-provincial real environmental efficiency based on three-stage DEA model[J]. China Population, Resources and Environment, 2018, 28(3): 106-116. (in Chinese) |
| [6] |
SEXTON T R, SILKMAN R H. Data envelopment analysis:critique and extensions[M]. San Francisco: Jossey-Bass, 1986.
|
| [7] |
DOYLE J, GREEN R. Efficiency and cross-efficiency in DEA:derivations, meanings and uses[J]. Journal of the Operations Research Society, 1994, 45(5): 567-578. DOI:10.1057/jors.1994.84 |
| [8] |
刘学之, 黄敬, 王玉. 基于DEA交叉效率模型的钢铁行业能源效率分析[J]. 管理世界, 2017(10): 182-183. LIU X Z, HUANG J, WANG Y. A study of steel industry:based on the cross-efficiency DEA model[J]. Management World, 2017(10): 182-183. (in Chinese) DOI:10.3969/j.issn.1002-5502.2017.10.017 |
| [9] |
高明美, 孙涛, 朱建军. 一种改进的直觉模糊熵公理化定义和构造公式[J]. 控制与决策, 2014, 29(3): 470-474. GAO M M, SUN T, ZHU J J. Revised axiomatic definition and structural formula of intuitionistic fuzzy entropy[J]. Control and Decision, 2014, 29(3): 470-474. (in Chinese) |
| [10] |
高明美, 孙涛, 朱建军. 基于改进熵和新得分函数的区间直觉模糊多属性决策[J]. 控制与决策, 2016, 31(10): 1757-1764. GAO M M, SUN T, ZHU J J. Interval-valued intuitionistic fuzzy multiple attribute decision-making method based on revised fuzzy entropy and new scoring function[J]. Control and Decision, 2016, 31(10): 1757-1764. (in Chinese) |
| [11] |
范建平, 薛坤, 吴美琴. 基于直觉模糊熵的交叉评价方法[J]. 计算机科学, 2018, 45(2): 280-286. FAN J P, XUE K, WU M Q. Cross evaluation method based on intuitionistic fuzzy entropy[J]. Computer Science, 2018, 45(2): 280-286. (in Chinese) |
| [12] |
ADLER N, GOLANY B. Evaluation of deregulated airline networks using data envelopment analysis combined with principal component analysis with an application to Western Europe[J]. European Journal of Operational Research, 2001, 132(2): 260-273. DOI:10.1016/S0377-2217(00)00150-8 |
| [13] |
TYTECA D. On the measurement of the environmental performance of firms-a literature review and a productive efficiency perspective[J]. Journal of Environmental Management, 1996, 46: 281-308. |
| [14] |
FÄRE R, GROSSKOPF S. Modeling undesirable factors in efficiency evaluation:comment[J]. European Journal of Operational Research, 2004, 157: 242-245. DOI:10.1016/S0377-2217(03)00191-7 |
| [15] |
HOTELLING H. Analysis of a complex of statistical variables into principal components[J]. Journal of Educational Psychology, 1933, 24(6): 417-520. DOI:10.1037/h0071325 |








