2. 中国科学院数学与系统科学研究院 应用数学研究所, 北京 100190;
3. 北京一〇一中学, 北京 100091
2. Institute of Applied Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190;
3. Beijing 101 Middle School, Beijing 100091, China
非线性系统的复杂行为(混沌行为)是非线性系统动力学研究的主要问题之一。一般来说,混沌行为有3个主要特征,即初值敏感、拓扑混合和周期解稠密[1],其中周期解稠密意味着在混沌系统中存在着无穷多个周期轨道,这些周期轨道对混沌系统的动力学性质起着决定性的作用:①类似于康托集合,混沌吸引子也是相空间剔除所有周期解后的补集,通过研究周期轨道的动态可以了解混沌吸引子的空间结构[2];②大周期的周期轨道构成了混沌吸引子的基本框架,因此可以用大周期的周期轨道来估计混沌系统的拓扑熵和Lyapunov指数[3];③周期倍分支道路是了解混沌系统由有序通向无序的一条最主要的道路,因此探索周期倍分支有助于了解系统从有序到无序的过程[4];④由于周期解的稠密性,大周期的周期解通常构成了混沌现象的吸引域,所以通过对该区域实施规避可以达到混沌控制的目的[5]。
然而,混沌系统中周期解是鞍点型的,即这些周期解的Floquet乘子既有正值又有负值,所以这些周期解都是不稳定的。这一独特的性质使得寻找这些周期解具有计算上的难度,普通的数值模拟算法(如龙格-库塔方法)无法发现这些周期轨道。另外由于混沌系统的周期解是稠密的,这些周期解的吸引空间和排斥空间都很小,从而对基于不动点理论的算法提出了挑战。
在多项式动力系统中,寻找周期轨道是一个传统的研究课题[6]。由于混沌系统强非线性和初值敏感的特性,虽然目前已有很多寻找周期解的数值方法,如同伦算法[7]、打靶法[8]及相空间探索法等,但是这些算法普遍收敛性较差,寻找周期解的能力有限,因此很难被应用到混沌系统中。
本文提出一种计算混沌系统中不稳定周期解的新算法,首先通过泰勒展开法得到混沌系统的离散化方程,然后针对特定周期的不稳定周期解构造一个目标函数,使得目标函数的极小值点(0值点)对应系统的一个周期轨道。为了使目标函数能够尽快收敛到混沌系统的不稳定周期轨道,提出一套新的寻找初始点的算法,即伪周期算法,通过在混沌吸引子中寻找伪周期点,得到在伪周期轨道附近存在的一个真正的周期轨道,再将伪周期轨道作为最优化算法的初值,从而将寻找混沌系统周期解的问题转化为一个最优化问题。最后以具有代表性的混沌系统Lorenz系统[9]为例,运用本文提出的新方法,通过寻找该系统中的朴素周期、超大周期以及倍周期的周期解来验证本文方法的有效性。
1 寻找不稳定周期解的数值方法Lorenz系统中存在混沌现象,该系统如式(1)
| $ \left\{ \begin{array}{l} x' = \sigma \left( {y - x} \right)\\ y' = - xz + rx - y\\ z' = xy - bz \end{array} \right. $ | (1) |
式中,参数σ=10,r=28,b=
下面针对系统(1)给出寻找不稳定周期解的过程以及优化策略。
1.1 伪周期解首先应用时间步长Δt,通过泰勒展开将Lorenz系统离散化,得到Lorenz系统的迭代格式
| $ \left\{ \begin{array}{l} {x_{n + 1}} = F\left( {{x_n}} \right) = {x_n} + {{x'}_n}\Delta t + \frac{1}{2}{{x''}_n}\Delta {t^2} + \frac{1}{6}{x^{\prime \prime \prime }}_n\Delta {t^3}\\ {y_{n + 1}} = G\left( {{y_n}} \right) = {y_n} + {{y'}_n}\Delta t + \frac{1}{2}{{y''}_n}\Delta {t^2} + \frac{1}{6}{y^{\prime \prime \prime }}_n\Delta {t^3}\\ {z_{n + 1}} = H\left( {{z_n}} \right) = {z_n} + {{z'}_n}\Delta t + \frac{1}{2}{{z''}_n}\Delta {t^2} + \frac{1}{6}{z^{\prime \prime \prime }}_n\Delta {t^3} \end{array} \right. $ | (2) |
式(2)中,迭代序列xn、yn、zn的一阶导数x′n、y′n、z′n分别为
| $ \left\{ \begin{array}{l} {{x'}_n} = 10{y_n} - 10{x_n}\\ {{y'}_n} = 28{x_n} - {y_n} - {x_n}{z_n}\\ {{z'}_n} = - \frac{8}{3}{z_n} + {x_n}{y_n} \end{array} \right. $ | (3) |
二阶导数x″n、y″n、z″n分别为
| $ \left\{ \begin{array}{l} {{x''}_n} = 380{x_n} - 110{y_n} - 10{x_n}{z_n}\\ {{y''}_n} = - 308{x_n} + 281{y_n} + 13\frac{2}{3}{x_n}{z_n} - 10{y_n}{z_n} - x_n^2{y_n}\\ {{z''}_n} = \frac{{64}}{9}{z_n} - 11\frac{2}{3}{x_n}{y_n} + 28x_n^2 + 10y_n^2 - x_n^2{z_n} \end{array} \right. $ | (4) |
三阶导数x'''n、y'''n、z'''n分别为
| $ \left\{ \begin{array}{l} {x^{\prime \prime \prime }}_n = - 6\;880{x_n} + 3\;910{y_n} + 36\frac{2}{3}{x_x}{z_n} - 100{y_n}{z_n} - 10x_n^2{y_n}\\ {y^{\prime \prime \prime }}_n = 10\;948{x_n} - 3\;361{y_n} - 734\frac{1}{9}{x_n}{z_n} + 173\frac{1}{3}{y_n}{z_n} + \\ \;\;\;\;\;\;\;\;\;10{x_n}z_n^2 - 30{x_n}y_n^2 + 31\frac{2}{3}x_n^2{y_n} - 28x_n^3 + x_n^3{z_n}\\ {z^{\prime \prime \prime }}_n = 18\frac{{26}}{{27}}{z_n} + 1\;272\frac{1}{9}{x_n}{y_n} - 942\frac{2}{3}x_n^2 - 156\frac{2}{3}y_n^2 + \\ \;\;\;\;\;\;\;\;\;17\frac{1}{3}x_n^2{z_n} - 40{x_n}{y_n}{z_n} - x_n^3{y_n} \end{array} \right. $ | (5) |
对于迭代方程(1),当通过迭代得到的xn、yn、zn满足式(6)时,得到式(7)。
| $ \begin{array}{l} \;\;\;\;\;\;\min \left\{ {{{\left( {{x_n} - {x_1}} \right)}^2} + {{\left( {{y_n} - {y_1}} \right)}^2} + {{\left( {{z_n} - {z_1}} \right)}^2}} \right\} < \varepsilon = \\ {10^{ - 2}} \end{array} $ | (6) |
| $ {\left[ {{x_1},{y_1},{z_1}, \cdots ,{x_n},{y_n},{z_n}} \right]^{\rm{T}}} $ | (7) |
将式(7)记作向量A,A即为Lorenz系统的伪周期解。
1.2 最优化策略本文优化问题所涉及的是大周期的周期轨道,迭代矩阵是高阶矩阵,计算机运行不仅耗时而且会产生误差累加,使迭代过程变缓、精度降低。最速下降法不需要计算矩阵的逆,并且算法相对简单,收敛性更好,因此本文选择最速下降法[10]来减小计算误差、提高计算精度。
针对伪周期解构造出目标函数φ
| $ \begin{array}{l} \;\;\;\;\;\;\varphi \left( {\mathit{\boldsymbol{A}},\Delta t} \right) = \sum\limits_{i = 2}^n {{{\left[ {{x_i} - F\left( {{x_{i - 1}},{y_{i - 1}},{z_{i - 1}}} \right)} \right]}^2}} + \left[ {{y_i} - } \right.\\ {\left. {G\left( {{x_{i - 1}},{y_{i - 1}},{z_{i - 1}}} \right)} \right]^2} + {\left[ {{z_i} - H\left( {{x_{i - 1}},{y_{i - 1}},{z_{i - 1}}} \right)} \right]^2} \end{array} $ | (8) |
显然式(8)的最小值点对应系统的周期解。通过最速下降法对目标函数式(8)进行优化,当目标函数值不再减小时,就得到了Lorenz系统的不稳定周期解。
1.3 算法实施将求解伪周期解的过程以及最优化方法转化为计算机语言,通过Matlab实现。求解周期解的具体步骤如下。
1) 寻找伪周期解。给定Lorenz系统的一个初始点(x1, y1, z1),并将其代入迭代方程(1),当(xn, yn, zn)满足式(6)时,得到
| $ \mathit{\boldsymbol{A}} = {\left[ {{x_1},{y_1},{z_1}, \cdots ,{x_n},{y_n},{z_n}} \right]^{\rm{T}}} $ |
2) 固定步长Δt,利用式(9)对向量A作最速下降优化
| $ {\mathit{\boldsymbol{A}}_{n + 1}} = {\mathit{\boldsymbol{A}}_n} - h{\left[ {\frac{{\partial \varphi }}{{\partial {x_1}}},\frac{{\partial \varphi }}{{\partial {y_1}}},\frac{{\partial \varphi }}{{\partial {z_1}}}, \cdots ,\frac{{\partial \varphi }}{{\partial {x_n}}},\frac{{\partial \varphi }}{{\partial {y_n}}},\frac{{\partial \varphi }}{{\partial {z_n}}}} \right]^{\rm{T}}} $ | (9) |
将An+1代入式(8),如果φ(An+1, Δt)<φ(An, Δt),说明目标函数值减小,则令An=An+1,新的An即为优化的伪周期解;反之令h=0.1h(h=0.1),代入式(9),得到新的An+1。如此循环往复,直至h<10-6,结束对A的优化。
3) 固定向量A,利用式(10)对步长Δt进行最速下降优化
| $ \Delta {t_{n + 1}} = \Delta {t_n} + h\frac{{{\partial ^2}\varphi \left( {\mathit{\boldsymbol{A}},\Delta {t_{n + 1}}} \right)/\partial \Delta {t^2}}}{{\left| {{\partial ^2}\varphi \left( {\mathit{\boldsymbol{A}},\Delta {t_{n + 1}}} \right)/\partial \Delta {t^2}} \right|}} $ | (10) |
将Δtn+1代入式(8)得到目标函数值,如果φ(A, Δtn+1)<φ(A, Δtn),说明目标函数值减小,则令Δtn=Δtn+1,即得到一个新的步长;反之令h=0.1h(h=0.1),将h代入式(10)得到新的Δtn+1。如此循环往复,直至h<10-6,结束对Δt的优化。
4) 当且仅当目标函数值不再减小时,停止所有优化,此时的A就是Lorenz系统的不稳定周期解。
2 数值模拟结果与分析按照1.3节中计算不稳定周期解的步骤,利用计算机运算得到了130个Lorenz系统的不稳定周期解,从中挑选出3种具有代表意义的周期解来进行对比分析。
2.1 朴素周期朴素周期也称为最小周期,是周期解中周期最短的周期。在得到的所有周期数据中挑选出来的最小周期T=231,图 1是T=231时优化前后的周期轨道图,表 1是图 1中优化前后的主要数据对比。
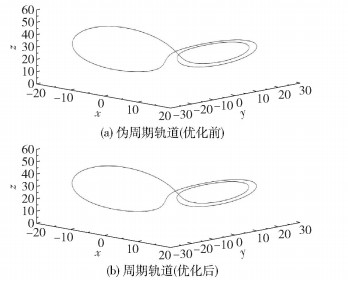
|
图 1 T=231时优化前后的朴素周期轨道图 Fig.1 Simple periodic orbit map before and after optimization |
| 下载CSV 表 1 优化前后朴素周期数据对比 Table 1 Comparison of simple periodic data before and after optimization |
从图 1和表 1看出,通过最速下降法对伪周期解优化后,目标函数初值的初始点由(7.981 9,-0.231 4, 34.697 8)优化为(7.346 9,-0.599 3, 33.950 1),周期数T不变,时间步长Δt不变,目标函数值由0.092 5降为7.802 7×10-4,优化后达到预期效果。
2.2 超大周期超大周期是指混沌吸引子中周期非常长的周期解。从得到的周期数据中挑选出来的最大周期T=9 646,图 2是T=9 646时优化前后的周期轨道图,表 2为图 2中优化前后的主要数据对比。
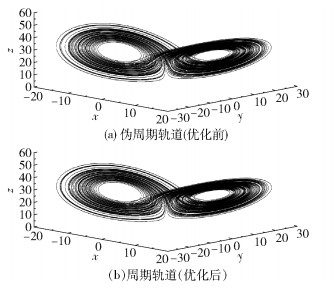
|
图 2 T=9 646时优化前后的超大周期轨道图 Fig.2 Large periodic orbit map before and after optimization |
| 下载CSV 表 2 优化前后的超大周期数据对比 Table 2 Comparison of large cycle data before and after optimization |
由图 2和表 2看出,目标函数初值的初始点由(5.154 5, 6.887 2, 19.553 4)优化为(5.164 7, 7.063 5, 19.171 6),周期数T不变,时间步长Δt不变,误差由0.082 3降至0.003 2。目标函数值虽然有所减小,但没有达到预期效果,说明算法中还存在有待优化的地方。
2.3 倍周期在得到的130个周期解数据中,挑选出周期具有倍数关系的两组周期,由于高阶近似以及迭代计算中会产生一定误差,设定如下倍数规则:如果存在周期n1、n2(n1<n2),并且满足n2=kn1±10(k∈N),则称n1、n2构成了一组倍周期。按照这一规则挑选出两组周期解,其周期分别为T=670和T=1 337与T=1 216和T=2 423。
(1) T=670和T=1 337。由最速下降方法得到两组倍周期轨道图,第一组轨道图如图 3所示。
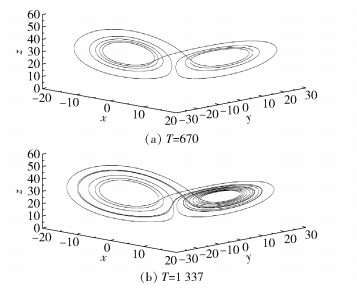
|
图 3 T=670和T=1 337的周期轨道图 Fig.3 The periodic orbits for T=670 and T=1 337 |
从图 3中可以看出,大周期(T=1 337)的周期解与小周期(T=670)的周期解在位置上接近,并且形状类似,因此可以将这组周期解作为倍周期的周期解。
(2) T=1 216和T=2 423。由最速下降方法得到的第二组周期轨道图如图 4所示。

|
图 4 T=1 216和T=2 423时的周期轨道图 Fig.4 The periodic orbits for T=1 216 and T=2 423 |
从图 4中可以看出,大周期(T=2 423)与小周期(T=1 216)的周期解在位置上接近,并且形状相似,因此可以将该组周期解作为倍周期的周期解。
综合以上分析可知,倍周期的存在为周期倍分支的存在提供了依据。
3 结束语本文提出了搜寻混沌系统不稳定周期解的新方法,通过计算机运算得到了130个Lorenz系统的周期解,同时利用该方法为系统找到了非常重要的3种周期解,即朴素周期、超大周期以及倍周期。结果表明本文方法具有较好的实用性和有效性。
| [1] |
BANKS J, BROOKS J, CAIRNS G, et al. On devaney's definition of chaos[J]. The American Mathematical Monthly, 1992, 99(4): 332-334. DOI:10.1080/00029890.1992.11995856 |
| [2] |
丘水生. 混沌吸引子周期轨道理论研究(Ⅱ)[J]. 电路与系统学报, 2004, 9(1): 1-5. QIU S S. Study on periodic orbit theory of chaotic attractors (Ⅱ)[J]. Journal of Circuits and Systems, 2004, 9(1): 1-5. (in Chinese) DOI:10.3969/j.issn.1007-0249.2004.01.001 |
| [3] |
王福来, 达庆利. 广义Lorenz映射的混沌行为及不变密度[J]. 东南大学学报(自然科学版), 2007, 37(4): 711-715. WANG F L, DA Q L. Chaotic behavior of generalized Lorenz maps and its invariant density[J]. Journal of Southeast University (Natural Science Edition), 2007, 37(4): 711-715. (in Chinese) DOI:10.3321/j.issn:1001-0505.2007.04.033 |
| [4] |
穆爱霞. 从有序到无序的混沌实例研究[J]. 牡丹江师范学院学报(自然科学版), 2013, 1(3): 26-27. MU A X. A case study of chaos from order to disorder[J]. Journal of Mudanjiang Normal University, 2013, 1(3): 26-27. (in Chinese) DOI:10.3969/j.issn.1003-6180.2013.03.012 |
| [5] |
MILADI Y, FEKI M, DERBEL N. Stabilizing the unstable periodic orbits of a hybrid chaotic system using optimal control[J]. Commun Nonlinear Sci Numer Simulat, 2015, 20(3): 1043-1056. DOI:10.1016/j.cnsns.2014.06.026 |
| [6] |
潘颖昕, 杜然, 张秀菊. 高次多项式微分系统的周期解[J]. 江南大学学报(自然科学版), 2012, 11(6): 742-746. PAN Y X, DU R, ZHANG X J. Periodic solutions of higher order polynomial differential systems[J]. Journal of Jiangnan University(Natural Science Edition), 2012, 11(6): 742-746. (in Chinese) DOI:10.3969/j.issn.1671-7147.2012.06.023 |
| [7] |
程传蕊. 一种求解非线性方程组的单纯形算法(algorithm)——同伦算法的分析及其收敛性[J]. 长春师范学院学报(自然科学版), 2005, 24(1): 16-18. CHENG C R. One solving nonlinear simple shape algorithm of equation group (algorithm)-with analysis of the human relations algorithm and convergence property[J]. Journal of Changchun Teachers College(Natural Science), 2005, 24(1): 16-18. (in Chinese) DOI:10.3969/j.issn.1008-178X-B.2005.01.007 |
| [8] |
李德信, 徐健学. 求解非线性动力系统周期解推广的打靶法[J]. 应用力学学报, 2003, 20(4): 80-85. LI D X, XU J X. Generalized shooting method for determining the periodic orbit of the nonlinear dynamics system[J]. Chinese Journal of Applied Mechanics, 2003, 20(4): 80-85. (in Chinese) DOI:10.3969/j.issn.1000-4939.2003.04.018 |
| [9] |
王兴元, 骆超. Lorenz系统通向混沌的道路[J]. 大连理工大学学报, 2006, 46(4): 582-587. WANG X Y, LUO C. Approach of Lorenz system to chaos[J]. Journal of Dalian University of Technology, 2006, 46(4): 582-587. (in Chinese) DOI:10.3321/j.issn:1000-8608.2006.04.023 |
| [10] |
李文, 梁昔明. 基于混沌优化和最速下降法的一种混合算法[J]. 计算技术与自动化, 2003, 22(2): 12-14. LI W, LIANG X M. A hybrid algorithm based on chaos optimization and steepest descent algorithm[J]. Computing Technology and Automation, 2003, 22(2): 12-14. (in Chinese) DOI:10.3969/j.issn.1003-6199.2003.02.004 |








