2. 北京化工大学 塑料机械及塑料工程研究所, 北京 100029
2. Institute of Plastic Machinery and Engineering, Beijing University of Chemical Technology, Beijing 100029, China
随着微机械系统的发展以及聚合物微结构制件在生物医学、精密仪表、光纤通信和航空、航天等领域需求的不断增加,微尺度下聚合物的流变特性与成型方法的研究得到广泛关注[1]。研究表明由于尺度效应的影响,微尺度下聚合物的流变特性与常规尺度下不同。微尺度下聚合物的流变特性与材料的结构、剪切速率、流道尺寸、流道表面粗糙度、壁面滑移等因素有关[2-4]。由于微尺度下聚合物的流变实验对实验仪器设备的稳定性、测量精度以及口模流道的加工精度的要求更高,已发表的研究结果不尽相同,甚至相反[5-7]。因此,对于微尺度下聚合物的流变特性需进行更广泛深入的研究。
Maxwell与Jung[8]的研究表明,当压力增加到168MPa时,聚乙烯的黏度增加14倍。后续研究者的研究认为,聚合物熔体的压力增加,减少了聚合物分子间的运动空间,增大了分子运动摩擦力,从而使黏度相应增加[9-10]。常规尺度下,聚合物熔体温度增加使得黏度降低,而压力的增大使黏度提高,聚合物黏度表现为“剪切变稀”。Kelly等[11]指出在高剪切速率下温度与压力对黏度影响的“抵消”关系还需要进一步研究,而在高剪切速率下0.5 mm口模内的流变实验发现聚合物黏度出现“剪切变厚”现象。
Lin等[3]利用毛细管流变仪研究了微尺度下聚甲基丙烯酸甲酯(PMMA)的流变特性,结果表明,温度与压力对PMMA黏度有着重要的影响,压力对黏度的影响系数与温度有关。本课题组前期利用高精度RH10毛细管流变仪研究了微尺度下聚丙烯(PP)的剪切黏度特性[12],研究发现PP的剪切黏度在3个实验温度下显示出明显的口模尺度依赖性:在220、230 ℃时0.25 mm口模内的黏度高于0.5、1.0 mm口模内的黏度,而在210 ℃时3个口模内的黏度值彼此相近;分析结果表明,微尺度下PP熔体压力是黏度产生偏差的原因之一;此外,在210 ℃时0.25 mm口模内PP熔体流动发生壁面滑移。
在前期工作的基础上,本文进一步研究在微小口模内PP熔体剪切黏度、温度、压力与口模尺度之间相互的影响与依赖关系。以体现聚合物黏度与温度关系的Arrhenius公式为依据,进一步验证了微尺度下PP黏度与口模尺度的依赖性关系;基于压力对微小口模内黏度偏差的贡献率提出用于量化微尺度下PP黏度的等效压力的概念。
1 实验部分 1.1 实验原料和仪器 1.1.1 实验原料聚丙烯, R-301,密度0.95 g/cm3,重均分子量430996,分子量分布5.708,韩国晓星公司生产。
1.1.2 实验仪器图 1(a)所示为RH10毛细管流变仪(英国马尔文仪器有限公司)的结构简图。流变仪主要包括料桶(内径15 mm)、推料柱塞、压力传感器及安装在料桶底部作为聚合物熔体流出通道的口模。实验使用两种外径相同而长度不同的口模,即长口模与零口模。长口模的长径比(口模长度与内径之比)为16,零口模的长径比小于1,如图 1(b)所示。口模材料为碳化钨钴合金,以确保在高压作用下口模形状不变。实验前,将实验用材料装满料桶并用工具压实。环绕料桶的加热系统将料桶均匀加热至实验设置温度。材料需要有540 s的预热时间及0.5~1 MPa的预压力,以保证材料受热均匀[11],提高实验结果精度。实验开始时柱塞以与实验设定的剪切速率相匹配的速度向下运动,推动聚合物熔体流出口模。实验过程中熔体的压力由安装在两口模入口处的压力传感器测定。整个实验过程数据可由流变仪自带软件输出。

|
图 1 毛细管流变仪结构与口模 Fig.1 Schematic drawings of the twin-bore capillary rheometer and the dies |
RH10毛细管流变仪所配备最小口模直径为0.25 mm。为较好反映聚合物熔体的流变特性,研究PP熔体在微尺度下(0.25 mm)、常规尺度下(1.0 mm)及其尺度过渡的流变行为,实验选用0.25、0.5和1.0 mm的口模。参考挤出微压印方法制备具有表面微结构的PP光扩散板的实验条件[13],实验设定剪切速率为3×102 ~5×103 s-1,PP熔体温度为210、220、230 ℃,进行重复实验。考虑到长口模入口处压力损失,基于Bagley修正公式,实际口模壁面处的应力为[14]
| ${\tau _{\rm{w}}} = \frac{{R\Delta p}}{{2L}} = \frac{{R({p_{\rm{L}}} - {p_0})}}{{2L}}$ | (1) |
式中,τw为口模壁面处应力,Pa;Δp=pL-p0为口模压力降,pL与p0分别为所测长口模与零口模的压力值,Pa;L与R分别为口模的长度与半径,mm。
对于牛顿流体,根据Poiseulle公式,基于流体流动的体积流量(Q),可计算流体流动的剪切速率(
| ${{\dot \gamma }_{{\rm{app}}}} = \frac{{4Q}}{{{\rm{ \mathsf{ π} }}{R^3}}}$ | (2) |
非牛顿流体流动为柱塞流,其流动前沿不同于牛顿流体的抛物线形状。因此,基于Rabinowitsch修正,非牛顿流体实际流动的剪切速率为[16]
| ${{\dot \gamma }_{{\rm{true}}}} = \left( {\frac{{3n + 1}}{{4n}}} \right){{\dot \gamma }_{{\rm{app}}}}$ | (3) |
| $n = \frac{{{\rm{d}}({\rm{ln}}{\tau _{\rm{w}}})}}{{{\rm{d}}({\rm{ln}}{{\dot \gamma }_{{\rm{app}}}})}}$ | (4) |
式中,Q为流体流动的体积流量,m3/s;
基于公式(1)~(4),流体的表观黏度(ηapp,Pa·s)与实际黏度(ηtrue,Pa·s)为
| ${\eta _{{\rm{app}}}} = \frac{{{\tau _{\rm{w}}}}}{{{{\dot \gamma }_{{\rm{app}}}}}}$ | (5) |
| ${\eta _{{\rm{true}}}} = \frac{{{\tau _{\rm{w}}}}}{{{{\dot \gamma }_{{\rm{true}}}}}}$ | (6) |
以上计算均基于熔体在口模中是轴对称流动,熔体等温且不可压缩假设。同时,熔体在壁面处流动无滑移,即熔体在口模壁面处速度为零。
2 结果与讨论 2.1 口模直径对剪切黏度的影响当T>Tg+100 ℃时,聚合物熔体的黏度对熔体温度的依赖性可用Arrhenius公式表示[17]
| $\eta = A{\rm{exp}}(E_{\rm{r}}^ \cdot /RT)$ | (7) |
式中,η为聚合物熔体的黏度,Pa·s;A为指前因子(也称频率因子);Er·为表观活化能,kJ/mol;R为摩尔气体常量;T为热力学温度,K。
公式(7) 可以改写为
| ${\rm{ln}}\eta = {\rm{ln}}A + \frac{{E_{\rm{r}}^ \cdot }}{R}\frac{1}{T}$ | (8) |
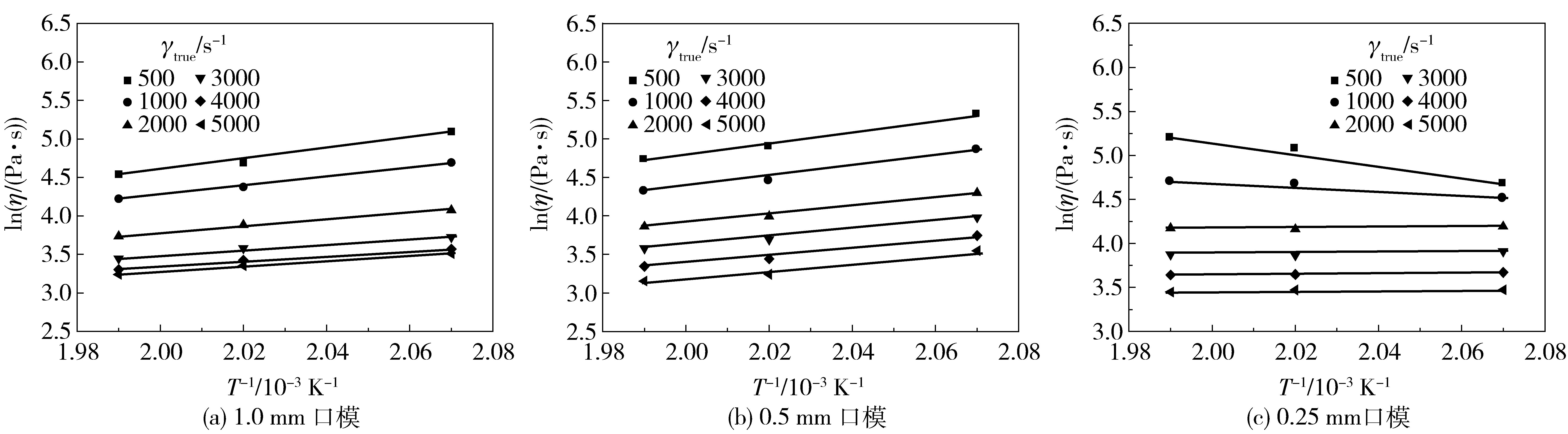
从公式(8) 可以看出,在一定的剪切速率下,lnη与熔体温度的倒数(T-1)存在线性关系。图 2为3种直径口模内,PP熔体温度与剪切黏度的依赖性关系。
|
图 2 不同口模内,PP剪切黏度的lnη与T-1的关系 Fig.2 Relationship between lnη and T-1 for the PP melt with different dies |
图 2显示在不同的剪切速率下,3种不同直径的口模内,PP剪切黏度的lnη与T-1关系曲线近似平行,说明3个口模内熔体黏度与温度之间关系符合Arrhenius公式。然而,从图 2可以看出,3种口模内表示lnη与T-1之间关系的直线斜率不尽相同。表 1为公式(8) 中lnA与Er·/R在3种口模内不同的拟合值,说明PP黏度随温度的变化关系特别是0.25 mm口模内黏度与温度的关系发生了较大的变化。
| 下载CSV 表 1 公式(8) 中lnA与Er·/R在不同口模内的拟合值 Table 1 The fitting values of lnA and Er·/R in equation (8) for different dies |
在1.0 mm的口模中,直线斜率为正,说明随着PP熔体温度的升高,PP的黏度显著降低。在0.5 mm口模内,lnη的值增大,熔体黏度增加,直线斜率有所增加,说明210 ℃时PP在0.5 mm直径口模内的黏度比1.0 mm直径口模的黏度值大。而在0.25 mm直径的口模内,PP黏度的lnη与T-1关系接近水平直线,表明PP黏度随着温度的升高并没有很明显的降低,3个温度下PP熔体的黏度值近似相等。
从图 2还可以看出,在较低的剪切速率下,PP熔体黏度随剪切速率的增加而减小。而当剪切速率达到2000 s-1以后,黏度值降低幅度减小。另外,210 ℃时0.25 mm口模内低剪切速率下黏度受尺度效应影响明显,黏度变化发生偏移,如图 2(c)所示。
表 2为不同实验温度下,当剪切速率为1000、2500、5000 s-1时3种口模内PP的剪切黏度值,以及相同条件下0.25、0.5 mm口模内PP黏度相对于1.0 mm口模内PP的黏度偏差。
| 下载CSV 表 2 相同剪切速率下小口模内PP熔体黏度偏差 Table 2 Deviations of the shear viscosity of the PP melt in a micro die under the same shear rate |
从PP黏度的lnη与T-1关系(图 2)及表 2数据来看,PP熔体的剪切黏度表现出显著的口模尺度依赖性,表明微尺度下尺度效应对PP黏度的影响。相同温度与剪切速率下,PP熔体在不同口模内的黏度不同;随着口模直径的减小,PP熔体的剪切黏度增加。
2.2 微尺度下压力对剪切黏度的影响如2.1节所述,压力的增加减小了聚合物分子间的运动空间,分子间运动的摩擦随之增加,从而影响了聚合物熔体的黏度。图 3为3种温度下,与1.0 mm口模压力相比,0.25、0.5 mm口模内的压力增加值(Δp′,MPa)。

|
图 3 不同温度下0.25,0.5 mm口模内压降的增加 Fig.3 Increase in pressure drop of PP in the 0.25 and 0.5 mm dies under different temperatures |
从0.25、0.5 mm两小口模内的压力变化分析3种实验温度下小口模内黏度产生偏差的原因,可以看出230 ℃时,0.25、0.5 mm口模内PP熔体压力增加的趋势相同,0.25 mm口模内的压力增加显著。在220 ℃时,两口模内的压力增加趋势发生了改变,且压力增加值较230 ℃时降低。当PP熔体温度降至210 ℃时,随着剪切速率的增加,0.25 mm口模内压力增加值增大,但0.5 mm口模内的压力增加值增幅更加明显,大于0.25 mm口模内的压力增加幅度。
以上实验结果表明,3个口模内PP熔体压力的变化不尽相同。常规尺度下,随着剪切速率的增加,温度升高,黏度降低,熔体流动阻力减少,压力增大幅度减小。同时,微尺度下随着口模直径减少,尺度效应增加,口模的熔体压力又有增加的趋势。因此,3个口模内熔体压力的增加是温度与口模尺度综合影响的结果。
聚合物黏度与压力的关系可用Barus公式表示为[18]
| $\eta = {\eta ^{(0)}}{{\rm{e}}^{\beta p}}$ | (9) |
式中,η(0)、η分别为零压力及压力p下聚合物熔体的黏度,Pa·s;β为压力系数,Pa-1。
忽略尺度效应对1.0 mm口模内剪切黏度的影响,视1.0 mm口模内黏度为常规尺度下的PP黏度。基于公式(9) 可以得到小口模内熔体压力的增加对0.25、0.5 mm口模内PP黏度变化的贡献率。
| $\begin{array}{l} \eta _{\rm{m}}^{{\rm{ca}}} = {\eta _{1.0}}{{\rm{e}}^{\beta \Delta p\prime }}\\ \delta = (\eta _{\rm{m}}^{{\rm{ca}}} - {\eta _{1.0}})/{\eta _{1.0}} \end{array}$ | (10) |
式中,δ为小口模内压力增加对黏度变化的贡献率,%;η1.0,ηmca为1.0 mm及0.25/0.5 mm口模的计算黏度,Pa·s;忽略尺度效应对1.0 mm口模黏度的影响,η1.0以1.0 mm口模黏度的实验值计算;Δp′为小口模的压力增量,Δp′=pm-p1.0;p1.0,pm分别为1.0 mm及0.25/0.5 mm口模内的压力,Pa;β为压力系数,Pa-1。
取β为21.5 GPa-1,计算微小口模内压力增加对黏度改变的贡献率[9]。从图 4可以看出,在210及220 ℃时,0.25、0.5 mm两个小口模内压力贡献率随着剪切速率的提高而增加,这与图 3中两个小口模内熔体压力的增加相对应,而在230 ℃时压力的贡献率随着剪切速率的提高而下降。在0.25 mm口模内,压力对黏度的影响作用明显增强。因此,微尺度下PP熔体黏度产生的偏差部分来自于微小口模内熔体压力增加的影响。

|
图 4 不同温度下0.25,0.5 mm口模内压力增加对黏度变化的贡献率 Fig.4 Contribution of the increase in pressure drop to the deviation of the shear viscosity of PP melts in the 0.25 and 0.5 mm dies under different temperatures |
材料的分子结构、剪切速率、流道尺寸、流道的加工精度以及壁面滑移等因素都在不同程度上影响了微尺度下聚合物熔体黏度。微尺度下聚合物熔体黏度的偏差是各因素的相互作用综合影响的结果。而以上微尺度下PP剪切黏度的流变实验结果显示,小口模内PP熔体压力变化是黏度偏差产生的部分原因。
基于公式(9),提出微尺度下口模黏度的等效压力的概念,其意义为除压力影响外,微尺度下其他因素对聚合物剪切黏度的影响,可以等价于一个压力增量,用等效压力pE的影响来表示,以此来量化微尺度下聚合物黏度ηm的变化。
| ${\eta _{\rm{m}}} = {\eta ^{(0)}}{{\rm{e}}^{\beta ({p_{1.0}} + \Delta p\prime + {p_{\rm{E}}}}}) = {\rm{ }}{\eta _{1.0}}{{\rm{e}}^{\beta (\Delta p\prime + {p_{\rm{E}}})}}$ | (11) |
从式(11) 可以看出,量化微尺度下PP熔体黏度的变化可以以常规尺度下PP熔体黏度(η(0))为参考值,如忽略1.0 mm口模的尺度效应,以其黏度值(η1.0)为基值,附加一定压力增量所引起的黏度变化来表示。其中,压力增量是微小口模内熔体压力实际增加值Δp′与等效压力pE之和。除小口模内压力对PP黏度影响外,其他各因素对微小口模黏度的综合影响由等效压力pE的贡献来表示。
3 结论(1) 在微尺度下,由Arrhenius公式表达的lnη与熔体温度倒数(T-1)的线性关系在0.25、0.5 mm口模内发生变化,显示了微尺度下口模尺度对熔体剪切黏度的影响。PP熔体压力随口模直径减小而增加。
(2) 依据Barus公式分析了0.25、0.5 mm口模内的压力增量对剪切黏度变化的贡献率,在此基础上提出了除压力外量化其他各因素对微小口模黏度综合影响的等效压力概念。在某一温度下微小口模内PP黏度值等于常规尺度下的黏度值附加一定压力引起的黏度偏差,此压力是微小口模内压力的增加值与等效压力之和。
| [1] |
Bernassau A L, Garcia-Gancedo L, Hutson D, et al. Microfabrication of electrode patterns for high-frequency ultrasound transducer arrays[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2012, 59(8): 1820-1829. DOI:10.1109/TUFFC.2012.2387 |
| [2] |
Ito H, Suzuki H, Kazama K, et al. Polymer structure and properties in micro-and nanomolding process[J]. Current Applied Physics, 2009, 9(2): e19-e24. DOI:10.1016/j.cap.2008.12.024 |
| [3] |
Lin X, Kelly A, Ren D Y, et al. Geometrical dependence of viscosity of polymethylmethacrylate melt in capillary flow[J]. Journal of Applied Polymer Science, 2013, 130(5): 3384-3394. DOI:10.1002/app.39591 |
| [4] |
Yao D G, Kim B. Simulation of the filling process in micro channels for polymeric materials[J]. Journal of Micromechanics and Microengineering, 2002, 12(5): 604-610. DOI:10.1088/0960-1317/12/5/314 |
| [5] |
Chen S C, Tsai R I, Chien R D, et al. Preliminary study of polymer melt rheological behavior flowing through micro-channels[J]. International Communications in Heat and Mass Transfer, 2005, 32(3): 501-510. |
| [6] |
Azuddin M, Zahari T, Choudhury I A. Observation of polypropylene (PP) melt flow on microchannel using polymethyl methacrylate (PMMA) mold[J]. Materials and Manufacturing Processes, 2011, 26(2): 255-260. DOI:10.1080/10426914.2010.480996 |
| [7] |
Ansari M, Zisis T, Hatzikiriakos S G, et al. Capillary flow of low-density polyethylene[J]. Polymer Engineering & Science, 2012, 52(3): 649-662. |
| [8] |
Maxwell B, Jung A. Hydrostatic pressure effect on polymer melt viscosity[J]. Mod Plast, 1957, 35: 174-182. |
| [9] |
Couch M A, Binding D M. High pressure capillary rheometry of polymeric fluids[J]. Polymer, 2000, 41(16): 6323-6334. DOI:10.1016/S0032-3861(99)00865-4 |
| [10] |
Sedlacek T, Zatloukal M, Filip P, et al. On the effect of pressure on the shear and elongational viscosities of polymer melts[J]. Polymer Engineering & Science, 2004, 44(7): 1328-1337. |
| [11] |
Kelly A L, Gough T, Whiteside B R, et al. High shear strain rate rheometry of polymer melts[J]. Journal of Applied Polymer Science, 2009, 114(2): 864-873. DOI:10.1002/app.v114:2 |
| [12] |
Meng L M, Wu D M, Kelly A, et al. Experimental investigation of the rheological behaviors of polypropylene in a capillary flow[J]. Journal of Applied Polymer Science, 2016, 133(22): 43459. |
| [13] |
王晓伟. 挤出滚压法制备聚合物微结构成型技术的开发与研究[D]. 北京: 北京化工大学, 2011. Wang X W. Development and research on polymer microstructures fabrication technology by extrusion roller embossing process[D]. Beijing:Beijing University of Chemical Technology, 2011. (in Chinese) |
| [14] |
Bagley E B. End corrections in the capillary flow of polyethylene[J]. Journal of Applied Physics, 1957, 28(5): 624-627. DOI:10.1063/1.1722814 |
| [15] |
Malkin A I A, Malkin A Y, Isayev A I. Rheology:concepts, methods, and applications[M]. 2nd ed.. Toronto: ChemTec Publishing: 243-247.
|
| [16] |
Schramm G. A practical approach to rheology and rheometry[M]. Karlsruhe, Germany: Gebrueder HAAKE GmbH, 1994: 229-233.
|
| [17] |
王玉忠, 郑长义. 高聚物流变学导论[M]. 成都: 四川大学出版社, 1993: 167-170. Wang Y Z, Zheng C Y. An introduction to polymer rheology[M]. Chengdu: Sichuan University Press, 1993: 167-170. (in Chinese) |
| [18] |
Barus C. Note on the dependence of viscosity on pressure and temperature[J]. Proceedings of the American Academy of Arts and Sciences, 1891, 27: 13-18. DOI:10.2307/20020462 |








