2. 对外经济贸易大学 金融学院, 北京 100029
2. School of Banking & Finance, University of International Business and Economics, Beijing 100029, China
现代投资组合理论在Markowitz[1]的均值方差模型基础上取得长足发展,但是该模型存在极端假设、高收益惩罚和协方差矩阵复杂等缺陷。后续学者在这一领域展开了深入探究[2-5],相继提出半方差、绝对离差、半绝对离差和VAR等工具以克服均值方差模型的局限性。本课题组对不同风险测度的投资组合模型进行研究,认为不同的风险测度产生的模型效果各异[6]。因此,选取合理的风险测度对于构建高效的投资组合模型无疑起到重要作用。Philippatos等[7]首次利用信息熵度量风险时不依赖收益率分布的性质,建立基于信息熵的投资组合模型。近年来广义熵理论被广泛地应用于金融领域的投资组合中。Huang[2]和Xu等[8]分别运用均值-熵和均值-混合熵探讨了投资组合问题;本课题组将时间序列模糊化,利用信息熵测度建立投资组合模型[9]。本文在可信性理论下以方差和正弦熵作为风险测度指标,引入偏度约束增加正收益概率,从而构建新的投资决策优化模型,并进行实证比较,为寻求高效的投资组合模型研究提供新思路。
1 可信性及正弦熵理论 1.1 可信性理论及其性质定义1 设ξ是可信性空间(Θ, Ρ, Cr)上的模糊变量,并存在有限期望,则其期望E、方差V和偏度S可分别定义为[10]
| $\begin{array}{l} E\left[\xi \right] = \int_0^{ + \infty } {Cr\left\{ {\xi \ge r} \right\}{\rm{d}}r - } \int_{ - \infty }^0 {Cr\left\{ {\xi \le r} \right\}{\rm{d}}r} \\ V\left( \xi \right) = E\left[{{{\left( {\xi- E\left[\xi \right]} \right)}^2}} \right]\\ S\left( \xi \right) = E\left[{{{\left( {\xi- E\left[\xi \right]} \right)}^3}} \right] \end{array}$ |
其中两个积分式中至少有一个是有限的并且满足
| $\begin{array}{l} E\left[{m\xi + n\eta } \right] = mE\left[\xi \right] + nE\left[\eta \right]\\ V\left[{m\xi + n\eta } \right] = {m^2}V\left[\xi \right] + {n^2}V\left[\eta \right]\\ S\left[{m\xi + n\eta } \right] = {m^3}S\left[\xi \right] + {n^3}S\left[\eta \right] \end{array}$ |
其中ξ和η相互独立。
设三角模糊变量ξ=(a, b, c)是可信性空间(Θ, Ρ, Cr)上的一个模糊变量,则易求得其期望、方差及偏度分别为
| $\begin{array}{l} E\left[\xi \right] = \left( {a + 2b + c} \right)/4\\ V\left[\xi \right] = \frac{{33{\alpha ^3} + 21{\alpha ^2}\beta + 11\alpha {\beta ^2} - {\beta ^3}}}{{384\alpha }}\\ S\left[\xi \right] = \frac{{{{\left( {c -a} \right)}^2}\left( {c -2b + a} \right)}}{{32}} \end{array}$ |
其中,α=max{b-a, c-d},β=min{b-a, c-d},a,b,c为实数。
1.2 正弦熵及其性质信息熵只能度量某些变量的不确定性,不适用于所有的不确定性变量,且在衡量变量之间的不确定性程度方面存在缺陷。而正弦熵的表达式中只含有三角模糊变量的上界和下界,可避免复杂计算,更重要的是它还满足次可加性,故本文以适用性更广的正弦熵作为一种不确定性测度—风险测度。
定义2 设ξ是可信性空间(Θ, Ρ, Cr)上的模糊变量,其不确定分布Φ(x)=Cr{ξ≤x},则SE[ξ]=
设ξ是定义在可信性空间(Θ, Ρ, Cr)上的模糊变量,其有不确定分布Φ(x),且
| $\mathit{\Phi }\left( x \right) = Cr\left\{ {\xi \le x} \right\} = \left\{ \begin{array}{l} 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;x \le a\\ \frac{{x-a}}{{2\left( {b-a} \right)}}, \;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;a < x \le b\\ \frac{{x + c-2b}}{{2\left( {c - b} \right)}}, \;\;\;\;\;\;\;\;\;\;{\rm{if}}\;b{\rm{ < }}x \le c\\ 1, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;c < x \end{array} \right.$ |
则ξ的正弦熵的表达式为
| $\begin{array}{l} \;\;\;\;\;\;\;SE\left[\xi \right] = \int_a^b {\sin \left( {\frac{{\pi \left( {x -a} \right)}}{{2\left( {b -a} \right)}}} \right){\rm{d}}x} + \int_b^c {\sin } \\ \left( {\frac{{\pi \left( {x + c -2b} \right)}}{{2\left( {c - b} \right)}}} \right){\rm{d}}x = \frac{\pi }{2}\left( {b - a} \right) + \frac{2}{\pi }\left( {c - b} \right) = \frac{2}{\pi }\left( {c - a} \right) \end{array}$ |
综上定义及性质,设ξi = (ai, bi, ci) (i=1, 2, …, n)是相互独立的三角模糊数,可得组合的期望、方差、偏度、正弦熵的表达式分别为
| $\begin{array}{l} \;\;\;\;E\left[{\sum\limits_{i = 1}^n {{\xi _i}{x_i}} } \right] = \frac{1}{4}\sum\limits_{i = 1}^n {\left( {{a_i} + 2{b_i} + {c_i}} \right){x_i}} \\ \;\;\;\;V\left[{\sum\limits_{i = 1}^n {{\xi _i}{x_i}} } \right] = \\ \sum\limits_{i = 1}^n {x_i^2\left[{\frac{{33\alpha _i^3 + 21\alpha _i^2 + 11{\alpha _i}\beta _i^2-\beta _i^3}}{{384{\alpha _i}}}} \right]} \\ \;\;\;\;S\left[{\sum\limits_{i = 1}^n {{\xi _i}{x_i}} } \right] = \frac{1}{{32}}\sum\limits_{i = 1}^n {x_i^3\left[{{{\left( {{c_i}-{a_i}} \right)}^2}\left( {{c_i}-2{b_i} + {a_i}} \right)} \right]} \\ \;\;\;\;SE\left[{\sum\limits_{i = 1}^n {{\xi _i}{x_i}} } \right] = \frac{2}{\pi }\sum\limits_{i = 1}^n {\left| {{x_i}} \right|\left( {{c_i} -{a_i}} \right)} \end{array}$ |
其中,αi=max{bi-ai, ci-di}, βi=min{bi-ai, ci-di}。
2 基于均值-方差-偏度-正弦熵的投资组合优化模型 2.1 基于马尔科夫方法的模糊收益率预测现有研究表明若将收益率变量设定为随机变量,就意味着证券收益率在未来的变化并不取决于收益率过去的演变轨迹,即满足马尔科夫性[12]。
因此,考虑到证券收益率的模糊性和随机性,本文假设收益率是三角模糊随机变量,采用马尔科夫方法来预测证券日收益率的中心值及左右边界值。首先,统计出证券在样本期内(日)的历史交易数据,包括期初开盘价Rto、期末收盘价Rtc、期间最高价Rth、期间最低价Rtl,其中t=1, 2, …, N,N为样本总数。计算证券各期的收益率rte=(Rtc-Rto)/Rto、最高可能收益率rth=(Rth-Rto)/Rto和最低可能收益率rtl=(Rtl-Rto)/Rto。然后,采用K-means聚类方法将各期收益率的取值范围划分为M个区间,并得到了M个聚类点di,再通过统计的方法计算出收益率取值在某期处于第i区间而下一期处于第j区间的比率Pij=
考虑投资n种风险证券,并假设它们之间相互独立,第i(i=1, 2, …, n)种证券的收益率为模糊变量ξi=(ai, bi, ci),投资比例为xi。以收益率的均值来刻画收益,以收益率的方差和正弦熵度量风险,既考虑了未来收益率的随机不确定性,又兼顾了模糊不确定性,使风险测度指标更加全面、精确和合理。而偏度是衡量各个可能的收益率对期望值偏离的大小,偏度通常越大越好(一般大于0即可),模型目标是最大化收益的同时最小化风险,为此建立多目标投资组合优化模型(Mult-M-V-S-SE)如下。
| $\begin{array}{l} \max E\left[{{\xi _1}{x_1} + {\xi _2}{x_2} + \cdots + {\xi _n}{x_n}} \right]\\ \max V\left[{{\xi _1}{x_1} + {\xi _2}{x_2} + \cdots + {\xi _n}{x_n}} \right]\\ \max S\left[{{\xi _1}{x_1} + {\xi _2}{x_2} + \cdots + {\xi _n}{x_n}} \right]\\ \min SE\left[{{\xi _1}{x_1} + {\xi _2}{x_2} + \cdots + {\xi _n}{x_n}} \right]\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\left\{ \begin{array}{l} \sum\limits_{i = 1}^n {{x_i} = 1} \\ {x_i} \ge 0, i = 1, 2, \cdots, n \end{array} \right. \end{array}$ |
然而,实际投资中,应该考虑投资者行为偏好的不同,需要有针对性地对模型进行调整以满足不同投资者的需求。因为当期望收益低于投资者预期收益水平,而风险高于投资者预期风险水平时,才认为是风险;反之亦然。
设投资者预期收益水平为γ0,预期风险水平为ν0,偏度大于0,γ0和ν0依据投资对风险的厌恶程度决定,为此建立如下单目标投资组合优化模型(M-V-S-SE)
| $\begin{array}{l} \min SE\left[{{\xi _1}{x_1} + {\xi _2}{x_2} + \cdots + {\xi _n}{x_n}} \right]\\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} E\left[{{\xi _1}{x_1} + {\xi _2}{x_2} + \cdots + {\xi _n}{x_n}} \right] \ge {\gamma _0}\\ V\left[{{\xi _1}{x_1} + {\xi _2}{x_2} + \cdots + {\xi _n}{x_n}} \right] \le {\nu _0}\\ S\left[{{\xi _1}{x_1} + {\xi _2}{x_2} + \cdots + {\xi _n}{x_n}} \right] \ge 0\\ \sum\limits_{i = 1}^n {{x_i} = 1} \\ {x_i} \ge 0, i = 1, 2, \cdots, n \end{array} \right. \end{array}$ |
从上海证券交易所选取15只来自于不同板块的股票。考虑到股票市场的时间效应,数据区间的选取不宜太大,故选取了自2014年1月2日至2015年9月14日所有正常开盘时间的日交易数据,并以2014年1月2日至2014年12月31日间的日交易数据样本进行建模,以2015年1月5日至9月14日的日交易数据进行实证,验证模型的有效性和适用性。运用2.1节中的马尔科夫方法预测得到模糊收益率,然后分别求得三角模糊变量的均值、方差、偏度和正弦熵的值,见表 1。
| 下载CSV 表 1 三角模糊收益率及其均值、方差、偏度和正弦熵的值 Table 1 The triangular fuzzy returns and their mean, variance, skewness, and sine entropy |
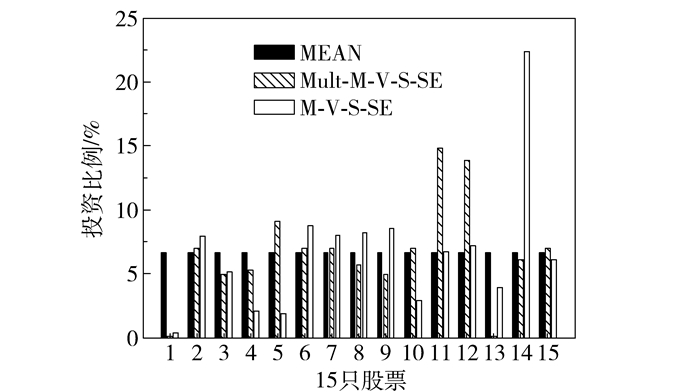
最后,将以上数据代入模型,运用matlab软件中的GA工具箱求解Mult-M-V-S-SE,得到第一组投资比例xi(i=1, 2, …, 15),再根据投资者可接受的预期收益水平和预期风险水平,设定γ0为0.01,ν0为0.007,一般要求偏度大于0即可,求解M-V-S-SE,得到第二组投资比例(i=1, 2, …, 15),并添加均匀投资策略(MEAN)下的投资比例,如图 1。
|
图 1 MEAN、Mult-M-V-S-SE及M-V-S-SE求解结果柱状图 Fig.1 Results of MEAN, Mult-M-V-S-SE and M-V-S-SE models |
经计算,可求得均匀投资策略(MEAN)、Mult-M-V-S-SE及M-V-S-SE的正弦熵的值分别为0.032923、0.031989和0.030693。由图 1可看出,两模型求解的投资比例xi几乎都分布在所有股票中,并没有呈现集中的现象,符合分散投资的理念,并且它们的正弦熵的值接近,说明两模型的求解结果相差无几。但相对而言,单目标模型优于多目标模型,因前者的正弦熵值小于后者,并且单目标模型的灵活性更强,它可以根据不同的投资者的预期来调整收益系数γ0和风险系数ν0,以满足不同的需求,而多目标模型是满足各目标的最优情况,现实中往往难达到。为进一步说明以上两个模型的有效性,接下来进行实证。
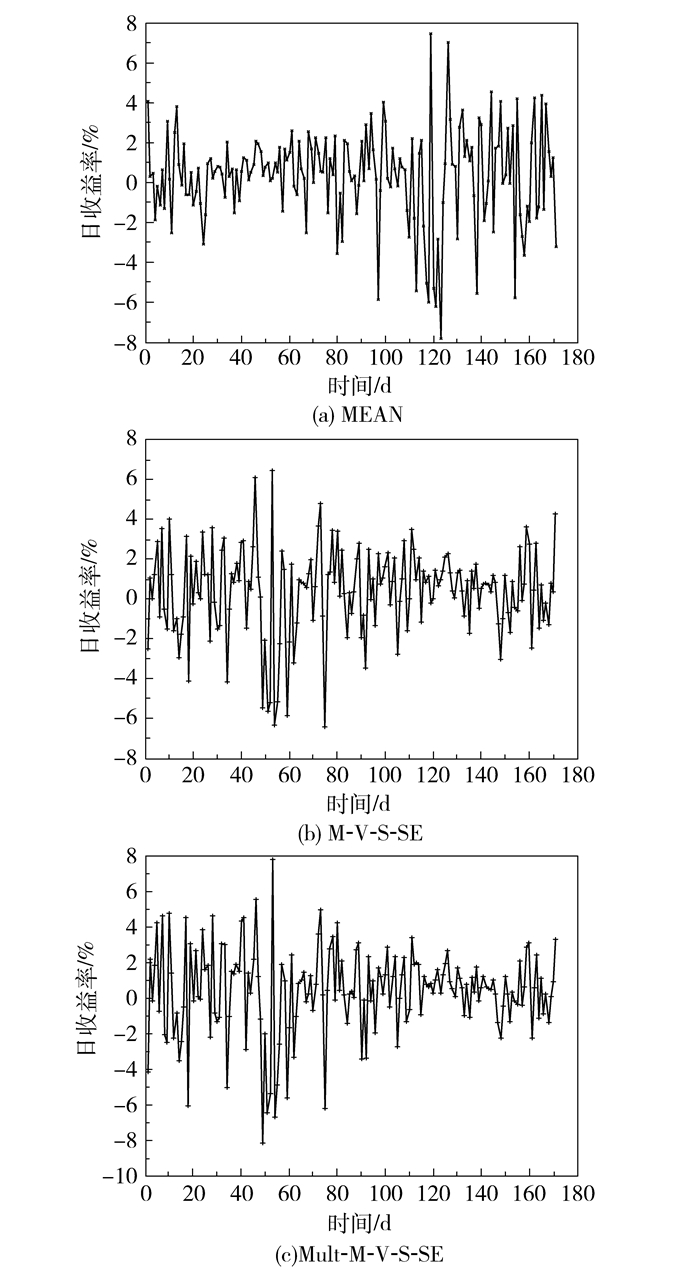
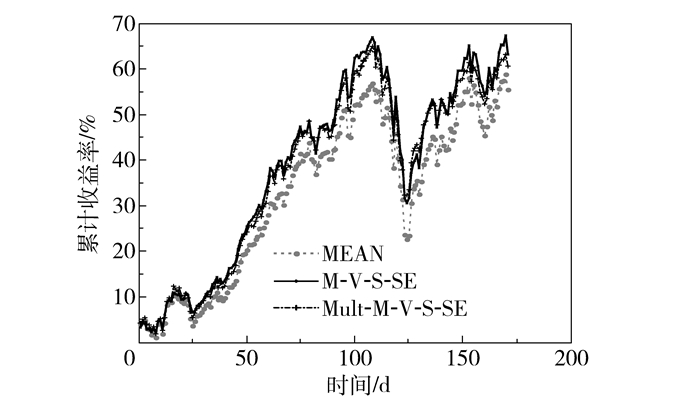
考虑到股票市场中的连续效应,选取2015年1月1日至9月14日的171个交易日数据进行实证研究,得到3种情形下投资组合的日收益率及累计收益率变化图,如图 2和图 3所示。
|
图 2 不同模型的日收益率变化图 Fig.2 The daily rates of the different models |
|
图 3 MEAN、M-V-S-SE和Mult-M-V-S-SE的累积收益率 Fig.3 The cumulative rates of MEAN, M-V-S-SE and Mult-M-V-S-SE models |
由图 2分析可知,3种情形下求得日收益率变化趋势基本相同。但M-V-S-SE的振幅区间为[-6.01%,6.03%],而MEAN和Mult-M-V-S-SE的振幅区间分别为[-8.00%,7.95%]和[-8.56%,7.99%],明显高于M-V-S-SE,说明MEAN和Mult-M-V-S-SE得到的结果波动性较大,稳定性略低,这也和M-VS-SE的正弦熵值略小相吻合。
图 3表明MEAN、Mult-M-V-S-SE以及M-V-S-SE的累积收益率变化走势相似,都是先上升后下降再上升,可能是因为数据区间选取不足造成的。不过M-V-S-SE几乎都在Mult-M-V-S-SE之上,而MEAN表现最差,原因可能是以此样本区间作为研究对象时,投资组合模型中并不适合有多个目标函数。当目标函数过多时,反而使模型的目标不够明确,结果不如M-V-S-SE,加之M-V-S-SE具有更强的可控性,可依据不同类型投资者调整收益,并根据风险系数寻求最符合投资者预期的结果。总体来看,Mult-M-V-S-SE与M-V-S-SE的效果较好,均超过MEAN的累积收益率。若按照两模型计算出来的投资比例进行组合投资,可分别获得高达60.59%和63.23%的收益。另外,若在第一个高点卖掉后,再低位买进,将获得更高的累积收益。
4 结束语本文运用马尔科夫方法预测得到证券的模糊收益率,引入正弦熵作为投资组合的风险测度,建立了多目标和单目标函数投资组合模型,且在单目标模型中,预先设定投资者对于收益、风险水平的预期值,使模型更具灵活性。实证结果表明Mult-M-V-S-SE和M-V-S-SE表现效果较好,都超过均匀投资策略;相对而言,单目标函数模型更具有优势,即在上交所股票短中期投资中运用此策略可获得较高收益。未来可考虑引入交易费用、资金约束及投资者对于低风险和高收益目标中的权衡分配等因素,使模型更加切合真实的金融市场。
| [1] |
Markowitz H. Portfolio selection[J]. Journal of Finance, 1952, 7(1): 77-91. |
| [2] |
Huang X X. Mean-entropy models for fuzzy portfolio selection[J]. IEEE Transactions on Fuzzy Systems, 2008, 16(4): 1096-1101. DOI:10.1109/TFUZZ.2008.924200 |
| [3] |
Brandtner M. Conditional value-at-risk, spectral risk measures and non-diversification in portfolio selection problems-a comparison with mean-variance analysis[J]. Journal of Banking & Finance, 2013, 37(12): 5526-5537. |
| [4] |
Detemple J. Portfolio selection:a review[J]. Journal of Optimization Theory & Applications, 2014, 161: 1-21. |
| [5] |
Dai M, Li P F, Liu H, et al. Portfolio choice with market closure and implications for liquidity premia[J]. Management Science, 2013, 62(2): 368-386. |
| [6] |
余湄, 周荣喜, 吴孟. 投资模型选择问题研究——理论模型及中国股票市场的投资实证研究[J]. 数量经济技术经济研究, 2013(2): 98-110. Yu M, Zhou R X, Wu M. Study on the model selection in portfolio management[J]. The Journal of Quantitative & Technical Economics, 2013(2): 98-110. (in Chinese) |
| [7] |
Philippatos G C, Wilson C J. Entropy, market risk, and the selection of efficient portfolios[J]. Applied Economics, 1972, 4(3): 209-220. DOI:10.1080/00036847200000017 |
| [8] |
Xu J P, Zhou X Y, Wu D D. Portfolio selection using λ mean and hybrid entropy[J]. Annals of Operations Research, 2011, 185(1): 213-229. DOI:10.1007/s10479-009-0550-3 |
| [9] |
Zhou R X, Yang Z B, Yu M, et al. A portfolio optimization model based on information entropy and fuzzy time series[J]. Fuzzy Optimization and Decision Making, 2015, 14(4): 381-397. DOI:10.1007/s10700-015-9206-8 |
| [10] |
Liu B, Liu Y K. Expected value of fuzzy variable and fuzzy expected value models[J]. IEEE Transactions on Fuzzy Systems, 2002, 10(4): 445-450. DOI:10.1109/TFUZZ.2002.800692 |
| [11] |
Kai Y. Sine entropy of uncertain set and its applications[J]. Applied Soft Computing, 2014, 22(5): 432-442. |
| [12] |
Zhou R X, Zhan Y, Cai R, et al. A mean-variance hybrid-entropy model for portfolio selection with fuzzy returns[J]. Entropy, 2015, 17(5): 3319-3331. DOI:10.3390/e17053319 |








