自1987年光子晶体被提出后[1-2],基于其良好的控制光子特性,光子晶体的研究得到了广泛关注。光子晶体具有光子带隙和局域性两大特性,通过在其中引入线缺陷可以形成光子晶体波导。利用光子晶体波导,可以制作调制器[3]、分频器[4]、滤波器[5-8]、偏振器等波导型光学器件,光子晶体波导是光学器件集成化的基本器件之一。Mekis[9]模拟仿真了介质柱放置在空气背景中光子晶体波导的传输行为,结果表明某些频率的光在通过拐角位置时被完全透射,并且通过90°弯曲波导时在一个很大的频率范围内透射率高达95%以上,最高可以达到98%,而相应的普通波导的透射率却只能达到30%。Kim等[10]设计的光子晶体硅波导的直角传输效率达到了99.4%。Mekis等[11]得出了波导模式受波导宽度影响的结论。Xing等[12]通过优化弯曲位置介质柱的结构以及增大半径的方法来提高60°弯曲波导的传输效率。Xiao等[13]通过设计圆形光子晶体的方法来有效降低弯曲波导的传输损耗。Moghadam等[14]通过改变两侧介质柱的半径提高了单模波导的带宽。但这些波导的优化设计主要集中在二维平面内,而Woodpile结构中介电常数沿3个方向作周期性的变化,其波导的优化设计维度更多,可以是平面内的优化设计,也可以是非平面的优化设计。
本课题组前期利用非平面腔腔耦合实现了立体空间输出波导[15]。本文在Woodpile结构中引入Y型波导,利用其三维结构的特点,对Y型波导进行了平面及非平面的优化设计。研究结果表明,这些优化设计都可以有效调节导模的位置,甚至可实现导带向禁带的转换。
1 Y型波导的设计及其透射特性本文设计了工作于微波波段的Woodpile结构,其介质柱尺寸为3 mm×3 mm,晶格常数a=10 mm。介质柱(陶瓷材料Al2O3)和背景材料的相对介电常数(文中简称为介电常数)分别为9.0和1.0,该结构的带隙范围为11.5~14.0 GHz。Woodpile结构中包括3种类型的波导:直接去掉一根完整介质柱形成的X型波导,去掉同一层中每根介质柱的一段形成的Y型波导,沿堆叠方向逐层去掉介质柱的一段形成Z型波导。本文设计了如图 1(a)所示的Y型波导,所设计的Woodpile结构在堆叠方向共4个周期(16层),该波导位于堆叠方向第8层X方向的中间区域, 波导宽度为0.5a。首先利用时域有限差分方法模拟计算了该波导的传输特性。模拟过程中,入射光源为高斯脉冲,放置于波导内,且距离样品边缘1a的位置,偏振方向始终沿着Z方向,即堆叠方向。在波导出射方向,距离波导出口1a的位置设计记录点,用以记录出射光的强度。模拟得到的透射谱如图 1(b)所示。由图可以看出,该波导具有良好的传输特性,其导带的范围为12.26~13.34 GHz,平均透过率接近-3 dB。
在计算模拟中,透过率的计算公式如下
| $T = 10\lg \frac{{{P_{{\rm{in}}}}}}{{{P_{{\rm{out}}}}}}$ |
其中,T代表透过率,单位为分贝(dB);Pin代表光源输入功率;Pout代表波导输出功率。
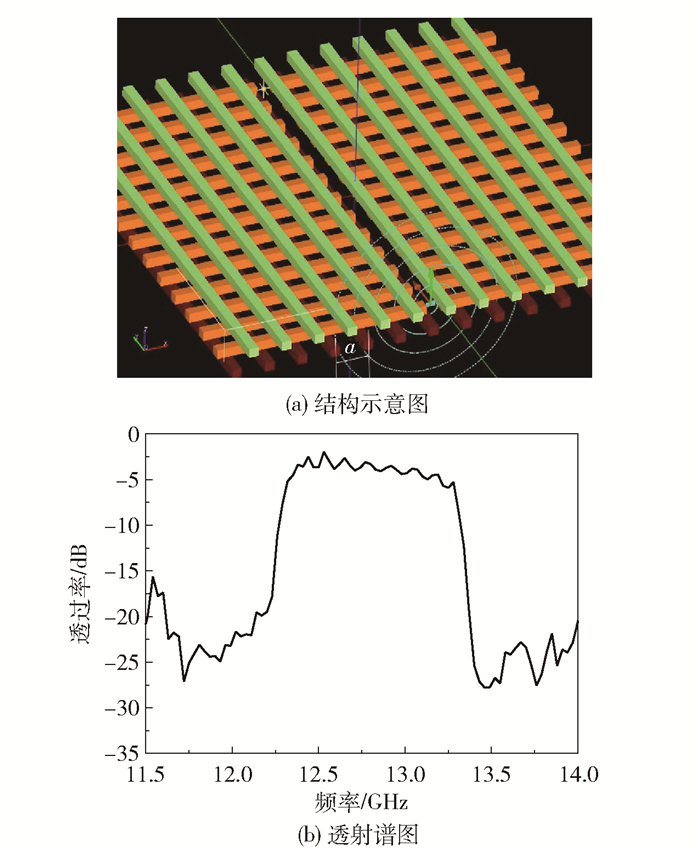
|
图 1 Y型波导结构示意图和透射谱 Fig.1 Schematic diagram and transmission spectrum of the Y-type waveguide |
与二维结构中波导的平面优化设计相比,Woodpile结构中波导的调节可以是平面内的调节,也可以是非平面的调节。首先考虑非平面的调节对波导传输特性的影响。如图 2(a)所示,在波导的右上角(第11层)和左下角(第13层)分别存在两个介质柱,本文就这两个介质柱的位置对波导传输特性的影响进行研究。设定右上角介质柱向左移动为负,向右移动为正;而左下角介质柱向右移动为负,向左移动为正。首先,考虑沿负方向同时移动两个介质柱,且移动距离均为-1 mm时的情况。模拟结果如图 2(b)所示,为了比较,介质柱未移动时的结果也同时给出,图中用黑色的实线表示。可以发现,当两者都移动-1 mm时,导模的范围为12.14~13.25 GHz,导模向低频方向存在微小的移动,且透过率有一定程度的提高。结果说明,Y型波导附近介质柱对波导的传输特性具有重要的影响,它可以有效地调节导模的位置。然后,继续移动两个介质柱,即两者都沿负方向分别移动-2 mm和-3 mm,其透射谱如图 2(c)和(d)所示。比较可以发现,两介质柱沿负方向移动得越多,导模向低频方向平移越明显,导模范围分别为12.10~13.14 GHz和12.02~13.01 GHz。

|
图 2 介质柱移动示意图和介质柱分别移动-1 mm, -2 mm, -3 mm, +1 mm, +2 mm的透射谱 Fig.2 Schematic of the movement of the dielectric cylinder and the transmission spectra for movements of -1 mm, -2 mm, -3 mm, +1 mm, +2 mm |
接着考虑两介质柱向正方向移动时Y型波导的导模变化情况。首先,把两个介质柱同时向正方向移动1 mm,采用时域有限差分方法模拟其透射谱,其结果如图 2(e)所示。此时,出现与沿负方向移动结果完全不同的特性,即移动前后的高带边没有发生变化,但低带边却向高频方向有一个微小的移动。继续向正方向移动两个介质柱,即移动2 mm,其透射谱如图 2(f)所示。可以发现,移动不同距离时,高带边始终保持不变,仅低带边随着移动距离的增加继续向高频方向移动。
2.2 介质柱宽度变化对Y型波导输出特性的调制介质柱位置会影响波导传输特性,介质柱的宽度也会影响波导的传输特性。加宽介质柱的结构如图 3(a)所示,在波导左下角和右上角存在两个介质柱,本文研究了当两个介质柱的宽度同时增加时,对波导的传输特性的影响。首先考虑两个介质柱的宽度增加为4 mm的情况。同样采用时域有限差分方法模拟其透射谱,与原始宽度3 mm的结果(黑实线)进行比较,结果如图 3(b)所示。可以发现,Y型波导的传输特性发生了明显的变化。高带边向低频方向移动,且移动非常明显,而底带边也向低频方向移动,但移动量非常小。此时导模范围为12.14~13.87 GHz。

|
图 3 加宽介质柱示意图和介质柱宽度为4 mm, 5 mm, 6 mm的透射谱 Fig.3 Schematic of changing the dielectric cylinder width and the transmission spectra for widths of 4 mm, 5 mm, 6 mm |
继续增加两介质柱的宽度,分别取5 mm和6 mm,同样模拟了其对应的透射谱,结果如图 3(c)和(d)所示。可以发现,当介质柱宽度增加到5 mm时,初始导带基本变为禁带,而在原禁带位置却出现了一个较窄的导带,其宽度大约为12.02~12.33 GHz。而宽度增加到6 mm时,高频方向出现了一个宽12.92~13.67 GHz的导带,低频方向在原禁带位置出现了一个宽为11.81~11.93 GHz的导带。这些模拟结果说明,改变Y型波导附近介质柱宽度对波导具有很强的调节作用,导带的位置会随着介质柱宽度的变化发生明显的移动,最终导致导带变为禁带的情况。
2.3 介质柱介电常数对Y型波导输出特性的调制除了介质柱的位置和宽度,介电属性也是介质柱的重要结构参数之一。本课题组前期利用材料替换实现了Woodpile结构带隙的调制[16],本文考虑改变波导附近介质柱的相对介电常数,研究波导附近介电常数变化对波导输出特性的影响。如图 4(a)所示,同时改变波导右上角(11层)介质柱a, 左下角(13层)介质柱b的介电常数。首先计算介电常数为8.5的情况下的波导输出特性,结果如图 4(b)所示。为了比较,将介电常数为9.0的结果在图中给出(黑色实线)。可以发现,介电常数微小改变时,Y型波导传输特性基本没有发生变化。继续减小两介质柱的介电常数,即介电常数设置为6.0,模拟结果如图 4(c)所示。比较可以发现,低带边基本保持不变,高带边向高频方向存在一定的移动,即Y型波导的导带范围有一定的增加,其范围为12.29~13.61 GHz。这些结果说明,改变Y型波导附近介质柱的介电常数,可以有效增加导模的范围。

|
图 4 介质柱介电常数同时改变示意图和介电常数为8.5,6.0的透射谱 Fig.4 Schematic of changing the dielectric constant and the transmission spectra for dielectric constants of 8.5, 6.0 |
除了非平面优化方式,三维光子晶体中的波导也可采用平面内优化的方式。与二维光子晶体结构不同的是,在Woodpile结构中的平面内优化不是针对介质柱结构参数的设计,本文主要考虑波导层晶格常数对Y型波导传输特性的影响。首先减小波导层介质柱之间的距离,即相邻介质柱之间的距离取0.9a,其他层的参数不变,该调节Y型波导的宽度不变。同样采用时域有限差分方法模拟其透射谱,结果如图 5(a)所示。可以看出,导模的范围没发生明显的变化,但透过率整体降低。继续增加相邻两柱子之间的距离至1.1a,其透射谱如图 5(b)所示。可以发现,导模存在一定的变化,但变化不明显。这一结果说明,波导层晶格常数的调节对Y型波导的影响相对比较小。

|
图 5 波导所在层晶格常数为0.9a, 1.1a的透射谱 Fig.5 The transmission spectra for 0.9a, 1.1a |
(1) 增加波导上下两侧介质柱的宽度对Y型波导传输特性的影响最为明显,可以获得导带向禁带的转变,且在原禁带的位置会出现一小的导带。
(2) 沿不同方向移动两介质柱对波导传输特性的影响是不同的,沿负方向移动介质柱时,导带向低频方向移动,而沿正方向移动介质柱时,高带边基本保持不变,低带边向高频方向移动。
(3) 改变两介质柱的介电常数和调节波导层介质柱之间的距离对Y型波导的传输特性影响较小。
| [1] |
John S. Strong localization of photons in certain disordered dielectric super lattices[J]. Phys Rev Lett, 1987, 58(23): 2486-2489. DOI:10.1103/PhysRevLett.58.2486 |
| [2] |
Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics[J]. Phys Rev Lett, 1987, 58(20): 2059-2062. DOI:10.1103/PhysRevLett.58.2059 |
| [3] |
Kuramochi E, Notomi M, Huges S, et al. Disorder-induced scattering loss of line-defect waveguides in photonic crystal slabs[J]. Phys Rev B, 2005, 72(16): 161318. DOI:10.1103/PhysRevB.72.161318 |
| [4] |
Sugimoto Y, Ikeda N, Carlsson N, et al. Light-propagation characteristics of Y-branch defect waveguides in AlGaAs-based air-bridge-type two-dimensional photonic crystal slabs[J]. Optic Lett, 2002, 27(6): 388-390. DOI:10.1364/OL.27.000388 |
| [5] |
Noda S, Chutinan A, Imada M. Trapping and emission of photons by a single defect in a photonic bandgap structure[J]. Nature, 2000, 407(6804): 608-610. DOI:10.1038/35036532 |
| [6] |
Fan S, Villeneuve P R, Joannopoulos J D. Channel drop tunneling through localized states[J]. Phys Rev Lett, 1998, 80(5): 960-963. DOI:10.1103/PhysRevLett.80.960 |
| [7] |
Kim S, Park I, Lim H, et al. Highly efficient photonic crystal-based multichannel drop filters of three-port system with reflection feedback[J]. Opt Express, 2004, 12(22): 5518-5525. DOI:10.1364/OPEX.12.005518 |
| [8] |
Qiang Z, Zhou W, Soref R A. Optical add-drop filters based on photonic crystal ring resonators[J]. Opt Express, 2007, 15(4): 1823-1831. DOI:10.1364/OE.15.001823 |
| [9] |
Mekis A. High transmission through sharp bends in photonic crystal waveguides[J]. Phys Rev Lett, 1996, 77(18): 3787-3790. DOI:10.1103/PhysRevLett.77.3787 |
| [10] |
Kim S, Nordin G P, Jiang J H, et al. High efficiency 90° silica waveguide bend using an air hole photonic crystal region[J]. IEEE Photonic Tech L, 2004, 16(8): 1846-1848. DOI:10.1109/LPT.2004.829758 |
| [11] |
Mekis A, Fan S H, Joannopoulos J D. Bound states in photonic crystal waveguides and waveguide bends[J]. Phys Rev B, 1998, 58(8): 4809-4817. DOI:10.1103/PhysRevB.58.4809 |
| [12] |
Xing P F, Borel P I, Frandsen L H, et al. Optimization of bandwidth in 60° photonic crystal waveguide bends[J]. Opt Commun, 2005, 248(1): 179-184. |
| [13] |
Xiao S S, Qiu M. Study of transmission properties for waveguide bends by use of circular photonic crystal[J]. Phys Lett A, 2005, 340(5): 474-479. |
| [14] |
Moghadam K M, Mirsaleh M M, Attari A R. Design of a novel wideband single-mode waveguide in a photonic crystal slab structure[J]. Photonic Nanostruct, 2008, 6(2): 142-147. DOI:10.1016/j.photonics.2008.05.001 |
| [15] |
邵川钋, 冯志芳. Woodpile结构中立体空间波导的研究[J]. 北京化工大学学报:自然科学版, 2015, 42(4): 124-128. Shao C P, Feng Z F. Investigation of a three-dimensional space waveguide with a Woodpile structure[J]. Journal of Beijing University of Chemical Technology:Natural Science, 2015, 42(4): 124-128. (in Chinese) |
| [16] |
冯志芳, 张丹丹. Woodpile结构中带隙的调制[J]. 北京化工大学学报:自然科学版, 2012, 39(2): 110-113. Feng Z F, Zhang D D. Modulation of the band gap in the Woodpile structure[J]. Journal of Beijing University of Chemical Technology:Natural Science, 2012, 39(2): 110-113. (in Chinese) |








