2. 北京化工大学 化工安全教育部工程研究中心, 北京 100029
2. Engineering Research Center of Chemical Safety Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
大型旋转机械转子系统多由多跨转子串联而成,例如在汽轮发电机组中,有高、中、低压汽轮机转子,励磁机和发电机转子等。各跨转子在出厂前经严格动平衡后,现场进行串联组装,由于各跨转子不平衡量的耦合作用,运行过程中仍有可能发生强烈振动。目前常采用现场动平衡的方式,对不平衡转子进行动平衡,但需反复启停机,浪费人力、物力[1-2]。大型旋转机械转子普遍为柔性转子,在启停机阶段经过临界转速时容易发生共振现象,危害机组的安全运行,因此需研究抑制多转子轴系系统过临界转速时振动的方法[3-4]。
采用自动平衡技术能有效抑制转子不平衡振动,例如应用在线自动平衡方法能减小磨床砂轮、汽轮机转子等由于磨损、腐蚀造成的不平衡振动[5-7]。目前液压式和电磁式的自动平衡装置平衡能力有限,工作条件易被限制,多应用在磨床等机械加工器械,难以解决多跨转子串联而成的汽轮机组、离心压缩机组的多转子轴系振动问题[8-9]。
采用磁流变阻尼器抑制轴系振动是一种有效的振动控制方法。汪建晓、孟光[8-11]研究了利用磁流变阻尼器增加转子系统刚度的方法,通过改变临界转速以降低原临界转速处的振动,并采用单目标开关控制使转子安全通过临界转速。邢健等[12]搭建单跨转子实验台进行单目标振动控制实验研究,结果表明磁流变阻尼器对单跨转子振动控制效果良好。吴友海[13]在磁悬浮轴承转子系统中增加磁流变阻尼器,有效抑制了磁悬浮轴承转子振动。刘苑辉[14]设计了带鼠笼结构的剪切式磁流变阻尼器,并应用在单跨转子分析系统中,起到了调节单跨转子振动幅度和频率的效果。
上述研究中只分析了基于磁流变阻尼器的单跨转子抑振效果,对于多跨转子轴系过临界转速各转子间耦合振动的问题,尚无多目标靶向抑制研究。因此,本文针对四跨转子轴系过临界转速易发生各跨转子之间耦合振动的问题,设计了一种转子磁流变阻尼器,搭建了四跨转子实验台,实验了通入磁流变阻尼器电流大小对振动控制的影响;并自主开发了一套基于Labview的四跨转子轴系振动闭环控制系统,以实现多目标在线抑制四跨转子系统过临界转速时的振动。
1 磁流变阻尼器的控制原理与结构 1.1 控制原理磁流变液是一种由非导磁性载液与微米级磁性颗粒混合而成的智能材料[15-16]。在磁场中,磁流变液可在瞬间(毫秒级)由牛顿流体转变为Bingham半固体,且这种转变是可控、可逆和连续的,其效果随磁场增强而提高,直至饱和;转变后的半固体剪切屈服强度与磁场强度有对应关系,使其具有良好的可控性[17]。利用磁流变液制作的磁流变阻尼器具有阻尼可调范围宽、响应迅速、稳定性好、易在线控制等特点[18]。
选用Bingham模型描述阻尼器的力学关系:
| ${F_{\text{m}}}\left( {I, t} \right) = S\eta u\left( t \right)/h + S{\tau _y}\left( I \right)$ | (1) |
式中,Fm(I, t)表示阻尼力,S为磁效面积,η为磁流变液黏度,I为电流,h为阻尼片间隙,τy为磁流变液屈服应力。表 1为磁流变阻尼器电流与磁场强度的对应关系[19]。
| 下载CSV 表 1 磁场强度与电流对应关系 Table 1 Correspondence between the current and the magnetic field strength |
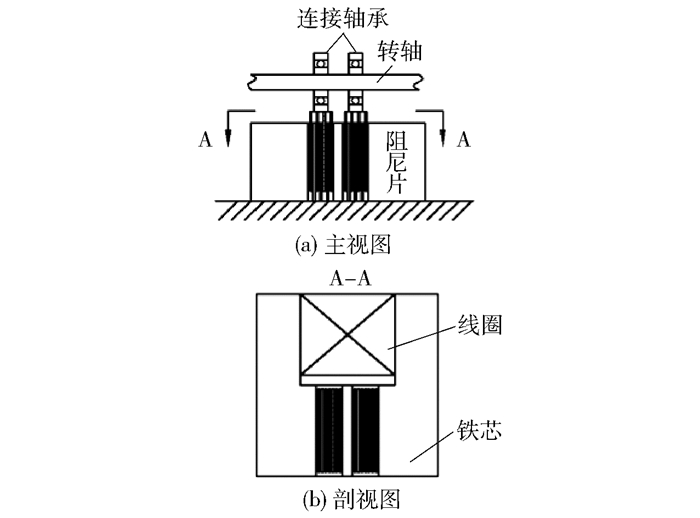
图 1、2为磁流变阻尼器结构示意图和实物图。阻尼器由两个连接轴承、阻尼片、线圈、铁芯和磁流变液组成。铁芯与实验台基座固定,阻尼片分别与两个连接轴承和实验台基座连接,上下交叉排列,阻尼片之间有一定间隙。
|
图 1 磁流变阻尼器示意图 Fig.1 Schematic of the magnetorheological damper |

|
图 2 磁流变阻尼器实物图 Fig.2 Photograph of the magnetorheological damper |
在应用磁流变阻尼进行四跨转子轴系振动抑制的研究中,先理论分析磁流变阻尼对转子动力特性的影响,再利用Dyrobes软件建立有限元模型,仿真分析磁流变阻尼的抑振效果。
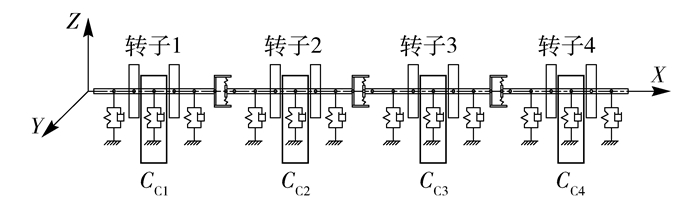
2.1 动力学分析首先,根据多转子轴系动力学相似性、结构相似性和计算方法适应性的特点,建立四跨转子轴系动力学模型,对转轴、圆盘、联轴器、轴承座、支承等结构部件进行动力学模型化。四跨转子轴系结构中各转子通过支承、联轴器组成复杂的动力耦合系统,用弹簧单元和阻尼单元表示支承和联轴器处约束,在各跨转子中间用阻尼单元表示磁流变阻尼,如图 3所示。
|
图 3 多转子轴系集总参数模型 Fig.3 Lumped parameter model of the multi-span shaft system |
然后,对四跨转子-支承-联轴器-磁流变阻尼系统各部件进行受力分析,其动力学方程为:
| $\mathit{\boldsymbol{M\ddot Z}} + \left( {\mathit{\boldsymbol{C}} + {\mathit{\boldsymbol{C}}_{\rm{c}}}} \right)\mathit{\boldsymbol{\dot Z}} + \mathit{\boldsymbol{KZ}} = \mathit{\boldsymbol{F}}\left( t \right)$ | (2) |
其中,位移向量Z为转子系统各结点处自由度,可表示为Z={xj, yj, -θxj, θyj}。
下列各式下角标中r表示转动,p表示平动,e表示单元。M为转子系统离散化质量矩阵,可表示为
| $\left\{ \begin{gathered} \mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}_{\rm{r}}} + {\mathit{\boldsymbol{M}}_{\rm{p}}} \hfill \\ {\mathit{\boldsymbol{M}}_{\rm{r}}} = \sum {{\mathit{\boldsymbol{M}}_{{\rm{er}}}}} \hfill \\ {\mathit{\boldsymbol{M}}_{\rm{p}}} = \sum {{\mathit{\boldsymbol{M}}_{{\rm{ep}}}}} \hfill \\ \end{gathered} \right.$ | (3) |
K为转子系统的刚度矩阵,可表示为
| $\left\{ \begin{gathered} \mathit{\boldsymbol{K}} = {\mathit{\boldsymbol{K}}_{\rm{r}}} + {\mathit{\boldsymbol{K}}_{\rm{p}}} \hfill \\ {\mathit{\boldsymbol{K}}_{\rm{r}}} = \sum {{\mathit{\boldsymbol{K}}_{{\rm{er}}}}} \hfill \\ {\mathit{\boldsymbol{K}}_{\rm{p}}} = \sum {{\mathit{\boldsymbol{K}}_{{\rm{ep}}}}} \hfill \\ \end{gathered} \right.$ | (4) |
Cc、C为转子系统的磁流变阻尼矩阵和其余阻尼项矩阵。在选取转子阻尼模型时,采用广泛应用的经典Rayleigh阻尼模型。该模型可以将阻尼矩阵转化为刚度矩阵和质量矩阵的线性组合,即
| $\mathit{\boldsymbol{C}} = \alpha \mathit{\boldsymbol{M}}{\rm{ + }}\beta \mathit{\boldsymbol{K}}$ | (5) |
其中线性系数α和β可由下式求得
| $\left\{ \begin{gathered} \alpha \hfill \\ \beta \hfill \\ \end{gathered} \right\} = 2\frac{{{\omega _1}{\omega _2}}}{{\omega _2^2- \omega _1^2}}\left[{\begin{array}{*{20}{c}} {{\omega _2}}&{-{\omega _1}} \\ {\frac{{-1}}{{{\omega _2}}}}&{\frac{{-1}}{{{\omega _1}}}} \end{array}} \right]\left\{ \begin{gathered} {\xi _1} \hfill \\ {\xi _2} \hfill \\ \end{gathered} \right\}$ | (6) |
式中,ω1、ω2分别为转子系统的第一、二阶固有频率;ξ1、ξ2分别为第一、二阶模态的阻尼比,可由实验决定。因此磁流变阻尼矩阵Cc可表示为
| $\left\{ \begin{gathered} {\mathit{\boldsymbol{C}}_{\rm{c}}} = {\mathit{\boldsymbol{C}}_{{\rm{cr}}}} + {\mathit{\boldsymbol{C}}_{{\rm{cp}}}} \hfill \\ {\mathit{\boldsymbol{C}}_{{\rm{cr}}}} = \alpha {\mathit{\boldsymbol{M}}_{{\rm{cr}}}} + \beta {\mathit{\boldsymbol{K}}_{{\rm{cr}}}} \hfill \\ {\mathit{\boldsymbol{C}}_{{\rm{cp}}}} = \alpha {\mathit{\boldsymbol{M}}_{{\rm{cp}}}} + \beta {\mathit{\boldsymbol{K}}_{{\rm{ep}}}} \hfill \\ \end{gathered} \right.$ | (7) |
其余阻尼项矩阵C可表示为
| $\left\{ \begin{array}{l} \mathit{\boldsymbol{C}} = {\mathit{\boldsymbol{C}}_{\rm{r}}} + {\mathit{\boldsymbol{C}}_{\rm{p}}}\\ {\mathit{\boldsymbol{C}}_{\rm{r}}} = \alpha {\mathit{\boldsymbol{M}}_{\rm{r}}} + \beta {\mathit{\boldsymbol{K}}_{\rm{r}}}\\ {\mathit{\boldsymbol{C}}_{\rm{p}}} = \alpha {\mathit{\boldsymbol{M}}_{\rm{p}}} + \beta {\mathit{\boldsymbol{K}}_{\rm{p}}} \end{array} \right.$ | (8) |
F(t)为转子系统各部件所受到的激振力合力,转子在陀螺效应的作用下,转子系统方程则变为:
| $\begin{array}{l} \;\;\;\mathit{\boldsymbol{M\ddot Z}} + \left( {\mathit{\boldsymbol{C}} + {\mathit{\boldsymbol{C}}_{\rm{c}}}} \right)\mathit{\boldsymbol{\dot Z}} + \mathit{\boldsymbol{KZ}} = \mathit{\boldsymbol{G}} + \mathit{\boldsymbol{Q}}\left( t \right) + {\mathit{\boldsymbol{F}}_{\rm{C}}} + \mathit{\boldsymbol{F}}\left( {z, } \right.\\ \left. {\dot z, \mathit{\Omega }} \right) \end{array}$ | (9) |
式中, G为转子系统的重力,Q(t)为转子系统的不平衡力,FC为联轴器作用力,
式(9) 为四跨转子-支承-联轴器-磁流变阻尼系统动力学方程,该方程右端的联轴器作用力和非线性油膜力是非线性项,因此该方程为非线性多自由度动力学方程,可利用Dyrobes有限元软件进行数值仿真求解。
2.2 振动控制仿真计算根据工程实际工况与实验台条件,运用Dyrobes有限元软件进行建模分析和仿真计算。建立四跨转子轴系无阻尼和有阻尼模型,如图 4所示。

|
图 4 四跨转子轴系模型 Fig.4 Finite element model of the four-span rotors |
模型中转子轴径为15 mm,转盘外径为200 mm,质量为6.89 kg,轴1、2、3、4跨距长度分别为480、600、735、725 mm。各支撑的刚度为1×104 N/mm,联轴器径向刚度Kt为100 N/mm,旋转刚度Kr为1×105 N·mm。蔡永飞[20]研究磁流变阻尼对转子的影响,发现阻尼值取700 N·s/m左右时对转子抑振效果最好,因此本文模型中取磁流变阻尼值为700 N·s/m。
仿真计算中,先计算四跨转子轴系各阶临界振型及临界转速值,模拟轴系过临界转速时各跨转子振动情况;再进行磁流变阻尼抑振仿真计算,研究磁流变阻尼对轴系过临界转速振动的抑振效果。
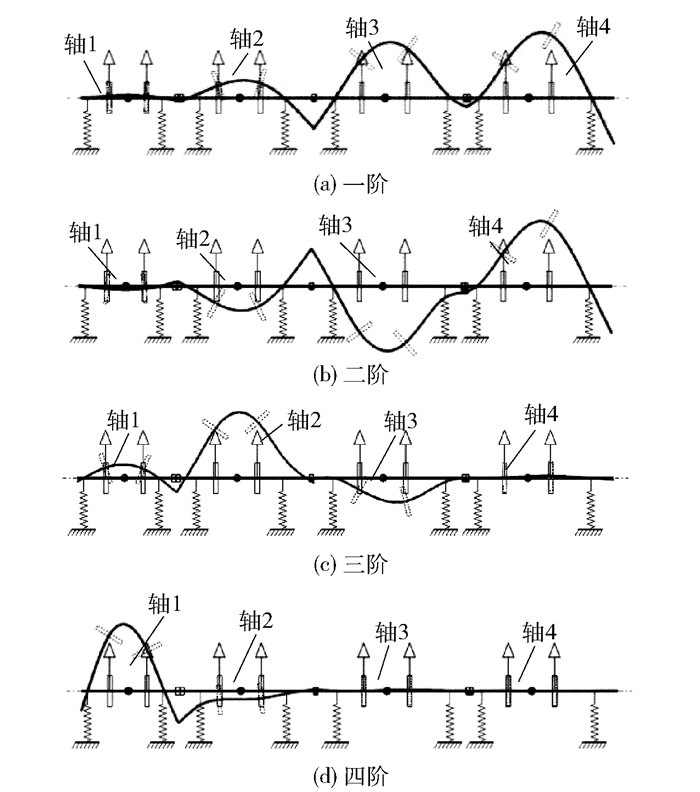
首先计算四跨转子轴系的前四阶临界转速振型如图 5所示。
|
图 5 四跨转子轴系各阶振型 Fig.5 Vibration mode of the four-span rotors |
可以看出,由于轴3、轴4临界转速接近,计算得到转子轴系的一阶、二阶临界转速分别为998、1050 r/min,轴3、轴4振动比较显著,如图 5(a)、(b)所示;计算得到转子轴系的三阶临界转速为1327 r/min,轴2振动比较显著如图 5(c)所示;计算得到转子轴系的四阶临界转速为1763 r/min,轴1振动比较显著,如图 5(d)所示。
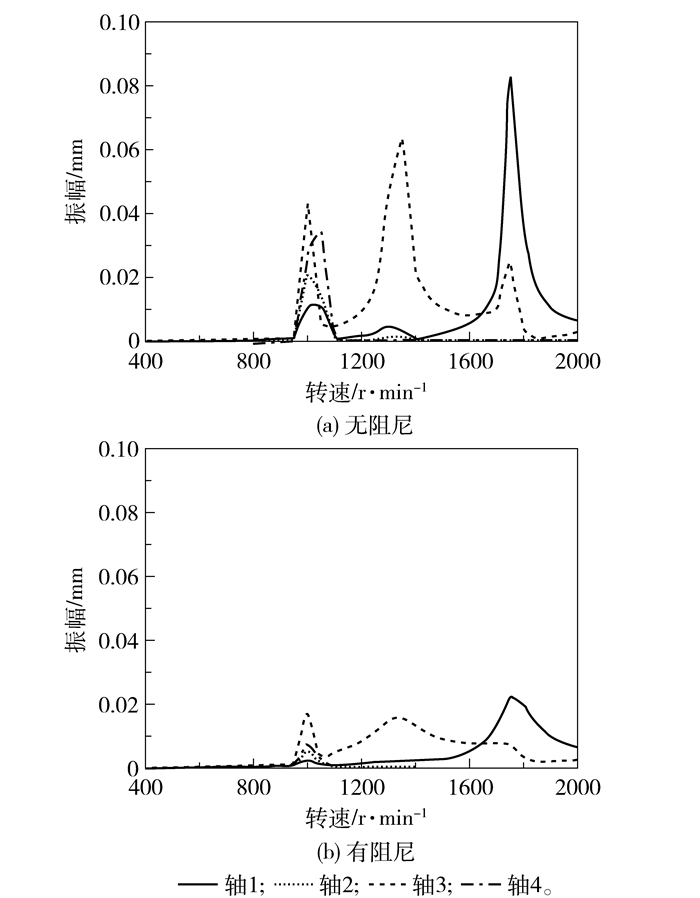
然后在无阻尼和有阻尼模型的对比工况下,分别对四跨转子轴系进行0~2000 r/min的升速实验仿真计算。计算完毕后,提取两种工况下各跨转子左侧支撑处的振动响应,得到振动响应图如图 6所示。
|
图 6 不同工况下轴系各轴支撑处振动响应 Fig.6 Vibration response of the multi-span rotors |
对比图 6仿真计算结果可知,磁流变阻尼能有效抑制四跨转子过临界转速时的振动,其中降幅最大达77.8%,使升速过程中轴系运行平稳。
3 四跨轴子轴系磁流变阻尼器减振实验根据磁流变阻尼器的结构特性与抑振仿真计算结果,搭建四跨转子轴系实验台开展实验验证,研究磁流变阻尼器的抑振特性与效果。
3.1 实验台参数四跨转子轴系磁流变阻尼器减振实验台如图 7所示。该轴系中包括驱动皮带、四跨双盘转子和3个弹性联轴器。各跨转子均为双支撑,阻尼器安装在各跨转子的中间,轴系参数如表 2所示。实验测试用硬件系统包括LC-8000多通道振动采集系统、4个NI9263同步更新模拟输出模块和4个可调电源。测量支撑摆架水平方向振动加速度。

|
图 7 四跨转子轴系实验台 Fig.7 View of the four-span rotor bench |
| 下载CSV 表 2 四跨转子轴系基本参数 Table 2 Parameters of the four-span rotors |
根据原始振动数据与仿真所得的四跨转子轴系耦合振动规律,使用开关控制策略进行多目标靶向在线抑振实验。实验过程中,先测得各跨转子无磁流变阻尼器时原始振动数据,再测量通入磁流变阻尼器电流大小不同时的抑振效果,确定合适的电流大小。
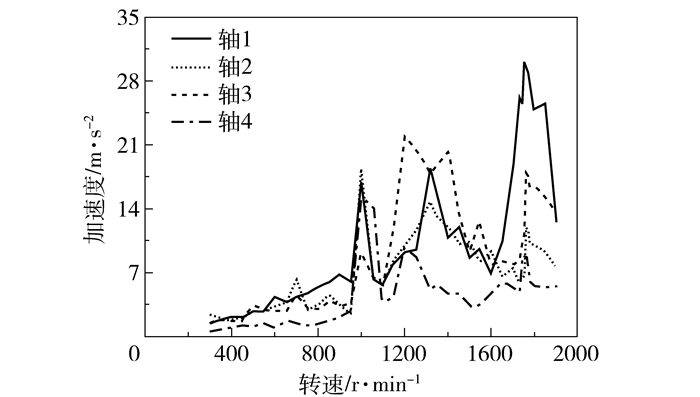
3.2.1 原始振动四跨转子轴系匀速上升到1900 r/min,实验测得轴系原始振动数据如图 8所示。测量各测点的振动数据可得,轴1的临界转速约为1800 r/min,轴2的临界转速约为1300 r/min,轴3、4的临界转速值约为1000 r/min,与仿真计算结果基本相符。
|
图 8 四跨转子轴系原始振动 Fig.8 Origin vibration of the four-span rotors |
升速过程中,当轴系转速在轴系的一阶、二阶临界共振区1000 r/min左右时,轴3、4振动剧烈(最高幅值分别为18.4 m/s2、15.1 m/s2),引起轴1振动(最高幅值为16.7 m/s2);当轴系转速在轴系的三阶临界共振区1300 r/min左右时,轴2振动剧烈(最高幅值为17.9 m/s2),引起轴1、3振动(最高幅值分别为18.4 m/s2、14.8 m/s2);当轴系转速在轴系的四阶临界共振区1800 r/min左右时,轴1振动剧烈(最高幅值为30.1 m/s2),引起轴2、3振动(最高幅值分别为17.8 m/s2、11.8 m/s2)。
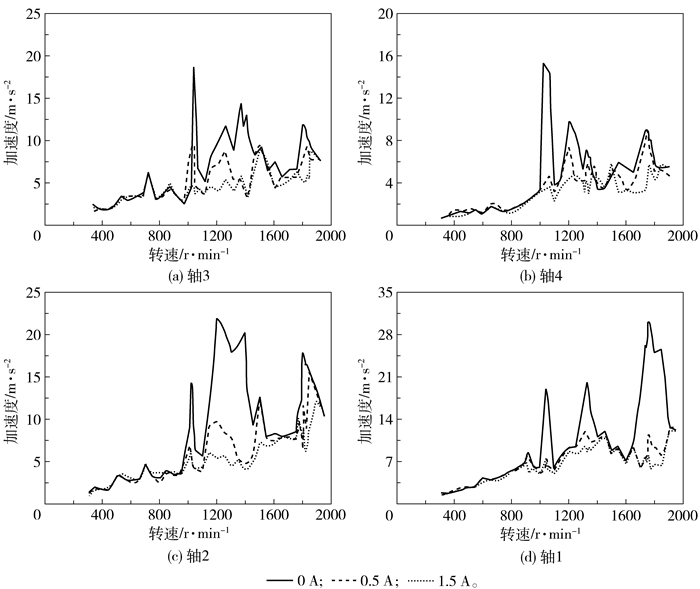
3.2.2 不同电流对阻尼器性能的影响为了研究通入不同大小电流时磁流变阻尼器的抑振效果,在原始振动数据的基础上,4个阻尼器全程分别通入0.5 A、1.5 A电流以观察各跨转子的抑振规律,实验结果见图 9。如图 9(a)、(b)所示,通入电流1.5 A,当轴系转速在临界转速1000 r/min左右时,轴3最大振幅从18.7 m/s2降到8.6 m/s2,降幅达54.01%,轴4最大振幅从15.3 m/s2降到3.3 m/s2,降幅达78.4%,同时轴1、2振幅均有减小;如图 9(c)所示,当轴系转速在临界转速1300 r/min左右时,轴2最大振幅从21.9 m/s2降到5.3 m/s2,降幅达75.8%,同时轴1、3振幅均有减小;如图 9(d)所示,当轴系转速在临界转速1800 r/min左右时,轴1最大振幅从30.1 m/s2降到9.4 m/s2,降幅达68.8%,同时轴2、3振幅均有减小。由此可见,通入电流比不通入电流时振幅有不同程度下降,且电流越大,磁流变阻尼器的性能越好,在通入1.5 A电流时,轴系振动明显下降到较低水平。即通入电流大小对抑制振动有明显影响,与上述的仿真计算结果基本相符。
|
图 9 不同电流下各跨转子振动数据 Fig.9 Vibration data with different currents applied to each rotor |
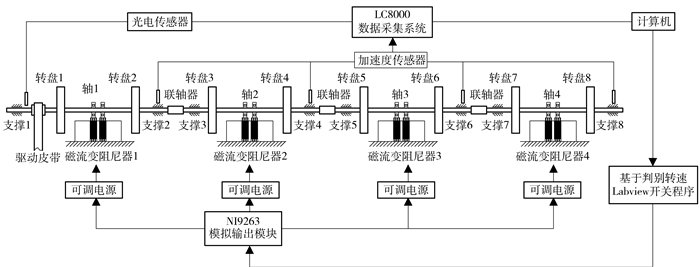
由仿真计算结果和原始振动数据可知,四跨转子轴系过临界转速时耦合振动剧烈,各跨转子带动相邻转子产生较大振动。因此本文提出基于转速的多目标靶向在线开关控制方法,采用靶向开关控制,分别在线控制4个阻尼器的工作时间,实现靶向抑振目标。控制系统工作原理如图 10所示。转速和加速度分别由光电传感器和加速度传感器测得,通过LC8000数据采集系统将测得信号传输到计算机;应用Labview程序进行转速判别,并将控制信号传递到NI9263同步更新模拟输出模块;NI9263输出模块依据控制信号靶向控制各磁流变阻尼器对应连接的可调电源,从而控制4个阻尼器的开关。根据图 8所示的各跨转子临界共振区间,确定阻尼器1的工作区间为1600~1850 r/min,阻尼器2的工作区间为1150~1500 r/min,阻尼器3、4的工作区间为950~1100 r/min。
|
图 10 四跨转子轴系控制系统原理图 Fig.10 Schematic diagram of the control system for the four-span rotors |
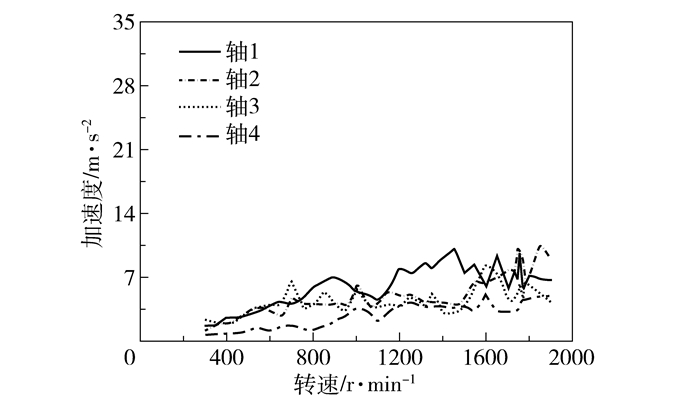
实验控制过程及效果如下:当轴系转速匀速上升到950 r/min时,阻尼器3、4通入电流(1.5 A),转子轴系一阶、二阶临界共振区的振动得到有效抑制,轴1、3、4振幅分别降至7.1、5.5、3.8 m/s2,轴3、4最大降幅分别为68.5%、74.8%,当轴系转速达到1100 r/min时阻尼器3、4电流断开;当轴系转速达到1150 r/min时,阻尼器2通电(1.5 A),转子轴系三阶临界共振区的振动得到有效抑制,轴1、2、3的振幅分别降至8.6、4.1、3.6 m/s2,轴2最大降幅为77.1%,当轴系转速达到1500 r/min时阻尼器2电流断开;当轴系转速达到1600 r/min时,阻尼器1通电(1.5 A),转子轴系四阶临界共振区的振动得到有效抑制,轴1、2、3的振幅分别降至7.2、10.5、6.6 m/s2,轴1最大降幅达76.1%,轴系转速为1850 r/min时断电。轴系振动情况如图 11所示,四跨转子轴系在升速过程中振动较小,运行平稳。因此,使用多目标靶向开关控制方法,能实现靶向抑制四跨转子振动,且大幅减小了各跨转子之间的耦合振动影响。
|
图 11 四跨转子开关控制时的振动情况 Fig.11 Plot of vibration with on-off control of the four-span rotors |
(1) 根据磁流变阻尼器的减振原理,利用有限元仿真软件验证了磁流变阻尼的有效性,最大振动降幅达77.8%,为开展实验提供了理论基础。
(2) 不同电流大小对磁流变阻尼器性能有显著影响,电流越大,抑振效果越好,通入阻尼器中电流为1.5 A时,轴系过临界转速振动降幅最大达78.4%,轴系运行平稳,与理论计算结果相吻合。
(3) 采用在轴系中各跨转子临界转速附近开启、非临界转速关闭的方法控制4个磁流变阻尼器的工作时间,可以大幅减小四跨转子之间的耦合振动影响,轴系过各阶临界转速时振动降幅最大达77.1%,实现了在线多目标靶向抑制多转子轴系过临界转速时的振动。
| [1] |
高金吉, 缪红燕, 徐鸿, 等. 多转子轴系优化耦联及其不平衡响应有限元分析[J]. 振动与冲击, 2005, 24(2): 1-4. Gao J J, Miao H Y, Xu H, et al. Multi-rotors system coupling optimization and unbalance response analysis with finite element method[J]. Journal of Vibration and Shock, 2005, 24(2): 1-4. (in Chinese) |
| [2] |
Zhou J, Di L, Cheng C L, et al. A rotor unbalance response based approach to the identification of the closed-loop stiffness and damping coefficients of active magnetic bearings[J]. Mechanical Systems and Signal Processing, 2016, 66/67: 665-678. DOI:10.1016/j.ymssp.2015.06.008 |
| [3] |
Das A S, Dutt J K, Ray K. Active vibration control of unbalanced flexible rotor-shaft systems parametrically excited due to base motion[J]. Applied Mathematical Modelling, 2010, 34(9): 2353-2369. DOI:10.1016/j.apm.2009.11.002 |
| [4] |
蒋科坚, 祝长生. 基于在线识别对转速不敏感的主动电磁轴承转子系统不平衡振动控制[J]. 中国电机工程学报, 2010, 30(6): 93-99. Jiang K J, Zhu C S. On-line identification based unbalance vibration control with less regard to rotor speed in active magnetic bearings supporting rotor system[J]. Proceedings of the CSEE, 2010, 30(6): 93-99. (in Chinese) |
| [5] |
苏奕儒, 何立东, 汪振威, 等. 单盘刚性转子双平面液压主动平衡技术研究[J]. 中国电机工程学报, 2009, 29(35): 119-124. Su Y R, He L D, Wang Z W, et al. Study on dual-plane active hydraulic balancing technology for single-disk rigid rotor system[J]. Proceedings of the CSEE, 2009, 29(35): 119-124. (in Chinese) DOI:10.3321/j.issn:0258-8013.2009.35.019 |
| [6] |
Zhou S, Shi J. Optimal one-plane active balancing of a rigid rotor during acceleration[J]. Journal of Sound and Vibration, 2002, 249(1): 196-205. DOI:10.1006/jsvi.2001.3660 |
| [7] |
Gosiewski Z. Automatic balancing of flexible rotors.part Ⅱ:synthesis of system[J]. Journal of Sound and Vibration, 1987, 114(1): 103-119. DOI:10.1016/S0022-460X(87)80237-7 |
| [8] |
汪建晓, 孟光. 磁流变液阻尼器用于振动控制的理论及实验研究[J]. 振动与冲击, 2001, 20(2): 41-47. Wang J X, Meng G. Theoretical and experimental study on the vibration control by magnetorheological fluid dampers[J]. Journal of Vibration and Shock, 2001, 20(2): 41-47. (in Chinese) |
| [9] |
汪建晓, 孟光. 磁流变液阻尼器-转子-滑动轴承系统稳定性实验研究[J]. 振动工程学报, 2003, 16(1): 71-74. Wang J X, Meng G. Experimental study on stability of a rotor supported on a MR fluid damper and sliding bearing[J]. Journal of Vibration Engineering, 2003, 16(1): 71-74. (in Chinese) |
| [10] |
汪建晓, 孟光. 磁流变液阻尼器-柔性转子系统振动特性与控制的再研究[J]. 机械强度, 2003, 25(4): 378-383. Wang J X, Meng G. Re-study on vibration performance and control of magnetorheological fluid damper-flexible rotor system[J]. Journal of Mechanical Strength, 2003, 25(4): 378-383. (in Chinese) |
| [11] |
汪建晓, 孟光. 磁流变液阻尼器用于转子振动控制的实验研究[J]. 华中科技大学学报, 2001, 29(7): 47-49. Wang J X, Meng G. Vibration control of rotor by magnetorheological fluid damper[J]. Journal of Huazhong University of Science and Technology, 2001, 29(7): 47-49. (in Chinese) |
| [12] |
邢健, 何立东, 王锎. 基于磁流变液阻尼器的单跨转子振动主动控制实验研究[J]. 仪器仪表学报, 2013, 32(12): 48-54. Xing J, He L D, Wang K. Experimental study of active control techniques for single span rotor vibration[J]. Chinese Journal of Scientific Instrument, 2013, 32(12): 48-54. (in Chinese) |
| [13] |
吴友海. 支承磁悬浮轴承转子系统的磁流变阻尼器研究[D]. 南京: 南京航空航天大学, 2010. Wu Y H. Research on magneto-rheological damper support for magnetic bearing[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2010. (in Chinese) |
| [14] |
刘苑辉. 磁流变阻尼器——转子系统的有限元分析[D]. 广州: 华南理工大学, 2011. Liu Y H. The finite element analysis of magnetorheological damper-rotor system[D]. Guangzhou:South China University of Technology, 2011. (in Chinese) |
| [15] |
宗路航. 磁流变阻尼器的动力学模型及其在车辆悬架中的应用研究[D]. 合肥: 中国科学技术大学, 2013. Zong L H. Magnetorheological dampers:dynamic models and application in vehicle suspensions[D]. Hefei:University of Science and Technology of China, 2013. (in Chinese) |
| [16] |
Ahamed T I, Sundarrajan R, Prasaatha G T, et al. Implementation of magneto-rheological dampers in bumpers of automobiles for reducing impacts during accidents[J]. Procedia Engineering, 2014, 97: 1220-1226. DOI:10.1016/j.proeng.2014.12.400 |
| [17] |
Talatahari S, Rahbari N M. Enriched imperialist competitive algorithm for system identification of magneto-rheological dampers[J]. Mechanical Systems and Signal Processing, 2015, 62: 506-516. |
| [18] |
Chooi W W, Oyadiji S O. Design, modelling and testing of magnetorheological (MR) dampers using analytical flow solutions[J]. Computers and Structures, 2008, 86(3/4/5): 473-482. |
| [19] |
Paul P S, Varadarajan A S, Vasanth X A, et al. Effect of magnetic field on damping ability of magnetorheological damper during hard turning[J]. Archives of Civil and Mechanical Engineering, 2014, 14(3): 433-443. DOI:10.1016/j.acme.2013.11.001 |
| [20] |
蔡永飞. 被动式电磁阻尼器对磁悬浮柔性转子振动控制的研究[D]. 南京: 南京航空航天大学, 2010. Cai Y F. Passive electromagnetic damper's effects on vibration control of flexible rotor-magnetic bearing system[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2010. (in Chinese) |








