2. 北京化工大学 智能过程系统工程教育部工程研究中心, 北京 100029
2. Engineering Research Center of Intelligent PSE, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
随着现代工业结构大型化、复杂化的发展趋势,工业系统运行过程中一处发生故障,潜在的连锁效应可能会导致巨大的经济损失[1],因此研究如何保证工业系统生产设备之间的安全、无故障运行显得尤为重要和迫切。工业系统的故障诊断主要集中于信号处理与诊断[2]、故障机理[3]、智能决策与诊断[4]等方面,并且都取得了显著的成果。但传统的基于分析模型[5-6]如状态估计、参数估计及基于经验知识[7-8]如专家系统、符号有向图等故障诊断的方法要求研究系统的机理过程和获取先验知识,而工业系统的不断复杂化使这个过程变得越来越困难。随着多学科交叉发展和网络技术的不断进步,基于网络的故障诊断方法如基于贝叶斯网络的故障诊断[9-10]、基于复杂网络的故障诊断[11]等成为新的研究热点。
现代化工过程中产生的数据代表着系统运行时的状态,基于数据驱动的故障诊断方法通过挖掘数据的潜在信息来发现系统的故障情况[12-13],而相似度度量是数据挖掘过程的重要问题,在众多相似度度量指标中,余弦相似度具有零不变性[14]、交叉性[15]等优点而被广泛研究与应用。因此,本文基于余弦相似度引入复杂网络理论,提出一种基于余弦相似度模型的化工过程异常检测方法,利用余弦相似度度量系统中各变量的相关性,以网络的形式呈现系统结构,并通过分析网络的复杂性指标与变量节点的属性变化实现Tennessee-Eastman(TE)过程故障检测,避免了经验知识获取的复杂以及经验知识不足而引起的偏差。最后通过实例与偏相关系数方法对比效果验证本文方法的有效性和准确性。
1 余弦相似度余弦相似度是一种计算相关性的方法,它是将个体的指标数据映射到向量空间,计算两个向量之间的夹角余弦值作为两个变量之间的相似性度量。夹角余弦值越大,表明两个向量之间的相似性越低;越小则相反。
两个向量m与n之间的余弦相似度计算公式为
| $ \cos \alpha = \frac{{\boldsymbol{mn}}}{{\left| \boldsymbol{m} \right|\;\left| \boldsymbol{n} \right|}} $ | (1) |
cosα为向量个体之间的相似度,取值范围为[-1,1]。个体变量x与y之间的相似度计算公式为
| $ \cos \left\langle {x, y} \right\rangle = \frac{{\sum\limits_{i = 1}^n {{x_i}{y_i}} }}{{\sqrt {\sum\limits_{i = 1}^n {x_i^2} } \sqrt {\sum\limits_{i = 1}^n {y_i^2} } }} $ | (2) |
其中,xi、yi分别表示变量x和y的第i个元素值。
2 基于余弦相似度的邻接矩阵构建对于TE过程数据,由于不同变量具有不同的单位和量级,为消除量纲影响, 对数据进行标准化,公式为
| $ x' = \frac{{x-\bar X}}{{{S_i}}} $ | (3) |
| $ \bar X = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} $ | (4) |
| $ {S_i} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i}-\bar X} \right)}^2}} } $ | (5) |
其中,
根据实际情况设定相似度阈值来确定变量之间的相似程度。针对本文提出的方法,阈值设定[16-17]如表 1所示。
| 下载CSV 表 1 余弦相似度对应变量相关性 Table 1 Cosine similarity corresponding to the variable correlations |
数据预处理后,由式(2) 计算各变量之间的余弦相似度值,再根据设定的阈值区间对应删除不相关的连接,构建邻接矩阵。由于余弦相似度值有正负之分,故定义在|cos 〈x, y〉|≥0.4时,若cos 〈x, y〉≥0,则邻接矩阵元素rxy=1,ryx=0;反之则邻接矩阵元素rxy=0,ryx=1。在|cos 〈x, y〉| < 0.4时,邻接矩阵元素rxy=0,ryx=0。在此基础上生成了邻接矩阵R如式(6)[16]
| $ \boldsymbol{R = }\left[{\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1n}}} \\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2n}}} \\ \vdots & \vdots &{}& \vdots \\ {{r_{n1}}}&{{r_{n2}}}& \cdots &{{r_{nn}}} \end{array}} \right] $ | (6) |
根据得到的邻接矩阵,确定对应变量之间的网络拓扑结构,再基于网络的研究形式对TE过程进行故障检测。
3 故障检测分析本文中主要是以网络形式呈现TE过程各变量之间的关系,故以复杂网络的拓扑性质度量指标作为故障检测分析的手段。
3.1 度量指标(1) 平均度
节点度指的是网络中和某节点相关联的边的条数,又称关联度,它是描述网络中节点属性的一个重要指标。特别地,对于有向图,节点的度为入度和出度总和,入度指进入该节点的边的条数,出度指从该节点出发的边的条数。网络节点平均度的计算公式为
| $ \bar K = \frac{1}{N}\sum\limits_{i = 1}^N {{k_i}} $ | (7) |
其中,N为网络中节点个数,ki为网络中节点的度。
(2) 集聚系数
图形理论中的集聚系数是指图中的点倾向于集聚在一起的程度。在实际网络中,集聚系数用来量化网络的集聚性,有向图中,ki个节点间可能存在的最大边数为ki(ki-1),故有向图中节点vi的集聚系数为
| $ C{l_i} = \frac{{{E_i}}}{{{k_i}\left( {{k_i}-1} \right)}} $ | (8) |
其中,Ei表示与节点vi连接的ki个节点之间实际存在边的数目,Cli越大说明节点vi局部集聚性越高。
整个网络的集聚系数为所有结点的局部集聚系数的均值,公式为
| $ \overline {Cl} = \frac{1}{N}\sum\limits_{i = 1}^N {C{l_i}} $ | (9) |
其中,N为网络中节点个数,
(3) 网络密度
网络密度指一个网络中各节点之间联络的紧密程度,是对图的完备性的一种测度,在一定程度上表征该网络中关系的数量与复杂程度。网络密度定义为
| $ d = \frac{{2m}}{{N\left( {N-1} \right)}} $ | (10) |
其中,N为网络中节点个数,m为网络中连边的总数。d的值介于0和1之间,当网络完全连通时,d=1;而实际网络的密度通常远小于1。
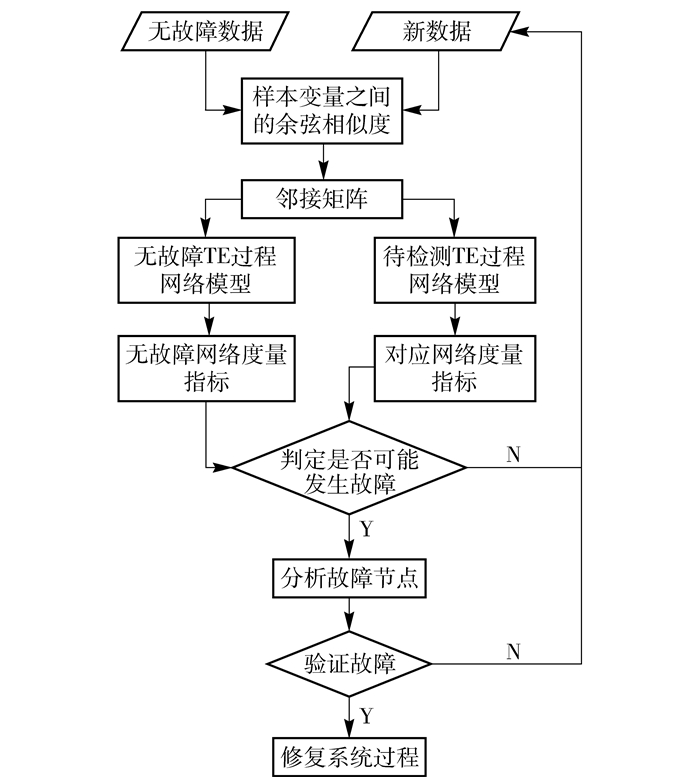
3.2 算法流程本文方法通过对比无故障数据与待检测数据对应的网络结构属性与指标的差异来进行故障检测。网络中单个节点属性的突变与度量指标的变化都表征了系统故障的发生,不同状态下的数据构建得到的网络拓扑结构是相异的。当系统发生故障时,某些变量的数据会发生明显的变化,并导致这些变量与其他变量之间的相关性发生较大变化;随之,整体得到的网络结构及对应网络度量指标也会产生变化,网络中相关性变化最明显的变量节点是最有可能的故障源。所提方法的流程如图 1所示,具体步骤如下。
|
图 1 算法流程图 Fig.1 Algorithm flowchart |
(1) 对无故障数据进行标准化预处理如式(3),通过余弦相似度(式(2))计算得到变量节点之间的相关性;根据表 1设置相关性阈值为0.4,得到系统无故障时对应的网络结构,计算网络中的度量指标。
(2) 选择系统运行时的数据进行标准化预处理;计算变量间的余弦相似度来度量变量节点间的相关性;构建对应的网络结构并计算相对应的网络指标。
(3) 对比步骤(1)、(2) 中的指标,判断系统是否发生了故障。若所有指标属于正常波动,则返回步骤(2),继续选取数据进一步验证;若有度量指标发生明显变化,则根据节点相关性变化来确定最有可能的故障源。
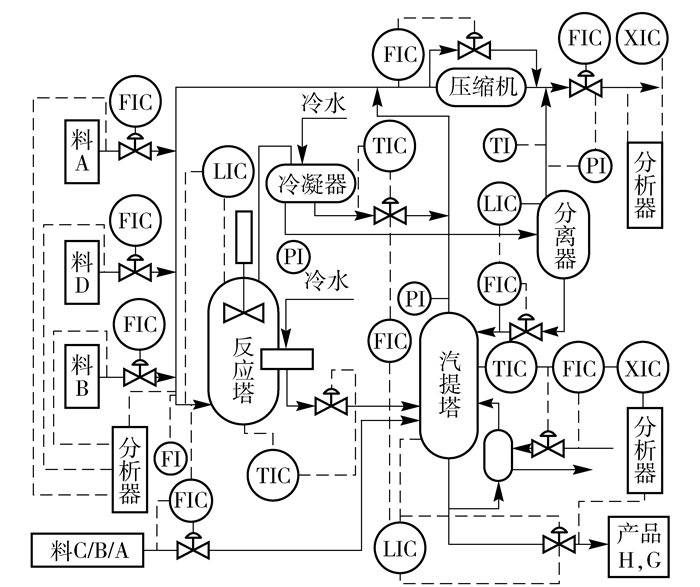
4 实验验证 4.1 实验设置采用TE数据集验证本文方法的有效性及其相对于偏相关系数方法的优越性。图 2所示是TE过程的工艺流程图,该过程共涉及41个测量变量和12个操作变量,而41个测量变量中有19个是组分变量。由于本文与偏相关系数方法进行比较,故保持数据变量一致(主要针对测量变量中的22个非组分变量)。表 2包含了对应的变量名称和编号。TE过程采用Matlab仿真模型[17],相关参数设置为:数据采样时长72 h,时间间隔0.01 h,故障时刻30 h。
|
图 2 TE过程的工艺流程图 Fig.2 TE process flow chart |
| 下载CSV 表 2 TE过程22个非组分变量名称及节点编号 Table 2 Variable name corresponding to node |
为了验证本文方法的效果,针对TE过程,通过实例对比本文方法与偏相关系数方法[18]分别在无故障与有故障时的网络结构与度量指标的相异性来分析故障检测效果。
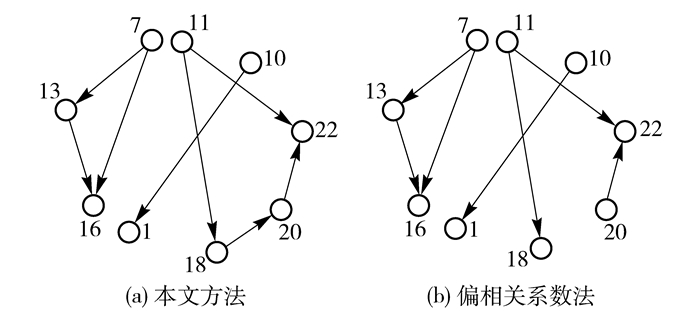
4.2.1 无故障TE过程在TE仿真模型中不设置任何故障,采集数据,运用本文方法与偏相关系数方法得到对应的网络结构(图 3),并分别计算网络度量指标。
|
图 3 无故障网络图 Fig.3 No fault network model |
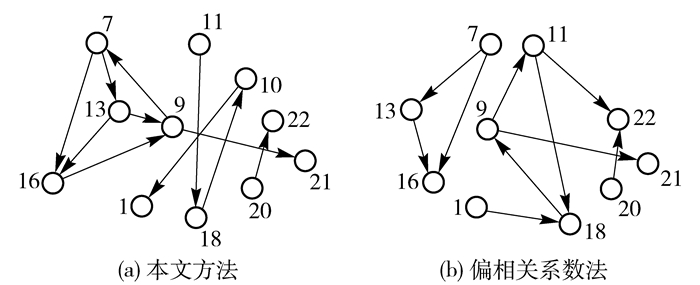
设置故障4(变化类型为阶跃),获取数据,运用本文方法和偏相关系数方法分别得到故障4时的网络图(图 4),分别对两种方法计算相关度量指标并与非故障情况对比,结果见表 3。
|
图 4 故障4时的网络图 Fig.4 Network model of fault 4 |
| 下载CSV 表 3 故障4与无故障时度量指标对比 Table 3 Network characteristic parameter comparison between fault 4 and no fault |
从图 3和图 4可看出,两种方法中节点9均从孤立节点变成了度值较大的节点,对比节点9在两种情况下与其他变量节点的相关性曲线(图 5)可看出,故障4下两种方法中节点9的相关性大小波动较明显;从表 3可看出,两种方法下,网络平均度和平均集聚系数都有明显增大,说明系统故障后,节点9出现的变化使得网络节点的集聚性变高且整个网络的紧密度增大。

|
图 5 故障4与无故障时节点9的相关性对比 Fig.5 Contrast of correlation about node 9 between fault 4 and no fault |
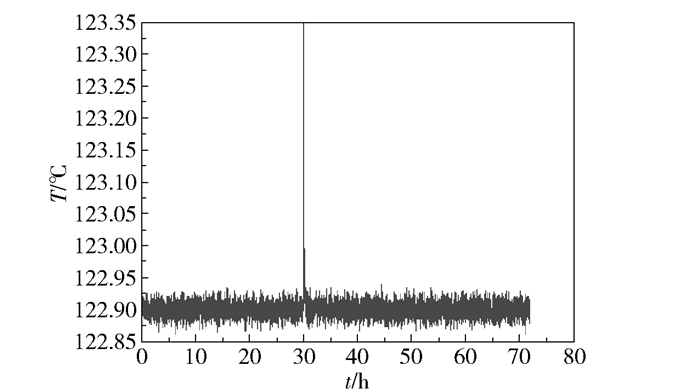
通过图 5可知,两种方法下,故障4时节点9在网络变化过程中相关性发生明显波动,而仿真模拟中故障4下节点9的运行数据(即反应器的温度T,余图同)发生了阶跃变化(图 6)。由此可见,本文方法与偏相关系数方法均有效地检测到了故障发生的节点9。
|
图 6 故障4时节点9的运行数据 Fig.6 Data curve of node 9 with fault 4 |
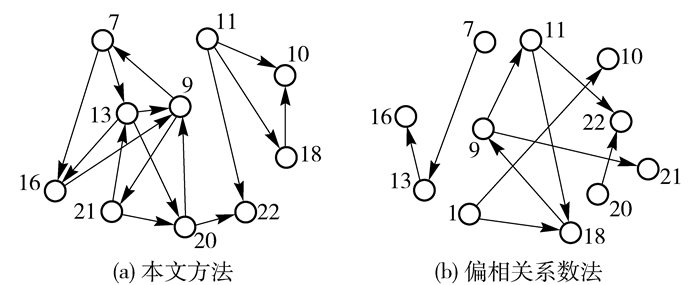
设置故障11(变化类型为随机),获取数据,运用本文方法和偏相关系数方法得到故障11时的网络图(图 7),分别对两种方法计算相关度量指标并与非故障数据对比,结果见表 4。
|
图 7 故障11时的网络图 Fig.7 Network model of fault 11 |
| 下载CSV 表 4 故障11与无故障时度量指标对比 Table 4 Network characteristic parameter comparison between fault 11 and no fault |
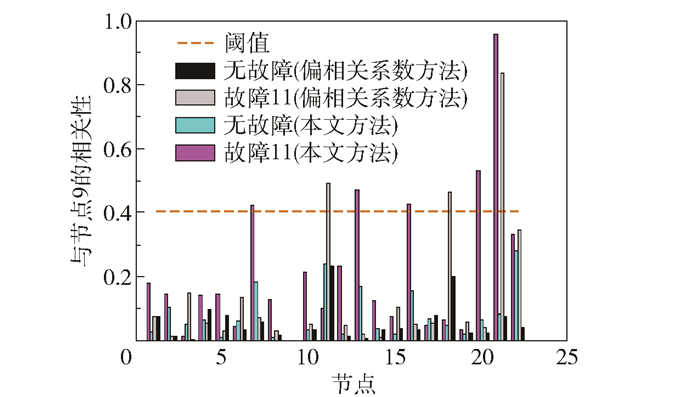
从图 3和图 7可看出,两种方法下,节点9在结构网络中从孤立节点变成了度值较大的节点,对比节点9在两种情况下与其他变量节点的相关性曲线(图 8),可看出故障11情况下,两种方法中节点9的相关性波动较明显。从表 4可看出,本文方法的网络平均度、平均集聚系数和网络密度都有明显增大,说明在节点9的变化下,网络中连接增多、节点的集聚性变高且整个网络的紧密度增大;偏相关系数方法的网络平均度和网络密度有一定幅度增加,但是平均集聚系数减小,说明网络中节点的平均集聚程度降低了。
|
图 8 故障11与无故障时节点9的相关性对比 Fig.8 Contrast of correlation about node 9 between fault 11 and no fault |
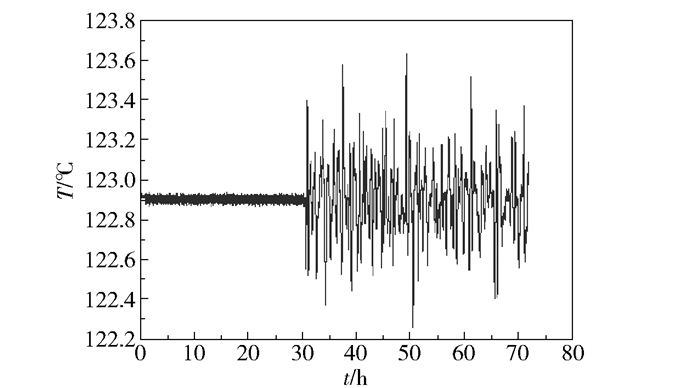
仿真模拟中,故障11时,节点9的运行数据在故障时刻之后发生了随机性变化,如图 9所示。由此可见,对于故障11,本文方法与偏相关系数方法均有效地检测到了故障发生的节点9。
|
图 9 故障11时节点9的运行数据 Fig.9 Data curve of node 9 with fault 11 |
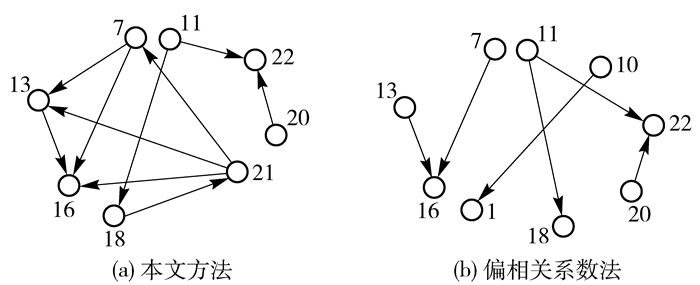
设置故障9(变化类型为随机),获取数据,运用本文方法和偏相关系数方法,分别得到故障9时的网络图(图 10)并计算对应网络的相关度量指标与非故障数据进行对比,结果见表 5。
|
图 10 故障9时的网络图 Fig.10 Network model of fault 9 |
| 下载CSV 表 5 故障9时与无故障时度量指标对比 Table 5 Network characteristic parameter comparison between fault 9 and no fault |
故障9及本文方法下,由图 3(a)和图 10(a)对比可看出,节点21从孤立节点变成度值较大的节点,由图 11看出其相关性发生了较大波动,由表 5看出故障9时节点21的变化使各度量指标均明显增大。而偏相关系数方法下,比较图 3(b)和图 10(b)可知,故障9时的网络图与无故障时没有明显变化,图 11表明节点21在网络变化过程中相关性没有太大波动,表 5中的度量指标也没有明显变化,其中集聚系数变为0是因为故障9时,网络中少了节点7和节点13的连边,导致使网络中唯一能体现节点集聚性的结构消失了。

|
图 11 故障9与无故障时节点21的相关性对比 Fig.11 Contrast of correlation about node 21 between fault 9 and no fault |
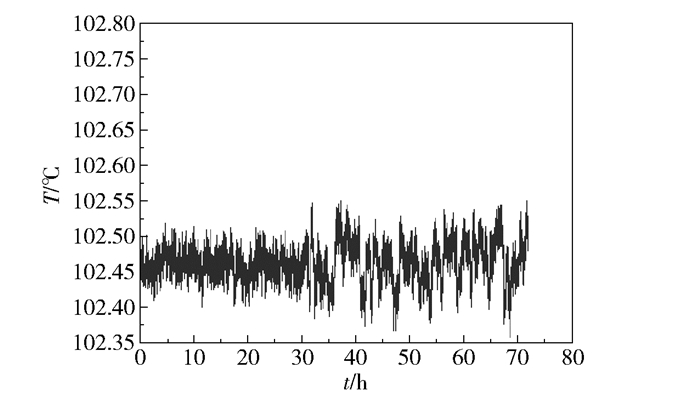
仿真模拟中故障9下,节点21的运行数据在故障之后发生了随机性变化,数据趋势没有故障之前那么紧密(图 12)。由此可见,对于故障9,本文方法有效地检测到了偏相关系数方法未检测到的故障节点21。
|
图 12 故障9时节点21的运行数据 Fig.12 Data curve of node 21 with fault 9 |
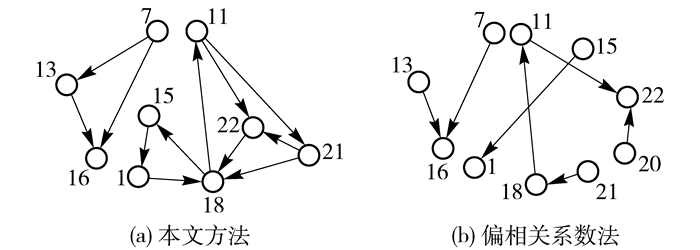
设置故障10(变化类型为随机),获取数据,运用本文方法和偏相关系数方法得到故障10时的网络图(图 13),并分别计算相关度量指标与非故障数据进行对比,见表 6。
|
图 13 故障10时的网络图 Fig.13 Network model of fault 10 |
| 下载CSV 表 6 故障10时与无故障时度量指标对比 Table 6 Network characteristic parameter comparison between fault 10 and no fault |
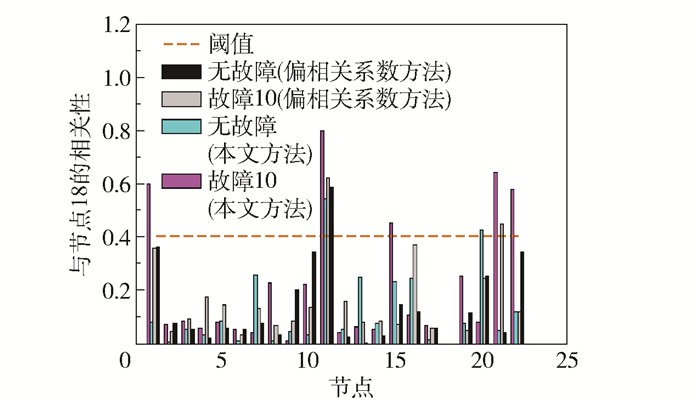
由图 3(a)和图 13(a)对比可看出,故障10下,本文方法中变量节点18的连接有较明显增加,其相关性发生了较大波动(图 14);且由表 6看出,节点18的变化使各度量指标都明显增大。而偏相关系数方法下,比较图 3(b)和图 13(b),故障10下的网络图与无故障时无明显变化,图 14表明变量节点18在网络变化过程中相关性也没有太大波动,表 6中度量指标也没有明显变化,其中集聚系数变为0是因为故障10时,网络中少了节点7和节点13的连边,导致网络中唯一的能体现节点集聚性的结构消失了。
|
图 14 故障10与无故障时节点18相关性对比 Fig.14 Contrast of correlation about node 18 between fault 10 and no fault |
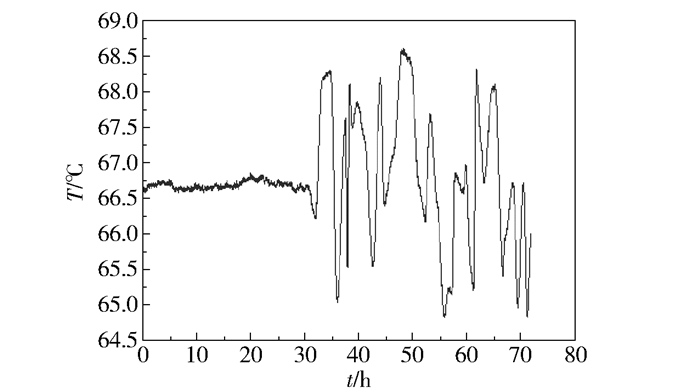
仿真模拟中,故障10下节点18的运行数据(即汽提塔温度T2)发生随机性变化如图 15所示。由此可见,对于故障10,本文方法有效地检测到偏相关系数方法未检测到的故障节点18。
|
图 15 故障10时节点18的运行数据 Fig.15 Data curve of node 18 with fault 10 |
本文针对TE过程系统提出了基于余弦相似度的复杂网络故障检测方法。根据余弦相似度,确定工业过程系统中变量之间的相关性,从而得到邻接矩阵构建网络结构,以直观形象的方式描述了工业系统设备变量之间的相互影响关系;通过TE过程故障分析实例及对比实验,检测到了偏相关系数方法检测不到的故障,验证了本文方法的有效性和准确性。本文方法不考虑工业系统运行的机理过程,直接从数据出发,从而避免了传统故障诊断方法需要大量经验知识的不足。后续研究中,将基于多源故障及如何实现自适应的故障诊断对本文方法进行进一步提升和完善。
| [1] |
钟群鹏, 张峥, 有移亮. 我国安全生产(含安全制造)的科学发展若干问题[J]. 机械工程学报, 2007, 43(1): 7-18. Zhong Q P, Zhang Z, You Y L. Several issues of scientific development of safety production (including safety manufacturing) in China[J]. Chinese Journal of Mechanical Engineering, 2007, 43(1): 7-18. (in Chinese) |
| [2] |
Gu F, Shao Y, Hu N, et al. Electrical motor current signal analysis using a modified bispectrum for fault diagnosis of downstream mechanical equipment[J]. Mechanical Systems and Signal Processing, 2011, 25(1): 360-372. DOI:10.1016/j.ymssp.2010.07.004 |
| [3] |
陈予恕. 机械故障诊断的非线性动力学原理[J]. 机械工程学报, 2007, 43(1): 25-34. Chen Y S. Nonlinear dynamical principle of mechanical fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2007, 43(1): 25-34. (in Chinese) |
| [4] |
Dou D Y, Zhou S S. Comparison of four direct classification methods for intelligent fault diagnosis of rotating machinery[J]. Applied Soft Computing, 2016, 46: 459-468. DOI:10.1016/j.asoc.2016.05.015 |
| [5] |
Cai J, Ferdowsi H, Sarangapani J. Model-based fault detection, estimation, and prediction for a class of linear distributed parameter systems[J]. Automatica, 2016, 66: 122-131. DOI:10.1016/j.automatica.2015.12.028 |
| [6] |
孙蓉, 刘胜, 张玉芳. 基于参数估计的一类非线性系统故障诊断算法[J]. 控制与决策, 2014, 29(3): 506-510. Sun R, Liu S, Zhang Y F. Fault diagnosis algorithm of a class of nonlinear system based on parameter estimation[J]. Control and Decision, 2014, 29(3): 506-510. (in Chinese) |
| [7] |
李楠楠, 郄志红, 古田均. 供水管网爆管故障诊断的PSO-SVM方法[J]. 系统工程理论与实践, 2012, 32(9): 2104-2110. Li N N, Qie Z H, Gu T J. PSO-SVM model for pipe bursting diagnosis of water supply network[J]. Systems Engineering-Theory & Practice, 2012, 32(9): 2104-2110. (in Chinese) DOI:10.12011/1000-6788(2012)9-2104 |
| [8] |
王雅琳, 何巍, 桂卫华, 等. 基于多块KPCA和SDG的故障诊断方法[J]. 控制与决策, 2013, 28(10): 1473-1484. Wang Y L, He W, Gui W H, et al. Fault diagnosis method based on MBKPCA and SDG[J]. Control and Decision, 2013, 28(10): 1473-1484. (in Chinese) |
| [9] |
Fernández-Cantí R M, Blesa J, Puig V. Set-membership identification and fault detection using a Bayesian framework[C]//2013 Conference on Control & Fault-tolerant Systems. Nice, France, 2013:572-577.
|
| [10] |
Cai B P, Liu H L, Xie M. A real-time fault diagnosis methodology of complex systems using object-oriented Bayesian networks[J]. Mechanical Systems and Signal Processing, 2016, 80: 31-34. DOI:10.1016/j.ymssp.2016.04.019 |
| [11] |
郑阳, 刘文颖, 温志伟, 等. 基于小世界网络的电网连锁故障实时搜索系统[J]. 电网技术, 2010, 34(7): 58-63. Zheng Y, Liu W Y, Wen Z W, et al. A real-time searching system for cascading failures of power grids based on small-world network[J]. Power System Technology, 2010, 34(7): 58-63. (in Chinese) |
| [12] |
耿志强, 姬威, 韩永明, 等. 基于维度最大熵数据流聚类的异常检测方法[J]. 控制与决策, 2016, 31(2): 343-348. Geng Z Q, Ji W, Han Y M, et al. Data stream clustering algorithm based on the maximum entropy of data dimension and its applications for anomaly detection[J]. Control and Decision, 2016, 31(2): 343-348. (in Chinese) |
| [13] |
Wang H, Chai T Y, Ding J L, et al. Data driven fault diagnosis and fault tolerant control:some advances and possible new directions[J]. Acta Automatica Sinica, 2009, 35(6): 739-747. |
| [14] |
Lee Y K, Kim W Y, Cai Y D, et al. CoMine:efficient mining of correlated patterns[C]//Proceedings of the Third IEEE International Conference on Data Mining. Piscataway, USA:IEEE, 2003:581-584.
|
| [15] |
Xiong H, Tan P N, Kumar V. Hyperclique pattern discovery[J]. Data Mining and Knowledge Discovery Journal, 2006, 13(2): 219-242. DOI:10.1007/s10618-006-0043-9 |
| [16] |
Han Y M, Geng Z Q, Gu X B, et al. Energy efficiency analysis based on DEA integrated ISM:a case study for Chinese ethylene industries[J]. Engineering Applications of Artificial Intelligence, 2015, 45: 80-89. DOI:10.1016/j.engappai.2015.06.008 |
| [17] |
Larsson T, Hestetun K, Hovland E, et al. Self-optimizing control of a large-scale plant:the Tennessee Eastman process[J]. Industrial & Engineering Chemistry Research, 2001, 40(22): 4889-4901. |
| [18] |
陈雨, 韩永明, 王尊, 等. 基于数据复杂网络理论的系统故障检测方法[J]. 化工学报, 2014, 65(11): 4503-4508. Chen Y, Han Y M, Wang Z, et al. System fault detection based on data-driven and complex networks theory[J]. CIESC Journal, 2014, 65(11): 4503-4508. (in Chinese) DOI:10.3969/j.issn.0438-1157.2014.11.041 |








