高精密光学元件研磨的加工形式有多种,其中游离磨料加工和固结磨料加工占主导地位[1-3]。与传统的游离磨料研磨加工相比,固结磨料研磨的磨粒固定在磨砂盘表面,研磨液是去离子水,通过磨盘的转动,对材料表面施加压力以实现去除功能[4]。固结磨料研磨速度快,提高了加工精度、加工质量和去除效率,并且具有较高的精度稳定性[5-6]。
对固结磨料研磨工具的材料去除特性已有大量研究。Fletcher等[7]使用金刚石固结磨料抛光盘打磨光学元件,结果表明此种打磨工具的材料去除率是散粒磨削加工去除率的3倍,并减少了30%的亚表面损伤。Tam等[8]研究了影响固着磨料研磨去除率和表面粗糙度的研磨参数如研磨相对速度、磨粒大小和研磨时间等。王毅等[9]提出了以趋近因子作为评价磨头参数优化的参量。Dong等[10-12]的研究表明采用有弹性的球表面研磨垫和不同打磨轨迹,可以有效减小光学元件的中频误差。Wang等[13-14]建立了固着磨料研磨的微观去除理论模型,比较了不同丸片规格的去除稳定性,并且建立了平转动单一丸片和多丸片的去除函数模型,但是未对常用的行星转动方式作出研究。
本文基于Preston方程,分析了行星转动加工方式的研磨过程中多丸片固结磨料在研磨接触区域的相对速度、接触时间和应力分布规律。建立多丸片固结磨料研磨的材料去除模型,通过分析趋近因子、去除函数归一化图形等参数,得到抛光盘的最优偏心比和速度比组合;分析了不同分布下抛光头的最大去除深度和去除量,为6种排布方式的固结磨料丸片在不同类型研磨中的使用提供理论依据。
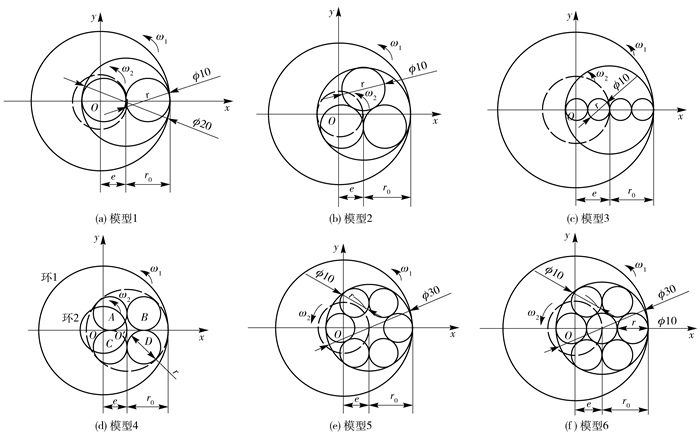
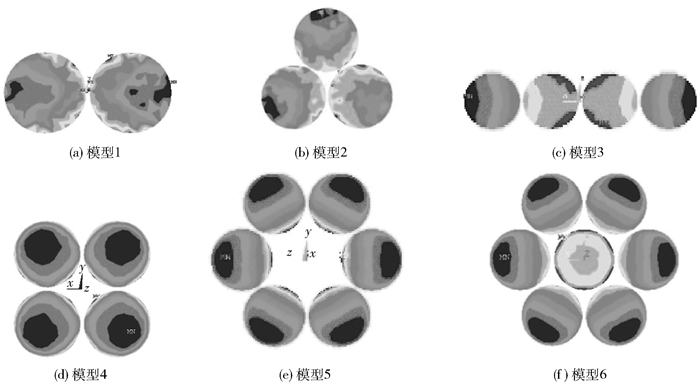
1 理论模型的建立 1.1 多丸片分布模型本文设计了6种多丸片固着磨料抛光盘,丸片数量从2个到7个,丸片排布呈直线排布、圆形排布、三角形排布和矩形排布多种情况,实际丸片排布模型如图 1所示,各模型抛光盘半径r0大小见表 1。
|
图 1 多丸片研磨头模型 Fig.1 Multidistribution pellet models of the grinding head |
| 下载CSV 表 1 多丸片排布研磨头各模型r0 Table 1 Multidistribution pellet models of the grinding head |
以图 1(d)中模型4为例,抛光盘行星转动,环1所包围的区域为打磨区域,环2为抛光盘中心的公转轨迹。在直角坐标系XOY中,O为公转圆的中心点,A、B、C和D分别为每个丸片的几何中心点,O’为抛光盘的几何中心点,同时也是抛光盘自转的中心点;抛光盘自转的角速度为ω1,行星运动公转角速度为ω2;每个丸片的半径为r;抛光盘的半径为r0,偏心距为e。
1.2 去除函数 1.2.1 模型构建Preston模型描述了光学加工中研磨效率和工艺参数间的关系,即在很大的数值范围内,研磨材料的去除量可以描述成一个线性方程:
| $ \Delta Z\left( {x, y} \right) = Kp\left( {x, y} \right)v\left( {x, y} \right) $ | (1) |
式中ΔZ(x, y)为研磨头与工件接触区域中任意点(x, y)单位时间内的材料去除量;K为Preston常数,通常与研磨工件材料、研磨液浓度、pH值相关;p(x, y)为(x, y)点的瞬时相对压强;v(x, y)表示(x, y)点的瞬时相对速度。结合式(1),则抛光盘的工作函数为
| $ Z\left( {x, y} \right) = \frac{1}{{T\left( {x, y} \right)}}Kp\left( {x, y} \right)\int_{T\left( {x, y} \right)} {v\left( {x, y} \right){\rm{d}}t} $ | (2) |
式中,T(x, y)表示点(x, y)在一个研磨周期中的研磨总时间。
1.2.2 接触时间模型4的行星运动的公转周期为T=2π/ω2,将周期T分成N份,每一份时间为Δt=T/N。在一个研磨周期内,抛光盘上各丸片中心A、B、C、D与抛光盘中心点O′的坐标可以表示为公式(3)。
| $ \left\{ {\begin{array}{*{20}{c}} {{x_A} = e{\rm{cos}}({\omega _2}t) + \sqrt 2 r{\rm{sin}}({\rm{\pi }}/4-{\omega _1}t)}\\ {{y_A} = e{\rm{sin}}({\omega _2}t) + \sqrt 2 r{\rm{sin}}({\rm{\pi }}/4-{\omega _1}t)}\\ {{x_B} = e{\rm{cos}}({\omega _2}t)-\sqrt 2 r{\rm{sin}}({\rm{\pi }}/4 - {\omega _1}t)}\\ {{y_B} = e{\rm{sin}}({\omega _2}t) - \sqrt 2 r{\rm{cos}}({\rm{\pi }}/4 - {\omega _1}t)}\\ {{y_C} = e{\rm{sin}}({\omega _2}t) - \sqrt 2 r{\rm{sin}}({\rm{\pi }}/4 - {\omega _1}t)}\\ {{y_D} = e{\rm{sin}}({\omega _2}t) + \sqrt 2 r{\rm{cos}}({\rm{\pi }}/4 - {\omega _1}t)}\\ {{x_C} = e{\rm{cos}}({\omega _2}t) + \sqrt 2 r{\rm{cos}}({\rm{\pi }}/4 - {\omega _1}t)}\\ {{x_{O'}} = e{\rm{cos}}({\omega _2}t)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ {{y_{O'}} = e{\rm{sin}}({\omega _2}t)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \end{array}} \right. $ | (3) |
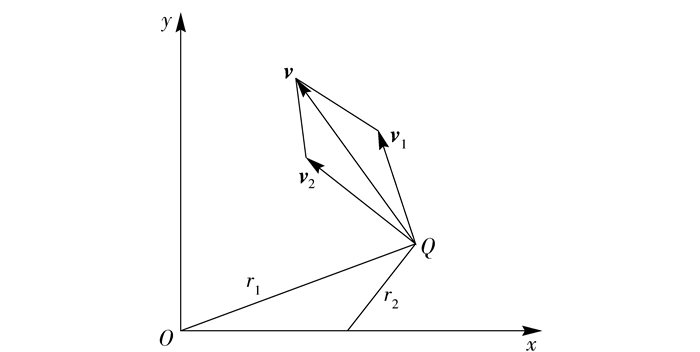
Q点是研磨区域内的任意一点,其坐标值为(x,y)。在一周期内Q点与抛光盘接触的总时间是tQ,初始位置时tQ=0。在任意时刻可以得到Q点到各丸片中心和抛光盘中心的距离
| $ {t_Q} = {t_Q} + \Delta t $ | (4) |
Q点与O′之间的距离为r1,与O之间的距离为r2,可以通过公式(5)、(6) 求得r1,r2:
| $ {r_1} = \sqrt {{{\left( {x-{x_{o'}}} \right)}^2} + {{\left( {y-{y_{o'}}} \right)}^2}} $ | (5) |
| $ {r_2} = \sqrt {{x^2} + {y^2}} $ | (6) |
则Q点的速度可以表示为:
| $ \begin{array}{l} \left| \boldsymbol{v} \right| = \left| {{\boldsymbol{v}_1} + {\boldsymbol{v}_2}} \right| = \sqrt {\left( {\boldsymbol{v}_1^2 + \boldsymbol{v}_2^2 + 2{\boldsymbol{v}_1}{\boldsymbol{v}_2}\cos \beta } \right)} = \\ \sqrt {{{\left( {{r_1}{\omega _1}} \right)}^2} + {{\left( {{r_2}{\omega _2}} \right)}^2} + 2{r_1}{\omega _1}{r_2}{\omega _2}\cos \beta } \end{array} $ | (7) |
式中v1、v2分别为Q点的自转速度和公转速度,v为合速度(图 2),β=arccos (r12+r22-e2)/(2r1r2)。
|
图 2 Q点速度分布 Fig.2 The velocity distribution at point Q |
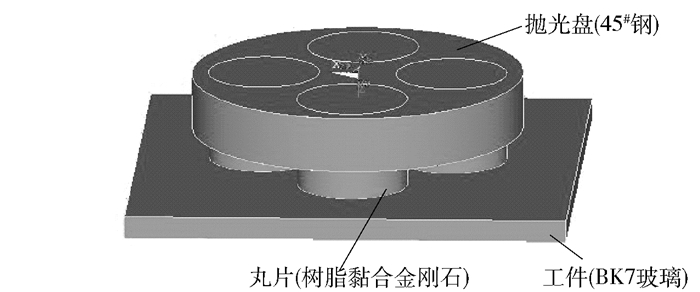
由于抛光盘结构的特殊性,研磨头与工件间接触力分布并不是均匀力,本文利用ANSYS分析抛光盘的压力分布,建立的仿真模型如图 3所示。模型由抛光盘(45#,Φ30 mm)、丸片(金刚石树脂Φ10 mm,厚度3 mm)和高精密光学元件(BK7玻璃,40 mm×40 mm×2 mm)3部分组成,各材料的力学参数见表 2。
|
图 3 ANSYS仿真几何模型 Fig.3 The FEA simulation 3D geometric model |
| 下载CSV 表 2 ANSYS模型中材料的力学参数 Table 2 The mechanical parameters of used materials in FEA model |
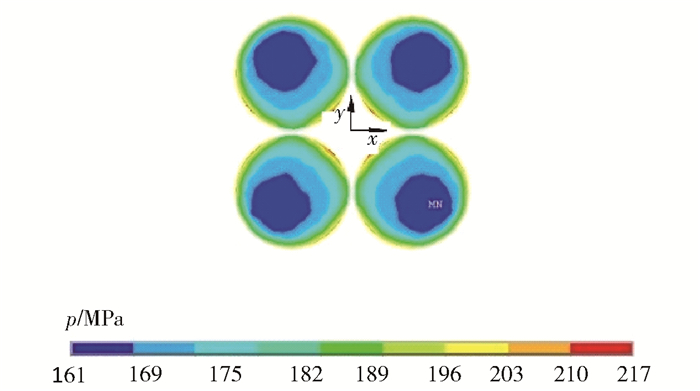
对以上ANSYS模型进行网格划分,定义丸片与光学元件为面面接触,工件的下表面固定0个自由度,并设置研磨头下压40 μm。图 4为仿真得到的丸片上的应力分布云图。可以看出,工件表面的压力并不是均匀分布的,越靠近抛光盘中心的压力越大,各丸片的边缘压力突变增大,最大压力为219.1 MPa,最小压力为162.0 MPa。丸片边缘范围内应力显著增大的现象主要是由应力集中引起的。
|
图 4 工件上的应力分布云图 Fig.4 The pressure distribution map of the workpiece |
提取沿直线y=x方向工件表面上500个点的应力值,拟合出y=-x轴上的应力曲线如图 5所示,其中压应力值沿y=x轴对称。为了方便计算,对该模型进行简化,用图 5中横坐标为x的所有点的压力值,表示工件表面上距离抛光盘中心为x的所有点的压力值,则可以得到工件表面压力拟合函数如公式(8) 所示:
| $ p\left( {x, y} \right) = p\left( {{r_1}} \right) $ | (8) |
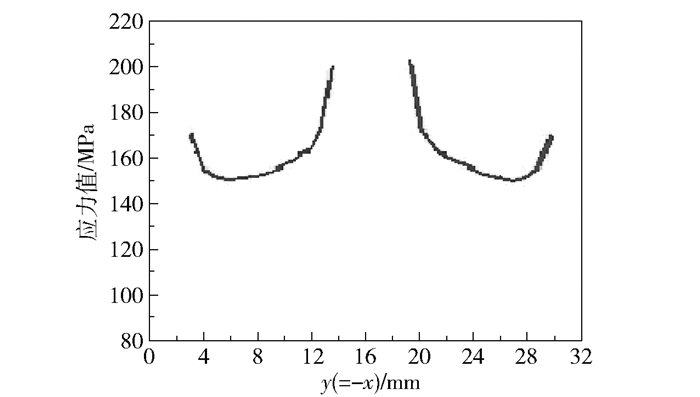
|
图 5 图 4中沿直线y=-x的丸片上各点应力曲线 Fig.5 The pressure values of workpiece on the -x-axis |
其中r1为函数自变量(即工件上点到抛光盘中心的距离)。
根据上述分析,结合公式(4)、(7)、(8) 及Preston方程,建立多丸片固结磨料抛光盘去除函数如下
| $ Z = \int_{{t_Q}} {Kp\left( {{r_1}} \right)\left( {{{\left( {{r_1}{\omega _1}} \right)}^2} + {{\left( {{{\left( {{r_2}{\omega _2}} \right)}^2}-2{r_1}{\omega _1}{r_2}{\omega _2}{\rm{cos}}\beta } \right)}^{\frac{1}{2}}}} \right){\rm{d}}t} $ |
已有文献表明[15],研磨工具去除函数的形状对于精密光学元件表面质量有很大的影响。去除函数中心去除量越大,面型误差越快收敛;当去除函数为δ函数时,则可以一次性收敛至目标值,但这在工程上是无法实现的。在实际中去除函数的形状越接近脉冲函数,其修正局部小残差的能力越强[15]。
为了获得更加接近脉冲函数的去除函数形状,需要对去除函数中多丸片分布的参数进行优化。根据去除函数模型,定义两个影响去除函数特性参数的变量:一个是速度比f,为抛光盘的自转速度与公转速度比,见公式(10);另一个是变量偏心比g,为抛光盘偏心距离与抛光盘半径之比,见公式(11)。则去除函数模型公式(9) 可以表示为式(12)。
| $ f = {\omega _1}/{\omega _2} $ | (10) |
| $ g = e/{r_0} $ | (11) |
| $ \begin{array}{*{20}{l}} {Z = \int_{{t_Q}} {Kp({r_1})({{({r_1}{\omega _2}f)}^2} + ({{({r_2}{\omega _2})}^2}}-2{r_1}{r_2}f\omega _2^2{\rm{cos}}\beta {)^{\frac{1}{2}}}){\rm{d}}t = }\\ {\int_{{t_Q}} {Kp({r_1})({{({r_1}{\omega _2}f)}^2} + {{(({x^2} + {y^2})\omega _2^2-2{r_1}{{({x^2} + {y^2})}^{\frac{1}{2}}}f\omega _2^2{\rm{cos}}\beta )}^{\frac{1}{2}}}){\rm{d}}t} } \end{array} $ | (12) |
式中r1=((x-gr0cos(ω2t))2+(y-gr0sin(ω2t))2)1/2
以模型4为例,根据已有文献[15]和正交实验结果,确定仿真各参数见表 3。利用MATLAB分别求得速度比范围(-5~5) 和偏心比范围(0.4~1.0) 的去除函数图像,得到去除函数图像的最高点为最大去除深度,并对去除函数进行积分,求得去除量。
| 下载CSV 表 3 MATLAB模拟去除函数参数 Table 3 The parameters of removal founction in MATLAB |
为了评价式(12) 去除函数与高斯脉冲函数的近似性,引进趋近因子概念[1]。趋近因子E定义为距离研磨区域中心点1/4范围内的研磨量Z1/4与去除量Z的比值,表达式为
| $ E = \frac{{{Z_{1/4}}}}{Z} $ | (13) |
E值越大,表示去除函数形状越接近脉冲函数,即去除函数的收敛效果越好。
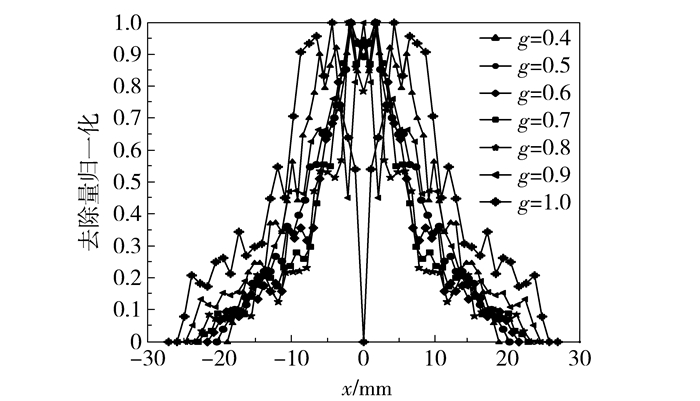
应用MATLAB计算1.3节中各去除函数曲线的趋近因子(表 4)。由表 4中数据可得,相同f下,当g=0.7时,去除函数趋近因子最大;当g=0.7、f =-1和-3时,趋近因子较大。g=0.7,f=-5、-3、-1、1、3、5时的去除函数曲线如图 6所示。可以看到当f=-1时,由于部分区域合速度为零,去除函数的去除半径变小,去除函数形状并不理想。通过上述趋近因子的比较,可得到模型4在所计算范围内的最优机构参数为g=0.7,f=-3。f=-3,g=0.4、0.5、0.6、0.7、0.8、0.9和1.0时的去除函数曲线如图 7所示。由图 6可知,转速比f主要影响去除去量,当f=1和-1时由于合速度大小为0,部分研磨区域没有材料去除。由图 7可知,偏心比g主要影响去除区域的半径及去除函数曲线的峰值,当g=1时曲线有两个相等的峰值,抛光中心的去除量为0,误差收敛速度慢,会增加光学元件的高频误差;当g=0.6和0.7时曲线有一个峰值且较大,分别为1.85×10-3 mm3、1.87×10-3 mm3,去除效果较好。
| 下载CSV 表 4 模型4在不同偏心比和不同速度比下去除函数的趋近因子 Table 4 The removel founctions tending genes of model 4 with different speed ratio and eccentricity |
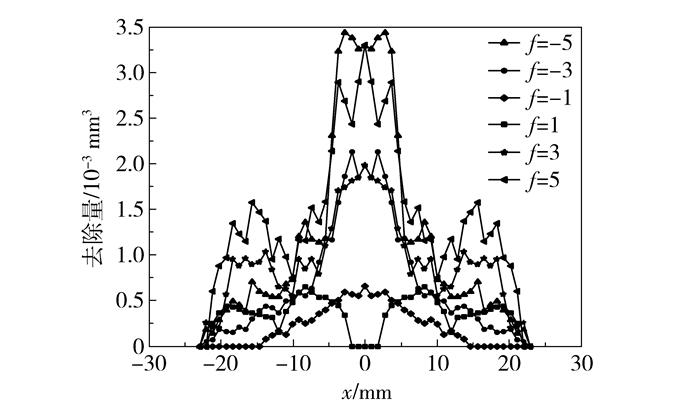
|
图 6 g=0.7时不同转速比下去除函数 Fig.6 The removal functions of model 4 under the condition g=0.7 with different speed ratios |
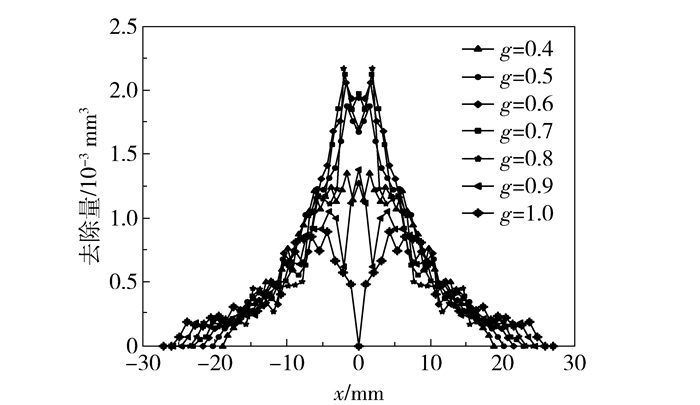
|
图 7 f=-3时不同偏心比下去除函数 Fig.7 The removal functions of model 4 under the condition f=-3 with different eccentricity values |
为了进一步确定去除函数的近高斯性,将图 6、7中的函数曲线归一化处理后如图 8、9所示。由图中可以得到,g=0.7、f=-3时,去除函数曲线更加接近高斯脉冲曲线;f=-3,g=0.6、0.7时,去除函数曲线更加接近高斯脉冲曲线,计算结果与趋近因子类似,从而验证了趋近因子的计算结果。
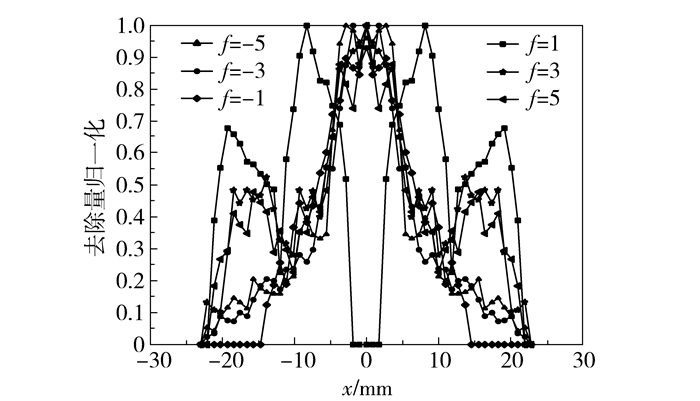
|
图 8 g=0.7时不同转速比下归一化去除函数 Fig.8 The normalized removal functions of model 4 under the condition g=0.7 with different speed ratios |
|
图 9 f=3时不同偏心比下归一化去除函数 Fig.9 The normalized removal functions of model 4 under the condition f=3 with different eccentricity values |
应用2.2~2.3节的方法,求得多丸片排布6种模型的压力分布云图如图 10所示,压力曲线如图 11所示,并计算出速度分布,求得各模型的去除函数。通过比较趋近因子和归一化曲线,确定各模型研磨时的最优f、g值,并计算出在最优参数下各模型的最大去除深度和去除量,计算结果见表 5。
|
图 10 6个模型应力分布云图 Fig.10 Pressure distribution maps for the six models |

|
图 11 6个模型应力分布曲线 Fig.11 Pressure value for the six models |
| 下载CSV 表 5 多丸片分布模型最优参数和去除量 Table 5 Models of the multi-distribution fixed abrasive pellets |
6个模型在最优化参数下的去除函数曲线及归一化曲线如图 12所示。图 12显示,模型3中由于4个丸片直线排布,去除函数近高斯性较弱,其余模型的去除函数曲线都有较好的近高斯性,适用于研磨加工。其中模型1和模型2的最大去除深度为1.2 mm、1.7 mm,去除量为15.3×10-3 mm3、23.7×10-3 mm3;模型5和模型6由较多丸片构成,最大去除深度为2.4 mm、2.3 mm,去除量为40.5×10-3 mm3、42.5×10-3 mm3。对比6种模型的归一化去除曲线及表 6中6种模型的趋近因子可知,模型4与模型5的曲线平滑,最大趋近因子分别为0.5971和0.6182。
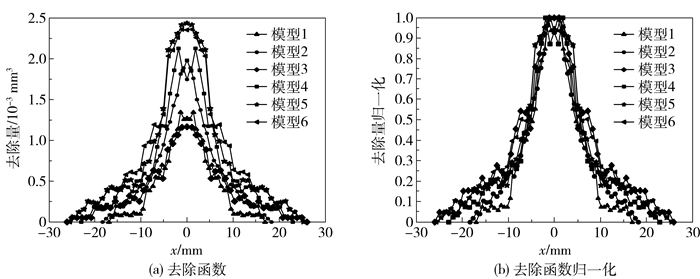
|
图 12 6种丸片排布最优去除函数曲线 Fig.12 The removal functions of different 6 models |
| 下载CSV 表 6 6种丸片排布的趋近因子 Table 6 The tending genes of 6 different distribution models |
(1) 对比在不同偏心比和不同转速比下函数曲线的趋近因子和归一化形状,得到了各模型研磨加工的最优参数:模型1和模型2的最大去除深度分别为1.2 mm、1.7 mm,去除量分别为15.3×10-3 mm3、23.7×10-3 mm3,适用于小去除量精密光学元件研磨加工;模型5和模型6的最大去除深度为2.4 mm、2.3 mm,去除量为40.5×10-3 mm3、42.5×10-3 mm3,适用于较大去除量精密元件研磨加工。
(2) 模型4与模型5的曲线趋近因子较大,曲线平滑且有更好的近高斯性,适用于减少光学元件表面局部误差的加工。
| [1] |
唐晓骁. 固结磨料研磨抛光垫基体的砂浆磨损特性研究[D]. 南京: 南京航空航天大学, 2013: 3-7. Tang X Y. Slurry abrasion characteristic of fixed abrasive pad[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2013:3-7. (in Chinese) |
| [2] |
王旭, 张峰, 张学军. 固着磨料抛光碳化硅反射镜的去除函数[J]. 光学精密工程, 2009, 17(5): 951-957. Wang X, Zhang F, Zhang X J. Removal function of computer controlled polishing SiC mirror with fixed abrasive[J]. Optics and Precision Engineering, 2009, 17(5): 951-957. (in Chinese) |
| [3] |
王旭. 固着磨料数控加工碳化硅反射镜工艺研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2010: 7-12. Wang X. Experimental study on computer controlled grinding and polishing SiC mirror with fixed abrasive[D]. Changchun:Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2010:7-12. (in Chinese) |
| [4] |
墨洪磊, 朱永伟, 唐晓潇, 等. 固结磨料研磨K9玻璃的工艺优化[J]. 金刚石与磨料磨具工程, 2012, 32(3): 7-11. Mo H L, Zhu Y W, Tang X X, et al. Parameter optimization when lapping K9 glass with fixed abrasive pad[J]. Diamond & Abrasives Engineering, 2012, 32(3): 7-11. (in Chinese) |
| [5] |
王黎明, 田春林, 周化文. 平面光电器件的纳米级高速研磨[J]. 长春理工大学学报, 2004, 27(3): 18-19. Wang L M, Tian C L, Zhou H W. High speed nanometer lapping photoelectric elements[J]. Journal of Changchun University of Science and Technology, 2004, 27(3): 18-19. (in Chinese) |
| [6] |
李立明, 李茂, 朱永伟. 固结磨料研磨与抛光的研究现状与展望[J]. 金刚石与磨料磨具工程, 2009(5): 17-22. Li L M, Li M, Zhu Y W. Fixed abrasive lapping and polishing:present situation and prospect[J]. Diamond & Abrasives Engineering, 2009(5): 17-22. (in Chinese) |
| [7] |
Fletcher T D, Gobena F T, Romero V D. Diamond fixed abrasive lapping of brittle substrates[C]//OSA Optical Fabrication & Testing Topical Meeting. Rochester, USA, 2004.
|
| [8] |
Tam H Y, Cheng H B, Wang Y W. Removal rate and surface roughness in the lapping and polishing of RB-SiC optical components[J]. Journal of Materials Processing Technology, 2007, 192/193: 276-280. DOI:10.1016/j.jmatprotec.2007.04.091 |
| [9] |
王毅, 余景池. 计算机控制光学表面抛光的磨头运动方式和参数的优化研究[J]. 光学技术, 2003, 29(3): 258-260. Wang Y, Yu J C. Studying and optimizing running mode and parameter of polishing tool used in computer controlled polishing of optical surface[J]. Optical Technique, 2003, 29(3): 258-260. (in Chinese) |
| [10] |
Dong Z C, Cheng H B. Study on removal mechanism and removal characters for SiC and fused silica by fixed abrasive diamond pellets[J]. International Journal of Machine Tools and Manufacture, 2014, 85(5): 1-13. |
| [11] |
Dong Z C, Cheng H B, Tam H Y. Investigation on removal features of multi distribution fixed abrasive diamond pellets used in the polishing of SiC mirrors[J]. Applied Optics, 2012, 51(35): 8373-8382. DOI:10.1364/AO.51.008373 |
| [12] |
Dong Z C, Cheng H B, Tam H Y. Further investigations on fixed abrasive diamond pellets used for diminishing mid-spatial frequency errors of optical mirrors[J]. Applied Optics, 2014, 53(3): 327-334. DOI:10.1364/AO.53.000327 |
| [13] |
Wang X, Zheng L G. Theoretical study on removal rate and surface roughness in grinding a RB-SiC mirror with a fixed abrasive[J]. Chinese Optics Letters, 2012, 10(Suppl): S12201. |
| [14] |
Wang X, Zhang X. Study on experiment of grinding SiC mirror with fixed abrasive[C]//Proceedings of SPIE. Chengdu, 2009, 7282:72820K.
|
| [15] |
李全胜. 计算机控制光学表面成形驻留时间算法研究[J]. 光学技术, 1999(3): 56-59. Li Q S. Dwell time algorithm in computer controlled optical surfacing[J]. Optical Technique, 1999(3): 56-59. (in Chinese) |








