2. 中石油西气东输管道公司 厦门分公司, 福建 厦门 361000
2. Petrochina West-East Gas Pipeline Company, Xiamen Operation Department, Xiamen, Fujian 361000, China
上世纪五十年代初,卧式螺旋卸料沉降离心机开始应用于石油钻井行业中。被用作泥浆处理的钻井液离心机,由于具有工作连续、维修方便、对物料适应性强、可分离固相颗粒粒径范围广等优点,逐渐成为固控系统中一个必不可少的装置[1-2]。然而一直以来离心机的发展都是理论研究远落后于实践[3],时至今日,针对钻井液离心机工艺理论计算方面的研究依然薄弱,已有的理论计算公式无法有效、准确地预测机器性能和指导设计[4]。
钻井液离心机作为最后一级固控设备,其泥浆处理效果直接影响着钻井的效率和安全[5],因此对离心机的分离效果进行预测具有重要意义[6]。而要探讨离心机的分离效率,就必须先了解固相颗粒在离心机中的沉降规律。目前常用的离心机沉降模型, 如传统离心机沉降模型等大都建立在“∑理论”之上,主要的离心机内流场相关理论如离心机生产能力的计算、临界分离粒径的计算等,都以“∑理论”作为基础[7-9]。
本文在前人研究的基础上充分考虑钻井液离心机的结构特点和工作原理,提出钻井液离心机沉降模型,旨在更加准确地描述固相颗粒在钻井液中的沉降规律,并以此为基础推导了钻井液离心机捕集效率的计算公式,建立了钻井液离心机捕集效率、结构参数、操作参数和钻井液参数之间的关系表达式。
1 离心机捕集效率计算方法目前两种主要的离心机捕集效率计算方法均以传统离心机沉降模型为基础,基于实现固液分离的基本条件:颗粒在到达溢流口位置之前就已经沉降到转鼓壁面[7]。
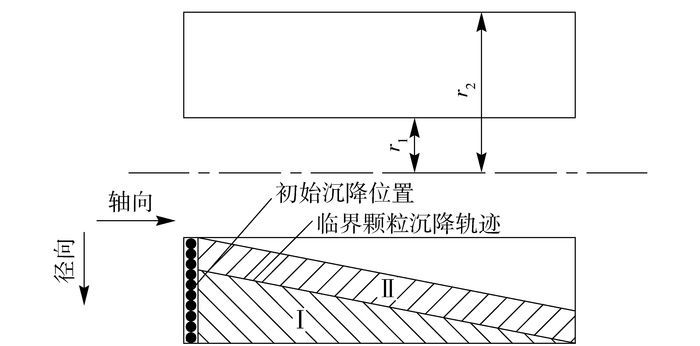
第一种方法如图 1所示,临界颗粒沉降轨迹将沉降区分为沉降完成区Ⅰ和沉降不可完成区Ⅱ,并利用位于Ⅰ区和Ⅱ区固相颗粒的数量关系得到颗粒捕集效率计算公式为[7]
|
图 1 传统离心机沉降模型 Fig.1 The classic sedimentation model |
| $P = \frac{{r_2^2}}{{r_2^2 - r_1^2}}\left[ {1 - {\rm{exp}}\;\left( {\frac{{ - 2{u_{\rm{t}}}{V_{\rm{c}}}{\omega ^2}}}{{Qg}}} \right)} \right]\lambda $ | (1) |
其中λ=60%,为效率因子。
该模型在建立过程中假设悬浮液均匀分布[7],但是由于颗粒沉降作用,使沉降池中悬浮液密度分布不均匀,而在钻井液离心机中钻井液由螺旋推料器的内筒经布料口进入转鼓,该布料口开口方向垂直于径向,不会出现传统离心机沉降模型中在沉降开始时颗粒沿径向均布的情况。这将导致过高估算能够完成分离的悬浮液体积,从而引起计算结果偏大,因此将该沉降模型应用于钻井液离心机分离效率的计算上会引起较大的偏差。
另一种离心机捕集效率的计算方法则是建立在固相颗粒粒径和临界颗粒粒径的相对大小关系的基础上。首先通过常用沉降模型计算出离心机能分离的临界颗粒粒径,然后利用公式(2) 计算出该粒径颗粒的捕集效率[8]
| $P = \frac{{r_2^2}}{{r_2^2 - r_1^2}}\left[ {1 - {\rm{exp}}\;\left( {\frac{{2d_x^2}}{{d_{\rm{c}}^2}}{\rm{ln}}\frac{{{r_1}}}{{{r_2}}}} \right)} \right]$ | (2) |
该理论利用固相颗粒粒径和沉降时间之间的关系,建立了离心机捕集效率计算式。不过该理论假设所有颗粒从同一个位置点开始进行沉降运动,但在实际情况中,固相颗粒经布料口进入转鼓后,是从沉降池自由液面上一定范围内开始进行沉降的,由于忽略了颗粒初始沉降位置对颗粒捕集效率的影响,从而存在较大的计算误差。因此,建立充分考虑初始沉降位置对离心机分离效果影响的离心机沉降模型,是提高捕集效率理论计算精度的重要研究方向。
2 钻井液离心机沉降模型 2.1 假设为了方便进行理论研究并降低计算难度,对钻井液离心机的沉降过程做如下假设:
(1) 所有颗粒在初始沉降位置均匀分布;
(2) 固相颗粒与液相在轴向运动过程中无相对滑移。
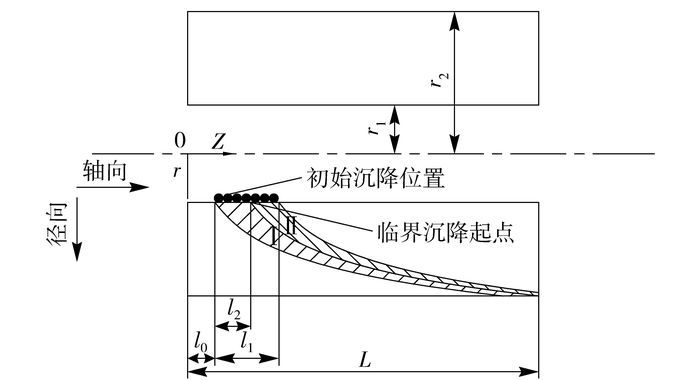
2.2 模型概述图 2是钻井液离心机沉降池的横截面图,它展示了钻井液离心机沉降模型的基本原理:在沉降开始时固相颗粒在自由液面上均匀分布,而分布区域的长度由布料口的形式和大小决定。该沉降模型采用笛卡尔坐标系,Z轴沿转鼓轴向,r轴则沿径向。
|
图 2 钻井液离心机沉降模型 Fig.2 Sedimentation model of a drilling fluid centrifuge |
捕集效率的定义是:在某一操作参数组合条件下,离心机对某种材料中某一粒径的固相颗粒的分离情况[9]。在图 2中,如果所有某粒径颗粒沉降到转鼓壁所需时间均小于颗粒停留在沉降池中的时间,则该粒径颗粒的捕集效率为100%;如果该粒径颗粒中只有部分颗粒达到上述条件,则称该粒径颗粒被部分捕集。已知固相颗粒的运动轨迹取决于颗粒速度,而在层流条件下,颗粒速度的位置变量只有颗粒所处位置的半径r,所以在确定的操作参数和钻井液参数下,某粒径固相颗粒的沉降轨迹形状是唯一的[7],只是由于不同的沉降起点导致颗粒停留在转鼓里的时间不同,从而影响捕集效率。因此对离心机捕集效率的研究可以转化为对固相颗粒沉降轨迹以及捕集效率和沉降起点关系的研究。本文定义初始沉降位置为颗粒沉降开始时在沉降池自由液面上所占据的一定平面空间,在离心机轴向截面上表现为沿轴向的一条线段(图 2中黑色圆形颗粒所在位置),大小为布料口宽度;临界颗粒沉降轨迹为某粒径颗粒的沉降终点位于溢流口的那条轨迹;临界沉降起点则是指临界颗粒沉降轨迹的起点。在所有位于初始沉降位置的颗粒中临界沉降起点与底流端之间的颗粒(图 2中区域Ⅰ的颗粒)能够在随液相运动到溢流口之前完成沉降,从而被捕集;而另外一部分颗粒(图 2中区域Ⅱ的颗粒)无法被捕集。因此某一粒径颗粒的捕集效率等于初始沉降位置中临界沉降起点靠近底流端方向的颗粒与初始沉降位置中全部颗粒数量的比值(图 2中位于区域Ⅰ的颗粒与全部颗粒数量的比值)。
2.3 固相颗粒运动时间进入转鼓后颗粒的运动由两个方向的运动合成,一个是沿径向的沉降运动,另一个是随液体沿轴向的迁移运动。由于在模型建立阶段假设固相颗粒与液相在轴向运动中无相对滑移,所以将固相颗粒的轴向运动问题转化为离心机内液相的轴向运动问题。
关于离心机转鼓内液相的流动问题前人已经进行了大量的研究,本文在对各种理论进行研究之后选择最符合钻井液离心机内流场流动特性的理论—液体沿螺旋流道流动模型。该模型在传统的层流理论用连续性方程和纳维-斯托克斯方程求解速度的基础上增加了流体沿螺旋流道流动的运动条件方程,从而得出流体的轴向运动速度[10]
| $\frac{{{\rm{d}}Z}}{{{\rm{d}}t}} = {u_z} = \frac{{Q({r_2} - r)}}{{{\rm{\pi }}{{({r_2} - {r_1})}^2}r}}$ | (3) |
其中r是流体所处位置半径。
根据斯托克斯定理[9],固相颗粒在离心力场中的自由沉降速度可以表示为
| ${u_{\rm{t}}} = \frac{{d_x^2}}{{18\mu }}({\rho _{\rm{s}}} - {\rho _{\rm{l}}})r{\omega ^2}$ | (4) |
由于离心机分离的悬浮液固相体积分数往往大于0.5%,这种情况下固相颗粒之间的机械碰撞不能忽略,固相颗粒在离心力场中发生干涉沉降[11-12]。目前常用的方法是对自由沉降中的斯托克斯定理引入修正系数[13]。本文假设沉降运动处于层流区,空隙函数采用Richardson -Zaki方程
| ${u_r} = {u_{\rm{t}}}{\varepsilon ^2}f\left( \varepsilon \right)$ | (5) |
其中,ε为悬浮液中液相体积分数,f(ε)=ε2.65为空隙函数Richardson-Zaki方程[13]。
得到固相颗粒的干涉沉降速度
| $\frac{{{\rm{d}}r}}{{{\rm{d}}t}} = {u_r} = \frac{{d_x^2}}{{18\mu }}({\rho _{\rm{s}}} - {\rho _{\rm{l}}})r{\omega ^2}{\varepsilon ^{4.65}}$ | (6) |
由2.2节的分析可知,某粒径颗粒的临界沉降起点决定了其捕集效率的大小,不同的沉降起点导致颗粒的轴向位移不同,从而影响了轴向运动所需时间。悬浮液由布料口进入沉降池,固相颗粒在自由液面上的一定范围内随机分布,因此可以假设颗粒在初始沉降位置均匀分布。2.2节中提到,某一粒径颗粒的捕集效率等于初始沉降位置中临界沉降起点靠近底流端方向的颗粒与初始沉降位置中全部颗粒数量的比值,因此捕集效率的数学定义可以由数量比转化为初始沉降位置中临界沉降起点靠近底流端方向的面积与初始沉降位置所占面积的比值。又由于离心机转鼓是一个轴对称图形,所以捕集效率转化为初始沉降位置中临界沉降起点靠近底流端方向的长度与初始沉降位置长度的比值(图 2中l2和l1的比值),如方程(7) 所示
| $P = \frac{{{l_2}}}{{{l_1}}}$ | (7) |
由图 2可以看出,颗粒的最大轴向位移为
| ${S_{\rm{Z}}} = L - {l_0} - P{l_{\rm{1}}}$ | (8) |
其中,L为离心机柱段长度,l0为底流端初始沉降位置端点与柱段起点之间的距离, l1为初始沉降位置的长度,等于布料口宽度,P为离心机固相捕集效率。
如图 2所示,建立笛卡尔坐标系,坐标原点为柱段起点在轴线上的投影。固相颗粒沉降轨迹可以表示为[14]
| $\frac{{{\rm{d}}r}}{{{u_r}}} = \frac{{{\rm{d}}Z}}{{{u_z}}}$ | (9) |
将方程(3)、(6) 带入方程(9),整理后得
| $\frac{{18\mu Q({r_2} - r)}}{{{\rm{\pi }}d_x^2({\rho _{\rm{s}}} - {\rho _{\rm{l}}}){\omega ^2}{\varepsilon ^{4.65}}{{({r_2} - {r_1})}^2}{r^2}}}{\rm{d}}r = {\rm{d}}Z$ | (10) |
颗粒在离心力场中被捕集的临界条件为:颗粒在转鼓中的停留时间等于颗粒沉降到转鼓壁的时间,即颗粒的沉降终点恰好位于溢流口。因此临界沉降轨迹的边界条件为
| $\begin{array}{*{20}{l}} {{Z_{(r = {r_1})}} = {l_0} + {l_2} = {l_0} + P{l_1}}\\ {{Z_{(r = {r_2})}} = L} \end{array}$ |
在边界条件下求解方程(10) 可得钻井液离心机捕集效率,为
| $P = \frac{{L - {l_0} - \frac{{18\mu Q}}{{{\rm{\pi }}d_x^2({\rho _{\rm{s}}} - {\rho _{\rm{l}}}){\omega ^2}{\varepsilon ^{4.65}}{{({r_2} - {r_1})}^2}}}\left( {\frac{{{r_2}}}{{{r_1}}} - 1 - {\rm{ln}}\frac{{{r_2}}}{{{r_1}}}} \right)}}{{{l_1}}}$ | (11) |
方程(11) 描述了钻井液离心机捕集效率的计算方法,但是由于两方面的原因使方程用于实际工程计算还需要进行修正:第一,理论模型没有考虑湍流和涡流的影响,对颗粒碰撞和能量损耗的考虑也不够全面;第二,在理论研究中假设所有完成沉降的颗粒都能够被捕集,但是在实际情况下,沉降颗粒在卸料过程中依然存在一定的损耗。因此引入效率因子λ,λ=60%,该因子由Rushton等[7]提出。
方程(11) 描述了钻井液离心机捕集效率与离心机操作参数、结构参数以及钻井液参数之间的关系,这有利于定量地研究各参数对离心机分离效果的影响,从而能够针对不同钻井液选出最合适的离心机和最优操作参数组合。
2.5 适用性分析方程(11) 的建立基于临界颗粒沉降轨迹和临界沉降起点与捕集效率的关系,因此该方程只适用于具有临界颗粒沉降轨迹的颗粒。事实上不是所有粒径的颗粒都具有临界颗粒沉降轨迹,该轨迹与材料的性质和离心机的各项参数有关。为了方便进行方程(11) 的适用性探讨,定义参数la为在给定参数条件下某粒径颗粒沉降到转鼓壁时轴向需要移动的距离,如式(12) 所示
| ${l_{\rm{a}}} = L - {l_0} - \frac{{18\mu Q}}{{{\rm{\pi }}d_x^2({\rho _{\rm{s}}} - {\rho _{\rm{l}}}){\omega ^2}{\varepsilon ^{4.65}}{{({r_2} - {r_1})}^2}}}\left( {\frac{{{r_2}}}{{{r_1}}} - 1 - {\rm{ln}}\frac{{{r_2}}}{{{r_1}}}} \right)$ | (12) |
如图 2所示,颗粒拥有临界颗粒沉降轨迹的条件为la∈[L-l0-l1, L-l0],所以方程(11) 的使用条件为la∈[L-l0-l1, L-l0]。经研究发现,当la<L-l0-l1时,该粒径的所有颗粒均能在随液相排出离心机之前完成沉降,因此P=1;当la>L-l0时,该条件下任何位置的颗粒均不能完成沉降,因此P=0。所以钻井液离心机捕集效率可以写为
| $P = \left\{ {\begin{array}{*{20}{l}} 0&{{l_{\rm{a}}} > L - {l_0}}\\ {\frac{{L - {l_0} - \frac{{18\mu Q}}{{\pi d_x^2({\rho _{\rm{s}}} - {\rho _{\rm{l}}}){\omega ^2}{\varepsilon ^{4.65}}{{({r_2} - {r_1})}^2}}}\left( {\frac{{{r_2}}}{{{r_1}}} - 1 - {\rm{ln}}\frac{{{r_2}}}{{{r_1}}}} \right)}}{{{l_1}}}\lambda }&{{l_{\rm{a}}} \in [L - {l_0} - {l_1},L - {l_0}]}\\ 1&{{l_{\rm{a}}} < L - {l_0} - {l_1}} \end{array}} \right.$ | (13) |
为了验证模型和计算方法的正确性,以LW550型变频钻井液离心机为例,并结合室内实验数据进行分析。离心机结构参数如表 1所示。
| 下载CSV 表 1 LW550离心机结构参数 Table 1 Structure parameters of the LW550 centrifuge |
采用固定变量法对加重钻井液进行分离实验,以粒径低于74 μm的重晶石粉捕集效率作为研究对象,通过实测值计算固相颗粒捕集效率。分别将相关参数带入文献中的捕集效率计算式(式(2))和本文提出的捕集效率计算式(式(13))中,将以上3组数据对比,从而验证本文捕集效率计算方法的正确性。
实验用钻井液中固相为膨润土和重晶石,具体参数如表 2所示。
| 下载CSV 表 2 钻井液参数 Table 2 Drilling fluid parameters |
在实验过程中,转速差控制在20~25 r/min。采用固定变量法,分别以转鼓转速、离心机处理量、重晶石粒径作为单一变量,钻井液含固量、底流含固量、溢流含固量、钻井液固相粒度微分分布、底流固相粒度微分分布作为测量值,进行3组实验,每组实验重复3次,实验结果取平均值。
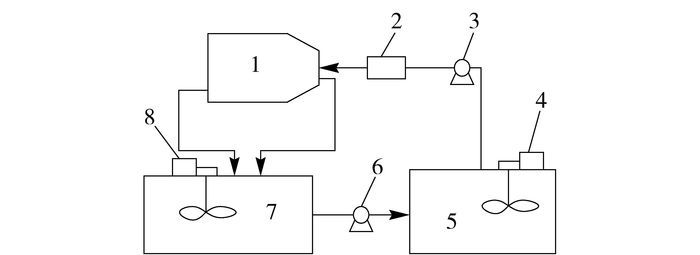
实验流程如图 3所示。将配好的加重泥浆放入储罐5中,待搅拌均匀后由泵送入钻井液离心机进行分离,调节流量控制阀控制离心机处理量,转鼓转速根据实验方案调节,待运行稳定后,在离心机进料口、底流口和溢流口分别取样,其余底流、溢流经管线流入储罐7,搅拌均匀后,由泵输送回储罐5,完成循环。3次取样后,调节转速,进行下一组实验。实验现场如图 4所示。
|
1—离心机;2—流量计;3,6—泵;4,8—泥浆搅拌器;5,7—储罐。 图 3 实验流程简图 Fig.3 The experiment flow diagram |

|
图 4 实验现场图 Fig.4 Photograph of the experimental apparatus |
将所有取样样品送至中石油西南油气田分公司勘探开发研究院开发实验室,使用ZNG-A型钻井液固相含量测定仪(郑州南北仪器设备有限公司)测得固相含量,从而计算出钻井液离心机分离效率;采用MS-MICRO PLUS激光粒度分析仪(英国马尔文仪器有限公司)测得颗粒粒径分布,从而计算出某粒径重晶石所占总固相的比值,进而得到该粒径重晶石捕集效率。捕集效率实测值计算公式为[9]
| ${E_{\rm{G}}} = \frac{{1 - \frac{{{C_{\rm{f}}}}}{{{C_0}}}}}{{1 - \frac{{{C_{\rm{f}}}}}{{{W_{\rm{f}}}}}}}\frac{{{f_{\rm{c}}}\left( {di} \right)}}{{f\left( {di} \right)}}$ | (14) |
通过实验可测得5个参数,分别为钻井液含固量、底流含固量、溢流含固量、钻井液固相粒度微分分布、底流固相粒度微分分布。对实验数据进行分析整理,代入公式(14) 得到不同转速下该粒径重晶石的捕集效率实测值。将表 1中离心机结构参数、表 2中钻井液参数以及每组实验的具体操作参数代入公式(2) 和公式(13) 中,分别得到采用文献方法的捕集效率理论计算值和本文捕集效率理论计算值。
(1) 取转鼓转速为自变量,步长为100 r/min,处理量为40 m3/h,以35 μm粒径重晶石捕集效率为研究对象。整理计算结果如表 3所示。
| 下载CSV 表 3 转速对捕集效率理论值和实验值的影响 Table 3 Comparison of calculated and experimental values of collection efficiency as a function of rotational speed |
由表 3可知,随着离心机转速等差递增,重晶石捕集效率的理论计算值和实验值均增大。这是由于随着转速的增加,颗粒受到的离心力增加,从而增大了沉降速度,导致颗粒沉降到转鼓壁的数量增加,这与工程上通过增大转速从而提高离心机的分离效果的经验相符。另一方面,采用本文捕集效率计算方法计算出的理论值和实验值的最大相对误差小于4%,远小于采用前人捕集效率计算式得到的结果,说明本文提出的理论计算方法具有一定的正确性和准确性。
(2) 取离心机处理量为自变量,步长为5 m3/h,转鼓转速为2000 r/min,以35 μm粒径重晶石的捕集效率为研究对象。整理计算结果如表 4所示。
| 下载CSV 表 4 处理量对捕集效率理论值和实验值的影响 Table 4 Comparison of calculated and experimental values of collection efficiency as a function of inlet flow flux |
由表 4可知,随着处理量的增加,重晶石捕集效率的理论值和实测值均减小。这是由于处理量的增大导致固相颗粒在离心机内的轴向运动速度增加,从而缩短了颗粒在离心机内停留的时间,使沉降到转鼓壁的颗粒数量减少。与采用前人捕集效率计算式得到的计算结果相比,采用本文方法的计算值与实测值之间的相对误差小于4%,说明了本文提出的理论方法的正确性。
(3) 取重晶石粒径为自变量,步长为2 μm,转鼓转速为2000 r/min,处理量为40 m3/h。计算结果如表 5所示。
| 下载CSV 表 5 粒径对捕集效率理论值和实验值的影响 Table 5 Comparison of calculated and experimental values of collection efficiency as a function of equivalent diameter |
由表 5可知,随着重晶石颗粒粒径的增大,离心机对该粒径颗粒捕集效率的理论值与实测值均增加。从理论上分析,颗粒越大受到的离心力越大,沉降速度也就越大,那么完成沉降的颗粒也就越多。采用本文捕集效率计算方法得到的理论值和实测值的相对误差小于4%,远低于采用前人研究方法计算出的捕集效率与实测值的相对误差,说明本文理论计算方法的正确性和准确性。
通过以上3组理论值和实测值的对比分析发现,随着自变量的变化,理论计算值与实测值的增减规律相同,且采用本文提出的捕集效率计算方法得到的理论值与实测值的相对误差均小于4%,说明本文提出的钻井液离心机捕集效率计算方法的正确性、准确性和实用性,也证明了本文提出的钻井液离心机沉降模型的正确。而所有实测值均小于理论计算值,则是由于理论计算中假设所有完成沉降的颗粒均被捕集,但在实际实验过程中,完成沉降的颗粒还要经过颗粒运移和脱水才能排出离心机,再加上离心机内流场中的漩涡、颗粒碰撞、湍流也会对离心机的捕集效率造成影响,从而造成了理论计算值和实测值的差异。
4 结论(1) 提出了新的钻井液离心机沉降模型,该模型针对钻井液离心机中布料口垂直于径向且转鼓内有螺旋推料器的结构特点而建立,充分考虑了初始沉降位置对离心机分离效果的影响。
(2) 推导得到了钻井液离心机固相颗粒捕集效率的计算公式,该公式描述了离心机结构参数、操作参数、钻井液参数和捕集效率之间的关系。
(3) 通过钻井液离心机室内实验,将文献中捕集效率理论计算值、本文所提方法计算值和实测值进行对比的结果表明:采用本文所提方法得到的理论值与实测值数据吻合度高,相对误差小于4%。说明本文提出的钻井液离心机沉降模型和捕集效率计算公式符合钻井液离心机的实际工作情况,可提高离心机捕集效率的理论计算精度。
符号说明
Vc—离心机内钻井液体积,m3
ut—Stokes沉降速度,m/s
Q—钻井液体积流量,m3/s
r1—溢流口距轴线距离,m
r2—转鼓内径,m
g—重力加速度,m/s2
dc—临界颗粒粒径,m
区域Ⅰ—沉降完成区
区域Ⅱ—沉降不能完成区
P—捕集效率理论计算值,%
uz—液相轴向速度,m/s
ur—颗粒干涉沉降速度,m/s
f(ε)—Richardson -Zaki方程
dx—固相颗粒当量直径m
l0—底流端初始沉降位置端点与柱段起点之间的距离,m
l1—初始沉降位置长度,m
l2—初始沉降位置中临界沉降起点靠底流端方向的长度,m
L—离心机柱段长度,m
SZ—颗粒最大轴向位移,m
la—给定参数条件下,某粒径颗粒沉降到转鼓壁轴向需要移动的距离,m
ω—转鼓角速度,rad/s
λ—效率因子,%
μ—黏度, Pa·s
ρs—固相密度, kg/m3
ρl—液相密度, kg/m3
ε—钻井液液相体积分数,%
EG—捕集效率实测值,%
C0—钻井液固相质量分数,%
Cf—溢流固相质量分数,%
Wf—底流固相质量分数,%
f(di)—直径为di的粒子,在钻井液固相的粒度微分分布中所占的分数
fc(di)—直径为di的粒子,在底流固相的粒度微分分布中所占的分数
| [1] |
Bybee K. An improved solids-control technique for onshore drilling in Trinidad[J]. Journal of Petroleum Technology, 2003, 23(11): 57-58. |
| [2] |
何宇. 钻井液高速离心机转鼓强度应力有限元分析与优化[J]. 石油矿场机械, 2012, 41(9): 46-49. He Y. High speed drilling fluid centrifuge drum strength finite element analysis and optimization[J]. Oil Field Equipment, 2012, 41(9): 46-49. (in Chinese) |
| [3] |
Bell G R A, Symons D D, Pearse J R. Mathematical model for solids transport power in a decanter centrifuge[J]. Chemical Engineering Science, 2014, 107: 114-122. DOI:10.1016/j.ces.2013.12.007 |
| [4] |
梁毅, 孙恒, 王东琪, 等. 卧螺离心机生产能力的FCPS理论[J]. 化工设备与管道, 2015, 51(1): 60-64. Liang Y, Sun H, Wang D Q, et al. FCPS theory for production capacity of decanter centrifuge[J]. Process Equipment & Piping, 2015, 51(1): 60-64. (in Chinese) |
| [5] |
钱健航, 龚卫红, 张春强. 石油钻井液专用卧螺离心机的研究[J]. 广东化工, 2012, 39(14): 151-152. Qian J H, Gong W H, Zhang C Q. Research on profession appropriation decanter centrifuges of the petroleum drilling fluid[J]. Guangdong Chemical Industry, 2012, 39(14): 151-152. (in Chinese) DOI:10.3969/j.issn.1007-1865.2012.14.075 |
| [6] |
Tan W, Qiao L, Sha E D, et al. Optimal design of the accelerator disk in a two-stage piston pusher centrifuge using numerical simulation[J]. Industrial & Engineering Chemistry Research, 2012, 51(30): 4632-4642. |
| [7] |
Rushton A, Ward A S, Holdich R G. Solid-liquid filtration and separation technology[M]. 2nd ed. New York, USA: Wiley-VCH, 2000: 295-308.
|
| [8] |
罗茜. 固液分离[M]. 北京: 冶金工业出版社, 1997: 95-99. Luo Q. Solid-liquid separation[M]. Beijing: Metallurgical Industry Press, 1997: 95-99. (in Chinese) |
| [9] |
孙启才, 金鼎五. 离心机原理结构与设计计算[M]. 北京: 机械工业出版社, 1987: 62-65. Sun Q C, Jin D W. Structure principle and design calculation of centrifuge[M]. Beijing: China Machine Press, 1987: 62-65. (in Chinese) |
| [10] |
Records A, Sutherland K. Decanter centrifuge handbook[M]. Oxford, UK:Elsevier Advanced Technology, 2001:1-2.
|
| [11] |
Zhu G R, Tan W, Yu Y, et al. Experimental and numerical study of the solid concentration distribution in a horizontal screw decanter centrifuge[J]. Industrial & Engineering Chemistry Research, 2013, 52(48): 17249-17256. |
| [12] |
付双成, 董连东, 袁惠新. 基于Euler多相流模型的卧螺离心机速度场数值模拟与分析[J]. 化工进展, 2014, 33(1): 36-42. Fu S C, Dong L D, Yuan H X. Numerical simulation and analysis on flow field in a decanter centrifuge based on the Euler model[J]. Chemical Industry and Engineering Progress, 2014, 33(1): 36-42. (in Chinese) DOI:10.3969/j.issn.1000-6613.2014.01.008 |
| [13] |
刘洪斌. 钻井液离心机工作理论研究[D]. 成都: 西南石油大学, 2006. Liu H B. Study on performance theory of drilling fluid centrifuge[D]. Chengdu:Southwest Petroleum University, 2006. (in Chinese) |
| [14] |
Svarovsky L. Solid-liquid separation[M]. 4th ed. Oxford, UK:Butterworth-Heinemann, 2000:150-200.
|








