2. 北京化工大学 教育部高分子材料加工装备工程研究中心, 北京 100029
2. Polymer Processing Equipment Engineering Research Center, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
微液滴喷射技术是近年来发展较快的高新技术之一,在自由成型、喷墨打印、流体点胶、生物医药及功能器件制造等方面均有重要的应用[1-3],尤其在自由成型领域,这一技术引起了国内外同行的广泛关注[4]。微液滴喷射自由成型的过程为:在某种外力的作用下,微喷头中的流体通过喷孔生成微小液滴,然后配合运动平台,微液滴逐层堆积为三维实体[5]。在这一过程中,研究微液滴在喷孔末端形成与断裂的过程对最终制品具有重要意义。对于微液滴的形成及断裂过程的研究由来已久[6],但鉴于这一过程的复杂性,至今尚未有完善的理论,目前仍是人们研究的重点。
微液滴形成及断裂过程的研究方法主要有实验法和数值模拟法。文献[7-8]在实验中通过高速摄像设备详细研究了水滴在毛细管末端形成及断裂的过程,然而实验方法成本较高,且仅能观测微液滴外在形态的变化,不能揭示内在规律。随着数值计算理论及计算机技术的发展,人们越来越多选择数值模拟方法来研究这一过程。文献[9]利用有限元方法计算出水滴的颈缩线等微观特性,较为精确地预测到水滴形态的变化;文献[10]利用流体力学软件模拟了石蜡液滴形成过程的速度场及温度场,并得出其变化规律。
以上文献在研究中所使用流体均为黏度小于30 mPa·s的低黏度流体,而对具有高黏性的高聚物熔体微液滴研究较少。本文利用数值模拟方法,借助计算流体力学软件Fluent研究了聚丙烯熔体微液滴的形成与断裂过程,并着重分析了微喷头结构参数对熔滴体积的影响。
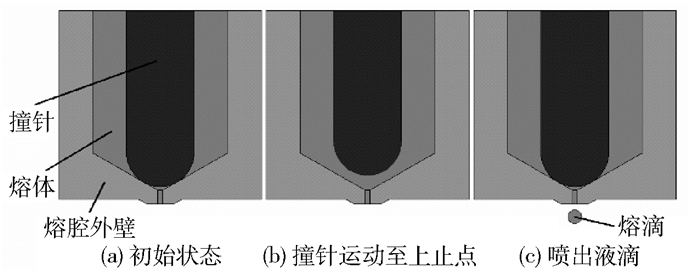
1 机械式微喷头工作原理根据驱动外力的不同,产生熔体微液滴有机械式、气压式、压电式、电磁式等多种方式[2]。本文采用机械式微喷头来产生熔体微液滴,其工作原理如图 1所示。图 1(a)为初始状态,撞针位于下止点,与喷嘴斜面紧密贴合,熔体不能从喷孔中喷出;然后撞针运动到上止点,如图 1(b)所示,熔体在熔压作用下填补由于撞针运动而产生的空隙;接着撞针又运动至下止点,如图 1(c)所示,熔体在撞针的挤压作用下产生一微小熔滴从喷孔中喷出。以上过程为机械撞针式微喷头的一个工作循环,如此循环往复,就可以根据需要产生连续熔滴。本文主要模拟了撞针从上止点运动至下止点后,熔滴在喷孔末端形成并断裂的过程。
|
图 1 机械撞针式喷头 Fig.1 Mechanical jet |
高聚物熔体微液滴形成及断裂的过程是一个复杂的流体动力学问题,为了使问题易于求解,本文作如下假设和简化:① 由于模拟用聚丙烯熔体弹性微弱,黏度随温度及剪切速率变化较小,因此可假设其是黏度为常数的不可压缩牛顿流体;② 由于熔体区域和空气区域加热温度一致,且气体流速较低,可认为空气相与熔体相间只存在动量传递,不涉及传热问题;③ 喷射熔滴体积极微小,可不考虑重力的影响;④ 所研究问题轴对称,计算区域取经过对称轴的任意一个面。
基于上述假设简化及相关流体力学知识,可得到柱坐标形式下的流动控制基本方程组。
质量守恒方程为
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial r}} = 0 $ | (1) |
动量方程为
| $ {\frac{{\partial \left( {\rho u} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho u\boldsymbol{U}} \right) = {\rm{div}}\left( {\mu {\rm{grad}}u} \right) - \frac{{\partial p}}{{\partial x}} - \rho g} $ | (2) |
| $ {\frac{{\partial \left( {\rho v} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho v\boldsymbol{U}} \right) = {\rm{div}}\left( {\mu {\rm{grad}}v} \right) - \frac{{\partial p}}{{\partial r}}} $ | (3) |
式中,u、v分别为速度矢量U在轴向x及径向r方向上的分量,ρ为密度,μ为黏度,p为压力,g为重力加速度。
微液滴喷射及断裂过程属于气液两相流问题,本文选用volume of fluid(VOF)方法追踪气液间自由运动界面,附加方程为两相流的体积分数方程:
| $ \frac{{\partial C}}{{\partial t}} + \boldsymbol{V}{\rm{grad}}C = 0{\rm{ }} $ | (4) |
其中,C为网格单元内熔体相的体积分数, V为熔体的速度。
可以看出,式(1)~(4) 流体控制方程组是非线性的偏微分方程组,且熔体微液滴形成与断裂过程中的边界条件较为复杂,因此求取方程的解析解是不可能的。商业计算流体力学软件Fluent利用有限体积法来离散上述控制方程组,通过数值计算最终可以求得流场的数值解。
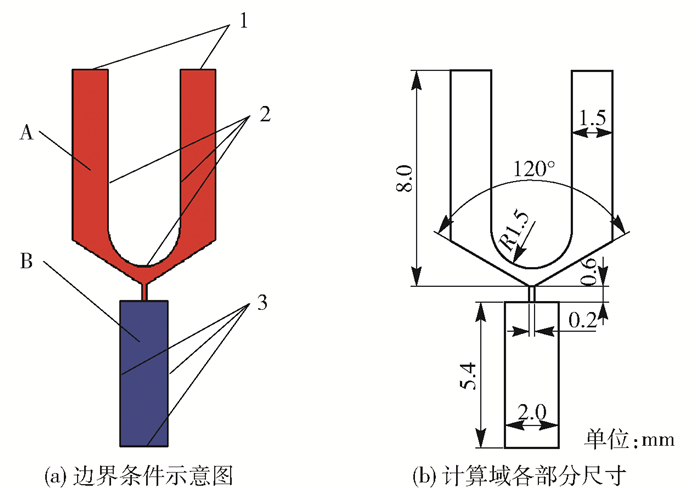
3 计算模型及边界初值条件由于所求问题为非稳态问题,先运用前处理软件Gambit建立二维初始流体计算域模型并对其划分网格,再利用Fluent软件设置动网格等参数,初始计算模型及相关尺寸如图 2所示。图 2(a)中1为压力进口,设定为熔体供料压力;2为撞针运动边界,在实际的喷头中,撞针的运动比较复杂,难以求取其准确的运动轨迹,但由于撞针的运动位移较短,本文的仿真将其视为匀速运动,初始状态下撞针位于上止点,撞针的运动使用user defined funceion(UDF)函数编写;3为压力出口,设定为大气压力;区域A表示熔体腔,初始状态下充满高聚物熔体;区域B是液滴自由运动区域,初始状态下充满空气;其余未编号边界为固壁无滑移边界条件。
|
1—压力进口;2—撞针运动边界;3—压力出口。 图 2 初始计算域 Fig.2 Initial calculation model |
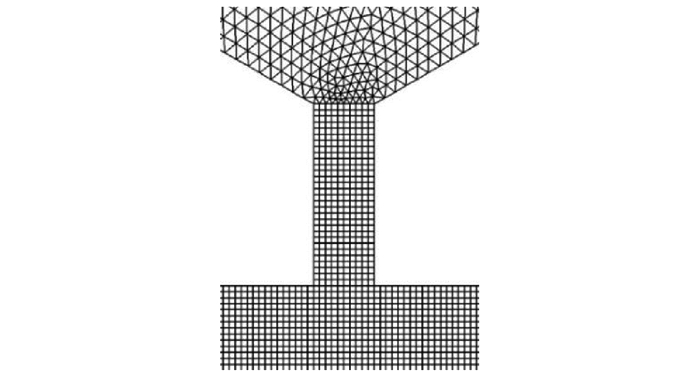
考虑到Fluent软件计算精度和计算效率的需要,本文将熔腔部分划分为三角形网格,而将喷孔及液滴自由运动区域划分为结构化四边形网格,总网格单元数为31466,图 3为喷孔处及其附近网格细节示意图。
|
图 3 喷孔处网格划分 Fig.3 Meshing of the orifice |
本文的模拟属于瞬态数值模拟,因此需要确定数值计算所采用的网格数量及时间步长与最终结果的无关性,即进行网格无关性和时间步长独立性验证。采用Fluent14.5进行模拟,取60 μs时喷孔出口中心点处的速度值作为验证数据,结果如表 1和表 2所示。可以看到,随着网格数量的增加及时间步长的减小,速度值变化极微小,可以近似认为速度达到稳定。为节省计算成本,提高效率,经综合考虑,本文将网格数量取为31466,时间步长取为1 μs。
| 下载CSV 表 1 网格独立性验证 Table 1 Mesh independence verification |
| 下载CSV 表 2 时间步长无关性验证 Table 2 Step time independence verification |
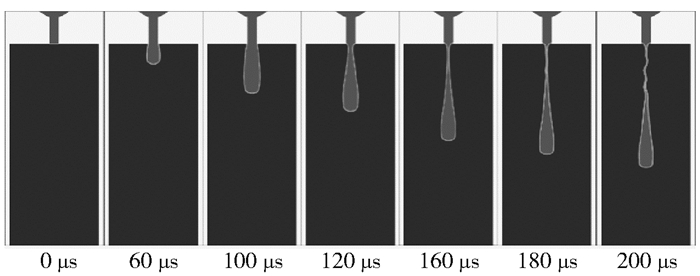
为了探究高聚物熔体微液滴形成及断裂的机理,本文通过模拟得到的体积分数云图如图 4所示。为了便于观察及叙述,体积分数云图仅截取了喷孔及液滴自由运动区域的部分,熔体腔区域未示出。设定的工艺条件及物性参数如表 3所示。结合图 4,通过分析流场的数值解来定性分析熔体微液滴形成与断裂的机理。
|
图 4 体积分数云图 Fig.4 Contours of volume fraction |
| 下载CSV 表 3 工艺条件及物性参数 Table 3 Condition settings |
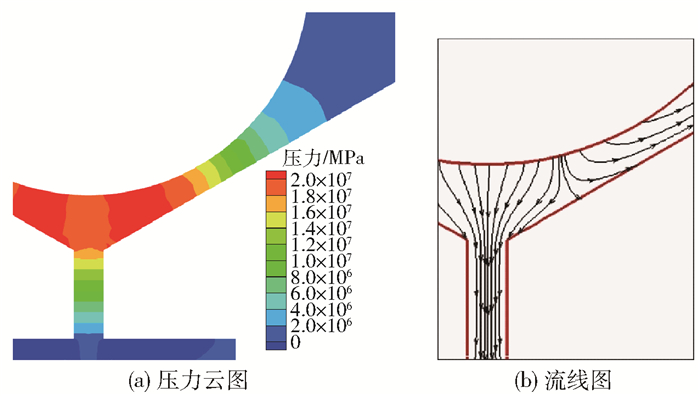
图 4中,0 μs为初始状态,然后撞针以一定速度向下运动撞击熔体,使熔体以一束流体的形式从喷孔中喷出。60 μs为撞针运动一段距离后的情形,束状流体由于表面张力及空气阻力的作用呈一定的椭球状,图 5(a)所示为此刻熔体腔内的压力云图。从图中可以看出,由于撞针的高速运动,在撞针端部及喷嘴锥面所围成的区域中形成了较高的局部压力,其值可达20 MPa,在这一压力作用下,局部高压区的熔体出现分流,一部分熔体经过喷孔喷出形成束状流体,而另一部分熔体向上运动流向压力较低的进口区域,图 5(b)为此刻熔腔内熔体运动的流线图。熔体两种流向的大小决定了微喷头单次喷射所能喷射的熔滴体积。
|
图 5 60 μs时熔腔内压力云图及流线图 Fig.5 Pressure contours and streamline of the chamber at 60 μs |
100 μs时,撞针恰好运动到下止点,由于撞针将喷嘴封堵,熔腔中的熔体不再向下喷出,此刻束状流体的体积基本等于单次喷射液滴的体积。此时对束状流体做受力分析,其受到惯性力、黏滞阻力、表面张力、空气阻力及重力的综合作用。然而对于本文模拟所用高聚物熔体来说,黏滞阻力的作用要远大于表面张力的影响,因此可以忽略表面张力的作用;而重力和空气阻力的作用又比较小,因此束状流体在形成液滴的过程中主要受到向下的惯性力及向上的粘滞阻力的作用,一束流体能否断裂成滴,就取决于这两个力的大小。如若惯性力大于粘滞力的作用,则可以断裂成滴;反之,则不能。在惯性力及粘滞力的共同作用下,液滴的上部发生颈缩,如120 μs(图 4,下同)时所示;随着颈缩进一步加强,颈缩处形成一条细长液线,如160 μs时所示;然后液线被不断拉长变细,直至变得不稳定,如180 μs和200 μs时所示,此时可以认为液滴已经发生断裂。
5 结果与讨论 5.1 物性参数对熔滴形态的影响在实际应用中,熔滴在喷射过程中的形态具有重要的研究意义。影响熔滴形态的参数主要包括熔体的表面张力和黏滞阻力。表面张力作用于熔体和气体的边界,促使熔滴收缩成球,而黏滞阻力会阻碍熔滴的收缩。图 6所示为有人用高速摄像机拍摄到的水滴的形成过程[11]。从图中可以看出,和4.2节模拟结果类似,水滴的形成也要经历颈缩、伸长及断裂等过程,然而水滴和熔体液滴的形态却有很大的差别,这是由两者的黏度差别造成的。水在常温下的黏度约为1 mPa·s,而模拟用高聚物熔体黏度为5000 mPa·s,两者相差3个数量级。由于黏度较低,水滴形成时表面张力的作用大于黏滞阻力的作用,水滴在表面张力的作用下会收缩为几乎标准的球形;而高聚物熔滴形成过程中,黏滞力远大于表面张力,熔滴难以收缩为球形,而呈现为拖尾状。

|
图 6 水滴形成过程 Fig.6 Formation of a water-drop |
为了探究表面张力的影响,本文模拟了表面张力系数分别为0.02、0.2、2 N/m下,熔滴断裂时刻的情形,如图 7所示。从图中可以看出,随着表面张力系数的增大,熔滴表面略显圆润,但熔滴仍有较长拖尾,形态变化微小。而在实际运用中,聚丙烯熔体的表面张力系数变化范围很小,远不能达到本文模拟所设定的范围,这再一次证明了在高黏度流体微液滴喷射过程中,表面张力的影响可以忽略不计。

|
图 7 不同表面张力下的熔滴形态 Fig.7 Droplet shapes for different values of surface tension |
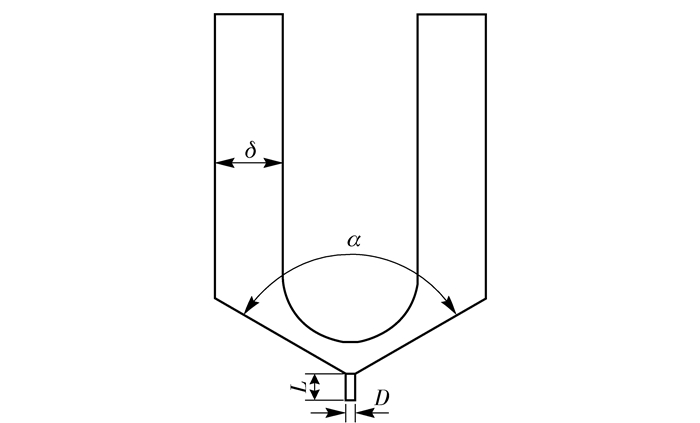
在高聚物熔体微液滴喷射自由成型过程中,熔滴体积是决定成型制件表面质量的关键因素,熔滴体积越小,成型制件表面越光滑;反之,则越粗糙。如何获取更小的熔滴体积一直是研究者重点关注的问题。熔滴体积受诸多因素的影响,对于机械撞针式微滴喷射工艺来说,主要影响因素有结构参数、工艺参数及物性参数。本文主要讨论锥面张角α、熔腔间隙δ、喷孔直径D、喷孔长度L等4个结构参数对熔滴体积的影响(图 8)。
|
图 8 结构参数 Fig.8 Structural parameters |
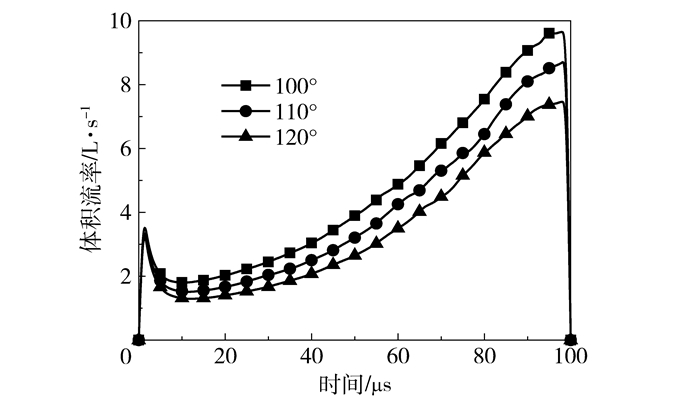
在原模型的基础上,分别对锥面张角为100°、110°及120°时的情况进行了模拟,得到了喷孔出口处体积流率随时间的变化曲线(图 9)。体积流率虽不能准确反映所喷射液滴的体积,但从中可以直观地看到体积随结构参数的变化规律。可以看出,随着撞针从上止点开始运行,体积流率先是急剧上升,而后又有轻微下降,接着又缓慢上升到最大,最后在撞针运行到下止点那一刻迅速降为零。另外可以看到,随着喷嘴张角的增大,所喷射的熔滴体积逐渐减小,这是因为锥面张角越大,撞针末端在挤压熔体时,熔体更容易流向压力较低的进口,而不是流向压力较高的喷孔。虽然大的锥面张角可以获得较小的熔滴,但不利于局部高压的建立,进而使得熔体获得的惯性力较小,熔滴不易断裂,因此在保证熔滴可以正常断裂的情况下,应选较大的锥面张角。
|
图 9 不同锥面张角下的体积流率 Fig.9 Volume flow rates for different cone angles |
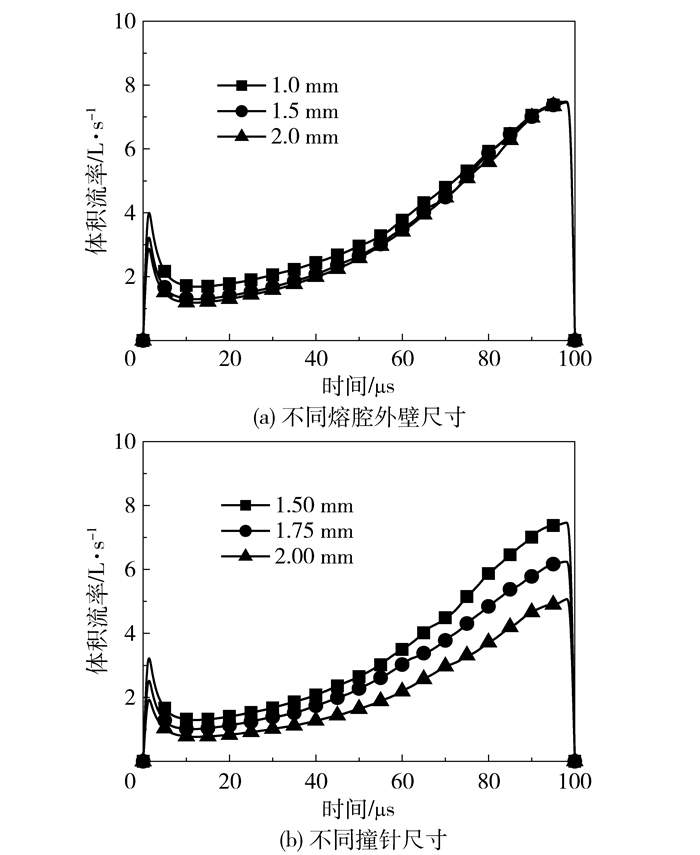
在原模型基础上,可以通过两种方式改变熔腔间隙:第一种是保持撞针尺寸不变,增大熔腔外壁尺寸;第二种是保持熔腔外壁尺寸不变,减小撞针尺寸。图 10(a)为在第一种情况下改变熔腔间隙得到的体积流率随时间的变化关系;图 10(b)为在第二种情况下改变熔腔间隙得到的体积流率随时间的变化关系。由图可知,总体上,熔腔间隙越大,越有助于形成较小的熔滴。但在第一种情况下,熔滴体积随熔腔间隙的变化并不是很显著,这是因为增大熔腔外壁尺寸并不能影响撞针末端与锥面所构成的局部高压熔腔,因而对此区域熔体的流向影响较小;而在第二种情况下,改变撞针尺寸会显著减小局部高压熔腔,因此可以喷射较小熔滴。
|
图 10 不同熔腔间隙下的体积流率 Fig.10 Volume flow rates for different chamber gaps |
图 11所示为在原模型基础上改变喷孔直径及喷孔长度后体积流率随时间的变化。从图中可以得知,随着长径比的增大,喷射的熔滴体积随之变小,即细长喷孔有利于得到微小熔滴。这是因为细长喷孔阻力较大,在撞针的撞击作用下会迫使更多的熔体流向阻力较小的进口处;另外细长喷孔也有利于局部高压的建立,因而所喷射的熔滴可以获得较大的惯性力,有利于液滴的断裂。因此在加工条件允许的情况下,应设计具有细长喷孔的微喷头。
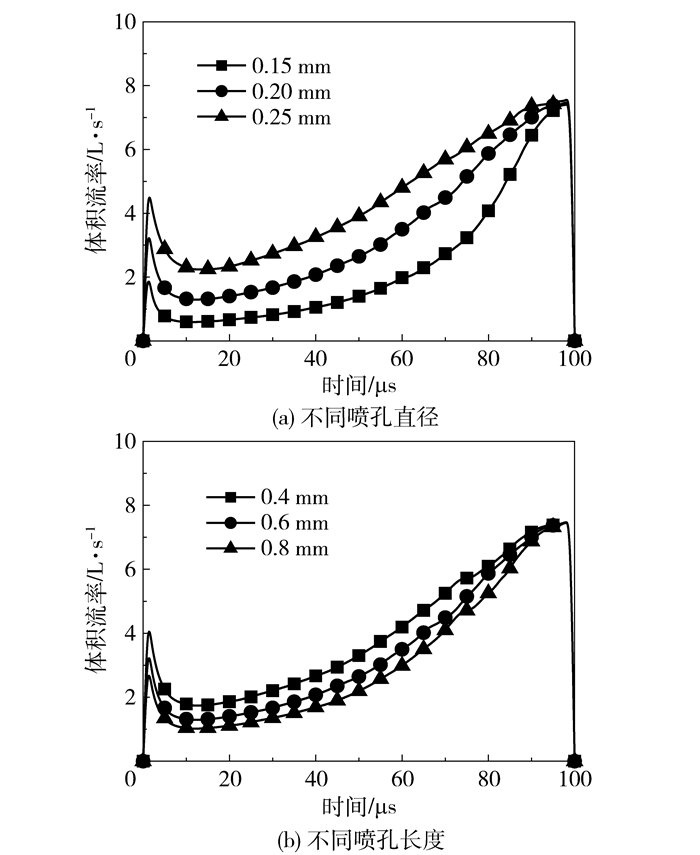
|
图 11 不同喷孔尺寸下的体积流率 Fig.11 Volume flow rates for different orifice dimensions |
(1) 一束流体在喷孔末端形成微熔滴的过程中要经历颈缩、伸长以及断裂等过程,熔滴能否形成取决于其获得的惯性力能否克服黏滞阻力的作用。
(2) 高黏度的聚合物微滴在形成过程中的形态与水滴等低黏度微液滴有显著差别,究其原因是黏度的巨大差异导致表面张力的作用效果不同。
(3) 在可以实现正常喷射的条件下,锥面张角越大、熔腔间隙越大、喷孔越细长,则有利于获得更小的微熔滴。
| [1] |
吴任东, 魏大忠, 周浩颖, 等. 三维数字微滴喷射成形技术的发展现状[J]. 新技术新工艺, 2004(2): 35-38. Wu R D, Wei D Z, Zhou H Y, et al. The development of 3D digital micro-droplet jetting forming[J]. New Technology & New Process, 2004(2): 35-38. (in Chinese) |
| [2] |
罗志伟, 赵小双, 罗莹莹, 等. 微滴喷射技术的研究现状及应用[J]. 重庆理工大学学报:自然科学版, 2015, 29(5): 27-32. Luo Z W, Zhao X S, Luo Y Y, et al. Application and research status of droplet jetting technique[J]. Journal of Chongqing University of Technology:Natural Science, 2015, 29(5): 27-32. (in Chinese) |
| [3] |
Singh M, Haverinen H M, Dhagat P, et al. Inkjet printing-process and its applications[J]. Advanced Materials, 2010, 22(6): 673-685. DOI:10.1002/adma.v22:6 |
| [4] |
Luo J, Qi L H, Jiang X S, et al. Research on lateral instability of the uniform-charged droplet stream during droplet-based freeform fabrication[J]. International Journal of Machine Tools & Manufacture, 2008, 48(3): 289-294. |
| [5] |
杨来侠, 陈龙. 液滴喷射过程流场与速度场的数值模拟[J]. 机械设计与制造, 2015(1): 105-108. Yang L X, Chen L. Numerical simulation of flow field and velocity field for droplet jetting process[J]. Machinery Design & Manufacture, 2015(1): 105-108. (in Chinese) |
| [6] |
Eggers J. Theory of drop formation[J]. Physics of Fluids, 1995, 7(5): 941-953. DOI:10.1063/1.868570 |
| [7] |
Brenner M P, Eggers J, Joseph K, et al. Breakdown of scaling in droplet fission at high Reynolds number[J]. Physics of Fluids, 1997, 9(6): 1573-1590. DOI:10.1063/1.869279 |
| [8] |
Kowalewski T A. On the separation of droplets from a liquid jet[J]. Fluid Dynamics Research, 1996, 17(3): 121-145. DOI:10.1016/0169-5983(95)00028-3 |
| [9] |
Ambravaneswaran B, Wilkes E D, Basaran O A. Drop formation from a capillary tube:comparison of one-dimensional and two-dimensional analyses and occurrence of satellite drops[J]. Physics of Fluids, 2002, 14(8): 2606-2621. DOI:10.1063/1.1485077 |
| [10] |
齐乐华, 罗俊, 李莉, 等. 均匀液滴喷射过程仿真与试验研究[J]. 机械工程学报, 2008, 44(12): 86-92. Qi L H, Luo J, Li L, et al. Simulation and experimental research of the uniform droplet spray process[J]. Chinese Journal of Mechanical Engineering, 2008, 44(12): 86-92. (in Chinese) |
| [11] |
Henderson D M, Pritchard W G, Smolka L B. On the pinch-off of a pendant drop of viscous fluid[J]. Physics of Fluids, 1997, 9(11): 3188-3200. DOI:10.1063/1.869435 |








