降膜蒸发器是一种传统高效的蒸发设备,具有温差小、滞留时间短、工作寿命长和效率系数不受限制等优点,目前已应用于制冷、化工、石油和海水淡化等领域[1]。在竖直管降膜蒸发器中,换热管内向下流动的液膜与换热管外热介质间发生热交换,液膜受热蒸发而汽化[2]。但是换热管内表面或各换热管间液体分布不均容易导致换热管结垢,进而降低降膜蒸发器的换热强度[3]。
布膜技术是降膜蒸发器的核心技术之一[1],换热管表面稳定均匀的液膜是有效传热的前提。布膜器的作用是使料液均匀地分布到换热管中,并沿换热管内壁形成自上而下的膜状流动[4]。布膜器种类繁多,结构各异[5],其结构设计的合理性直接决定了液体成膜的均匀性。
某公司竖直管降膜蒸发器换热效果差,不能满足生产需求,分析发现该蒸发器采用径向进液布膜器而不是切向进液溢流孔式布膜器。本文基于真实布膜器尺寸,利用Fluent软件对影响当前竖直管降膜蒸发器换热效果的布膜器结构、溢流孔上方液位高度进行了数值模拟计算,并确定布膜器的最优液位高度。
1 布膜器结构及其工作原理溢流型布膜器分孔式和槽式两种,具有结构简单,加工、安装精度高,操作弹性大等优点。其工作原理是在换热管上部沿管壁切线方向开孔或者开槽[3],流体依靠管板上部液位高度H静压流下,结构如图 1所示。考虑到加工误差以及堵塞等问题,文献[3]中小孔直径或槽宽取2~3 mm,数量3~4个。
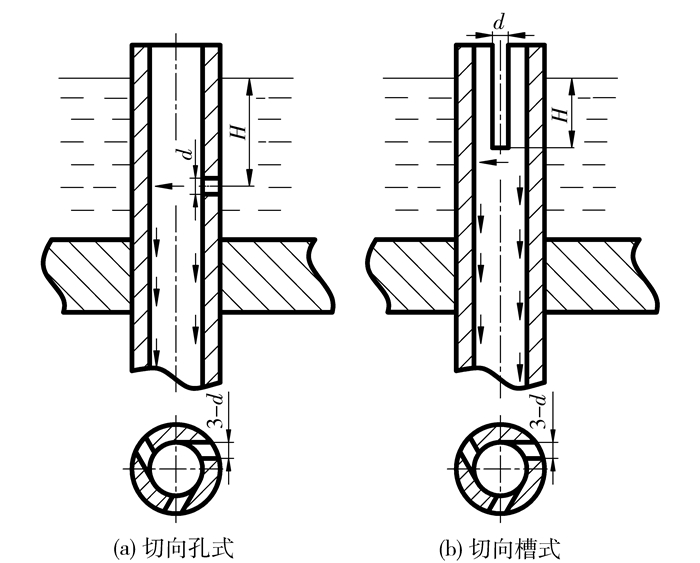
|
图 1 溢流型布膜器结构 Fig.1 The structure of overflow type distributors |
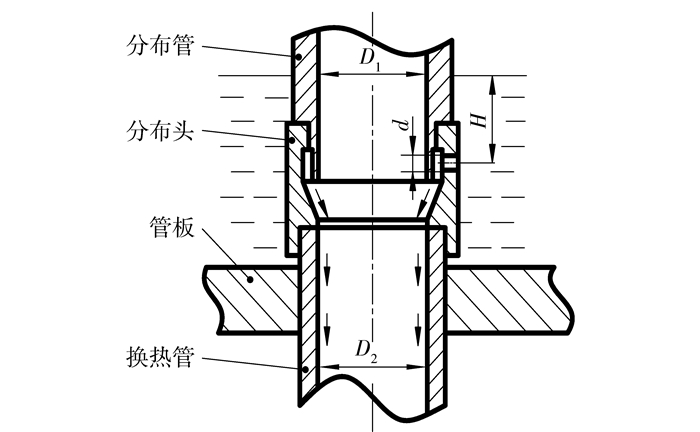
|
图 2 溢流孔式布膜器结构图 Fig.2 Structure chart of overflow hole type liquid distributor |
| 下载CSV 表 1 模型结构参数 Table 1 Model size |
关于液膜厚度σ,存在如下关系[3]
| $ \sigma \propto AR{e^x}{\upsilon ^y}{\left( {\frac{1}{g}} \right)^z} $ | (1) |
式中:x、y、z均为正数;A>0,为常数;Re为管内雷诺数;υ为液体运动黏度,m2/s;g为重力加速度,m/s2。
管内雷诺数Re由式(2) 计算:
| $ Re = \frac{q}{{\pi d\nu }} $ | (2) |
式中,q为每根换热管中的体积流量,m3/s;d为换热管内径,m;ν为液体运动黏度,m2/s。
切向孔式布膜器的流量q由式(3) 计算[3]
| $ q = CF\sqrt {2gH} $ | (3) |
式中,C为流量系数,一般取0.6~0.75;F为孔道总面积,m2;H为小孔中心上方液位高度,m;g为重力加速度,m/s2。
在流体种类和布膜器结构一定的条件下,由式(1)、(2) 可知,液膜厚度只与换热管中流量成正比;由式(3) 得出,此时流量仅与溢流孔中心液位高度成正比,即液膜厚度仅与溢流孔上方液位高度成正比。
2 模型方法的选择 2.1 模型选择求解器采用三维压力基隐式求解器,湍流模型选择标准k-ε方程模型,多相流模型选择volume of fluid(VOF)模型,操作介质采用水与空气。
布膜器内部流场连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\rho u} \right) + \frac{\partial }{{\partial y}}\left( {\rho v} \right) + \frac{\partial }{{\partial z}}\left( {\rho w} \right) = 0 $ | (4) |
式中,ρ为流体密度,t为时间,u为速度的x方向分量,v为速度的y方向分量,w为速度的z方向分量。
标准k-ε方程模型适用于高雷诺数的湍流计算模型,主要基于湍流动能和扩散率。
湍流动能方程—k方程:
| $ \rho \frac{{Dk}}{{Dt}} = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {{\mu _{\rm{l}}} + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _{\rm{k}}}}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right] + {G_{\rm{k}}} + {G_{\rm{b}}} - \rho \varepsilon $ | (5) |
式中,k为湍流动能;μl为层流黏性系数;μt为湍流黏性系数;σk为经验常数,Fluent软件一般取值1.0;Gk为由平均速度梯度产生的湍流动能;Gb是由浮力产生的湍流动能;ε为湍流扩散率。
湍流扩散率方程—ε方程:
| $ \rho \frac{{D\varepsilon }}{{Dt}} = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + {C_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{G_{\rm{k}}} + {C_{3\varepsilon }}{G_{\rm{b}}}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} $ | (6) |
| $ \mu = {\mu _{\rm{t}}} + {\mu _{\rm{l}}} $ | (7) |
式中,μ为有效黏性系数;σε,C1ε,C2ε,C3ε为经验常数。
VOF模型主要应用于分层流、自由液面流动等情况,可以计算流动过程中分界面的时空分布[6]。
2.2 网格划分采用蜂窝状多面体网格单元进行网格划分(图 3),其特点是在保证精度的前提下,有效减少总网格数,提高计算效率[7]。
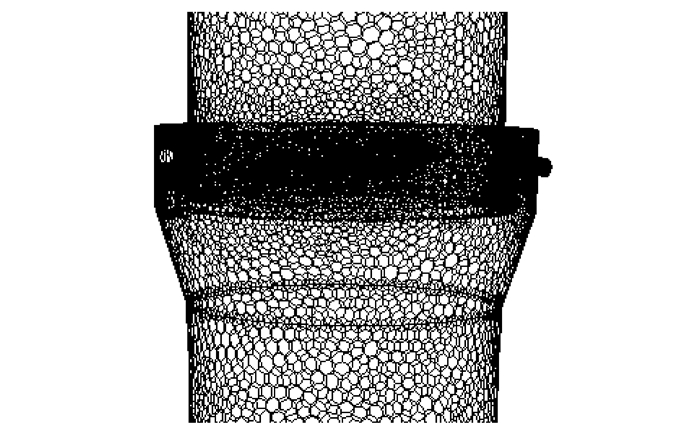
|
图 3 蜂窝状网格划分 Fig.3 Cellular structure grid |
采用压力入口边界,入口液相体积分数为1,压力值-56570 Pa,为液位静压与管程操作压力之和;出口边界采用压力出口,压力值-60000 Pa,为管程操作压力;壁面边界为无滑移固定壁面,默认壁面粗糙度0.5;初始化时将流体域充满空气。
3 结果与讨论 3.1 网格无关性检验对切向入口模型划分不同数量的网格,计算结果至收敛。定义液体从分布头进入换热管的横截面为Z=0截面。图 4为Z=0截面上同一位置的液相体积分数α,由图可知当网格数量变化时,曲线重合度较高,认为80万网格已达到网格无关,故取80万的网格作为计算网格。
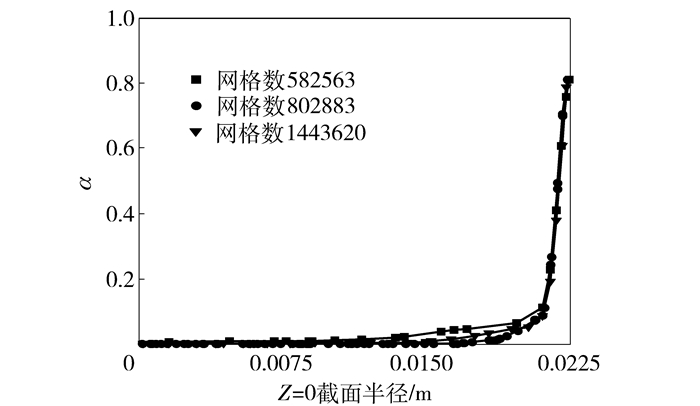
|
图 4 网格无关性验证结果 Fig.4 Grid independence test result |
Fluent计算收敛后,二者迹线如图 5所示。
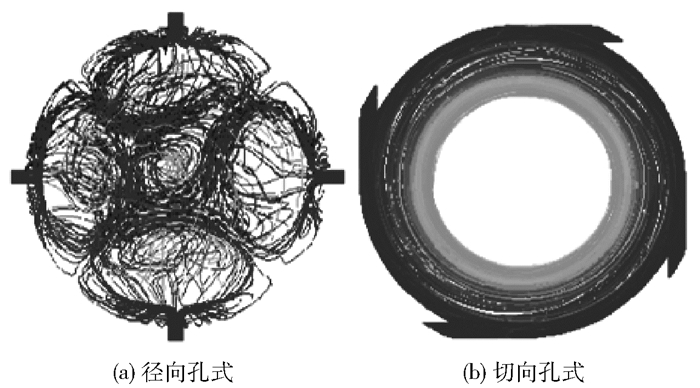
|
图 5 流体迹线图对比 Fig.5 Comparison of fluid pathline |
可以看出,在径向孔式布膜器中,流体首先撞击到分布管,然后分散向两侧及下方流动,与相邻入口分散到两侧的流体发生汇聚,然后流向换热管中心部位,只有部分流体沿壁面向下流动;切向孔式布膜器,流体进入换热管后,在分布管的束缚下,经分布头能很好地沿壁面流动。图 6所示的Z=0截面上液相体积分数云图与图 5所示液体迹线分布规律相符。

|
图 6 Z=0截面液相体积分数云图 Fig.6 Liquid volume fraction contours in the plane Z=0 |
对比二者相同位置的速度分布,如图 7所示,径向孔式布膜器在换热管壁面至中心轴线处,有两次流速增加过程:第一次与切向孔式布膜器原因相同,是流体在近壁面处流速为零,远离壁面流速增加的体现;第二次是由于部分流体未沿壁面流下,直接进入换热管中心区域造成。这与流体迹线图 5的分析结论一致。
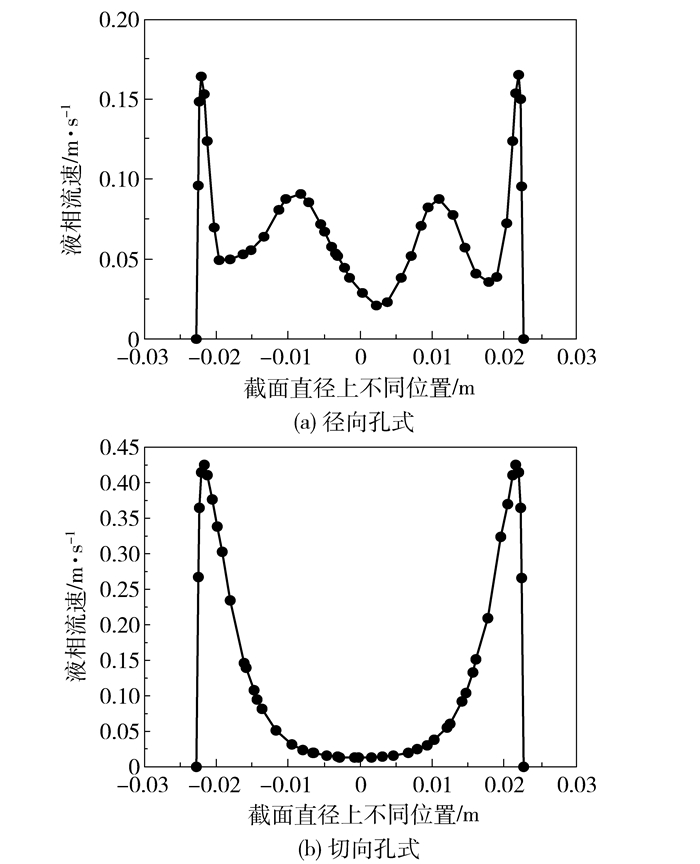
|
图 7 Z=0截面相同位置速度分布 Fig.7 Velocity distributions at the same location in the plane Z=0 |
对于溢流孔式布膜器,液位高度H影响降液流率,与成膜效果息息相关,存在临界值。当液位高度小于临界值,流体呈线性流下,不能形成液膜;液位高度H满足临界值要求,均匀液膜的形成远离换热管入口,换热管能够进行高效换热的有效长度缩短,换热管入口段换热面积利用率下降,降低传热效果;液位高度H过大,会增加设备的制造成本。确定合理的入口上方液位高度H非常关键。
基于CFD模拟计算,截面Z=0周向不同角度半径上OA(0°)、OB(45°)、OC(90°)、OD(135°)的液相体积分数的差异可判断成膜效果。当流体在换热管壁面能很好地成膜时,液相体积分数在周向壁面上不同角度的分布一致性较高,差值小。
如图 8所示,H=30 mm时,Z=0截面壁面尚未均匀成膜,此时不同角度壁面上液相体积分数差异大,最大差值约0.13(图 9)。
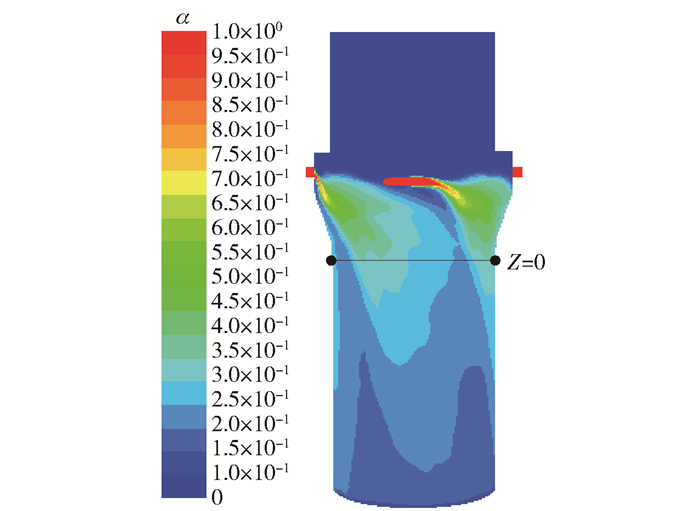
|
图 8 H=30 mm液相体积分数云图 Fig.8 Liquid volume fraction contours with a liquid level of 30 mm |
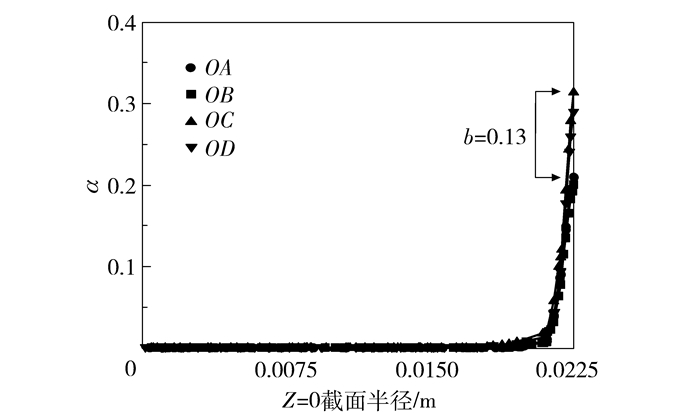
|
b—液相体积分数最大差值。 图 9 H=30 mm液相体积分数分布图 Fig.9 Liquid volume fraction distribution with a liquid level of 30 mm |
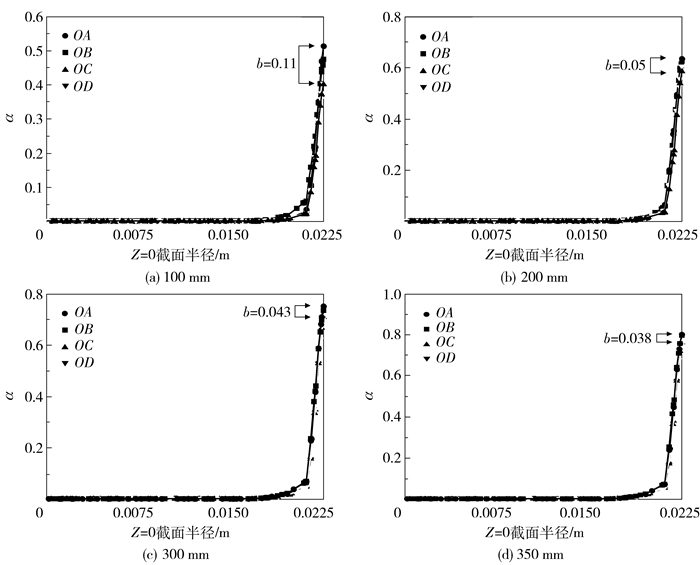
如图 10所示,液位高度从100 mm增至350 mm,液相体积分数最大差值从约0.11降至约0.038,此时曲线重合良好,液相体积分数云图如图 6所示,成膜效果良好。
|
b—液相体积分数最大差值。 图 10 液位高度对成膜影响 Fig.10 The influence of the liquid level in film-forming |
选用有机玻璃,按图 2和表 1加工制做布膜器,搭建布膜器成膜效果实验装置如图 11所示,进行单管冷模实验,实验介质为水。

|
图 11 实验装置实物图 Fig.11 Photograph of the experimental facility |
为减小进液流体的冲击作用,采用逐级溢流的方式使液体进入布膜器内部。
如图 12所示,实验布膜器入口上方液位高度达到350 mm时,径向孔进液布膜器的换热管壁面无法均匀成膜,布膜效果不理想;切向孔进液布膜器的换热管内壁面布满流体,成膜效果良好。实验结论与Fluent数值模拟结论一致。

|
图 12 成膜效果对比图 Fig.12 Comparison of film-forming effects |
改变切向孔进液布膜器的H值,观察换热管内壁面成膜情况。当H从500 mm逐渐降低至280 mm时,换热管出口处流体薄膜消失,流体分股流下,内壁面液膜波动明显(图 13)。

|
图 13 切向孔成膜效果图 Fig.13 Photograph of film-forming with tangential holes |
(1) 相较于切向孔进液方式,溢流型径向孔布膜器成膜效果差,不宜用作竖直管降膜蒸发器布膜器。
(2) 溢流型布膜器上方的液位高度H影响布膜效果,在给定条件下控制液位高度H不小于300 mm能保证良好的布膜效果。
| [1] |
张猛, 周帼彦, 朱冬生. 降膜蒸发器的研究进展[J]. 流体机械, 2012, 40(6): 82-86. Zhang M, Zhou G Y, Zhu D S. Research progress of falling-film evaporator[J]. Fluid Machinery, 2012, 40(6): 82-86. (in Chinese) |
| [2] |
朱玉峰. 竖管降膜蒸发器分布器的实验研究[J]. 河北科技大学学报, 2010, 31(3): 256-259. Zhu Y F. Experiment study on distributor of vertical tube falling-film evaporator[J]. Journal of Hebei University of Science and Technology, 2010, 31(3): 256-259. (in Chinese) DOI:10.7535/hbkd.2010yx03016 |
| [3] |
史晓平, 胡修慈. 竖管降膜蒸发器的布料装置[J]. 化学工程, 1990, 18(4): 14-18. Shi X P, Hu X C. Distributor of vertical tube falling film evaporator[J]. Chemical Engineering, 1990, 18(4): 14-18. (in Chinese) |
| [4] |
王根立. 降膜蒸发器布膜器的设计[J]. 化工装备技术, 2016, 37(1): 6-9. Wang G L. Design of film distributor in falling-film evaporator[J]. Chemical Equipment Technology, 2016, 37(1): 6-9. (in Chinese) |
| [5] |
高国华, 李研, 赵继文, 等. 直管预分布管的CFD模拟研究及变径设计[J]. 化工进展, 2009, 28(增刊): 355-359. Gao G H, Li Y, Zhao J W, et al. CFD simulation study and reducing design of straight tube pre-distributor[J]. Chemical Industry and Engineering Progress, 2009, 28(Suppl): 355-359. (in Chinese) |
| [6] |
胡坤. ANSYS ICEM CFD工程实例详解[M]. 北京: 人民邮电出版社, 2014. Hu K. ANSYS ICEM CFD Engineering example details[M]. Beijing: Posts and Telecom Press, 2014. (in Chinese) |
| [7] |
李成兵, 熊琎. 新型柱式气液旋流分离器数值计算[J]. 石油矿场机械, 2011, 40(2): 34-37. Li C B, Xiong J. Numerical calculation of new type gas-liquid cylindrical cyclone[J]. Oil Field Equipment, 2011, 40(2): 34-37. (in Chinese) |








