旋转机械在诸多领域的实际生产中都扮演着重要的角色,而转子的不平衡作为旋转机械最主要的激振源,是影响旋转机械能否平稳运行的关键因素。若采用传统现场动平衡方法来抑制转子不平衡振动,需反复启、停机,会造成严重的经济损失[1-2]。安装附加阻尼器来抑制转子振动成为转子不平衡振动问题的有效解决方法。磁流变阻尼器作为智能减振阻尼装置,已广泛应用于车辆、土木建筑、大跨结构等方面,取得了良好的减振效果[3]。
Carlson等[4]研究了多种装有磁流变阻尼器的设备,认为磁流变阻尼器由于其良好的性能与简单的使用条件在今后的工业生产中将有广阔的发展前景。Milecki[5]研究了一种半主动控制的磁流变阻尼器,实验结果表明使用磁流变阻尼器可在不减少增益系数的情况下缓解振动问题。祝长生[6]通过实验详细研究了剪切型磁流变脂阻尼器对转子系统动力特性的可控性。王锎等[7]建立了阻尼器-单盘悬臂柔性转子系统,实验研究了单个磁流变阻尼器对转子系统振动的抑制效果。唐少容[8]认为在空间结构中阻尼器的布置数量和方式对抑制由于风荷载引起的振动具有一定的影响。汪建晓等[9]从理论和实验两方面研究了对称安装双磁流变阻尼器在振动控制装置中对振动抑制的影响效果。王修勇等[10]研究了阻尼器在不同安装位置对斜拉桥抑制风雨振现象的影响效果。
上述研究验证了磁流变阻尼器具有良好的抑振效果,并且在空间结构中磁流变阻尼器的数量以及布置方式等均对振动有一定的抑制作用,但并未将多阻尼运用于转子系统中。为了更好地探究磁流变阻尼器对转子振动的抑制规律,本文搭建了双磁流变阻尼器转子实验台,研究在不停机的情况下,阻尼器不同数量及位于不同位置时对转子系统振动的影响规律。
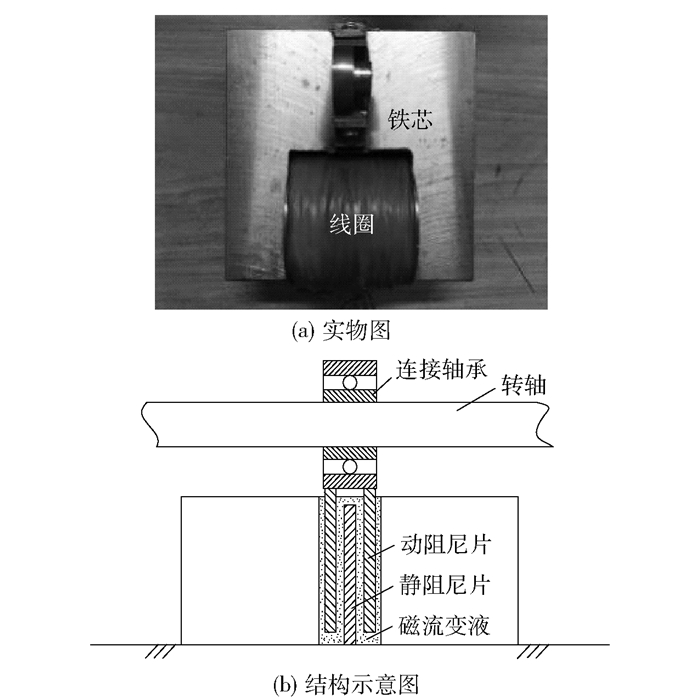
1 磁流变阻尼器的结构与控制原理 1.1 磁流变阻尼器结构本文采用剪切式磁流变阻尼器。动、静阻尼片呈上下交叉排列,其间充满磁流变液,动阻尼片依靠连接轴承与转轴固定在一起,静阻尼片与底板连接。图 1为磁流变阻尼器实物及结构示意图。
|
图 1 磁流变阻尼器实物及结构示意图 Fig.1 Actual view and sketch map of the damper |
实验所用磁流变液是一种有磁性的悬浮液,由羰基铁粉、二甲基硅油按一定比例混合而成,并添加适量活性剂以防止磁流变液颗粒沉降。在无磁场条件下,磁流变液可以自由流动,但是在加入磁场之后,磁流变液从自由流动状态变为半固态,呈高黏度低流动性流体特性,产生随磁场增加而增加的屈服应力。
阻尼力与电流间关系用Bingham模型描述,阻尼力Fm(I, t)为
| $ {F_{\rm{m}}}\left( {I,t} \right) = S\eta u\left( t \right)/h + S{\tau _y}\left( I \right) $ | (1) |
式中:S为磁效面积,η为磁流变液黏度,u为剪切速率,t为时间,I为电流,h为阻尼片间隙,τy为磁流变液屈服应力。
1.2 磁流变阻尼器的控制原理根据转子动力学理论,转子系统在不平衡等外部作用下的运动微分方程为:
| $ \boldsymbol{M\ddot x} + \boldsymbol{C\dot x} + \boldsymbol{Kx} = \boldsymbol{f} $ | (2) |
其中M为质量矩阵,C为阻尼矩阵,K为刚度矩阵,f为转子所受外部激振力矩阵,
在对转子系统进行振动控制时,外加安装的磁流变阻尼器通过个数的增多、与转盘距离的缩小来改变转子系统的阻尼力与刚度大小,从而达到有效降低转子振动的目的。
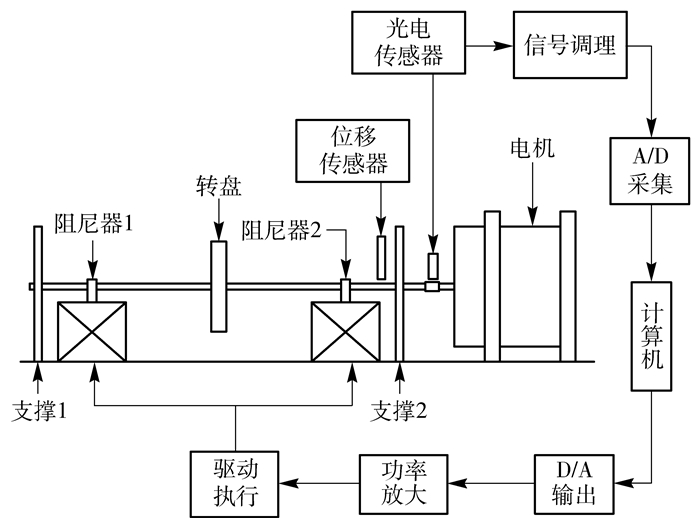
2 实验部分 2.1 实验台参数双阻尼器转子实验台由驱动电机、1个经典Jeffcott转子和2个磁流变阻尼器组成。转子在电机带动下旋转实现无极调速。采用开关控制策略,利用LabVIEW控制程序,实验研究阻尼器不同数量及位于不同位置时对转子振动的抑制效果。实验台实物见图 2,工作原理见图 3,轴系转子基本参数见表 1。

|
图 2 双阻尼器转子实验台 Fig.2 Rotor bench with two-dampers |
|
图 3 转子系统工作原理 Fig.3 Schematic diagram of the rotor system |
| 下载CSV 表 1 转子基本参数 Table 1 The basic parameters of the rotor |
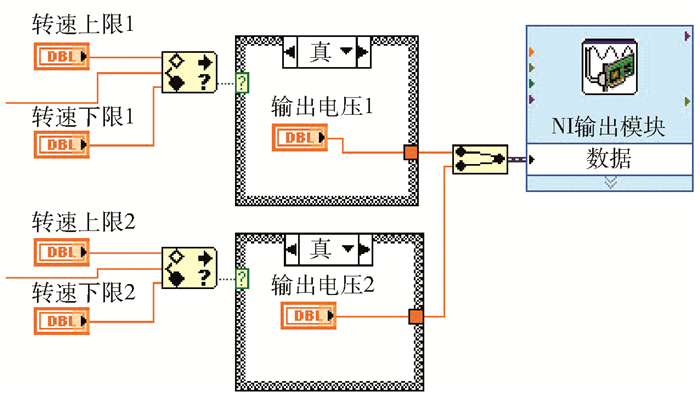
利用LabVIEW软件平台设计一种基于转速的双阻尼器开关控制程序,实验研究在转子运行过程中阻尼器数量对抑制转子振动的影响。控制程序如图 4所示,控制原理如图 5所示。
|
图 4 双阻尼器开关控制程序 Fig.4 On-off control for two dampers |
|
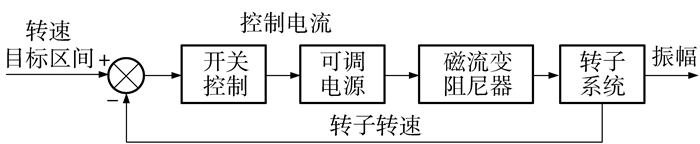
图 5 基于转速的双阻尼器开关控制原理图 Fig.5 Flow diagram of on-off control for two dampers |
基于转速的双阻尼器开关控制通过分别设置两个磁流变阻尼器相应的工作转速区间,实时判断转子转速是否在对应的转速区间内,从而有针对性地控制阻尼器工作,抑制转子振动。
3 结果与讨论 3.1 阻尼器数量对转子振动的影响实验中,磁流变阻尼器1、2分别安装于距转盘中心约150 cm的两侧(见图 2)。实验转子临界转速约1800 r/min,测量转速为0~3000 r/min。
先令磁流变阻尼器1单独工作,设置阻尼器1工作区间为1000~2500 r/min,通入电流为2 A,阻尼器2不通电流。可以发现,当转速超过1000 r/min时,阻尼器1开始工作,转子振幅有明显下降;随着转速的升高,转子振幅明显增大,在临界转速附近振幅达到390.27 μm。
再令双阻尼器同时工作,设置阻尼器1工作区间为1000~2500 r/min不变,阻尼器2工作区间为1500~2500 r/min,两个阻尼器在各自工作区间内均通入2 A电流。
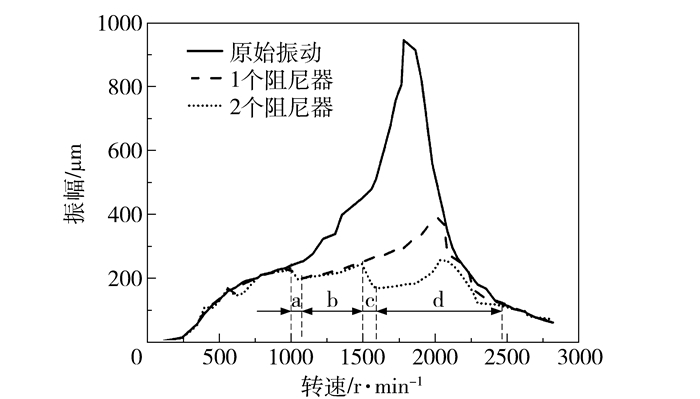
图 6所示为不同阻尼器数量下转子振动幅值曲线。根据程序设定,当转速在1000~1500 r/min时,只有阻尼器1工作,转子振动情况为图(6)中区域a、b;转速达到1500 r/min时,阻尼器2开始工作,如图(6)中区域c所示,转子振动有明显的下降;在1500~2500 r/min区间内,两个阻尼器同时工作,从图(6)区域d可以看到,转子振动幅值随着转速的增加有所上升,在临界转速附近达到最大值250.30 μm,与原始最大振幅相比降幅达72.77%,比单阻尼器降幅高14.07%(表 2)。
|
图 6 不同阻尼器数量下转子系统振幅对比 Fig.6 Variation of vibration amplitude as a fuction of the numbers of dampers |
| 下载CSV 表 2 不同阻尼器数量下转子振动数据 Table 2 Vibration data for a rotor with different numbers of dampers |
改变双阻尼器布置位置,使阻尼器1中心与转盘中心保持150 cm距离不变,阻尼器2分别距离转盘150、130、110、90 cm下,转子实验台实物如图 7所示。实验转子一阶临界转速约1800 r/min,测量转速为0~3000 r/min。设定阻尼器1工作转速区间为1000~2500 r/min,阻尼器2工作转速区间为1500~2500 r/min,在工作区间内,阻尼器均通入2 A电流。

|
图 7 双阻尼器非对称布置转子实验台 Fig.7 Rotor bench with two-dampers in an asymmetric arrangement |
为了更好地体现阻尼器不同位置对转子振动的影响,将转子简化为光轴、圆盘和轴承支撑,利用Dyrobes软件建立转子模型,模拟计算阻尼器2不同位置时的转子振动情况。
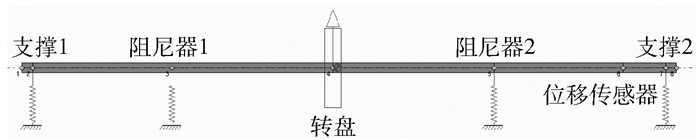
建立转子模型如图 8所示,其中轴承跨距560 cm,节点2和节点7处为轴承支撑位置,阻尼器分别安装在节点3和节点5处。
|
图 8 双阻尼器单跨转子模型 Fig.8 Model of a rotor with two-dampers |
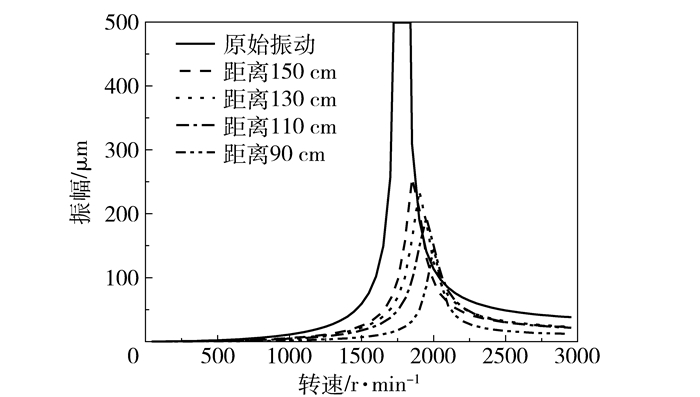
图 9为阻尼器2处于不同位置时,节点6(位移传感器安装位置)的振动情况。可以看到,当双阻尼器均不工作时转子振动达到939.86 μm;当阻尼器1、2距离转盘中心均为150 cm时,转子振幅降至255.44 μm;阻尼器1位置不变,随着阻尼器2与转盘中心距离不断缩小,阻尼器对转子振动抑制效果越来越好,距离130 cm时,振幅为235.74 μm,110 cm时振幅194.03 μm,90 cm时振幅降为147.72 μm。
|
图 9 阻尼器不同位置时转子振动情况(模拟) Fig.9 Comparison of the rotor vibration amplitude with dampers at different positions (simulation) |
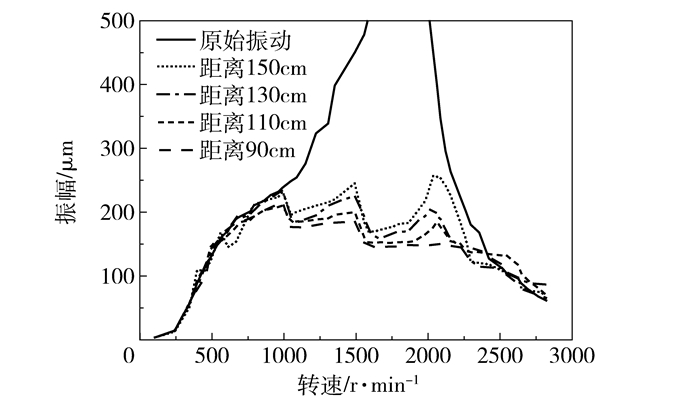
针对阻尼器2位于不同位置时的减振效果进行实验研究,所得数据如表 3所示,振动曲线如图 10所示。从表 3及图 10中可以看出,在相同电流作用下,随着阻尼器2与转盘之间距离不断缩小,振动抑制效果更加明显。保持阻尼器1与转盘中心距离150 cm不变,阻尼器2距转盘150 cm时,利用开关控制双阻尼器同时工作时,临界转速区间内振幅最大为257.30 μm,与原始振动对比,振动降幅为72.77%;改变阻尼器2距转盘130 cm时,振动降幅为77.74%;阻尼器2距转盘110 cm时振动降幅为80.42%;90 cm时振动幅值为150.25 μm,与原始振动相比,降幅达到84.10%。实验与计算结果一致。
| 下载CSV 表 3 阻尼器不同位置转子振动情况 Table 3 Comparison of vibration amplitude data for dampers at different position |
|
图 10 阻尼器不同位置时转子振动情况(实验) Fig.10 Comparison of the rotor vibration amplitude with dampers at different positions (experiment) |
(1) 单个磁流变阻尼器作用下,转子由于不平衡引起的振动有所降低,降幅为58.70%,双阻尼器共同作用下抑制振动效果更显著,降幅达到72.77%。
(2) 磁流变阻尼器距离转盘中心越近,对不平衡引起的振动抑制效果越好。双磁流变阻尼器距离转盘均为150 cm时,振动降幅为72.77%;改变其中一个磁流变阻尼器距离转盘至90 cm时,振动降幅达到84.10%。
(3) 基于转速的双阻尼器开关控制方法可以实现对双阻尼器的单独控制,令两个阻尼器在不同的转速区间内工作,使转子振动始终维持在较小的范围内,可对转子振动进行有针对性的抑制。
| [1] |
孟光. 转子动力学研究的回顾与展望[J]. 振动工程学报, 2002, 15(1): 1-9. Meng G. Review and prospect of rotor dynamics[J]. Journal of Vibration Engineering, 2002, 15(1): 1-9. (in Chinese) |
| [2] |
Rabinow J. The magnetic fluid clutch[J]. Electrical Engineering, 1948, 67(12): 1167. DOI:10.1109/EE.1948.6444497 |
| [3] |
李红云, 柳学全, 滕荣厚, 等. 磁流变液减振器[J]. 金属功能材料, 2005, 12(2): 38-41. Li H Y, Liu X Q, Teng R H, et al. Magnetorheological fluid shock absorber[J]. Metallic Functional Materials, 2005, 12(2): 38-41. (in Chinese) |
| [4] |
Carlson J D, Catanzarite D M, Clair K A. Commercial magneto-rheological fluid devices[J]. International Journal of Modern Physics B, 1996, 10(23/24): 2857-2865. |
| [5] |
Milecki A. Investigation and control of magneto-rheological fluid dampers[J]. International Journal of Machine Tools & Manufacture, 2001, 41(3): 379-391. |
| [6] |
祝长生. 剪切型磁流变脂阻尼器转子系统的动力特性[J]. 机械工程学报, 2006, 42(10): 91-94. Zhu C S. Dynamic behavior of shear-type magnetorheologic grease damper rotor system[J]. Chinese Journal of Mechanical Engineering, 2006, 42(10): 91-94. (in Chinese) DOI:10.3321/j.issn:0577-6686.2006.10.015 |
| [7] |
王锎, 何立东, 邢健, 等. 磁流变阻尼器控制双跨转子轴系振动研究[J]. 振动与冲击, 2015, 34(2): 150-153. Wang K, He L D, Xing J, et al. Two-span rotors system's vibration control by magneto-rheological dampers[J]. Journal of Vibration and Shock, 2015, 34(2): 150-153. (in Chinese) |
| [8] |
唐少容. 布置方式对MR阻尼器在网壳结构风振抑制中的影响及规律[J]. 工程建设与设计, 2007(12): 18-20. Tang S R. Study of impact of distribution on the wind-induced vibration reduction of spatial reticulated shell structures with MR dampers introduced[J]. Construction & Design for Project, 2007(12): 18-20. (in Chinese) DOI:10.3969/j.issn.1007-9467.2007.12.006 |
| [9] |
汪建晓, 孟光. 磁流变液阻尼器用于振动控制的理论及实验研究[J]. 振动与冲击, 2001, 20(2): 39-46. Wang J X, Meng G. Theoretical and experimental study on the vibration control by magntorheological fluid dampers[J]. Journal of Vibration and Shock, 2001, 20(2): 39-46. (in Chinese) |
| [10] |
王修勇, 陈政清, 高赞明, 等. 磁流变阻尼器对斜拉索振动控制研究[J]. 工程力学, 2002, 19(6): 22-28/48. Wang X Y, Chen Z Q, Gao Z M, et al. Study of mitigating vibration on stay cables using magneto-rheological damper[J]. Engineering Mechanics, 2002, 19(6): 22-28/48. (in Chinese) |








