With the rapidly developing electronic technology, hospitals are adopting an increasing number of electronic equipment, including the picture archiving and communication systems (PACS) [1]. In such systems, the diagnosis results of patients are stored in the form of digital images. These images contain the patients' personal information. Random access to these images may cause serious social problems [2]. Consequently, storing and safely transferring patient data are presently becoming hot topics.

Using cryptography technology to protect digital information is an effective method. In the 1970s, conventional encryption algorithms, such as data encryption standard (DES), advanced encryption standard (AES) and international data encryption algorithm (IDEA) [3] processed information as a binary stream. A digital image has its own characteristics, such as high correlation in adjacent pixels, data redundancy, uneven distribution of energy, etc. [4]. Hence, the conventional encryption algorithm cannot be successfully applied to a digital image.

In recent years, increasing attention has been focused on the research of an image encryption technique based on chaos synchronization [5]. Many methods were adopted to realize chaos control and synchronization. These included the control Lyapunov function [6], nonlinear control [7], adaptive control [8], back stepping control [9], passive control [10], and sliding-mode control [11] methods, etc. In a real physical process, some time-delays are trivial, such that they can be ignored. However, others cannot be disregarded, particularly in long-distance communication and with transmission congestion. Therefore, studying the synchronization in such systems with delays is important and necessary [12–15].

In this study, we mainly focused on the medical image encryption technology based on chaos synchronization. Firstly, we deal with the problem of designing a linear controller to realize the chaotic synchronization for the time-delay chaotic system. Subsequently, we apply the newly developed method in the research of medical image encryption. Thirdly, some simulation works are presented to illustrate the feasibility of the proposed algorithm.

Some necessary lemmas are introduced herein before the main results are presented.

Suppose C=C([-r, 0], Rⁿ) is the Banach space of continuous functions mapping the interval [-r, 0] into Rⁿ with the topology of uniform convergence. Let x_t ∈ C be defined by x_t(θ) = x(t+θ), -r≤θ ≤ 0.

The following autonomous equation must be considered as

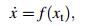
(1)

where f : C→Rⁿ is a completely continuous function, and the solutions of Eq. (1) continuously depend on the initial data.

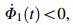
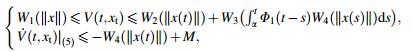
Lemma 1 [16] Let V(t, x_t) be a differentiable scalar functional for all t ≥ 0 and x_t ∈ C. M is a positive number. If there is a bounded continuous function Φ₁[0, ∞) → [0, ∞), which is L¹[0, ∞) with Φ₁(t) → 0 as t → ∞, such that

(2)

where W_i (i = 1, 2, 3, 4) is a wedge, and the solutions of Eq. (1) are uniformly bounded.

Lemma 2 [17] We are particularly interested in the globally asymptotically stable (GAS) problem of the cascade delay system in the following form

(3)

where . We assume that f₁ and f₂ are completely continuous. They satisfy enough additional smoothness conditions to ensure the solutions of Eq. (3) continuously depending on the initial data. We also assume that f₁(0) = 0 and f₂(0, 0) = 0.

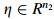
If

(ⅰ) the equilibrium η = 0 of system 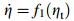is GAS;

(ⅱ) the equilibrium Ψ = 0 of 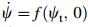is GAS; and

(ⅲ) the solution of the whole system (Eq. (3)) is bounded.

The equilibrium Ψ=0, η=0 of the whole system (Eq. (3)) is GAS.

Lemma 3 [18] Let a₁ and b₁ be the two n-dimensional vectors, and 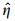be an arbitrary positive real number. The following inequality then holds

(4)

This study aims to design a linear controller for the chaotic secure communication system with state delay to realize the synchronization between the transmission and the reception ends. Therefore, the original message can be recovered at the reception end.

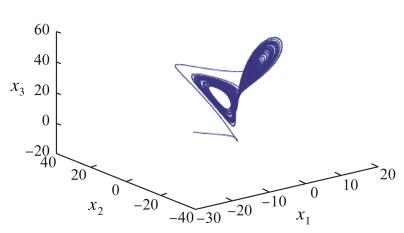
Consider the following time-delay chaotic system as the transmitter system

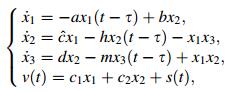
(5)

where x₁, x₂, and x₃ are state variables; a, b, 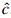, d, h and m are the system parameters; τ is the time lag; s(t) is the signal to be transmitted; and v(t) is the transmitter system output. The system (Eq. (5)) may be in the chaotic state through a suitable selection of the system parameters and time delay. The system (Eq. (5)) is in the chaotic state (see Fig. 1) when m = 10, and s = 0.

Fig. 1 Chaotic attractor of the time-delay system (Eq. (5))

Figure options

The receiver system is presented as

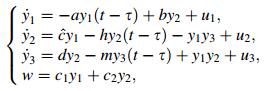
(6)

where w is the output of the receiver system, and u₁, u₂ and u₃ are the controllers to be designed. We assume here that all the states y₁, y₂ and y₃ are available for the feedback controller. The synchronization errors are denoted as e_i = y_i -x_i(i = 1, 2, 3). Subtracting Eq. (6) from Eq. (4) yields the following error system

(7)

The slave system (Eq. (6)) can successfully synchronize the drive system (Eq. (5)) if the synchronization error system (Eq. (7)) is stable. We will adopt three steps in the following to design the linear controllers that attain this goal.

Step 1 Design u₁ = -be₂ -k₁e₁, where the controller parameter k₁ can be determined later by the solution of a linear matrix inequality (LMI). The first equation of the error system (Eq. (7)) will be presented as follows when the controller is applied

(8)

In the following, we will prove that the error system (Eq. (8)) is asymptotically stable and bounded. The following candidate of the Lyapunov-Krasovskii function is considered as

(9)

Its derivation along the solution of the system (Eq. (8)) is then calculated, and we obtain

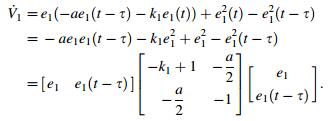
(10)

We know from the Lyapunov-Krasovskii stability theory that the error system (Eq. (8)) will be asymptotically stable and bounded if a scalar k₁ exists, such that the following LMI is solvable

(11)

In other words, a constant ρ₁ exists, such as |e₁| ≤ ρ₁.

Step 2 Consider the second and third equations of the error system (Eq. (7))

(12)

The system (Eq. (12)) can be simplified as follows when e₁ = 0

(13)

The linear controllers should then be designed as u₂ = -k₂e₂(t), u₃ = -k₃e₃(t), where the controller gains k₂, k₃ are to be later determined by the solution of an LMI.

Consider the following candidate of the LyapunovKrasovskii function

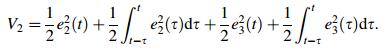
(14)

Its derivation along the solution of the error system (Eq. (13)) is calculated to obtain

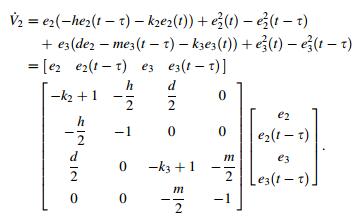
(15)

We know from the Lyapunov-Krasovskii stability theory that the simplified error system (Eq. (13)) is asymptotically stable if two real numbers (i.e., k₂ and k₃) exist, such that the following LMI is solvable

(16)

We can see that the error system (Eq. (13)) is greatly simplified than Eq. (12) because we can consider e₁ as zero. Any item coupled with e₁ can be treated as zero, which is one advantage of the proposed method.

Step 3 In this step, we will prove that the solution of the whole error system (Eq. (7)) is bounded. Step 1 showed that the error state e₁ was bounded by a positive constant ρ₁. Hence, we only need to prove that the error states e₂ and e₃ are bounded under the suppression of the linear controller u₂, u₃. Consider the following candidate positive function

(17)

Its derivation along the error system (Eq. (7)) is calculated to obtain

(18)

We know from Step 1 that |e₁| is bounded by |e₁| ≤ ρ₁. The transmitter system (Eq. (6)) is a chaotic system; hence its states are bounded. Some positive constants, such |x_i| ≤ k_i, are then found to exist. We can obtain the following equation from Lemma 3

(19)

where η_i(i = 1, 2, 3) are arbitrary positive constants.

Subsequently, we can obtain the following inequality

(20)

Denote

(21)

We can see that M is a positive constant. We can conclude from Lemma 1 that the solutions of the error system (Eq. (7)) will be bounded if some positive real numbers η_i(i = 1, 2, 3) and general real numbers k_i(i = 2, 3), such that the LMI Φ < 0, exist. Combining the proof process of Steps 1-3, we know from Lemma 2 that the time-delay chaotic error system (Eq. (7)) can be stabilized by the linear controller u_i(i = 1, 2, 3).

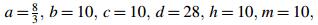
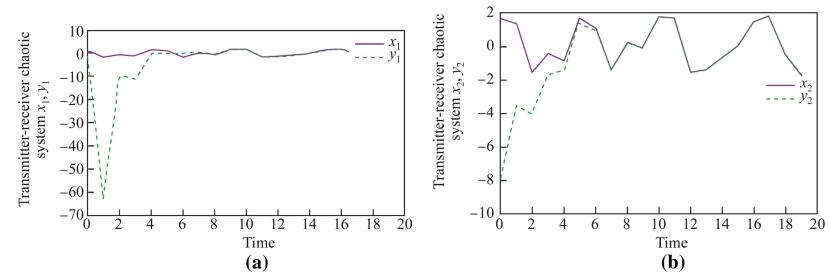
The simulation work herein was processed in MATLAB R2010a. A DDE23 solver was used to solve the delay differential equations. The parameter values are as follows: and s = 0: The simulation results of the transmitter-receiver chaotic system synchronization could be seen in Figs. 2 and 3.

Fig. 2 State trajectories of the transmitter-receiver chaotic systems xi, yi(i = 1, 2)

Figure options

Figure 2 shows that the trajectories of the receiver systems can asymptotically approach the trajectory of the transmitter chaotic systems, while Fig. 3 illustrates that the error states asymptotically approach zero. The controller proposed was linear and easy to be applied in a real physical process.

Fig. 3 States response of the error system

Figure options

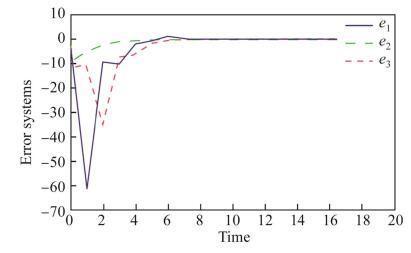
In the process of secure communication, the signal "s" to be transmitted is first embedded in the chaotic signals. The synthesized signal will then be transmitted through a common channel. A slave chaotic system is used at the receiver terminal. The controller in the receiver terminal can drive the system to synchronize with the transmitter system, and the original signal "s" can be decrypted. Figure 4 shows a diagram of the whole process.

Fig. 4 Overall framework

Figure options

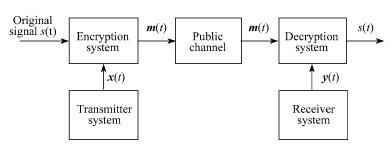
In this section, a medical skull image P measuring M × N was used for encryption. x₁(0), x₂(0) and x₃(0) were the initial values of the transmitter system. Although the transmitter (Eq. (5)) and receiver (Eq. (6)) systems were continuous systems, the simulation work was conducted using a computer, and discrete sequences were produced. Hence, we can directly utilize the sequence produced by MATLAB to do the encryption work. An encryption method was proposed in Ref. [19], shown as follows.

Step 1 Transform the plain matrix P₀ to a vector 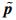of length M × N.

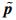
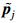
Step 2 Divide the obtained vector into S blocks of length N_k. N_k is a variable value given by the following function.

(22)

where N₁ is determined by the user and .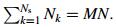

Step 3 Generate a chaotic sequence (x_j^k), j = 1, 2, ..., N_k, k = 1, 2 of length N_k. The sequence is generated by iterating the chaos system given by Eq. (5).

Step 4 Quantize the (x_j^k), j = 1, 2, ..., N_k coefficients by applying Eq. (23). Here, denote the obtained key stream as

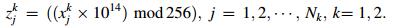
(23)

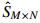
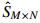
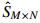
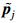
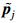
Step 5 Sort the chaotic sequences according to the ascending order to get the address sequence code and R_M×N. According to the address sequence code , sort the blocks of length N_k. In the same way, we sort the according to the address sequence code R_M×N.

After verification, we found that the method of Ref. [19] was effective for the general image. The medical image mainly contained the black and white colors. Hence, dividing it into different blocks was hard. This method was not suitable for the medical image, and realizing the encryption took much time. Figure 5 shows the encryption result.

Fig. 5 Result of verification

Figure options

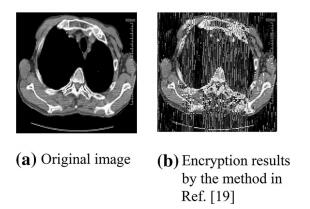
We aim to improve and optimize this method in combination with the inherent characteristics of a medical image.

Step 6 Generate the cipher blocks (c_j), j = 1, 2, ..., N_k by applying

(24)

Step 7 Concatenate. Firstly, let's construct a vector c of length MN from the blocks (c_j), j = 1, 2, ..., N_k. Also, we can denote this vector as c(MN). Then two chaotic sequences (x_j^k), j = 1, 2, ..., N_k; k= 1, 2 of length M × N can be generated by iterating the chaotic system (Eq. (5)).

Step 8 Embed the signal s in the output of the drive system by v = c₁x₁ + c₂x₂ + s. Here, v is a vecotor containing M × N elements and we can denote it as v(MN). Then the original image can be encrypted by reshaping the vector v to a matrix V₀ of size M × N.

The whole encryption process can be described in Fig. 6.

Fig. 6 Encryption flow chart

Figure options

The image was encrypted after the abovementioned steps have been performed. The image signal can by recovered if the receiver system synchronizes the transmitter system. The decryption process is the inverse process of the encryption process, and it is omitted here.

A medical skull image measuring 128 × 128 was adopted in this section as the signal to be encrypted (see Fig. 7). The encryption key was generated by the transmitter chaotic system. Figure 8 shows the obtained encryption image.

Fig. 7 Original medical skull image

Figure options

Fig. 8 Encrypted skull

Figure options

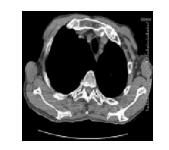
The slave chaotic system (Eq. (6)) was used to generate the decryption key. The decrypted image can be obtained after the above decryption process (see Fig. 9).

Fig. 9 Decrypted skull

Figure options

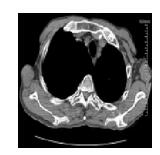
The peak value signal-to-noise ratio (PSNR) is usually used to evaluate the visual impression of the cipher image. The cipher image was equal to add noise to the plain image. The encryption effect defined as follows will then be better when the PSNR value (RPSN) is lower:

(25)

where Ψ_max is the maximum of the pixel color component; p_ij and c_ij represent the value of the pixel (i, j) in the plain and cipher images, respectively. R_PSN < 20 dB means that the cipher image is impossible to identify. Table 1 shows that the PSNR values of the encrypted color components are all less than 9.4 dB and indicates that the information is effectively covered.

Table 1 Value of PSNR in the encrypted image

Table options

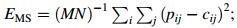
The standard test medical image of size 128 × 128 was selected herein to test the property of the resisting statistical analysis. We randomly selected 1 000 pairs of two adjacent pixels, including vertically, horizontally, and diagonally adjacent pixels, to calculate the correlation of the two adjacent pixels. We then calculated the correlation coefficient of each pair using the two following formulas [20]

(26)

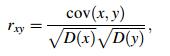
(27)

where x and y are the gray-scale values of the two adjacent pixels in the image. The following discrete formulas are employed in the numerical computation

(28)

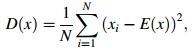
(29)

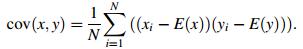
(30)

Table 2 shows the results of the horizontal, vertical, and diagonal directions. The correlation coefficients of the cipher images were very small, which implied that no detectable correlation existed between the original and its corresponding cipher images. Therefore, the proposed algorithm had high security against statistical attacks.

Table 2 Correlation coefficient of adjacent pixels

Table options

This paper proposed a novel linear feedback controller to achieve synchronization and secure communication in time-delay chaotic systems. A secure message can be successfully recovered. The key has a long enough period and can be used for medical image encryption. Compared with the general image, the medical image has large pieces of black and white areas. This characteristic enables the traditional encryption to have no obvious effect. The proposed algorithm made up for the shortcomings, and the numerical simulations were provided to show the effectiveness of our methods.