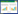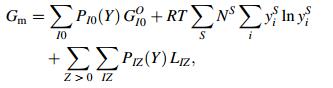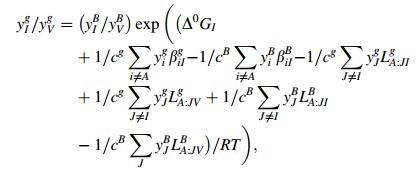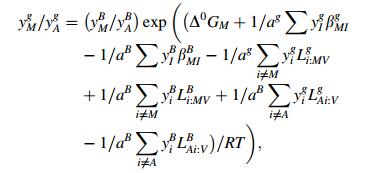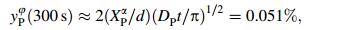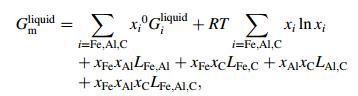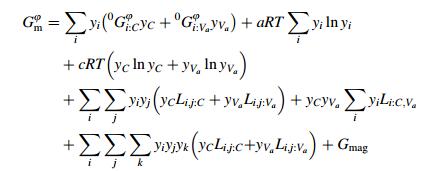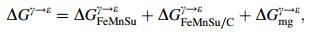The article information
- Li Lin, Jiang Hu
- Application of thermodynamics in designing of advanced automotive steels
- Advances in Manufacturing, 2016, 4(4): 340-347.
- http://dx.doi.org/10.1007/s40436-016-0156-3
-
Article history
- Received: 25 July, 2016
- Accepted: 28 September, 2016
- Published online: 23 November, 2016
During the latest 30 years, there was a surge for coupling thermodynamics and phase diagram in the field of materials science and engineering. Many effective programmers as well as the exploring of versatile solution models, e.g., the wildly used compound energy model were developed. Thermo-calc, as one of the most successful commercial software packages for calculation of phase equilibrium from a broad database, offered appropriate guidance for the materials study and reduced largely the amount of experiments.
However, there was still far from much work in the field of prediction or estimation based on the principles of thermodynamics and kinetics for the practical processes in mass production or designing for kinds of materials. This paper aims at introducing some computational results on the designing of advanced materials. As understanding of essence of materials is a matter by degrees and technology in manufacturing is quickly developing, design of material and its processing can be phased step by step. In order to limit the paper length, only little examples were shown and all of them were stressed at advanced automotive steels.
2 Designing transformation induced plasticity (TRIP) steel 2.1 Newtype TRIP steel containing AlIn 1990’s, low alloy TRIP steel with a simple composition 0.45%C-1.5%Mn-1.5Si% [1] received significant interest in industrial and scientific community since it exhibited, for deep drawing application in automobile factories, excellent combination of both high strength and formability, which came from transformation induced plasticity of retained austenite. The amount and stability of retained austenite were the key factors to influence transformation behavior during straining.
High Si content in the steel suppressed the formation of cementite and led to an increase of the stability and amount of retained austenite. However, high Si content would also cause troubles in steel production, such as strong oxide layer, poor surface characteristics, low coat-ability and thus galvanizing problems.
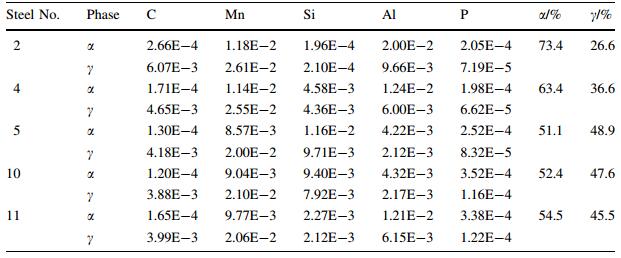
Efforts were made to improve the composition concept. In the first phase, different amount of Al was added as an alternative to the steel to substitute for Si, as shown in Fig. 1 [2]. The overall compositions of five different steels were listed in Table 1 [2], where steels No. 2, 4, 11 with high Al content were designed as the galvanizing favorite material with high requirement on elongation, and steels No. 5 and 10 were compared materials.

|
| Fig. 1 Mechanical properties of the various TRIP aided steels after different heat treatments [2] |
Simulation of the inter-critical annealing at 780 ℃ of steels was performed with thermo-calc and its database. The Gibbs free energy of an arbitrary phase was listed as
where the first summation in Eq. (1) represents the standard energy, the second the mixing entropy and the third the excess Gibbs energy. The results [2] (see Table 2) shows that steels No. 2 and 4 have good plasticity and fairly good strength since both have high volume fraction of α phase (ferrite), though the γ phase (austenite) is less. It still can induce some bainite transformation in the low temperature and raise the strength of the steels.
|
Mechanical properties of steels No. 2 and 4 were in accordance with thermodynamic estimation. Steel No. 11 exhibited a bit higher strength but relatively low elongation since it had higher amount ofγbut lower α phase. Different from steels No. 5 and 10, steels No. 2, 4 and 11 therefore exhibited both super coat-ability and satisfactory mechanical properties due to their high Al content. These three steels mentioned above were adopted and produced in ThyssenKrupp stahl and Voest-Alpine Arcelor, and the sheet steels were manufactured as important structural parts, e.g., reinforcement A-pillars and B-pillars in FIAT and PORSCHE, which were the pioneer companies in the organization of ultra-light steel auto body (ULSAB).
2.2 TRIP steel containing PAs stated above, the substitution of Si by Al was successful [2] but soon after the production of the new TRIP steel. It was found when Al content was higher than 0.5%, clogging during continuous casting at the time might occur due to the precipitation of aluminum oxide. Searching for other effective element to substitute Si was then triggered [3]. In the periodic table of element, Al, Si, and P were located closely in the same period, and these elements would have similar electronic structures as well as similar properties. It was then natural to consider P as another substitute for Si. P could, on one hand, prevent cementite precipitation and increase the stability of austenite. On the other hand, it had a strong tendency to segregate at grain boundary and induce cold brittleness. Segregation formulation was developed by Guttmann and Mclean in a ternary system (Fe, M, I) [4] based on the sublattice model in melt salts and stoichiometric phases contributed by Hillert et al. [5]. Li et al. [6, 7] extended the segregation equation, and generalized it into a multicomponent system as
where y represents the site fraction in sublattice, g grain boundary, B base, V vacancy, A base metal, J and I impurity, i and M metal element, cand a fraction of sites available both in grain boundary or matrix, Δ0GI and Δ0GM the intrinsic segregation Gibbs free energy of impurity I and metal element M. LA:JIB(g) denoted the interaction energy between J and I in one sublattice when another sublattice was fully occupied by element A. βMIB(g) meant the interaction energy between elements in different sublattices. According to Refs. [7, 8], assuming that interaction energy keeps the same as on grain boundaries and in matrix and omitting the interaction between impurities and vacancy and between metal element and iron, a series of parameters [7, 8] can be listed as follows: ag=cg=0:5, aB=0:75, cB=0:25, Δ0GP=47 kJ/mol, Δ0GMn=8 kJ/mol, βMnP=12.5 kJ/mol, LFe:PC=-9 kJ/mol. With all the data stated above and an assumed steel composition with enough high content of phosphorus (C=0.15%, Mn=1.6%, Si=0.3%, P=0.07%), the equilibrium segregation amount of phosphorus on grain boundaries at 400 ℃ was calculated as 32% [9], which was high enough to cause temper brittleness. In calculation, the soaking temperature 400 ℃ at the over-aging process was set according to the practical process parameter. However, the actual soaking was quite quick, normally for 3-5 min, being far from equilibrium condition. Thus, the estimated equilibrium segregation amount of phosphorus was not suitable to describe the over-aging process of TRIP steels.
Based on Mclean’s kinetic approach for a binary system [10], the amount of segregative element on grain boundaries was expressed as
where yiφ (t) is the grain boundary coverage of element i at time t, yiφ (0) its initial value and yiφ the equilibrium value. Di denotes bulk diffusion coefficient of i, d the grain boundary thickness and Xiα mole fraction of i in base. Taking d=10-7 cm as usual, t=5 min=300 s and T=673 K according to the actual process condition, XPα=1.387 9 10-3 (i.e., mass fraction=0.07%), yiφ (0)=0. According to Sundman et al. [11], DP=3.53 9 10-18. Thus, the segregated amount of P at grain boundary after soaking at 400 ℃ for 300 s was [9]
which was small and would not be of any damage in grain boundary for the TRIP steel. Moreover, cold fracture test was applied with the structural part assembles of automobiles and no sign of cold brittleness was detected. The new type TRIP steel containing P was manufactured according to the design stated above in Ansteel company group in China.
2.3 Attractive effect of Al in TRIP steelExploring thermodynamic property of aluminum and its function in steel manufacturing is a time consuming work. Recently it was found in the first place [12] that with the existed database the phase diagram of the steel containing a certain amount of Al could not be described accurately and it should be revised. They used high purity Fe (99.99% mass fraction, Source), Al (99.97% mass fraction, Source) and C (99.99% mass fraction, Source) to prepare different composition Fe-Al-C alloys, as shown in Table 3.Dilatometer experiments were carried out in a formaster-D dilatometer to detect the ferrite to austenite transformation temperatures during the heating and cooling cycles. The results were listed in Table 3.
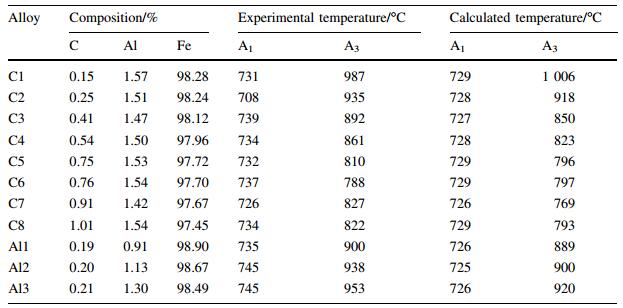
|
With the new set of experimental data, the Fe-Al-C system in Fe-rich corner was optimized. The molar Gibbs energy of the ternary liquid phase was described by the Redlich-Kister polynomial [13]
where xi was the mole fraction of element i and 0Giliquid was the Gibbs energy of liquid Fe, Al and C. The binary parameters Li, j were obtained from the thermodynamic evaluation of the limiting binaries, whereas the LFe, Al, C was a ternary interaction parameter.
Gibbs energy of solid phases, fcc (austenite), bcc (ferrite) and hcp in the Fe-Al-C system was described by a compound energy formalism consisting of substitutional and interstitial sublattices [14]. The crystal structure was therefore modeled as (Fe, Al)a (C, Va)c.
Symbols a and c denoted the numbers of sites which were dependent on the crystal structure. Here the values of a and c were regarded as a=1, c=1, 3, and 0.5 for the fcc, bcc and hcp phases respectively. The molar Gibbs energy was expressed as follows
where i, j=Fe, Al and K=C or Va. In Eq. (7), yi was the site fraction of component i in its sublattice. 0Gi:Va was the Gibbs energy of pure element i in a relevant nonmagnetic state and 0Gi:C was the Gibbs energy of a hypothetical non-magnetic state, where all interstitial sites were occupied by carbon. All G values were given relative to the reference state. Gmag was the magnetic part of the Gibbs energy.
In the Fe-Al-C system, only one ternary K phase was reported besides the liquid, fcc, bcc and hcp phases. In this optimization, the description of the K phase was after the thermodynamic assessment of Kumar et al. [15]. Li et al. [12] optimized the Fe-Al-C ternary system based on the previous thermodynamic description of the Fe-C, FeAl and Al-C systems [15, 16] as well as the obtained dilatometer data [12]. Furthermore, Li et al. [12] extrapolated the thermodynamic properties of the limiting binary and ternary systems to higher order systems to construct the self-made database, especially for TRIP steels containing elements as Mn, Si, Al, C, Nb and V. A calculated vertical section of the Fe-Mn-Si-Al-C system was shown in Fig. 2 meeting very well with the experimental results.
|
| Fig. 2 Extrapolated vertical section of the Fe-Mn-Si-Al-C steel with 1.60% Mn, 0.37% Si, and 1.31% Al (mass fraction) [12] |
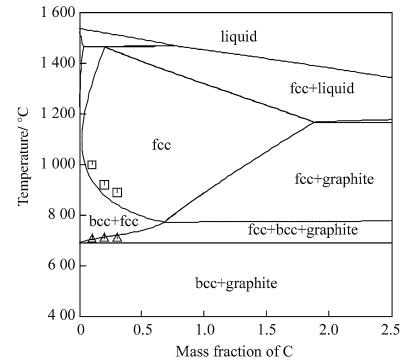
For exploring the difference in phase diagrams of steels with and without Al, the diagrams of Fe-1.5Mn-0.2C steel and Fe-1.5Mn-1.2Al-0.2C were calculated with the selfmade database, as shown in Fig. 3. As calculated, when at 780 ℃, the carbon content in fcc phase in Fe-Mn-Al-C steel was 0.76%, while in Fe-Mn-C steel was only 0.29%. That meant if soaking at the same temperature, the former dissolved more than two times carbon in the fcc phase resulting much higher stability of fcc phase and much better TRIP effect. This new finding brings substantial improvement for the mechanical properties for steels since Al can largely increase carbon solubility in fcc phase. Following this idea, i.e., keeping reasonably high amount Al in the steel and treating it in an ordinary TRIP process, a high performance steel can be obtained whose strength and ductility product reaches 30 000 MPa. It is actually the property target of a third generation steel [17]. The new understanding of Al function in phase diagram and thermodynamic properties must lead to substantial progress in steel application due to the fact that refining of steel with rather high solubility of Al is not a problem in modern steel plant at all.

|
| Fig. 3 Phase diagram of the Fe-Mn-Al-C and Fe-Mn-C steels calculated by self-made database |
Recently twin induced plasticity (TWIP) steel was developed showing the highest elongation rate (≥80%) and fairly good strength (600 MPa) due to the effect of TWIP. But in practical use, e.g., automobile anti-crash parts, the strength seems to be low but ductility too high. With further consideration of alloy concept, much high strength may be obtained for the steel that comes from hcp (ε) martensite transformation. As known, hcp martensite phase transformation is related to the stacking-fault energy (SFE) in austenite, which is affected by the special characteristics of alloy elements and their interactions and is discussed in Ref.[18].
For pure metal, stacking-fault energy can be considered as Gibbs free energy difference between γ atoms with two layers of fcc and ε atoms with two layers of hcp. While for alloy, the Gibbs free energy difference between fcc and hcp is not strictly equal to stacking-fault energy, because the element concentration at stacking faults is different from the average composition of alloy, especially the Suzuki effect caused by C, N, which leads to the obvious difference of concentrations between stacking faults and base material. According to the pioneer work of Olson and Cohen [19], the thermodynamic model of stacking-fault energy was expressed as
where 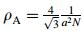
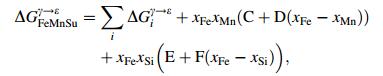 (10)
(10) where ΔGiγ→ε is the transformation free energy difference of γ→ε in pure components i. xi the mole fraction of element i, T temperature in Kelvin, the last two items in Eq. (10) represented the interaction between Fe-Mn and Fe-Si, where the interaction between Fe and other elements as well as the mutual action of alloy elements were neglected. The parameters of C, D, E, F in Eq. (10) were obtained form the corresponding curve fitting and listed in Table 4 after Dumaya et al. [21]. ΔGFeMnSu/Cγ→ε in Eq. (9) represented effect of interaction between all the substitute elements, and carbon on the transformation free energy as
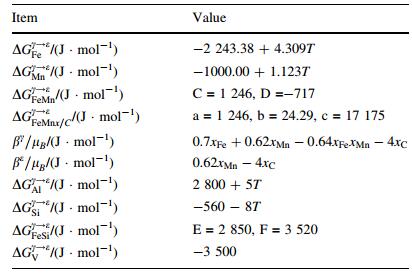
|
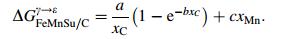 (11)
(11) While ΔGmgγ→ε was the mole magnetic free energy difference between γ phase and ε phase
where Gmε, Gmγ denoted respectively the mole magnetic free energy of γ phase and ε phase [22-24].
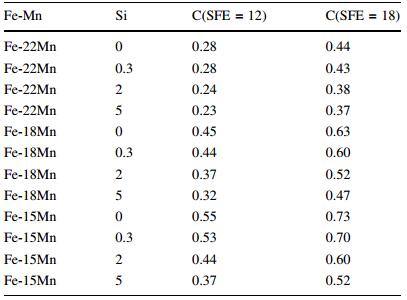
Allain et al. [20] considered for Fe-Mn-C system, if stacking-fault energy (SFE) was higher than 12 mJ/m2, austenite was easy to induce twins; if the SFE lower than 18 mJ/m2, this phase was easy to induce hcp martensite. The suggestion of Allain et al. [20] was that the SFE value in 12-18 mJ/m2 was adopted as the value which induced martensite transformation in the TWIP steel by Li et al. [18]. The calculation result for a steel with 18%Mn but different Si and C was shown in Fig. 4, where the composition range suitable for the assigned SFE was indicated.

|
| Fig. 4 Estimated SFE in Fe-18Mn-YSi-C alloys [20] |
Steels with different Mn, Si and C content but their SFE ranged in 12-18 mJ/m2 was calculated and listed in Table 5 [18].
For designing the test steel, a value of stacking fault energy in the range of 12-18 mJ/m2 was adopted. The change of carbon content was used to adjust the size of stacking fault energy while the content of Mn was to be set as low as possible to be favorable to metallurgy process. Based on the above calculation the composition of the high strength high ductility steel was designed as 16%-22%Mn, 0.3%-0.6%C and 0.2%-0.8%Si.
In order to raise the mechanical property of the steel, different heat treatments after hot rolling was applied. Table 6 shows different final rolling temperatures and cooling methods after hot rolling.
Figure 5 showed the XRD spectra of the test steels treated with different heat treatments after hot rolling. It could be seen that the microstructure was the combination of austenite and ε-martensite after hot rolling at 850 ℃ and water quenching, but was austenite alone after other treatments. Figure 6 shows the strain-stress curves of the test steels treated with different methods. It was seen that air cooling after hot rolling (as Mn18_3 steel) led to the best property of steel whose strength was higher than 1GPa and elongation rate above 60%. To examine the effect of structure on property, the fracture sections of steels were analyzed with XRD as shown in Fig. 7. It would be found that ε-martensite peak appeared in the fracture of three specimens. Among this peaks, ε-martensite peak in Mn18_3 specimen was the weakest. Therefore, from the XRD results before and after drawing and the result of tensile test, it was followed that ε-martensite existed before tensile test as well as a great amount of ε-martensite induced during tensile test both raised the strength of the steel, while only a bit of induced ε-martensite during tension improved the property much effectively. All those steels exhibited strength higher than 800 MPa caused by martensite transformation.
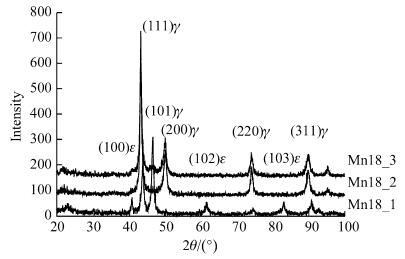
|
| Fig. 5 XRD spectra of hot rolling steel [18] |
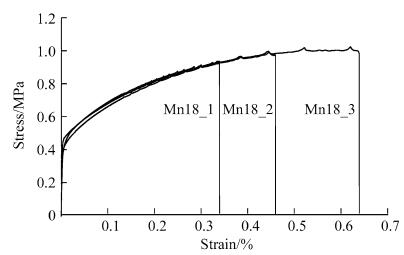
|
| Fig. 6 Stress-strain curves of hot rolling steels [18] |
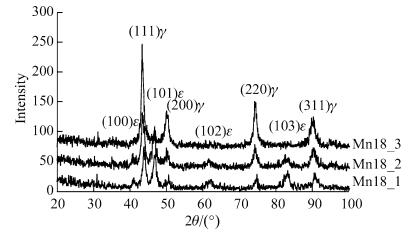
|
| Fig. 7 XRD spectra of hot rolling steel after deformation [18] |
Combining with the calculation results and experimental process stated above, new type of high strength and ductility TWIP steel was successfully produced in Ansteel group.
4 ConclusionsAn aspiration of engineers in materials field is to have the possibility to estimate in advance the composition, properties, processing parameters, etc., while they are planning to develop a new material. This paper offers a basic sketch where one could find how thermodynamics, coupled with accurate experiment results, constructs the entrance for mass production. Examples are briefly introduced which include developing new type steel, improving the quality of existed steel and discussing the factors mainly influencing steel property.
Acknowledgement This work is financially supported by the National Key Basic Research Development Project of China (Grant No. 2010CB630802), the National Natural Science Foundation of China (Grant Nos.50934011 and 50971137) and Shanghai University.| 1. | Matsumumura O, Sakuma Y, Takechi A(1987) Enhancement of elongation by retained austenite in intercritical annealed 0.4 C-1.5 Si-0.8 Mn steel. Trans. ISIJ, 27, 570 doi:10.2355/isijinternational1966.27.570 |
| 2. | Li Lin, De Cooman BC, Wollants P, et al(2004) Effect of aluminum and silicon on transformation induced plasticity of the TRIP steel. J Mater Sci Technol, 20(2), 135-138 |
| 3. | Li L, Liu R, Shi W et al (2009) Development of a new type TRIP steel with good weldability and galvanizing property. In:Proceedings of international symposium automobile steel, Dalian, China, 2009, pp 332-336 |
| 4. | Guttmann M, Mclean D (1979) Grain boundary segregation in multicomponent systems. In:Johnson WC, Blakely JM (eds) Interfacial segregation. ASM, Metals Park, pp 261-348 |
| 5. | Hillert M, Staffansson LI(1970) Regular-solution model for stoichiometric phases and ionic melts. Acta Chem Scand, 24, 3618 doi:10.3891/acta.chem.scand.24-3618 |
| 6. | Li L, Delaey L, Wollants P, et al(1993) Thermodynamic analysis of the segregation of multicomponent steels. J Chim Phys, 90, 305-311 |
| 7. | Li L, Delaey L, Wollants P, et al(1996) Thermodynamic calculation of segregation in multicomponent steels. J Mater Sci Technol, 12(3), 238-240 |
| 8. | Guttmann M, Dumoulin Ph, Wayman M(1982) The thermodynamics of interactive co-segregation of phosphorus and alloying elements in iron and temper-brittle steels. Metall Trans, 13A, 1693-1711 |
| 9. | Li L (2010) Microstructure and property control of advanced high strength automotive steel. In:Weng YQ, Dong H, Gan Y (eds) Metalluygical. Industry Press, Beijing, p 265 |
| 10. | Mclean D(1957) Grain boundaries in metals. Oxford , Clarendon Press |
| 11. | Sundman B, Jansson B, Andersson J(1985) The thermo-calc databank system. Calphad, 9(2), 153-190 doi:10.1016/0364-5916(85)90021-5 |
| 12. | Li L, Huang SG, Wang L, et al(2009) Thermodynamic reassessment of the Fe-Al-C system based on the Fe-rich experimental data. Front Mater Sci China, 3(1), 33-37 doi:10.1007/s11706-009-0014-3 |
| 13. | Redlich O, Kister AT(1948) Algebraic representation of thermodynamic properties and the classification of solutions. Ind Eng Chem, 40, 345-348 doi:10.1021/ie50458a036 |
| 14. | Sundman B, Ågren J(1981) A regular solution model for phases with several components and sublattices, suitable for computer applications. J Phys Chem Solids, 42(4), 297-301 doi:10.1016/0022-3697(81)90144-X |
| 15. | Kumar KCH, Raghavan V(1991) a thermodynamic analysis of the Al-C-Fe system. J Phase Equilib, 12(3), 275-286 doi:10.1007/BF02649916 |
| 16. | Gustafson P(1985) A thermodynamic evaluation of the Fe-C system. Scand J Metall, 14, 259 |
| 17. | Matlock DK, Speer JG (2009) Third generation of AHSS, microstructure design concepts. In:Haldar A, Suwas S, Bhattacharjee D (eds) Microstructure and texture in steels. Springer, New York, pp 185-205 |
| 18. | Li L, Gao Y, Shi W et al (2011) Martensite transformation in high Mn steels. HMnS2011, Soeal, Korea, p A19 |
| 19. | Olson GB, Cohen M(1976) A general mechanism of martensitic nucleation:Part Ⅱ. FCC→BCC and other martensitic transformations. Metall Trans A, 7A, 1905-1914 |
| 20. | Allain S, Chateau JP, Bouaziz O, et al(2004) Correlations between the calculated stacking fault energy and the plasticity mechanisms in Fe-Mn-C alloys. Mater Sci Eng A, 387-389, 158-162 doi:10.1016/j.msea.2004.01.059 |
| 21. | Dumaya A, Chateau JP, Allain S, et al(2008) Application of thermodynamics and kinetics in materials engineering. Mater Sci Eng A, 483-484, 184-187 doi:10.1016/j.msea.2006.12.170 |
| 22. | Inden G(1977) Determination of chemical and magnetic interchange and magnetic interchange energies in BCC alloys. Metallkde Z, 68, 529-534 |
| 23. | Hillert M, Jarl M(1978) A model for alloying in ferromagnetic metals. Calphad, 2, 227-238 doi:10.1016/0364-5916(78)90011-1 |
| 24. | Dinsdale AT(1991) SGTE data for pure elements. Calphad, 15, 317-425 doi:10.1016/0364-5916(91)90030-N |
 2016, Vol. 4
2016, Vol. 4