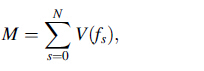The article information
- Zi-Yang Song, Yan-Li Zhang, Chi Wang, Wen-Wen Xu, Wei Ding
- Experimental measurement of acoustically induced surface vibration with different soil conditions
- Advances in Manufacturing, 2016, 4(3): 278-285.
- http://dx.doi.org/10.1007/s40436-016-0153-6
-
Article history
- Received: Jul. 16, 2015
- Accepted: Aug. 4, 2016
- Published online: Sep. 6, 2016
2 North Automatic Control Technology Research Institute, Taiyuan 030006, People’s Republic of China
3 Science and Technology on Near-Surface Detection Laboratory, Wuxi 214035, People's Republic of China
4 Shanghai Public Utility School, Shanghai, People's Republic of China
There is always a lack of well-structured theoretical system for the mechanism of acoustic-to-seismic (A/S) coupling due to the complexity of soils. The so-called A/S coupling means when the low-frequency sound wave below 1 kHz is incident from the air to the shallow surface, most of the sound wave energy will be reflected to the air due to the large acoustic impedance contrast between air and soil. However, because of the void of shallow surface, a lot of energy is coupled to the underground on account of momentum and viscosity friction between liquid soil and solid soil, which will induce various seismic waves, such as fast compressional wave (fast P-wave), slow compressional wave (slow P-wave) and shear wave [1-4]. Suppose there are something (e.g., landmine) buried under the ground, the seismic waves will be reflected to surface and cause changes in vibration state when meeting the buried land-mine on the condition of enough energy. Through detecting the changes of surface vibration, the existence of buried landmine can be further investigated [5, 6].
A/S coupling is an important theoretical basis for the method of acoustic buried landmine detection. The theory of A/S coupling has experienced a long period of devel-opment. In 1956, Biot [7, 8] established the two-phase porous medium theory, employing viscous dissipation mechanism to research seismic wave propagation charac-teristics. References [9-13] further developed the two-phase porous media theory of seismic wave propagation from different angles, helping to improve the accuracy of model and extend the objects of analysis. The soil is composed of solid, liquid and gas, and three-phase medium model can describe the propagation characteristics of seismic wave more accurately. Santos, et al. [14] derived Biot three-phase medium wave equations, showing that non-saturated porous medium has three types of compres-sion waves and a type of shear wave. Then, Beresnev et al. [15], studied seismic waves in the low-permeability volume.
Cai, et al. [16] investigated the effect of frequency and soil water saturation on attenuation of P-wave. Reference [17] analyzed the propagation characteristics of seismic wave in shallow soil, and did numerical analysis over the relationship between seismic wave propagation velocity and attenuation coefficient and relative parameters including sound frequency, soil porosity, soil water satu-ration, etc., which provides a theoretical basis for the investigation of the mechanism of A/S coupling. Using the method of scanning detection and analyzing the 3D dia-gram of surface vibration, we investigate the influence of soil properties on the signal characteristics of acoustically coupled surface vibration, which provides certain experi-mental basis for further research and application of the A/S coupling mechanism.
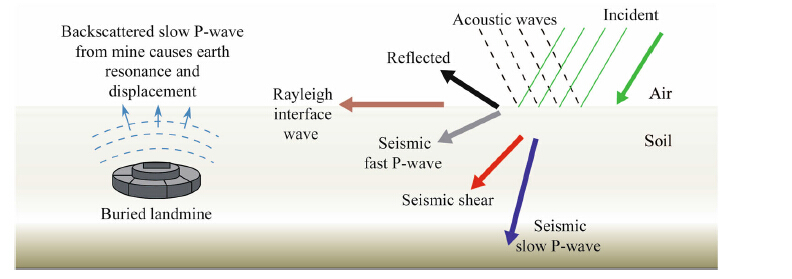
2 Theoretical basis of A/S coupling landmine detectionAccording to A/S coupling principle as shown in Fig. 1 which presented in Ref. [18], most of low-frequency acoustic waves that are incident upon soil are reflected back to air, but some other waves that are coupled under-ground excite seismic waves such as Rayleigh wave, fast P-wave, slow P-wave and shear wave. Intense reflection and scattering happen when slow P-wave traversing a landmine, but a great deal of wave energy loss occurs through diffusion. According to the existing research, fast P-wave energy has a small attenuation coefficient in the solid phase of soil, however a big attenuation coefficient in the fluid phase. Slow P-wave energy has a big attenuation coefficient in the solid phase of soil but a small attenuation coefficient in the fluid phase. Slow P-wave is highly diffuse in the process of transmission, and has a limited spread depth. Ultimately, the energy changing the surface vibra-tion state is weak and it is not enough to distinguish the existence of buried objects (e.g. landmines). However, landmines have a larger coefficient of acoustic compliance or flexibility relative to the soil, so they can constitute a "quality-spring" resonance system with the soil above and can eventually make the surface vibration change distinc-tively. On that basis, we can research the method for acoustic landmine discrimination. Because the buried objects such as bricks and roots, etc, do not have flexibility like landmines, they are not sensitive to the influence of surface vibration in the A/S coupling detection. Thus the technology of A/S coupling landmine detection boasts a strong ability of landmine identification.
|
| Fig. 1 Schematic diagram of acoustic-to-seismic coupling and resonance of landmine |
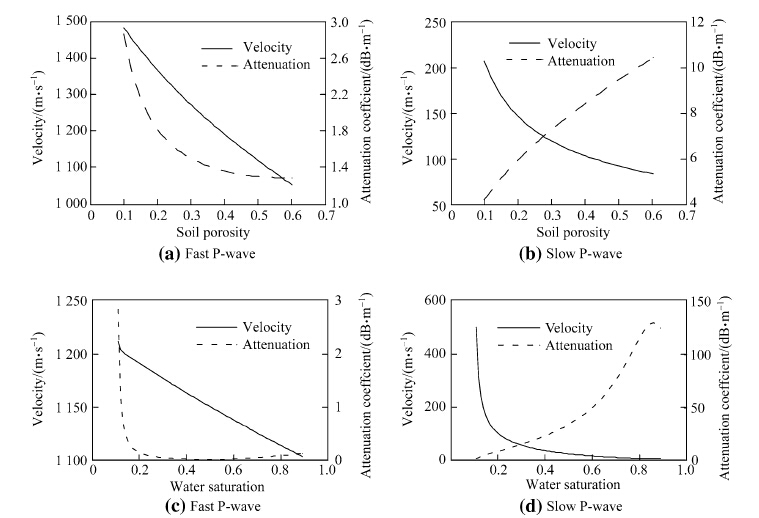
Propagation characteristics of acoustically coupled seismic waves are analyzed in the following. Shallow soil is a kind of three-phase medium consisting of solid phase, liquid phase and gas phase. According to A/S coupling principle, low-frequency acoustic wave can be coupled out of different components of seismic wave such as slow P-wave, fast P-wave, and shear wave when hitting the soil surface. Studies have shown that the longitudinal wave is mainly used in acoustic landmine detection. Here, the unsaturated three-phase porous elastic model can be adopted to analyze transmission characteristics of slow P-wave and fast P-wave. According to Ref. [17], the mathematical equations for velocity and attenuation coef-ficient of acoustically coupled fast P-wave and slow P-wave can be obtained, which are expressions about acoustic frequency and soil porosity, water saturation, bulk modulus, lame constant and other parameters. Figure 2 shows the influence of soil porosity and soil water satura-tion on fast and slow P-waves respectively presented in Ref. [17]. It can be seen that fast P-wave velocity is higher and decreases slightly with the increase of porosity and water saturation. The attenuation coefficient decreases with the increase of porosity and water saturation. However the overall attenuation coefficient is small. Slow P-wave velocity is relatively lower and decreases with the increase of porosity and water saturation. The attenuation coeffi-cient of slow P-wave is very large and increases with the increase of porosity and water saturation.
|
| Fig. 2 Influence of soil porosity and water saturation on characteristics of fast and slow P-waves |
According to the existing research, the fast P-wave energy has a small attenuation coefficient in the solid phase of soil, however a big attenuation coefficient in the fluid phase. Slow P-wave energy has a big attenuation coeffi-cient in the solid phase of soil but a small attenuation coefficient in the fluid phase. Soil solid phase has a density and an elastic modulus similar to those of the landmine body and their difference in characteristic impedance is relatively small. There is an obvious difference in charac-teristic impedance between the soil fluid phase and the landmine body. According to the fast and slow P-waves propagation characteristics, the fast P-wave energy is mainly concentrated in the solid phase of soil, and it makes less reflection or scattering energy when meeting the landmine because of the minor difference in acoustic impedance. As the slow P-wave energy is mainly concen-trated in the fluid phase of soil, it makes strong reflection or scattering energy when meeting the landmine because of the great difference in acoustic impedance and such energy will spread to the surface, changing its vibration velocity.
In the experiments of A/S coupling landmine detection, scanning sound waves from the low-frequency to high frequency are used to motivate the earth surface. It is noted that, the surface vibration signal is a combined effect of directly emitting acoustic waves, directly coupled and reflected seismic waves including shear wave, fast P-wave and slow P-wave, etc. In addition, the energy coupling efficiency of A/S coupling is very small due to the big acoustic impedance difference between the air and soil. In order to overcome and show the complex effect of surface vibration signal to be measured, referring to the solution method described in Refs. [19, 20], the surface vibration velocity is processed in this paper shown as follows: using the method of acoustic frequency sweeping, measure the amplitude-frequency characteristic curve of surface vibra-tion velocity at a certain position and sum the velocity in the range of frequency sweeping. The summed value M is the "vibration characteristic data" at the surface position to be tested and the unit is m/s. Mathematical expressions can be represented as
where f0, fN represent start frequency and stop frequency of scanning acoustic wave respectively, and V(fs) denotes the amplitude of surface vibration velocity when the excitation frequency is fs. X and Y coordinates are used to denote the measurement area. The values of "vibration characteristic" at all measurement points are used to denote the Z coordi-nate. Then we can get the 3D graph of surface vibration about the measured position, which can be used to reflect the characteristics of acoustically coupled surface vibra-tion. In the previous research, we explored the mechanism model of acoustic landmine detection. However, there is a lack of research on the influence of soil properties on the signal characteristic. In this paper, we analyze the effect of soil properties on the signal of A/S coupling by measuring the surface vibration intensity under different soil conditions.
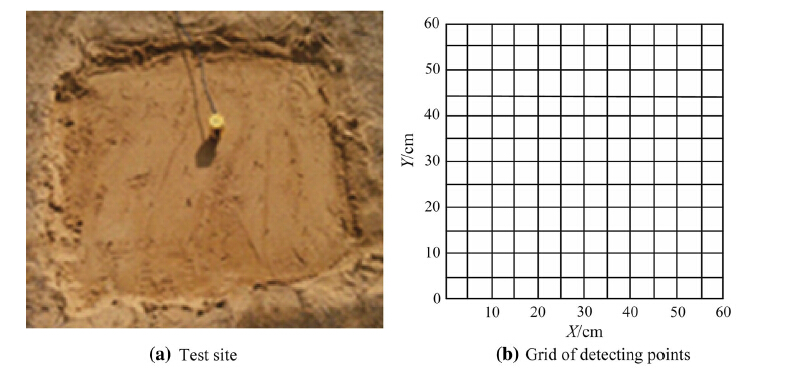
3 Experimental measuring schemeOn the basis of the principle of A/S coupling, we construct an experimental system which consists of an acoustic wave emitter, a surface vibration signal detector, and a data processing and analysis unit. The experimental system is shown in Fig. 3. The acoustic wave emitter is composed of a signal generator, a mixer, a power amplifier and a loud-speaker. The signal detector of soil surface vibration is composed of a geophone, a data acquisition card and a computer. The geophone collects time-domain signal of soil surface vibration and transfers it through the data acquisition card to computer for obtaining the frequency-domain features by the fast Fourier transform (FFT). The Tektronix AFG3022 arbitrary wave/function generator is used as the signal generator, and JB215 professional speakers produced by Soundking Group Co., Ltd. as the loudspeaker. Geophone is the product of Weihai Sunfull Electronics Group Co., Ltd., with a frequency response scope of 28-1 000 Hz. The model of data acquisition card is LDI320VSE. The experimental site is a bunker of the size 60 cm (length) 9 60 cm (width) 9 30 cm (depth) as shown in Fig. 4, and the experimental soil is ordinary sand. When a single landmine is used in the detection experi-ment, the landmine center and sandpit center should be overlapped with each other. With the scanning method as shown in Fig. 4, the sandpit is made into a lot of rectan-gular grids of 5 cm 9 5 cm, and all points are calibrated with abscissa and ordinate. In the experiment, the geo-phone is inserted into the measuring point for 7 cm deep. All points in the grid are scanned in turn.

|
| Fig. 3 Experimental system of A/S coupling |
|
| Fig. 4 Testing ground for acoustic landmine detection |
The loudspeaker produces sound waves of the acoustic pressure intensity about 120 dB. According to the existing experimental study, the signal energy of surface vibration excited by sound wave attenuates significantly with the increase of frequency. When the frequency is more than 400 Hz, the detected signals of surface vibration velocity are almost submerged by environmental noise. Therefore, we choose the frequency sweeping range of 50-400 Hz and conduct frequency sweeping detection every 1 Hz increased on the basis of 50 Hz. The sweeping detection results are transmitted into the computer for further ana-lyzing and processing, and we get the specific intensity-frequency characteristic curve accordingly. The vibration intensity Mxy at each point is calculated based on Eq.(1) and then we can get the 3D graph of surface vibration intensity relative to the measuring position. With the above experiment devices and measurement method, we study the influence of soil porosity and moisture on the acoustically induced surface vibration.
4 Results analysis and discussion 4.1 Test results under different porositiesFigure 5 shows the 3D graphs of surface vibration intensity under different porosities. Figure 5a is the sand physical figure for experimental use. Figures 5b-d refer to the 3D graphs of surface vibration intensity under the condition of large soil porosity, middle porosity and small porosity, respectively. Under the three porosities, the conditions such as sound source and soil humidity are the same. In Fig. 5b, the surface vibration intensity lies in 0.075-0.105 m/s. In Fig. 5c, the surface vibration intensity lies in 0.056-0.076 m/s. According to the results of Fig. 5, the surface vibration intensity lies in 0.048-0.058 m/s, and decreases with the decrease of soil porosity.
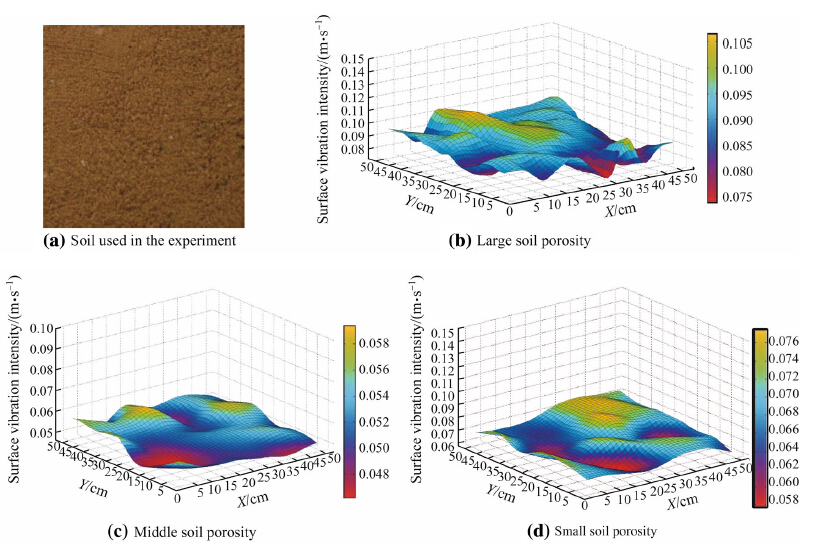
|
| Fig. 5 3D graphs of surface vibration intensity under different porosities |
Figure 6 shows the 3D graphs of surface vibration intensity under different porosities with a large plastic landmine buried. Figure 6a is the object graph of a large plastic landmine buried and the diameter of the buried landmine is 28 cm; Fig. 6b shows the 3D graph of surface vibration intensity under the normal soil condition when the buried depth of landmine is 16 cm in the case of large porosity. The value of surface vibration intensity in the landmine center is about 0.146 m/s. Figure 6c shows the 3D graph of surface vibration intensity when the depth of soil is compressed from 16 cm directly to 14 cm in the case of middle porosity. The value of surface vibration intensity in the landmine center is about 0.112 m/s. Figure 6d shows the 3D graph of surface vibration intensity when the depth of soil is compressed to 14 cm in the case of small porosity. The value of surface vibration intensity in the landmine center is about 0.096 m/s. Comparing Figs. 6b-d, we can see that the surface vibration intensity in the landmine center decreases as the soil porosity decreases. In addition, the raised part of the 3D graphs of surface vibration intensity is of the same size as the landmine. Comparing Figs. 5 and 6, it can be found that the surface vibration enhances significantly with a landmine buried.
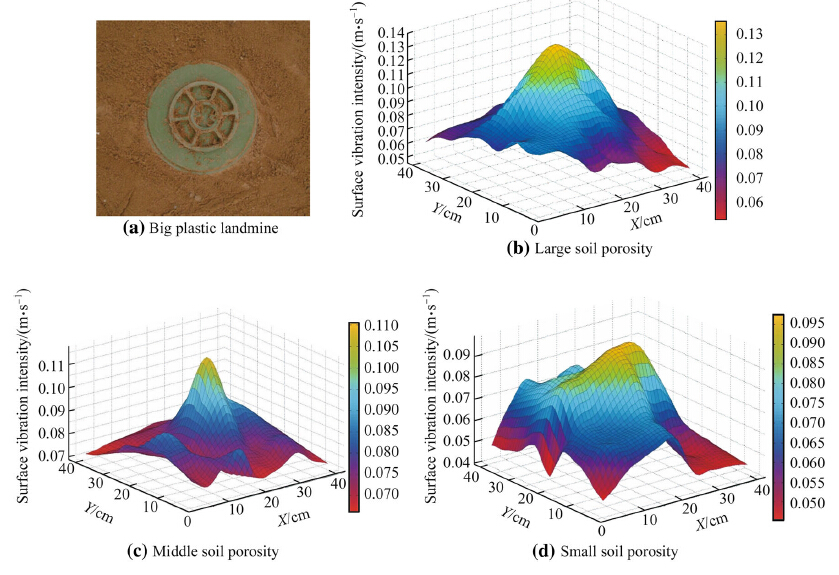
|
| Fig. 6 3D graphs of surface vibration intensity with landmine buried under different porosities |
Figure 7 illustrates the 3D graphs of surface vibration intensity under different soil moistures. Figure 7a presents the test soil. Figures 7b-d show the 3D graphs of surface vibration intensity under low, middle and high soil mois-tures. Based on Figs. 7b-d, the 3D graphs of surface vibration intensity are "plane", and the vibration velocity decrease with the increase of moisture. The maximum vibration intensity of soil surface is 0.105 9 10-3 m/s in the case of low moisture, 0.084 9 10-3 m/s in the case of middle moisture and 0.040 9 10-3 m/s in the case of high moisture.

|
| Fig. 7 3D graphs of surface vibration intensity under different moistures |
Figure 8 shows the 3D characteristic graph obtained in the experiment with a large plastic landmine buried under different soil moistures. Figure 8a shows the test soil, and Figs. 8b-d show the 3D graphs of surface vibration inten-sity under low, middle and high moistures. According to Figs. 8b-d, the influence of moisture on surface vibration intensity is not obvious. The peak surface vibration inten-sity is about 0.205 9 10-3 m/s in the case of low moisture, 0.198 9 10-3 m/s in the case of middle moisture and 0.1639 10-3 m/s in the case of high moisture. The raised part of the 3D graph of surface vibration intensity is of the same size of the landmine. The surface vibration intensity decreases a bit as the moisture increases. Comparing Figs. 7 and 8, the influence of the landmine on the acoustically induced surface vibration is great.
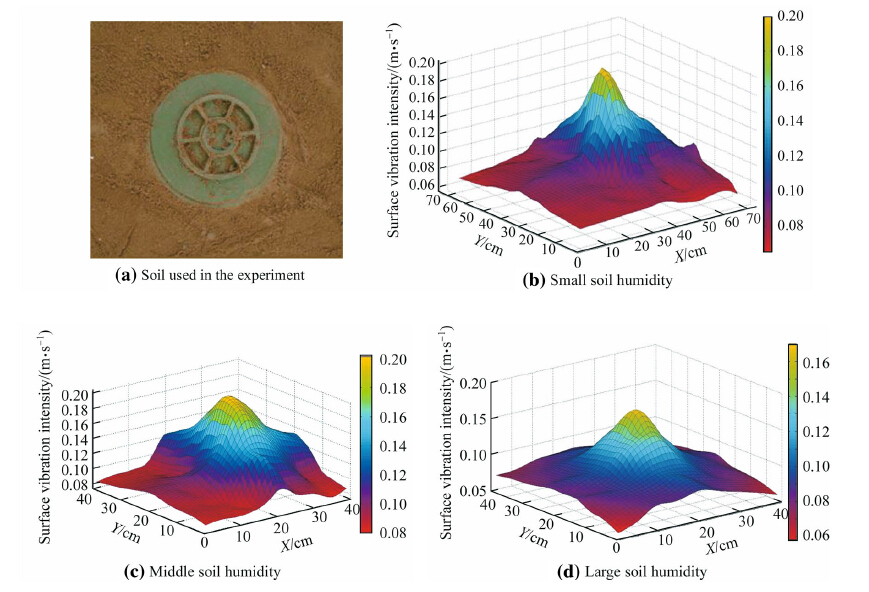
|
| Fig. 8 3D graphs of surface vibration intensity with landmine buried under different soil moistures |
Using the method of scanning detection and changing the soil properties, the detection signal of acoustically induced surface vibration can be visually analyzed. Through com-parative analysis of measured data with different soil porosities and moistures, we can draw the following con-clusions: (i) the decrease of surface vibration intensity is accompanied by the decrease of soil porosity and the increase of soil moisture; (ii) the influence of a buried landmine on the acoustically induced surface vibration is significant; (iii) the influence of soil property on the signal of A/S coupling landmine detection mainly depends on soil porosity and the landmine resonance, and the influence of soil moisture is not obvious under the given condition in this paper. With the obtained 3D characteristic diagrams, the critical factors which influence the signal of acoustic detection can be investigated with different soil conditions. The authors suggest that, using the 3D characteristic graph of surface vibration, the method can be further investigated to identify the location and dimension of buried landmine quickly. By combining the 3D characteristic graph of surface vibration with other techniques or systems, such as those described in Refs. [21-25], relevant issues can be explored in the future.
Acknowledgments The project is supported by the National Natural Science Foundation of China (Grant No. 61575119), and the Science and Technology on Near-Surface Detection Laboratory.| 1. | Bass HE, Bolen LN(1980) Coupling of airborne sound into the earth frequency dependence. J Acoust Soc Am, 67, 1502-1506 doi:10.1121/1.384312 |
| 2. | Sabatier JM, Bass HE, Bolen LN, et al(1986) The interaction of airborne sound with the porous ground:The theoretical formulation. J Acoust Soc Am, 79, 1345-1352 doi:10.1121/1.393662 |
| 3. | Sabatier JM, Bass HE, Bolen LN, et al(1986) Acoustically induced seismic waves. J Acoust Soc Am, 80, 646-649 doi:10.1121/1.394058 |
| 4. | Hickey CJ, Sabatier JM(1997) Measurements of two types of dilatational waves in an air-filled unconsolidated sand. J Acoust Soc Am, 102(1), 128-136 doi:10.1121/1.419770 |
| 5. | Sabatier JM, Xiang N(2001) An investigation of acoustic-toseismic coupling to detect buried antitank landmines. IEEE Trans Geosci Remote Sens, 39(6), 1146-1154 doi:10.1109/36.927429 |
| 6. | Xiang N, Sabatier JM(2003) An experimental study on antipersonnel landmine detection using acoustic-to-seismic coupling. J Acoust Soc Am, 113(3), 1333-1341 doi:10.1121/1.1543554 |
| 7. | Biot MA(1956) Theory of propagation of elastic waves in a fluidsaturated porous solid I:low-frequency range. J Acoust Soc Am, 28(2), 168-178 doi:10.1121/1.1908239 |
| 8. | Biot MA(1956) Theory of propagation of elastic waves in a fluidsaturated porous solid Ⅱ:higher frequency range. J Acoust Soc Am, 28(2), 179-191 doi:10.1121/1.1908241 |
| 9. | Dvorkin J, Nur A(1993) Dynamic poroelastic:a unified model with the squirt and the Biot mechanisms. Geophysics, 58(4), 524-533 doi:10.1190/1.1443435 |
| 10. | Stern M, Bedford A, Millwater HR(1985) Wave reflection from a sediment layer with depth-dependent properties. J Acoust Soc Am, 77(5), 1781-1788 doi:10.1121/1.391927 |
| 11. | Berryman JG(1981) Elastic wave propagation in fluid-saturated porous media. J Acoust Soc Am, 69(2), 416-424 doi:10.1121/1.385457 |
| 12. | Denneman AIM, Drijkoningen GG, Smeulders DMJ, et al(2002) Special section-seismic signatures of fluid transport dynamic effects of fluid:theory and modeling. Geophysics, 67(1), 282-291 doi:10.1190/1.1451800 |
| 13. | Mochizuki S(1982) Attenuation in partially saturated rocks. J Geophys Res Solid Earth, 87(B10), 8598-8604 doi:10.1029/JB087iB10p08598 |
| 14. | Santos JE, Douglas J, Corberó J, et al(1990) A model for wave propagation in porous medium saturated by a two-phase fluid. J Acoust Soc Am, 87(4), 1439-1448 doi:10.1121/1.399440 |
| 15. | Beresnev IA(2013) Seismic study of the low-permeability volume in southern France karst systems. Geophysics, 79(1), 1-13 |
| 16. | Cai YQ, Li BZ, Xu CJ(2006) Analysis of elastic wave propagation in sand stone saturated by two immiscible fluids. Chin J Rock Mech Eng, 25(10), 2009-2016 |
| 17. | Ding W, Wu WW, Wang C, et al(2014) Propagation characteristics of seismic waves in shallow soil with the unsaturated threephase poroelastic model. Acta Phys Sin, 63(22), 224301 |
| 18. | Robert WH, Kenneth DR(2005) Standoff acoustic laser technique to locate buried landmines. Linc Lab J, 15(1), 3-22 |
| 19. | Wang C, Li XF, Yu YJ, et al(2010) Analysis of soil-landmine resonance model. Acta Phys Sin, 59(9), 6319-6325 |
| 20. | Wang C, Zhou YQ, Shen GW, et al(2013) Numerical analysis of the resonance mechanisms of the lumped parameter system model for acoustic landmines detection. Chin Phys B, 22(12), 124601 doi:10.1088/1674-1056/22/12/124601 |
| 21. | Wang C, Zhou YQ, Shen GW, et al(2013) Impact of buried objects on acoustic-to-seismic coupling efficiency. J Tianjin Univ, 46(6), 498-502 |
| 22. | Ding W, Shen GW, Wang C, et al(2014) Acoustic-to-seismic coupling based discrimination for non-metallic mine detection. Optics Precis Eng, 22(5), 1331-1338 doi:10.3788/OPE. |
| 23. | Chen C, Liu D, Zhang HR, et al(2015) Application of equivalent circuit analysis method in investigation of acoustic resonance mines detection model. J Electron Meas Instrum, 29(6), 874-879 |
| 24. | Wang C, Xu LL, Zhu J, et al(2016) A novel integrated fiber-optic interferometer model and its application in micro-displacement measurement. Opt Lasers Eng, 86, 125-131 doi:10.1016/j.optlaseng.2016.05.012 |
| 25. | Ding H, Huang LL, Mao XY et al (2016) Primary resonance of traveling viscoelastic beam under internal resonance. Appl Math Mech (Engl Ed). doi:10.1007/s10483-016-2152-6 |
 2016, Vol. 4
2016, Vol. 4