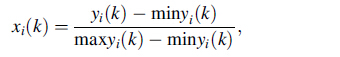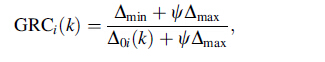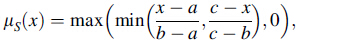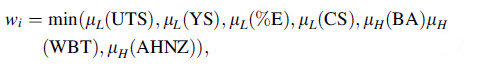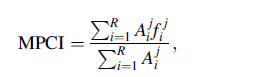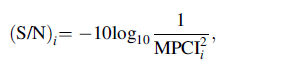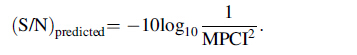The article information
- Prakash Kumar Sahu, Kanchan Kumari, Sukhomay Pal, Surjya K. Pal
- Hybrid fuzzy-grey-Taguchi based multi weld quality optimization of Al/Cu dissimilar friction stir welded joints
- Advances in Manufacturing, 2016, 4(3): 237-247.
- http://dx.doi.org/10.1007/s40436-016-0151-8
-
Article history
- Received: Jan. 25, 2016
- Accepted: Jul. 22, 2016
- Published online: Sep. 7, 2016
2 Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, Kharagpur, West Bengal 721302, India
Dissimilar joining of metals with different thermo-me-chanical and chemical properties is often more challenging as it results in formation of brittle intermetallic compounds. Joining of aluminum (Al) or its alloys with copper (Cu) is preferred in many applications in engineering as well as structural regime [1]. Dissimilar Al-Cu joint has appre-ciable weight reduction and widely used in industries like transportation, chemical, nuclear, aerospace and electronics [2]. However, fusion welding of Al alloys to Cu having melting point difference and high chemical affinity at elevated temperatures, induced residual stress, cracking and brittle intermetallic compounds (IMCs) in the weld zone, making it difficult to obtain good weld quality. To overcome the above mentioned drawbacks, the novel method, friction stir welding (FSW) process is expected to join dissimilar materials, such as Al with Cu [3].
FSW is an advanced solid state joining process. Initially, it was only used for welding Al alloys [4, 5], but now the research has been extended to a variety of materials like magnesium [6, 7], copper [8, 9], steels [10], titanium [11, 12] and composites [13]. The process is also used to joint dissimilar materials like aluminum of different grades [14, 15], magnesium to aluminum [16], steel to aluminum [17], copper to aluminum [18-21], etc. FSW process embroils joining of materials without melting the base materials and addition of filler materials. The welding is achieved through heating due to friction and severe mechanical deformation by a special rotating tool. Being a solid state joining technique it has a number of technical advantages such as smooth weld bead surface, less distor-tion and residual stress over conventional welding processes.
The joints’ quality depends on the welding parameters and can be assessed by the mechanical properties of the weld like ultimate tensile strength, yield strength, com-pressive strength, ductility, weld bead height and hardness. But the relation between the design variables to the quality characteristic parameters is highly complex, interdependent and non-linear. Therefore, to assure desired weld quality and reliability the selection of an optimal parameter setting is very essential. The conventional optimization techniques that can be implemented for determination of optimal FSW conditions are Taguchi method, factorial design, D-optimal design, response surface method, geometric programming, sequential unconstrained minimization technique, dynamic programming, etc. The recently developed non-conven-tional optimization techniques such as genetic algorithm, fuzzy logic, scatter search, artificial intelligence tech-niques, etc., can also be used. It has been observed that in most of these cases, a relationship between the process variables and responses is required to optimize the process parameters. But in most practical situation this relationship is nonlinear and complicated, which is difficult to be determined by using numerical and statistical techniques. Artificial intelligence techniques could be used in such cases but it requires a lot of experimental data. In recent years, Taguchi assisted methods are popularly used for process optimization.
The Taguchi technique is one of the most extensively used methods for optimization of control parameters for single output characteristic in FSW process [22-24]. In order to assess the control parameters, the Taguchi method uses signal-to-noise (S/N) ratio which is a logarithmic function of the desired output serving as objective function for optimization. It facilitates to understand the entire parameter space with nominal experimental runs [25]. The optimal control parameters settings provided by Taguchi method are robust against the variation of environmental conditions and other noise factors. However, the traditional Taguchi method cannot be implemented for multi-response optimization problem. But the real world problem relies on multi-response optimization which is not straightforward. It is highly complex than the single performance charac-teristic. Later on to optimize multi-response optimization problems, number of theories such as utility theory [26], grey relational theory [27] and desirability function approach [28] were coupled with the Taguchi method. These theories combine many quality attribute parameters into a single quality parameter which can be optimized using Taguchi method. However in such aggregation procedure, the relative importance/weight of each quality attribute parameter is required to be assigned [27, 28]. Assigning equal weight age to each quality parameter may not be a good decision. In practice, all the quality attributes of a product may not be of equal importance. The relative priorities are subjected to application area and functional requirements. Assigning different weights to each quality attribute depends on the judgment of the decision maker which may lead to uncertainty as well as indistinctness in the optimum solution. Moreover, aforementioned methods are based on the assumption that the quality characteristic parameters are uncorrelated. While in practice any change in one parameter remarkably affects the other parameter.
Recently, the fuzzy logic based approaches have been applied in many fields [29] to deal with the modeling, classification and control problems. This work therefore proposed a fuzzy based grey-Taguchi method for opti-mization of parameters setting in FSW process. Tool rota-tional speed (RPM), welding speed (WS), tool offset (TO) and plunge depth (PD) were considered as the controllable factors. Ultimate tensile strength (UTS), yield strength (YS), percentage elongation (%E), compressive strength (CS), bending angle (BA), weld bead thickness (WBT) and aver-age hardness at nugget zone (AHNZ) were considered as the weld quality parameters. The grey relational coefficients of these seven weld quality parameters were integrated into a multi-performance characteristic index (MPCI) in the fuzzy inference process. Then, the calculated MPCI values were used to determine the optimal levels of control parameters. Analysis of variance (ANOVA) was also performed to quantify the contribution of considered process parameters on the total variability. Microstructural analysis was also done to compare the grain size at various welded zones on both sides of the joint.
2 Fuzzy-grey-Taguchi method for optimization of process parametersFor the present research a fuzzy-grey-Taguchi method has been proposed for optimization of FSW process parameters with several weld quality features. The steps of the approach are shown in Fig. 1 and discussed as follows.
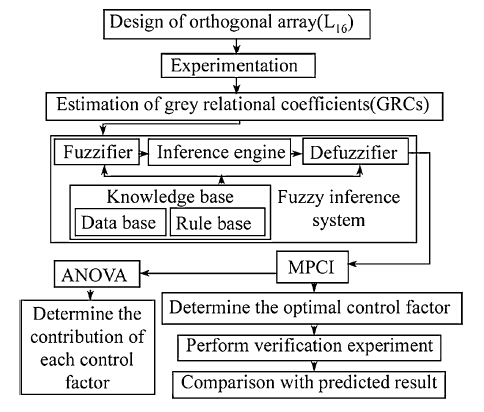
|
| Fig. 1 Flow chart of the proposed fuzzy-grey model |
The grey system theory, proposed by Deng in 1982, is mostly used for studying uncertainties in models and ana-lyzing relationships between systems [30]. This is an effective tool for studying the behavior of a system with inadequate and imperfect information. In grey relational analysis (GRA), normalization of experimental data between 0 and 1 is performed first. Based on the normal-ized data the grey relational coefficient (GRC) is computed to optimize the correlation between the ideal (best) and the actual normalized data.
2.1.1 Grey relational generationThe quality attributes of a process or product may have different ranges and units. Therefore, they need to be normalized to a common scale in order to compare them. In GRA, the data collected from the experiments, i.e., quality attributes, are normalized using three different criteria namely, higher-the-better (HB), lower-the-better (LB) and nominal-the-better (NB) according to the quality parame-ters of the process/product to be optimized [31, 32]. The criterion of HB is utilized if the objective is to maximize the quality parameter. In a welded joint the primary objective is to increase the strength, ductility, bending angle, weld bead thickness and hardness. In this work, all the considered weld quality parameters are maximized for stronger welded joint. Therefore, HB criterion is used to maximize the responses. Accordingly, the normalization of weld quality characteristics is performed using Eq. (1).
where xi(k) is the normalized value, yi(k) the kth quality parameter of the ith experiment, min yi(k) the minimum value of yi(k), and max yi(k) the maximum value of yi(k), i = 1, 2, 3, .. ., the number of experiments and k = 1, 2, 3, .. ., the number of responses.
2.1.2 Grey relational coefficientGRC represents the relationship between the reference sequence and compatibility sequence. The GRC can be obtained by using Eq. (2) [31, 32].
where GRCi(k) is the grey relational coefficient value of the kth response at the ith experiment;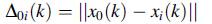
Fuzzy logic is an inexact reasoning based on fuzzy set theory. It provides mathematical tools to address the per-ception conveyed in natural language. Fuzzy system can represent human knowledge in the form of easily inter-pretable linguistic terms [33, 34]. The concepts of fuzzy sets and fuzzy algorithms were introduced by Zadeh in 1965 [33]. Mamdani and Assilian then extended the ideas into what became the fuzzy logic system [34]. After that, the fuzzy logic system has become one of the most active research topics in multidisciplinary area and has success-fully been applied in many industrial sectors. In this work, the optimization of process parameters based on a fuzzy inference process comprises of four main components, namely fuzzification, fuzzy rule base, fuzzy inference machine and defuzzification. A computer code for the proposed fuzzy inference system was developed using the C programming language. The fuzzy model used in this research is depicted in Fig. 1. All the steps are concisely described in the following sub-sections.
3.1 FuzzificationThe crisp values of parameters are converted into degrees of membership for linguistic terms of fuzzy sets in the fuzzification process. The membership function personifies the mathematical representation of membership value in a fuzzy set. All the input variables of the fuzzy inference system, i.e., grey relational coefficients of the measured weld quality parameters are divided into two linguistic terms or fuzzy levels, viz. low (L) and high (H) weld quality. The output of the inference system, i.e., multi-performance characteristic index (MPCI) is divided into six fuzzy levels, namely very low (VL), low (L), between low and medium (LM), between medium and high (MH), high (H) and very high (VH). The output of the fuzzification process is the degree of membership of element x in fuzzy set S. It is represented by lSj(xi), where the symbol lS(x) is the membership function. Its value lies in the interval (0, 1) that measures the degree to which element x belongs to the fuzzy set S, xi is the ith variable and Sj is the jth linguistic label or fuzzy set of the xi variable. In this research, tri-angular membership functions are used because of their simplicity and computational efficiency. The triangular membership function is identified by a set of three parameters {a, b, c} as Eq. (3)
where a and c (c >a) are feet of the triangle and b is the peak of the triangle. The membership functions of input and output parameters are depicted in Figs. 2 and 3, respectively.
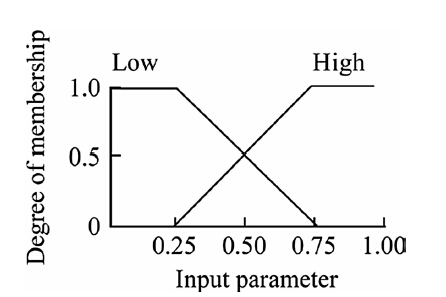
|
| Fig. 2 Membership functions of input parameters |
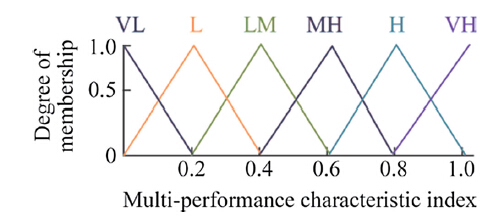
|
| Fig. 3 Membership functions of multi-performance characteristic index |
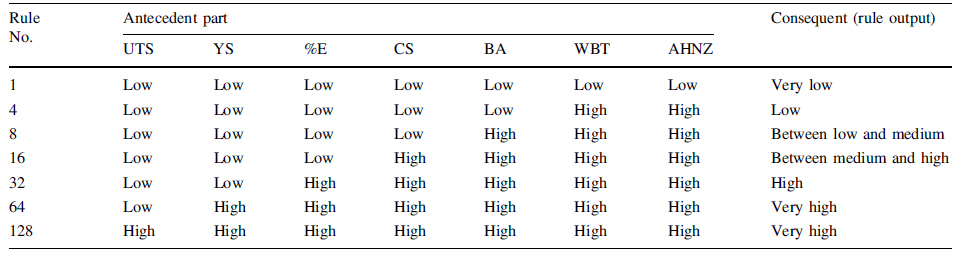
The complete comprehension of a system or process is retained as rules in the knowledge base. Fuzzy rule base consists of rules and each rule, in its turn, is obtained from properties expressed by linguistic variables and using logical connectives. It represents the relationships among the input and output variables. The rule base is essential to perform the inference operation. Actually, the use of linguistic parameters and if-then rules exploits the tolerance for imprecision and uncertainty. Usually, if-then rules are subjectively specified by humans who are experienced and knowledgeable in the problem. A fuzzy if-then rule (ith rule) can be expressed as
i.e., from the above rule Eq. (4) it can be said that if UTS, YS, %E and CS all these quality parameters belong to fuzzy set low and BA, WBT and AHNZ belong to fuzzy set high then the MPCI belongs to the fuzzy set between low and medium. In this rule the conditions of the if part must be met simultaneously for the result of the then part to occur. The fuzzy rules are obtained from the belief that the higher the GRC is, the better is the MPCI value. The conditions of the IF part of the rules are connected by fuzzy and operator. Because to produce good weld joints, all the quality characteristics parameters viz., ultimate tensile strength, yield strength, percentage elongation, compres-sive strength, bending angle, weld bead thickness and average hardness at nugget zone, have to be the maximum simultaneously. In the fuzzy inference system, there are seven input parameters and two fuzzy subsets for each parameter. Therefore, a total of 27, i.e., 128 rules are derived. Few rules are shown in Table 1. The complete rule base is available at www.iitg.ernet.in/spal/Rule_Base_PS. pdf.
Fuzzy inference is referred as fuzzy reasoning or approximate reasoning. It evaluates the outcome of a fuzzy rule using the given input information. For instance, the output of the rule in Eq. (4) after inference operation is given by where wi is called the firing strength of the ith rule.
3.4 DefuzzificationDefuzzification or aggregation of rules outputs is a math-ematical process by which the fuzzy sets are combined into a single real number or crisp value. In this work, centre of gravity method is adopted in the defuzzification process. The defuzzification value, called a multi-performance characteristic index, was calculated by using Eq. (6).
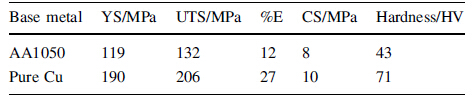
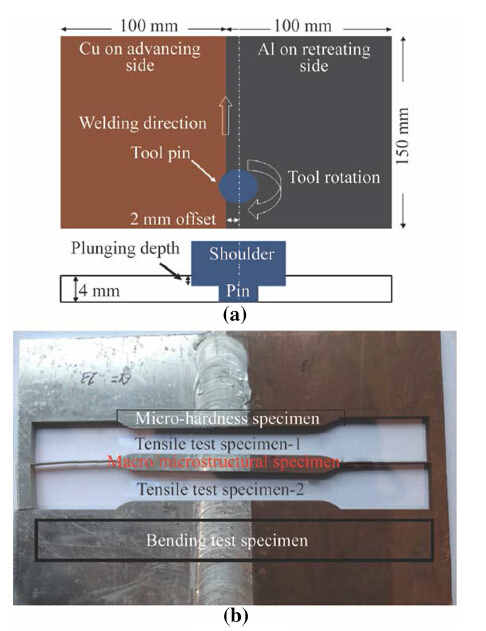
4 ExperimentationIn the present work the workpiece materials used are 1050 aluminum alloy (AA1050) and pure Cu plates with dimension of 150 mm 9 100 mm 9 4 mm to get square butt joint in a single pass. The chemical composition, in weight percentage of the Al plate, is the Al (99.50%), Si (0.25%), Fe (0.40%), Zn(0.07%) and Cu, Mg, Ti, Mn each of 0.05% and copper plate is 99.94% Cu and 0.02% Ag. The mechanical properties of the Al and Cu plates are given in Table 2. The plates were properly positioned and mechanically clamped by using a special fixture. In FSW process the plasticized material flow from the advancing side to the retarding side. Therefore, Cu and Al plates were placed on the advancing and retarding sides, respectively, as the hardest material has to flow inside the softest one. Moreover, higher heat is generated on the advancing side. The welding process was started by plunging the tool pin with varying tool offset of 0.5-2 mm. The tool offset is the distance between the interface of the plates to be welded and the center of the tool pin and plunging depth is the amount of penetration of the tool shoulder into the work-piece material, as shown in Fig. 4a. A non-consumable tool made of H13 tool steel with shoulder diameter of 25 mm, pin diameter of 6 mm, pin length of 3.5 mm and cylindrical pin profile were used for all the experiments. Shorter pin length was considered (optimized by trial experiment) to avoid rubbing of the tool pin due to plunge depth and sticking of plasticized material on the backing plate. The welding experiments were performed in a CNC FSW machine (Model No.:2T; Make: ETA technology Pvt. Ltd.) which has maximum tool rotational speed of 3 000 r/min and welding speed of 1 000 mm/min.
|
| Fig. 4 a Tool offset and plunging depth scheme, b scheme of extraction of specimen from FSW plate |
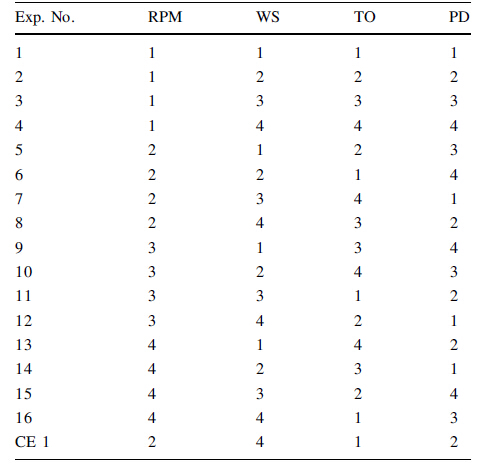
The two important points that should be considered before selecting an OA for DOE are the number of control parameters and their levels. There are large numbers of process parameters which can control the quality of FSWed joint. Some preliminary experiments were conducted for selecting important parameters and their ranges. Four welding parameters namely, tool rotation speed, welding speed, tool offset and plunge depths were considered in this investigation. To explore the effect of the considered process parameter comprehensively the number of levels of each parameter was considered as four. Therefore, Taguchi’s L16 OA was adapted in this work. The levels of parameters and the design matrix are shown in Table 3 and 4, respectively.
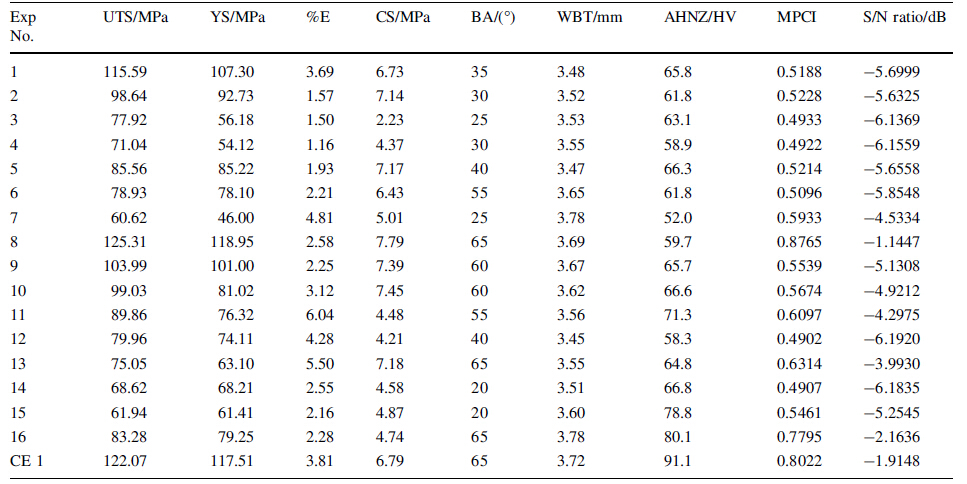
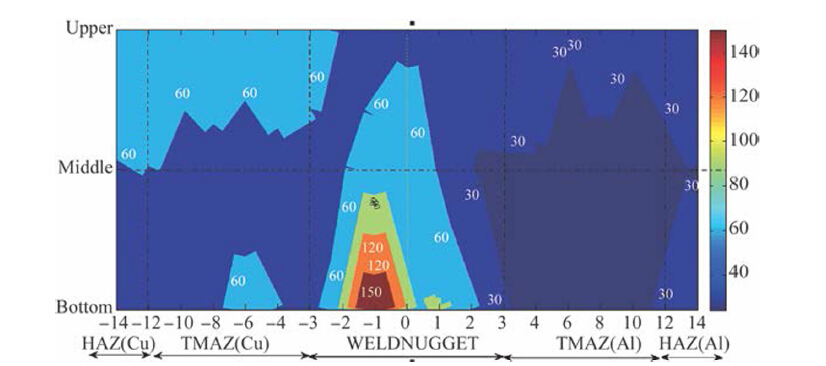
After completion of the experiment, specimens were prepared for mechanical testing. From each experimental condition two tensile test specimens, one compressive/bending test and one micro-hardness test and one microstructural analysis specimen were extracted as per the diagram shown in theFig. 4b . The average of the two tensile test results has been considered for analysis. The weld quality characteristics or output responses, namely UTS, YS, %E, CS, BA, WBT and AHNZ were measured for each case. Tensile test was conducted on an INSTRON-Dynamic UTM machine (Model 8801) as per the guide lines of American Society for Testing of Mate-rials (ASTM E8). A 50 mm gauge length was considered to measure the percentage of elongation and the bending angle was measured by 3 point bending test setup con-nected to the UTM. For micro-hardness test the specimens were polished by using 200, 400, 600, 800, 1 000, 1 500 grade emery paper and hardness was measured by Vicker microhardness indentation machine at 500 g force with 10 s dwell time. Micro-hardness values were measured at three different layers namely, upper, middle and bottom layers along the cross section. In each specimen, a total of 60 hardness readings were taken. The tensile, bending, hard-ness specimens and hardness profile are shown in Figs. 5-8. For relevant metallographic observation the specimen was taken in such a manner that it includes the base material (BM), heat affected zone (HAZ), thermo-me-chanical affected zone (TMAZ) and nugget zone (NZ). The measured weld quality values are given in the Table 5.

|
| Fig. 5 Macrograph of failed tensile specimen |

|
| Fig. 6 a Macrograph of the bending tested specimen, b 3 Point bending test setup |

|
| Fig. 7 Micro-hardness tested specimen |
|
| Fig. 8 Micro-hardness tested sample profile |
Hardness values of different layers were measured for all the specimens. The number of graphical results obtained is quite large with many of them showing similar characteristics. Hence, only the representative profile is shown in Fig. 8. From the hardness profile it was observed that the hardness at the NZ is higher as compared to all other zones. This may be due to the formation of inter-metallic compounds and finer grain at the joint. It was also observed that the hardness at the bottom layer is more compared to the other layers due to the high cooling rate of the bottom part which is in directly contact with the backing plate. The variation of the hardness in the NZ (45-150 HV) is not uniform. This may be due to mechanically stirring and mixing of Al and Cu in the weld nugget forming partially intermetallic compounds and pure Al/Cu getting preserved in the respective regions.
5 Selection of optimal parameters settingAll the experimental outputs given in Table 5 were nor-malized by using Eq. (1) and the GRC of the corresponding data were computed from Eq. (2). These GRC values were used as inputs to the fuzzy inference process for calculation of MPCI values. The membership values of each of the input parameters in different fuzzy sets were determined by using Eq. (3), then the fuzzy rules were evaluated in fuzzy infer-ence system and finally the MPCI values were calculated by using Eq. (6) in the defuzzification process. This completes the overall representation of all the quality parameters. Thus, the multi-criterion optimization problem has been transferred into a single equivalent objective optimization problem by using the combination of grey relational analysis and fuzzy inference system. The S/N ratios of MPCI values were cal-culated by following HB criterion by using Eq. (7) [27].
where (S/N)i is the S/N ratio of the ith experiment and MPCIi is the MPCI value of the ith experiment. The MPCI values obtained by using the experimental data and the calculated S/N ratios (using Eq. (7)) are shown in Table 5.
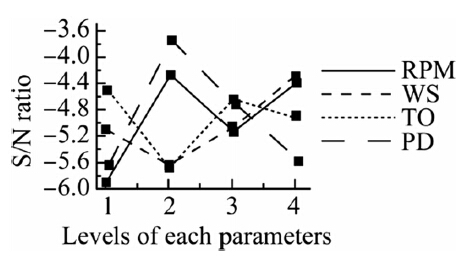
In OA experimental design, it is possible to disperse the influence of individual control parameter at different levels by averaging the responses of the corresponding levels. The mean S/N ratios of the MPCI values at levels for each process parameter were computed and plotted in Fig. 9. Irrespective of the quality attributes selected for a given response, a higher S/N ratio correlates superior quality. Hence, the optimum level of the control parameters is the level which confirms the highest S/N ratio. Depending on the S/N ratio analysis as shown in Fig. 9, the optimum parametric combination for this multi-objective optimization problem is found to be at levels 2, 4, 1 and 2 of factors tool rotational speed, welding speed, tool offset and plunging depth, respectively.
|
| Fig. 9 Main effects response plot of S/N ratio for MPCI |
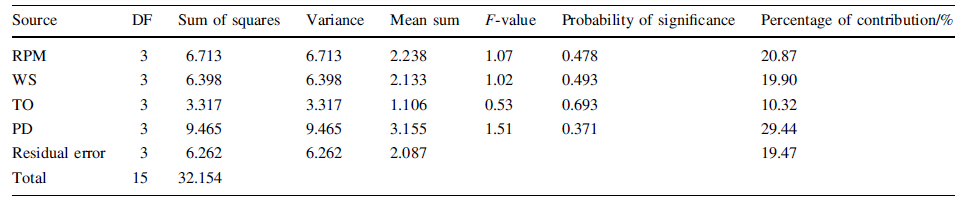
The ANOVA is a collection of statistical models for recognition of the effects of individual control parameter on the quality attributes. The effect of control parameters on the S/N ratios of the MPCI values was calculated and given in Table 6. It is observed that plunge depth is the most impacting parameter with 29.44% contribution and least influencing parameter is tool offset with 10.32% contribution. It is also found that the considered parameters can only explained 80.53% of the total variability. The contribution of residual error is 19.47% this is due to the interaction effects of the design parameters which were not considered separately in this analysis.
Once the optimal levels of the design parameters have been selected, the final step of the Taguchi method is to verify the improvement of the quality characteristic by using the optimal parameter settings. A confirmation experiment was carried out by using the optimal parameter combinations. The predicted S/N ratio, by using the optimal level of the design parameters is calculated using Eq. (8).where (S/N)m is the mean S/N ratio of all the experimental runs; (S/N)i is the mean S/N ratio at the optimal level of the ith parameter; F is the number of design parameters.Therefore, the predicted S/N ratio can be used to calculate the MPCI value using Eq. (9).
The predicted optimal S/N ratio and MPCI values were found as -1.672 dB and 0.8249 using Eqs. (8) and (9) respectively. A validation experiment was performed using optimal parameter setting, shown in Table 4 (Exp. No. CE1), and the measured weld quality values with MPCI value and S/N ratio are given in Table 5. The improvement was not observed in the experimental data. This could be due to the experimental errors and interaction effects of the design parameters which were not considered in this analysis.
7 Microstructural analysisFor microstructural analysis, specimens were taken nor-mal to the direction of welding and polished with coarser to finer emery paper (200, 400, 600, 800, 1 000, 1 200, 1 500, 2 000 grade emery paper) followed by velvet polishing to get scratch free mirror finish surface. After polishing Al part was etched with modified Keller’s reagent and the Cu part was etched with 5 g of FeCl3 with 50 mL of HCl and 50 mL of distilled water. The microstructures of various welded zones of all the 17 specimens were studied in an upright optical microscope (Model: Axiotech). The number of microstructures obtained at different zones for all the specimens is quite large with many of them showing similar characteristics. Hence, only the representative photographs of the Exp. No. 8 for all three welded zones viz. HAZ, TMAZ and NZ with base materials are presented in Figs. 10a-h. Figures 10 b, d, f and h show the microstructure of the HAZ, TMAZ and NZ zone at the Cu side. Microstruc-tural analysis reveals that the grain size of the Cu base material is very large as compared to all other zones. This may be due to crystal type structure of the base material. The crystal arrangement is not uniform due to rolling of the sheet. After the FSW process the grains are intermixed and the boundary of the grains is not very clear. This may be due to the stirring action of the tool and also the heating effect of the process. The grain size became coarse to finer from the base material to the center of the weld (i.e., NZ). The NZ grain at Cu side is finer due to stirring effect of the tool and dynamic recrystallization.

|
| Fig. 10 Microstructure and grain size of Exp. 8 at the a Al base material, b Cu base material, c HAZ of Al, d HAZ of Cu, e TMAZ of Al, f TMAZ of Cu, g NZ of Al, h NZ of Cu |
Similar changes of microstructure were also observed in the Al side (see Figs. 10a, c, e) and g. The base material grain size of Al alloy is higher than all the zones. From the base material to the center of the weld the size of the grains were decreased due to the stirring effect of the tool which is previously explained for the Cu side. But at the Al side it has not much effect due to softer and low melting tem-perature of pure Al material compared to Cu material.
8 ConclusionsTo optimize the welding process parameters for dissimilar Al/Cu joint using FSW process, fuzzy assisted grey Taguchi method was applied in this investigation. The seven weld quality parameters were converted into a combined quality variable by multi-performance charac-teristic index which was used as a cost function for opti-mization. Taguchi L16 OA was adopted to perform the welding experiments. It is found from the ANOVA anal-ysis that the plunging depth and tool rotational speed can explain almost 50% of the total variance of the process and tool offset is the least contributing parameter with 10.32% contribution. Based on the S/N ratio analysis it is found that combination of higher level of welding speed and lower levels of other parameters give better weld quality. The analysis shows that the proposed hybrid fuzzy-grey Taguchi approach is suitable for optimizing the FSW process. The accuracy of the proposed approach may be improved further by increasing number of fuzzy sets. Moreover, the expert knowledge and experience can be integrated in the rule base.
Acknowledgement This work is supported by Department of Mechanical Engineering, Indian Institute of Technology Guwahati.| 1. | Al-Roubaiy AO, Nabat SM, Batako ADL(2014) Experimental and theoretical analyses of friction stir welding of Al to Cu joints. Int J Adv Manuf Technol, 71, 1631-1642 doi:10.1007/s00170-013-5563-z |
| 2. | Genevois C, Girard M, Huneau B, et al(2011) Interfacial reaction during friction stir welding of Al and Cu. Min Met Mater Soc, 42, 2290-2295 |
| 3. | Liu HJ, Shen JJ, Zhou L, et al(2011) Microstructural characterisation and mechanical properties of friction stir welded joints of Al to Cu. Sci Technol Weld Join, 16(1), 92-99 doi:10.1179/1362171810Y.0000000007 |
| 4. | Thomas WM, Nicholas ED, Needham JC et al (1991) Friction stir welding. International Patent Application No. PCT/GB92/02203 and Great Britain Patent Application No. 9125978.8 |
| 5. | Vidal C, Infante V, Vilaca P(2010) Assessment of improvement techniques effect on fatigue behaviour of friction stir welded aerospace aluminium alloys. Proc Eng, 2, 1605-1616 doi:10.1016/j.proeng.2010.03.173 |
| 6. | Sahu PK, Pal S(2015) Multi-response optimization of process parameters in friction stir welded AM20 magnesium alloy by Taguchi grey relational analysis. J Magnes Alloys, 3, 36-46 doi:10.1016/j.jma.2014.12.002 |
| 7. | Padmanaban G, Balasubramanian V, Sarin Sundar JK(2010) Influences of welding processes on microstructure, hardness, and tensile properties of AZ31B magnesium alloy. J Mater Eng Perform, 19, 155-165 doi:10.1007/s11665-009-9389-7 |
| 8. | Fattah-alhosseini A, Taheri AH(2015) Effect of friction stir welding on corrosion behavior of pure copper in 3.5 wt% NaCl solution. J Manuf Process, 20, 98-103 doi:10.1016/j.jmapro.2015.09.005 |
| 9. | Lina J, Changa H, Wu M(2014) Comparison of mechanical properties of pure copper welded using friction stir welding and tungsten inert gas welding. J Manuf Process, 16, 296-304 doi:10.1016/j.jmapro.2013.09.006 |
| 10. | Baraka A, Panoutsos G, Cater S(2015) A real-time quality monitoring framework for steel friction stir welding using computational intelligence. J Manuf Process, 20, 137-148 doi:10.1016/j.jmapro.2015.09.001 |
| 11. | Seighalani KR, Givi MKB, Nasiri AM, et al(2010) Investigations on the effects of the tool material, geometry, and tilt angle on friction stir welding of pure titanium. J Mater Eng Perform, 19, 955-962 doi:10.1007/s11665-009-9582-8 |
| 12. | Sanders DG, Ramulu M, Klock-McCook EJ, et al(2008) Characterization of super plastically formed friction stir weld in titanium Al-4V:preliminary results. J Mater Eng Perform, 17, 187-192 doi:10.1007/s11665-007-9186-0 |
| 13. | Uzun H(2007) Friction stir welding of SiC particulate reinforced AA2124 aluminium alloy matrix composite. Mater Des, 28, 1440-1446 doi:10.1016/j.matdes.2006.03.023 |
| 14. | Leitao C, Emílio B, Chaparro BM, et al(2009) Formability of similar and dissimilar friction stir welded AA 5182-H111and AA 6016-T4 tailored blanks. Mater Des, 30, 3235-3242 doi:10.1016/j.matdes.2008.12.005 |
| 15. | Grujicic M, Arakere G, Yen CF, et al(2011) Computational investigations of hardness evolution during friction stir welding of AA5083 and AA2139 aluminum alloys. J Mater Eng Perform, 20, 1097-1108 doi:10.1007/s11665-010-9741-y |
| 16. | Mofid MA, Abdollah-zadeh A, Ghaini FM(2012) The effects of water cooling during dissimilar friction stir welding of Al alloy to Mg alloy. Mater Des, 36, 161-167 doi:10.1016/j.matdes.2011.11.004 |
| 17. | Movahedi M, Kokabi AH, Seyed-Reihani SM, et al(2013) Effect of annealing treatment on joint strength of aluminum/steel friction stir lap weld. Mater Des, 44, 487-492 doi:10.1016/j.matdes.2012.08.028 |
| 18. | Sahu PK, Pal S, Pal SK, et al(2016) Influence of plate position, tool offset and tool rotational speed on mechanical properties and microstructures of dissimilar Al/Cu friction stir welding joints. J Mater Process Technol, 235, 55-67 doi:10.1016/j.jmatprotec.2016.04.014 |
| 19. | Bisadi H, Tavakoli A, Tour SM, et al(2013) The influences of rotational and welding speeds on microstructures and mechanical properties of friction stir welded Al5083 and commercially pure copper sheets lap joints. Mater Des, 43, 80-88 doi:10.1016/j.matdes.2012.06.029 |
| 20. | Akinlabi ET(2012) Effect of shoulder size on weld properties of dissimilar metal friction stir welds. J Mater Eng Perform, 21, 1514-1519 doi:10.1007/s11665-011-0046-6 |
| 21. | Carlone P, Astarita A, Palazzo GS, et al(2015) Microstructural aspects in Al-Cu dissimilar joining by FSW. Int J Adv Manuf Technol, 79, 1109-1116 doi:10.1007/s00170-015-6874-z |
| 22. | Vidal C, Infante V(2013) Optimization of FS welding parameters for improving mechanical behavior of AA2024-T351 joints based on Taguchi method. J Mater Eng Perform, 22(8), 2261-2270 |
| 23. | Rao TB, Gopala Krishna A(2013) Simultaneous optimization of multiple performance characteristics in WEDM for machining ZC63/SiCp MMC. Adv Manuf, 1, 265-275 doi:10.1007/s40436-013-0029-y |
| 24. | Shojaeefard MH, Khalkhali A, Akbari M, et al(2013) Application of Taguchi optimization technique in determining aluminum to brass friction stir welding parameters. Mater Des, 52, 587-592 doi:10.1016/j.matdes.2013.06.003 |
| 25. | Taguchi G (1986) Introduction to quality engineering:designing quality into products and processes. Kraus International Publications, New York |
| 26. | Walia RS, Shan HS, Kumar P(2006) Multi-response optimization of CFAAFM process through taguchi method and utility concept. Mater Manuf Proc, 21, 907-914 doi:10.1080/10426910600837814 |
| 27. | Pal S, Malviya S, Pal SK, et al(2009) Optimization of quality characteristics parameters in a pulsed metal inert gas welding process using grey-based Taguchi method. Int J Adv Manuf Technol, 44, 1250-1260 doi:10.1007/s00170-009-1931-0 |
| 28. | Karande P, Gauri SK, Chakraborty S(2013) Applications of utility concept and desirability function for materials selection. Mater Des, 45, 349-358 doi:10.1016/j.matdes.2012.08.067 |
| 29. | Tiwary AP, Pradhan BB, Bhattacharyya B(2014) Application of multi-criteria decision making methods for selection of microEDM process parameters. Adv Manuf, 2, 251-258 doi:10.1007/s40436-013-0050-1 |
| 30. | Julong D(1989) Introduction to grey system theory. J Grey Syst, 1, 1-24 |
| 31. | Datta S, Bandyopadhyay A, Pal PK(2008) Grey-based Taguchi method for optimization of bead geometry in submerged arc bead-on-plate welding. Int J Adv Manuf Technol, 39, 1136-1143 doi:10.1007/s00170-007-1283-6 |
| 32. | Kasman S(2013) Multi-response optimization using the Taguchibased grey relational analysis:a case study for dissimilar friction stir butt welding of AA6082-T6/AA5754-H111. Int J Adv Manuf Technol, 68, 795-804 doi:10.1007/s00170-012-4720-0 |
| 33. | Zadeh LA(1965) Fuzzy sets. Inf Control, 8, 338-353 doi:10.1016/S0019-9958(65)90241-X |
| 34. | Mamdani EH, Assilian S(1975) An experiment in linguistic synthesis with a fuzzy logic controller. Int J Man-Machine Stud, 7, 1-13 doi:10.1016/S0020-7373(75)80002-2 |
 2016, Vol. 4
2016, Vol. 4