The article information
- Lei Wang, Jing-Cao Cai, Ming Li
- An adaptive multi-population genetic algorithm for job-shop scheduling problem
- Advances in Manufacturing, 2016, 4(2): 142-149
- http://dx.doi.org/10.1007/s40436-016-0140-y
-
Article history
- Received: 8 October 2015
- Accepted: 27 April 2016
- Published online: 7 June 2016
The scheduling problems,as important and well known problems,are hot issues in planning and managing manufacturing system. The job-shop scheduling problem (JSP) is one of the most typical and difficult problems in this area [1]. The JSP can be described as follows: there are n different jobs to be processed on m different machines. All the operations of each job are processed in a pre-determined processing sequence. Each operation is characterized by required machine with the fixed machining time. All machines are available at time zero and all jobs can also be processed at time zero. As one of the existing combinatorial optimization problems,the JSP has been proved to be a well-known NP-hard problem [2, 3, 4],and has also been demonstrated to be computationally challenging. It is not easy to develop a perfect approach for finding a good solution within a reasonable time even for small and moderate instances [2, 5]. For instance,the optimal solution of the well-known JSP benchmark problem FT10 had not been found until several decades after the problem was originally proposed [2]. Recently,the metaheuristics algorithms have been employed to deal with JSP by many scholars,such as genetic algorithm (GA) [6, 7, 8, 9],tabu search method [10, 11],particle swarm optimization [5, 12],ant colony optimization [13],and simulated annealing (SA) [14]. In this paper,we develop an improved GA in order to obtain better optimization result for JSP.
In the early 1970s,GA was originally developed by Holland,and it has been applied to many complex search problems. GA has shown a good optimization performance because of its global searching ability. A lot of successful GA applications for JSP have been appearing [15, 16, 17]. However,the traditional GAs for JSP usually have a slow convergence speed,and they are easy to fall into local optimal solutions far from the satisfied solution. Therefore,some improved or hybrid GAs are proposed to overcome those disadvantages. Liu et al. [18] used a method of combining the Taguchi method which could exploit the optimal offspring,with the traditional GA which had a powerful global searching capability to deal with JSP. A hybrid GA was proposed by Ahmadizar and Farahani [19] for open shop scheduling problem to minimize the makespan. Computational results showed that the proposed algorithm outperformed other GAs and was very competitive with well-known heuristic methods. An enhanced GA was proposed by Wang and Zheng [20] to deal with JSP. An effective crossover operator for operation-based encoding was used to avoid unfeasible solutions which were decoded into active schedules during the search process. Watanabe et al. [9] used a GA with modified crossover operator and adaptive searching area for JSP. Zhang et al. [21] developed an effective method by combining GA with SA to solve JSP. Based on a new neighborhood structure evaluation method,Gao et al. [2] used a hybrid algorithm for JSP. Gao et al. [17] designed an efficient hybrid memetic algorithm,with a novel local search to deal with JSP. Zhang et al. [22] proposed a hybrid GA based on a local search heuristic for JSP. A hybrid parallel micro GA was used to deal with JSP by Yusof et al. [23]. Ren and Wang [24] proposed a hybrid GA for finding the critical path from schedule and a local search operator. Lei and Guo [25] used an effective neighborhood search for scheduling in dual resource constrained interval job shop with environmental objective. A new hybrid island model GA for JSP was proposed by Kurdi [26]. A new naturally inspired migration selection mechanism and a new naturally inspired evolution model were proposed in order to avoid falling into the premature convergence and improve the search diversification [27]. An agent-based parallel GA for JSP was proposed to create the initial population,and the simulation results on benchmark instances indicated that the proposed algorithm could improve the efficiency [28].
Based on above survey,we also propose an effective adaptive multi-population genetic algorithm (AMGA) to minimize makespan for JSP. Our work differs from the existing ones at least in three aspects. Firstly,a multipopulation is proposed to minimize makespan for JSP. The second is to design novel adaptive crossover probability and mutation probability,because the crossover probability and mutation probability are necessary for GA to control its search performance. The third is that the elite individuals are evolved directly to the next generation in order to get a better solution for JSP.
2 JSP modelThere are several constraints on jobs and machines: (i) the operations of different jobs have no precedence constraints; (ii) a job only visits one machine for once; (iii) each machine can process only one job at a time; (iv) operations cannot be interrupted; (v) neither due dates nor release times are specified [6, 29]. The problem is to determine the operation sequences on the machines in order to minimize the makespan—that is the time required to complete all jobs. Therefore,the model for JSP can be defined as follows:
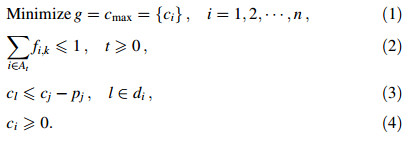
The objective function g in Eq. (1) is to minimize makespan that is the completion time of the last processing operation. Equation (2) indicates that each job is only processed by one machine at a time and each machine can only process at most one job at a time. Equation (3) shows the constraint of precedence relationship. Finally,Eq. (4) indicates that the finish time must be nonnegative.
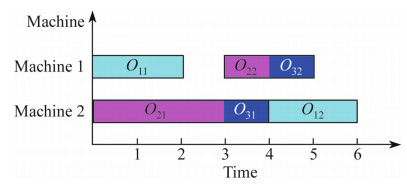
An example of 3 × 2 JSP is given in Table 1. The scheduling scheme can be well shown by Gantt chart. The Gantt chart for operation permutation (O11 → O21 → O22 → O31 → O32 → O12) is shown in Fig. 1. The horizontal axis represents processing time,as well as the longitudinal axis represents machine.
 |
|
Fig. 1 Gantt chart of ( |
GA has shown a good performance because of its global searching ability. However,the existing GAs for JSP usually have a slow convergence speed and are easy to fall into local optimal solutions. In order to improve the convergence speed and enhance search performance,we improve the basic GA for JSP. Figure 2 shows the flow chart of the AMGA. Firstly,n initial populations are generated randomly,suppose that the size of each population is M and each population evolves independently. Due to the randomness of genetic evolution,these n populations have different results in the evolutionary process,yet they will provide some help for judging good solution. In this paper,the co-evolution mechanism is adopted by combining lateral population collaboration with longitudinal population collaboration. Then in the evolutionary process of the lateral population collaboration,the same number of the best individuals from each population by employing selection,adaptive crossover (the adaptive crossover probability is pc,as shown in Fig. 2) and adaptive mutation operators (the adaptive mutation probability is pm) are selected averagely to form M individuals and saved in the population p0. Meanwhile,in the evolutionary process of the longitudinal population collaboration,M best individuals based on the calculated fitness values are chosen to form a new population (n + 1) from all populations. The individuals with much higher fitness would replace the smaller individuals with lower fitness in population p0.
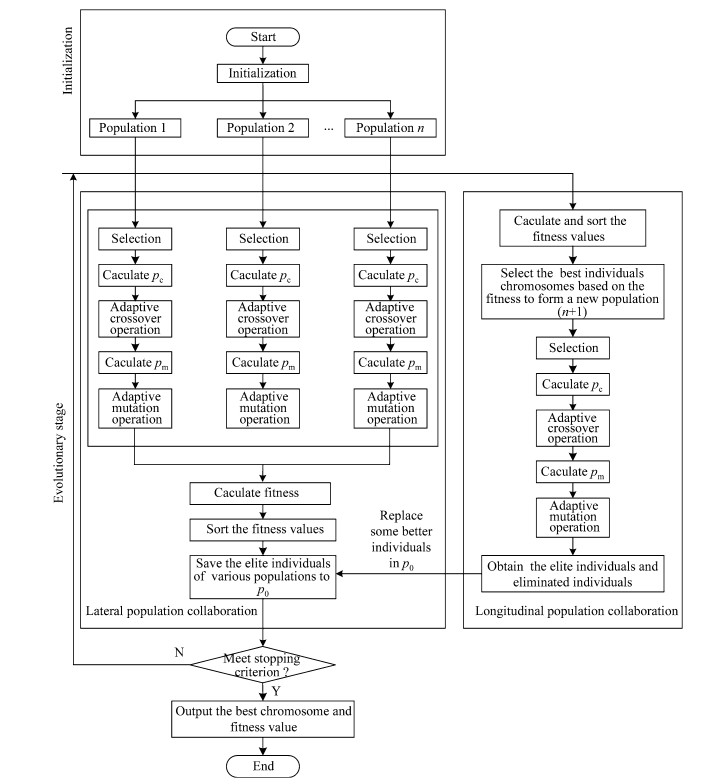 |
| Fig. 2 Flow chart of the AMGA |
A chromosome has gene information for dealing with JSP in GA. In this paper,we employ the operation-based encoding method for JSP because this encoding method is not difficult to use. This encoding method can avoid creating an unfeasible scheduling solution at any time. The chromosome shows the machining order of all jobs. Suppose that the number of machines is m and the number of jobs is n,then the chromosome includes m × n genes. Each job will appear m times and it will depend on an order relation. Therefore,each chromosome represents a feasible scheduling solution.
An example JSP of 3 jobs and 3 machines is given to explain the operation-based encoding and decoding method,and their processing procedures and times are shown in Table 2. An example of a chromosome is shown in Fig. 3. This chromosome is shown by 9 genes,"1" represents job 1,"2" represents job 2,and "3" represents job 3,respectively. Each gene (operation) is scheduled ordinarily from left side. In other words,each gene is given priority,and the gene on left position has a higher priority than the right. The scheduled gene is positioned at the best feasible solution. A chromosome can be decoded into a schedule indirectly. From Fig. 3 and Table 2,the first gene "1" is the first operation of job 1,which is performed on machine 1 and the processing time is 2. The second gene "3" is the first operation of job 3,which is performed on machine 2 and the processing time is 1. The third gene "2" is the first operation of job 2,which is performed on machine 2 and the processing time is 3. The fourth gene "3" is the second operation of job 3,which is performed on machine 1 and the processing time is 1. The fifth gene "1" is the second operation of job 1,and so on. Therefore,the scheduling result is obtained (see Fig. 4).
 |
| Fig. 3 Chromosome |
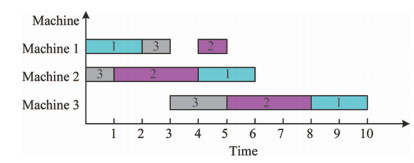 |
| Fig. 4 Scheduling result |
The purpose for defining fitness function is to evaluate the individual qualities,and it usually has a relationship with the objective function. The bigger the fitness value of a chromosome is,the bigger its probability for surviving in the population. In this study,we define the fitness function as g(x) = 1/g,where x is any individual in the population.
A suitable selection approach has an influence on GA performance by increasing the speed of obtaining optimal or near-optimal solution [23]. The roulette wheel selection method of which the selected probability of an individual is proportional to its fitness value,is adopted by most of GA selection strategies. Therefore,we also use this selection method in our work.
4.3 Crossover operatorThe mechanism of the order-based crossover is described as follows. Firstly,two crossover points are chosen from the gene strings randomly and equably. Then,the parts between the two cut points are passed to the two offsprings. Thirdly,the remaining left hand and right hand sides of each offspring are constructed by going over its second parent and eliminating the same numbers with the passed part of its first parent,and filling up the missing left and right sides according to an order existing on its second parent. Figure 5 shows an example for this operator.
 |
| Fig. 5 Crossover operator |
The traditional adaptive crossover probability and mutation probability are designed as follows [30]:
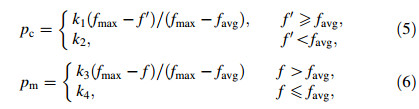
where k1,k2,k3,k4 ≤ 1:0; favg,fmax represent the average fitness and maximum fitness of the individuals of each generation,respectively; f' is the larger of the fitness values of the solutions to be crossed; f is the fitness of chromosome which is to be mutated.
This kind of adaptive GA has some disadvantages. In the early evolution,the good individual of population almost keeps unchangeable,however the good individual may not be the global optimal one at this time. As a result,this would increase the possibility of the local convergence. Therefore,in order to accelerate evolutional speed and enlarge searching scope,a novel adaptive crossover probability is proposed as follows.
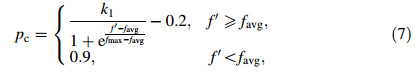
If the individual fitness value is higher than the population average fitness,then the crossover probability pc will become smaller in order to make better chromosome evolved into the next generation,and vice versa.
4.4 Mutation operatorThe mall perturbation on chromosomes is produced by mutation operator for maintaining the diversity of population. It is not difficult to make some mutation operators for permutation representation. Neighborhood search-based mutation operator is used in Ref. [7]. For permutation representation,the neighborhood for a given chromosome can be considered as a set of transformable chromosomes from a given chromosome by exchanging the positions of 3 genes (randomly selected and non-identical genes). The examples of mutation are given in Fig. 6.
 |
| Fig. 6 Mutation operator |
In our method,we select the best chromosome based on the calculated fitness to form a new offspring. In order to accelerate convergence speed and increase individual diversities,the novel adaptive mutation probability is proposed as follows.

The crossover and mutation probabilities can be regulated automatically according to the fitness. Meanwhile,the pc and pm with the largest individual fitness in population are not equal to zero. This adaptive method can avoid falling into an almost stagnant state,and therefore this algorithm can escape from local optimal solution to overcome the precocious shortcomings.
4.5 ReplacementThe offspring generation is formed by employing selection and genetic operators from the parent generation. The offspring generation replaces the parent generation only after the new population is created completely. We apply elitism to replace the relatively bad individuals of offspring population with good individuals of the population (n + 1).
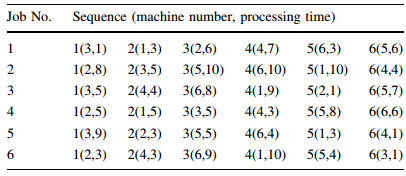
5 Experiment and analysis 5.1 Comparison for MT benchmark problemsThe performance of our proposed AMGA is evaluated by comparing with other approaches in MT problem,which is extremely often used as benchmark problem [31]. MT problem has three instances: MT06,MT10,and MT20. Among these,MT06,MT10 are of particular interest because almost all algorithms proposed for dealing with JSP have used them as benchmarks. We can obtain the optimal solutions for MT06 and MT10 benchmark problems,which are 55 and 930,respectively. The approach solution for MT20 problem is 1 165. Table 3 shows the machining information for MT06 benchmark problem.
We executed our algorithm in VC language and ran it on a PC with 4G main memory. The AMGA parameters are selected as follows: population size M is 100,population number 4,the maximum generation 50,k1 2.2,k2 0.5. The scheduling Gantt chart is shown in Fig. 7. The comparisons of convergence speed for MT06 benchmark problem are obtained (see Fig. 8) by GA and AMGA under the same evolutionary environment. The best value (55 time units) can be obtained by GA and AMGA. It needs only 5 generations by AMGA for finding the best value. Meanwhile,this simulation results are obtained from a random test. However,the best value which is selected from lots of tests needs 11 generations by traditional GA. The simulation result indicates that the convergence rate and stability of AMGA are remarkably better than those of the traditional GA.
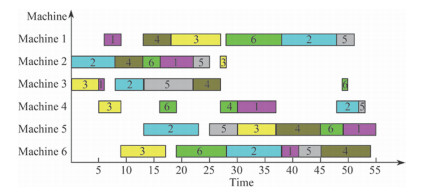 |
| Fig. 7 Gantt chart for MT06 benchmark problem |
 |
| Fig. 8 Comparisons of convergence speed for MT06 benchmark problem |
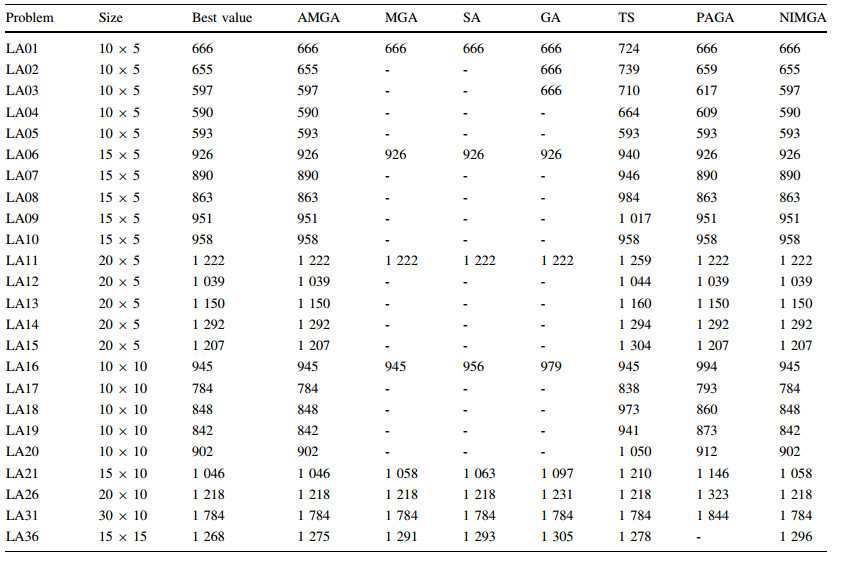
Table 4 summarizes the best results obtained by AMGA algorithm and previous approaches including GA [32],SA [33],tabu search (TS) [34],modified genetic algorithm (MGA) [8],parallel agent-based genetic algorithm (PAGA) [28],and new island model genetic algorithm (NIMGA) [27] for MT benchmark problems. From Table 4,it can be concluded that the basic GA,TS,SA and AMGA proposed in this paper can reach the best value of the problem for simple MT06 benchmark problem. However,GA,TS and PAGA can not get the best value for MT10 benchmark problem. Meanwhile,GA,TS,PAGA and NIMGA can not get the best value for more complicated MT20 benchmark problem for every test. The AMGA proposed in this paper can almost get the best value for every complicated scheduling problem. Figure 9 shows the details of the frequency distribution of solutions given by 100 trials. From Fig. 9,it can be seen that 52 trails (more than half of the total trails) can get the best value.
 |
| Fig. 9 Frequency distribution details of makespan for MT20 (20 × 5) |
AMGA is also used to solve some complicated typical scheduling LA benchmark problems [31],and the improved performance is observed in comparison with GA [32],SA [33],TS [34],MGA [8],PAGA [28] and NIMGA [27]. Table 5 shows the experimental results on LA benchmark problems. Figure 10 shows the details of the frequency distribution of solutions from 100 trials.
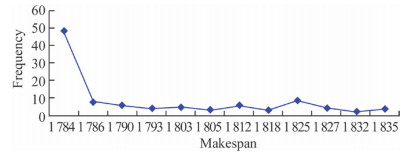 |
| Fig. 10 Frequency distribution details of makespan for LA31 (30 × 10) |
From Table 5 it can be concluded that GA,SA,PAGA,NIMGA and AMGA can reach the best value of the problem for simple LA benchmark problems,however the basic GA can not get the best value for every complicated scheduling problem for every test. The AMGA can almost get the best value for every complicated scheduling problem. From Fig. 10,it can be seen that nearly half of the 100 times can get the best value. The experimental results for complicated LA benchmark problems by AMGA are not worse,even better than those obtained by IMGA and NIMGA. Since these results were obtained in such situations,we firmly believe that IMGA is very effective. Though the makespan of the optimal solutions could not be obtained for every complicated problem,yet as an approximate solution method,we consider them to be sufficient results.
6 ConclusionsMany pre-proposed basic evolutionary algorithms for JSP usually have a slow convergence speed and are easy to trap into local optimal solutions. Therefore,an improved AMGA is proposed,and the four main aspects (multipopulation,adaptive crossover probability,adaptive mutation probability and the elite replacing mechanism) are proposed or used in AMGA to solve JSP. To evaluate the effectiveness of the proposed AMGA,a lot of benchmark problems have been tested and the comparisons among some other algorithms are also presented. Computational results show that the proposed AMGA is an effective method for dealing with the JSPs.
Acknowledgments This paper is supported by the National Natural ScienceFoundationofChina(GrantNo.51305001),KeySupportProjects for Outstanding YoungTalents of AnhuiProvince Universities(Grant No. gxyqZD2016125),and Anhui Key Laboratory Open Project of Advanced Numerical Control and Servo Technology (Grant No. xjsk003).| 1. | Pezzella F, Morganti G, Ciaschetti G (2008) A genetic algorithm for the flexible job-shop scheduling problem.Comput Oper Res 35(10):3202-3212 |
| 2. | Gao L, Li X, Wen X et al (2015) A hybrid algorithm based on a new neighborhood structure evaluation method for job shop scheduling problem.Comput Ind Eng 88:417-429 |
| 3. | Nasser SP, Behrooz G (2013) A novel hybrid meta-heuristic algorithm for solving multi objective flexible job shop scheduling.J Manuf Syst 32(4):771-780 |
| 4. | Garey MR, Johnson DS, Sethi R (1976) The complexity of flow shop and job shop scheduling.Math Oper Res 1(2):117-129 |
| 5. | Lin TL, Horng SJ, Kao TW et al (2010) An efficient job-shop scheduling algorithm based on particle swarm optimization.Expert Syst Appl 37(3):2629-2636 |
| 6. | Goncalves JF, Mendes JJDM, Resende MGC (2005) A hybrid genetic algorithm for the job shop scheduling problem.Eur J Oper Res 167(1):77-95 |
| 7. | Park BJ, Choi HR, Kim HS (2003) A hybrid genetic algorithm for the job shop scheduling problems.Comput Ind Eng 45(4):597-613 |
| 8. | Wang L, Zheng DZ (2001) An effective hybrid optimization strategy for job shop scheduling problems.Comput Oper Res 28(6):585-596 |
| 9. | Watanabe M, Ida K, Gen M (2005) A genetic algorithm with modified crossover operator and search area adaptation for the job-shop scheduling problem.Comput Ind Eng 48(4):743-752 |
| 10. | Nowicki E, Smutnicki C (2005) An advanced tabu search algorithm for the job shop problem.J Sched 8(2):145-159 |
| 11. | Ponnambalam SG, Aravindan P, Rajesh SV (2000) A tabu search algorithm for job shop scheduling.Int J Adv Manuf Technol 16(10):765-771 |
| 12. | Ge HW, Sun L, Liang YC et al (2008) An effective PSO and AISbased hybrid intelligent algorithm for job-shop scheduling.IEEE Trans Syst Man Cybern (Part A) 38(2):358-368 |
| 13. | Udomsakdigool A, Kachitvichyanukul V (2008) Multiple colony ant algorithm for job-shop scheduling problem.Int J Prod Res 46(15):4155-4175 |
| 14. | Suresh RK, Mohanasundaram KM (2005) Pareto archived simulated annealing for job shop scheduling with multiple objectives.Int J Adv Manuf Technol 29(1):184-196 |
| 15. | Li Y, Chen YA (2010) Genetic algorithm for job shop scheduling. J Softw 5(3):269-274 |
| 16. | Mattfeld DC, Bierwirth C (2004) An efficient genetic algorithm for job shop scheduling with tardiness objectives.Eur J Oper Res 155(3):616-630 |
| 17. | Gao L, Zhang GH, Zhang LP et al (2011) An efficient memetic algorithm for solving the job shop scheduling problem.Comput Ind Eng 60(4):699-705 |
| 18. | Liu TK, Tsai T, Chou JH (2006) Improved genetic algorithm for the job-shop scheduling problem.Int J Adv Manuf Technol 27(9):1021-1029 |
| 19. | Ahmadizar F, Farahani MH (2012) A novel hybrid genetic algorithm for the open shop scheduling problem.Int J Adv Manuf Technol 62(5):775-787 |
| 20. | Wang L, Zheng DZ (2002) A modified genetic algorithm for job shop scheduling.Int J Adv Manuf Technol 20(1):72-76 |
| 21. | Zhang CY, Li G, Rao YQ et al (2005) A new hybrid GA/SA algorithm for the job shop scheduling problem.Lect Notes Comput Sci 3448:246-259 |
| 22. | Zhang CY, Rao YQ, Li PG (2008) An effective hybrid genetic algorithm for the job shop scheduling problem.Int J Adv Manuf Technol 39(9-10):965-974 |
| 23. | Yusof R, Khalid M, Hui GT et al (2011) Solving job shop scheduling problem using a hybrid parallel micro genetic algorithm.Appl Soft Comput 11(8):5782-5792 |
| 24. | Ren Q, Wang Y (2012) A new hybrid genetic algorithm for job shop scheduling problem.Comput Oper Res 39(10):2291-2299 |
| 25. | Lei DM, Guo XP (2015) An effective neighborhood search for scheduling in dual-resource constrained interval job shop with environmental objective.Int J Prod Econ 159:296-303 |
| 26. | Kurdi M (2015) A new hybrid island model genetic algorithm for job shop scheduling problem.Comput Ind Eng 88:273-283 |
| 27. | Kurdi M (2016) An effective new island model genetic algorithm for job shop scheduling problem.Comput Oper Res 67:132-142 |
| 28. | Asadzadeh L, Zamanifar K (2010) An agent-based parallel approach for the job shop scheduling problem with genetic algorithms.Math Comput Modell 52(11-12):1957-1965 |
| 29. | Gen M, Cheng R (1997) Genetic algorithms and engineering design.Wiley, New York |
| 30. | Srinivas M, Patnaik LM (1994) Adaptive probabilities of crossover and mutation in genetic algorithms.IEEE Trans Syst Man Cybern 24(4):656-667 |
| 31. | Muth JF, Thompson GL (1963) Industrial scheduling.Englewood Cliffs, New Jersey |
| 32. | Croce FD, Tadei R, Volta G (1995) A genetic algorithm for the job shop problem.Comput Oper Res 22(1):15-24 |
| 33. | Van PJM, Aarts EHL, Lenstra JK (1992) Job shop scheduling by simulated annealing.Oper Res 40(1):113-125 |
 2016, Vol. 4
2016, Vol. 4