The article information
- Xi-Kun Chen, Dong Sun
- Modeling and state of charge estimation of lithium-ion battery
- Advances in Manufacturing, 2015, 3(3): 202-211
- http://dx.doi.org/10.1007/s40436-015-0116-3
-
Article history
- Received: 2014-06-23
- Accepted: 2015-07-01
- Published online: 2015-07-29
With the rapidly growing demand on energy storage device (ESD),lithium-ion (Li-ion) battery is widely employed in smart grid and electric vehicles (EVs) and has been attracting a significant lot of attention. Compared to other batteries,Li-ion battery has been considered as the most promising power source due to the characteristics of highe Rp ower energy densities,smaller size,lower self-discharge and longer cycling life. However,battery pack management system (BMS) that interfaces with Li-ion batteries, coupled with the specific issues on safety and reliability operation,imposes such limitations on its application in ESD [1]. Hence,for further improvement on safety and performance maximization of the overall Li-ion batteries operating in ESD,plenty of researches have been carried out recently and much more techniques suited to BMS have been reported publicly [2, 3, 4, 5, 6, 7]. Among these techniques in the application fields,monitoring and prognostic techniques,accurate estimation of Li-ion battery internal states and efficient battery modeling are vital to improving the performance of ESD and extending its service life as long as possible. In this paper we focus on the Li-ion battery modeling for ESD and model parameter identification method,then based on the established model,estimate state of charge (SOC) of Li-ion battery using nonlinear filtering algorithm [7].
The most commonly used Li-ion battery models in ESD are categorized as electrochemical model and equivalent circuit model (ECM). Furthermore,a few models are combined with the techniques both in chemistry-based and circuit-based modeling [7].
Electrochemical modeling method adopts a number of partial differential equations to capture electrochemical physics and dynamic process inside Li-ion battery,which can employ different level approximations to simplify these equations and solutions to acquire different level fidelity battery models [8, 9, 10]. Although these models have a comprehensive structure comparison to other Li-ion battery models,they have been provided with desired fidelity and goals of outstanding modeling performance. Hence,there is a crucial trade-off that one must consider when choosing an applicable model for Li-ion battery in ESD. Universally,the more complex model used,the higher fidelity one can get,but the more computationally expensive it is [11]. Especially in real-time control system, higher fidelity model is usually not required at all. Thus, the computationally complex chemistry-based model is often used in laboratory so as to verify a newer battery performance,EVs cycle simulation,other intensive computation simulations,and so on [7].
ECM generally employs some resistors,capacitors and a controlled voltage source to form a circuit network that describes Li-ion battery transient response with the aim to approximate electrochemical physics and dynamics inside battery [12]. This modeling method takes advantage of the fairly simple structure of equivalent circuit network for real-time applications and facilitating internal states estimation of Li-ion battery. The circuit-based model with the simplification state-space equations is conveniently fused with different types techniques such as extended Kalman filter (EKF),state observer and least square (LS) identification method,and these methods are essentialy targeted to achieve accurate states estimation [12, 13, 14, 15, 16]. Hence,it is an important requirement for online states estimation being capable of running in real-time control system of ESD,and ECM is able to operate more efficiently than electrochemical model when implementing in embedded computer system [12].
Model parameter identification is a necessary procedure in battery modeling process and model fidelity mainly depends on model parameter identification method and accuracy of identified parameters. Generally,model parameters can be identified from experimental measurements in two ways,offline and online,corresponding to offline model and online one [17]. If ECM is the choice for Li-ion battery,offline model is often viewd as a look-up table in real-time control system,where these circuit element parameters have been obtained from battery tests offline. Furthermore,these parameters are usually variable depending on the environmental factors and battery operating conditions,such as ambient temperature,depth of discharge,discharge current rate,and battery aging. However,for online ECM,these parameters are often acquired in real time using identification method and always time-varying with actual factors and conditions. Least square (LS) parameter identification method is one of the most popular algorithms both applied to online and offline model parameters identification [17]. Hence,with the aim to accommodate the changing factors and conditions,an adaptive parameter identification method based on a variable forgetting factor least square (VFFLS) algorithm is introduced in this paper,and its recursive form (VFFRLS) for online modeling of Li-ion battery is also presented [18].
SOC is an important internal state of Li-ion battery and gives user an indication about energy remaining in battery and how much it will last before recharging. Thus accurate SOC estimation is vital to battery operating normally and will influence on battery health and safety in its overall service life [19].
Typically,SOC can be estimated using Coulomb counting method when the charge/discharge current through battery is measured,but current measurements are often polluted by measured noise derived from sensor detection errors. Hence long-time integral operation often results in a current drift. Although this method is simple and easy to implement in real-time control system,it is generally viewed as an open-loop method that needs calibration frequently. In addition,the open circuit voltage (OCV) when reaching the equilibrium battery voltage is of a relatively steady relation to SOC,which can be used to determine SOC directly. However,equilibrium OCV must be measured after a long resting time,and OCV-SOC relation curve naturally has such a plateau phase that it is difficult to estimate SOC precisely due to the voltage detection errors [20]. EKF technique known as a nonlinear filtering algorithm is commonly used to estimate SOC. This method combined with Coulomb counting method and OCV is achieving the closed-loop SOC estimation,where the feedback results from the deviation between modeled voltage values and battery measured values,therefore it has better robustness than single Coulomb counting method [21, 22, 23]. Another nonlinear filter named unscented Kalman filter (UKF) is also employed to predict battery SOC. This technique,choosing a set of sigma points and weights to match nonlinear function,mainly depends on numerical approximations rather than analytic approximations of EKF using the first-order Taylor-series expansion [24, 25]. Although UKF has a more accuracy estimation than EKF, while the model dimension increases,these weights may be negative and the matrix in computational procedure may probably be non-positive definite,which is likely to result in state estimation divergence [26]. Hence,for a solution to the numerical stability issue,an alternative nonlinear Kalman filter technique known as cubature Kalman filter (CKF) is introduced in this paper [27].
The remainder of this paper is structured as follows. Section2describes RC equivalent circuit model of Li-ion battery. The variable forgetting factor recursive least square identification method is introduced in Sect.3. Section4shows CKF technique and Li-ion battery SOC estimation. Section5summarizes the main conclusions. 2 Li-ion battery model 2.1 Equivalent circuit model
Commonly used ECMs include Rint model,Thevenin model,the partnership for a new generation of vehicles (PNGV) model,the National Renewable Energy Laboratory (NREL) model,Randles model and RC model. Although these ECMs vary in complexity and fidelity,they are finally equivalent to each other in certain extent [12].
As shown in Fig. 1,RC ECM is often used to model Liion battery,and it is usually composed of a series of resistor-capacitor pair circuit from Rp,1 ,Cp,1 to Rp,n ,Cp,n and a serial ohmic resistance Ro. Uo represents the voltage drop due to ohmic polarization.Uoc is OCV,and Up,1 to Up,n denote the transient voltages arising from activation polarization and concentration polarization [12]. UL1 is the battery terminal voltage. The number n of series RC pairs represents the ECM order. Higher order circuit-based model describes more voltage dynamics,obviously more model fidelity leads to more computation complexity. Thus the first-order and second-order RC ECMs are always the balanced choices.
 |
| Fig. 1 RC equivalent circuit model |
As shown in Fig. 2,NREL model is another ECM developed in the National Renewable Energy Laboratory [13]. Although it has a different circuit structure from Rc ECM,when setting the resistor Rc to zero and after stardelta transformation fromRo ,Rb ,Cc to Ro ,Rp ,Cp,itis becoming the first-order RC ECM. Thus NREL ECM is fundamentally equal to RC ECM.
 |
| Fig. 2 NREL equivalent circuit model |
Randles ECM shown in Fig. 3 is derived from electrochemical impedance spectroscopy (EIS) and its circuit parameters are from EIS measurements [14]. Furthermore, its circuit elements of ZW are also equivalent to RC pair circuit through circuit approximation and simplification [15]. To sum up,these ECMs have similar features in circuit principle and then we choose the first-order RC ECM as an example in this paper.
 |
| Fig. 3 Randles equivalent circuit model |
According to basic circuit theorem,the transfer function of the first-order RC ECM shown in Fig. 1 is derived as

Because of the samples data of input current and output voltage of Li-ion battery,G(s) needs to be discretized. The discretization methods widely used include forward/backward Euler transformation,bilinear transformation and impulse invariant transformation. Hence the discrete-time system G(z) and the corresponding difference equation are shown as


An auto-regressive with exogenous input (ARX) model is visually derived from Eq. (3),where ek is a stochastic white noise with zero mean and normal distribution. The universal form of ARX model is shown as

Then we make the conclusions,if the sampling interval time Ts is small enough,the discretization procedure can guarantee the discrete-time system stabilization and ARX model will be suited for real-time applications. Furthermore,different ECMs can be transformed into the same form ARX model at last,and its parameters will be identified in the next step. The difference is that the parameters are derived from different calculation formulas. Hence,this model is a better choice for Li-ion battery,and when any circuit parameter is needed,we can choose the corresponding calculation formula from Table 1. 2.3 Discrete state-space model 2.3.1 Equivalent circuit state-space model As shown in Fig. 1,when giving the first-order RC ECM a charge currenti,UL is


Thus a discrete-time state-space model can be defined as:

If ARX model was selected,we would have derived a similar discrete-time state-space model. Based on the difference equation from Table 1,define the transient voltage Ut,k=Uk,then the equation shown as

Hence a discrete-time state-space model will be defined as follows

ARX model is theoretically rational and actually suitable for Li-ion battery for the following reasons:
(i) For a discrete-time system,ARX model is suited for Li-ion battery,because BMS substantially has the characteristics of discrete-time system. Supposing that the sampling interval time Ts is small enough,any sampling data of voltage,current and working temperature measured by sensors are able to express the dynamics of Li-ion battery.
(ii) Most ECMs are basically equivalent to each other and required to be transformed from continuoustime system to discrete-time system. Finally we would obtain the similar ARX model as well.
(iii) For online modeling,ARX model shown as Eq. (9) has some undetermined coefficients that can be acquired in real-time applications by online parameter identification method.
(iv) The discrete-time state-space model,shown as Eq. (10),is derived from ARX model,and its undetermined coefficients are from the identified parameters. Hence it is suitable for estimating the states of Li-ion battery online.
(v) It is able to achieve online modeling and online states estimation of Li-ion battery based on the developed ARX model,which can alleviate the complexity of offline model,and it has a more flexible structure and a simpler transformation process than ECM. The detailed analysis is shown in Ref. [19]. 3 Model parameter identification 3.1 Parameter identification method
Due to the varying environmental factors and changing operation conditions of Li-ion battery,the real-time BMS needs to be operated based on the parameter-varying lineaRmodel. However,it tends to be difficult that these parameters are variable with actual conditions and require calibration in time. Generally,RLS and FFRLS algorithms are used for online modeling. Once significant changes occur in load or environment conditions,these methods cannot adapt to the real factors well. Therefore,the variable forgetting factor was appended to amend FFRLS algorithm, and it will be shown in this section [18].
According to the least square principle,the general model is shown as

Hence,based on ARX (1,1) model,the computational procedure of VFFRLS algorithm is shown as follows.
Step 1 Initialization

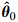 is the parameters matrix and the initial values
are always set small enough;P0 is the initial covariance
matrix and I is the identity matrix.
is the parameters matrix and the initial values
are always set small enough;P0 is the initial covariance
matrix and I is the identity matrix.
Step 2 Collect the input current and the output voltage, update the information vector

Step 3 Predict the output voltage

Step 4 Update the estimation error

Step 5 Update the variable forgetting factor

Step 6 Calculate the recursive gain matrix Kk

Step 7 Estimate the parameters


HPPC test results are from Freedom CAR Battery Test Manual [19]. According to the test measurements,we can obtain available model parameters.
Hence,a LiFePO4cell with the nominal voltage of 3.2 V and the rated capacity of 20 A·h has been tested. For as much of the 10%-90% SOC region as possible,the cell has been charged to 100% SOC with the high limit voltage of 3.65 V and the cutoff current 0.5 A,then it was discharged under different discharge current rates of 1C,2C and 2.5C until the low limit voltage 2 V is reached. In order to keep the cell under an isothermal condition,a thermal chamber was equipped for the cell that kept the variation of working temperature of the cell surface within ±2 ℃. A host computer is used to record the cell operating status,such as discharge current with measurement precision of±10 mA, terminal voltage with the precision of ±1 mV,working temperature with the precision of ±0.5℃ and depth of discharge (DOD),which were measured via BMS. The designed test profiles at 1C discharge current rate are shown in Fig. 4,where SOC reference value was calculated by BMS in real time,and other tests under the different discharge current rates have the similar profiles.
 |
| Fig. 4 Designed test profile at 1C discharge current rate |
To validate the performance of VFFRLS identification algorithm and designed ARX model,these identified parameters were transformed from coefficient values to electrical element values of the first-order RC ECM.
Figure 5 shows the identified circuit parameters at 1C discharge current rate with different SOCs. It is the same trend that these parameters increase slowly as SOC gradually decreases in the 90%-30% SOC region,but they become to increase quickly in the 30%-0% SOC region. The fitting curves describe the trend in Fig. 5. Hence,it can be seen that such SOC dependency of the parameters is not obvious when the cell operates in the normal DOD region.
 |
| Fig. 5 Identified parameters at 1C discharge current rate |
Under different discharge current rates and SOCs,the three-dimensional stereograms of the identified parameters are shown in Fig. 6. Due to the limitation of maximum discharge current rate 2C of the cell,the presented current rate is within 1C-2.5C and the middle current values were obtained using piecewise interpolation technique. Moreover,more serious polarization effect results in more energy loss,consequently higher resistance,when the discharge current is closer to the limit rate.
 |
| Fig. 6 Identified parameters under different discharge current rates and SOCs |
Containing important information that can help to estimate Li-ion battery SOC,OCV is widely used for modeling battery properties. OCV-SOC regarded as a nonlinear function,is commonly implemented in embedded computer as a look-up table,and the mapping curve is always linearized to approximate its nonlinear characteristics [20].
For the fidelity mapping curve,experiments have been carried out under a room temperature and the cell was discharged under initial SOC 100% for 5 min with a long rest time interval of more than 1 h,which can ensure OCV back to the equilibrium voltage. Consequently,the experimental data are shown in Fig. 7.
 |
| Fig. 7 Identified OCV-SOC mapping curve |
Conventionally,to obtain the OCV-SOC function,the mapping curve needs to be fitted using the high-ordeRpolynomial curve,even higher than the fifth-order,for forming a look-up table in embedded computer. Figure 7 shows a sixth-order polynomial fitting curve. However,this approach would lead to more computational errors and a lower computational efficiency because of the limitation of word length in embedded computer,as well as causing over-fitting issue. In addition,the mapping curve has a flat region known as plateau phase,and the state observability would be affected. Thus it is the disadvantage that more SOC estimation errors would occur,unless keeping the monotonicity of the mapping curve. Hence,a piecewise cubic Hermite interpolation technique was used for the mapping curve with no more than the third-order polynomial fitting,and it is beneficial to observable states and real-time application,as shown in Fig. 7. 3.5 Model verification
For the reliability verification of the designed model,the first-order RC circuit model has been subsequently simulating in MATLAB software with the identified circuit parameters. In comparison to the experimental measurements,the results show that the maximum error is within 5% and the root mean square error (RMSE) is about 2%. 4 SOC estimation of Li-ion battery 4.1 CKF
CKF is a new nonlinear filter for high dimensional state estimation and the core of CKF is a third-degree sphericalradial cubature rule [27].
Considering an n-dimensional nonlinear stochastic system and through the rigorous numerical derivation,the CKF generates 2n cubature points and all the points lie inside the region of integration,which makes these cubature weights positive. In comparison,UKF entails 2n+1 sigma points,while the system dimension exceeds three,the sigma point weights may be negative. Although both filters can be equally exact at least up to a fourthdegree polynomial and have equivalent estimation accuracy,the CKF has better numerical stability than UKF [27]. 4.2 CKF algorithm
A standard state-space model of discrete-time nonlinear stochastic system is shown as

The algorithm computational procedure mainly includes two steps,time update and measurement update,which are shown as follows.
Step 1 Initialization

Step 2 Time update. Choose 2n cubature points and evaluate the propagated cubature points Xk :

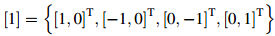 When
n=2,ξi
are the point weights and chol(·) is a Cholesky
factorization function to calculate the square roots of
covariance matrix.
Step 3 Time update. Estimate the predicted state
When
n=2,ξi
are the point weights and chol(·) is a Cholesky
factorization function to calculate the square roots of
covariance matrix.
Step 3 Time update. Estimate the predicted state 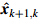 and the predicted error covariance Pkþ1;k
and the predicted error covariance Pkþ1;k

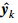



Accurate SOC estimation for Li-ion battery in BMS is a case challenge,because electrochemical battery dynamic behavior has obviously nonlinear characteristics due to the variable environmental factors and its operating conditions. Although the time-varying parameters linear model is widely used for the approximation of dynamic properties of Li-ion battery,there is still the low-degree nonlinearity in the real system that would result in inaccurate prognostication of battery internal states,so nonlinear filters such as EKF and UKF are generally used to estimate battery internal state.
According to CKF algorithm,we can verify the SOC estimator based on the designed model through substituting Eq. (20) by Eq. (8)orEq.(10). To better evaluate the performance of SOC estimator in a relatively realistic automotive environment,urban dynamometer drive schedule (UDDS) test was conducted in 2 cycles with 2740 s duration time and 1 Hz sampling rate which were derived from advanced vehicle simulator developed in NREL. The BMS has recorded the battery operating data with initial SOC of 90%,such as current values,voltage values, working temperature and reference SOC values,which were calculated by BMS online based on the Coulomb counting method. Then a comparative study between both the SOC estimators based on EFK and CKF was carried out and the contrastive results are shown in Fig. 8.
 |
| Fig. 8 SOC estimation contrastive curves of UDDS test |
The UDDS test is shown in Fig. 8a,which gives the velocity of electric vehicle. From Fig. 8b,it can be seen that the maximum estimation error is about 5% when using the SOC estimator based on EKF algorithm. However,the maximum estimation error is within 2.3% when using CKF estimator,as shown in Fig. 8c. Figure 8d presents the SOC estimation errors of different estimators. For further validation of the performance difference of both estimators, Table 2 shows the RMSEs of different algorithms in SOC estimation.
To summarize,EKF relies mostly on such analytic approximations of system states by the first-order Taylorseries expansion that it can only reach equivalent first-order estimation precision. CKF is comparatively more accurate than EKF algorithm,which can achieve the third-order estimation precision at least,because it mainly depends on numerical approximations. Meanwhile,CKF is able to acquire more numerical stability than UKF. Hence,using CKF nonlinear filtering technique can improve the performance of SOC estimation by up to 50% than using EKF algorithm. 5 Conclusions
This paper presents the widely used modeling method for Li-ion battery,and shows the characteristics of circuitbased model and chemistry-based one. The circuit-based models are essentially equivalent to each other through circuit transformation,approximation and simplification. For the trade-off on model fidelity and computational complexity,the first-order RC ECM is selected for Li-ion battery,and then it results in an ARX model. For the discrete-time characteristics of BMS and the simplification of parameterization process,ARX model is a better choice for Li-ion battery.
Based on the designed model,the recursive least square algorithm with a variable forgetting factor,known as an adaptive parameter identification method for the timevarying system,is then used for battery model parameters identification. To validate the method reliability and the model fidelity,HPPC tests were implemented for a LiFePO4 cell with the nominal voltage of 3.2 V and the rated capacity of 20 A·h under different discharge current rates and different SOCs. Consequently,the model parameters have been identified from the test measurements. This paper also shows the corresponding circuit element parameters.
OCV-SOC mapping curve is an important element in Liion battery model,but the traditional fitting curve using high-order polynomial fitting would lead to large computational error,low computational efficiency,over-fitting issue,etc. Thus the piecewise cubic Hermite interpolation method,as a solution to these problems,is applied to fit the OCV-SOC mapping curve and guarantee the reliability of this mapping curve.
In order to improve the performance of SOC estimator,a nonlinear Kalman filter technique named cubature Kalman filter is presented in this paper. In comparison with EFK and UKF techniques,CKF algorithm has more numerical stability than UKF and more accuracy estimation than EKF. In UDDS test,the experimental results show that the maximum estimation error is only about 2.3%,and the SOC estimation performance have been improved by up to 50%.
Acknowledgments Project supported by the National High Technology Research and Development of China 863 Program (Grant No. 2011AA11A247).| 1. | Habiballah RE, Unnati O (2013) Battery management system: an overview of its application in the smart grid and electric vehicles. IEEE Ind Electron Mag 6:4-16 |
| 2. | Zhang JL, Lee J (2011) A review on prognostics and health monitoring of Li-ion battery. J Power Sources 196:6014-6077 |
| 3. | Barre A, Deguilhem B, Grolleau S et al (2013) A review on lithium-ion battery aging mechanisms and estimations for automotive applications. J Power Sources 241:680-689 |
| 4. | Lu LG, Han XB, Li JQ et al (2013) A review on the key issue for lithium-ion battery management in electric vehicle. J Power Sources 226:272-282 |
| 5. | Waag W, Fleischer C, Sauer DU (2014) Critical review of the method of lithium-ion batteries in electric and hybrid vehicles. J Power Sources 258:321-339 |
| 6. | Rezvanizaniani SM, Liu ZC, Chen Y et al (2014) Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (EV) safety and mobility. J Power Sources 256:110-124 |
| 7. | Seaman A, Dao TS, Mcphee J (2014) A survey of mathematicsbased equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J Power Sources 256:410-423 |
| 8. | Schmidt AP, Bitzer M, Imre AW et al (2010) Experiment-driven electrochemical modeling and systematic parameterization for a lithium-ion battery cell. J Power Sources 195:5071-5080 |
| 9. | Moura SJ, Chaturvedi NA, Krstic M (2012) PDE estimation techniques for advanced battery management systems—part 1: SOC estimation. In: American control conference, Montréal, Canada, pp 559-565 |
| 10. | Moura SJ, Chaturvedi NA, Krstic M (2012) PDE estimation techniques for advanced battery management systems—part 2: SOH identification. In: American control conference, Montréal, Canada, pp 566-571 |
| 11. | Marcicki J, Canova M, Conlisk AT et al (2013) Design and parameterization analysis of a reduced-order electrochemical model of graphite/LiFePO4 cells for SOC/SOH estimation. J Power Sources 237:310-324 |
| 12. | Hu X, Li S, Peng H (2012) A comparative study of equivalent circuit models for Li-ion batteries. J Power Sources 198:359-367 |
| 13. | Sitterly M, Wang LY, Yin GG et al (2011) Enhanced identification of battery models for real-time battery management. IEEE Trans Sustain Energy 2(3):300-308 |
| 14. | Andre D, Meiler M, Steiner K et al (2011) Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. 1. Experimental investigation. J Power Sources 196:5334-5341 |
| 15. | Andre D, Meiler M, Steiner K et al (2011) Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. 2. Modelling. J Power Sources 196:5349-5356 |
| 16. | Hu Y, Yurkovich S, Guezennec Y et al (2009) A technique for dynamic battery model identification in automotive applications using linear parameter varying structures. Control Eng Pract 17(10):1190-1201 |
| 17. | Li Y, Wang LF, Liao CL et al (2014) Rescursive modeling and online identification of lithium-ion batteries for electric vehicle application. Sci China Technol Sci 57(2):403-413 |
| 18. | Constantin P, Jacob B, Silviu C (2008) A robust variable forgetting factor recursive least-squares algorithm for system identification. IEEE Signal Proc Lett 15:597-600 |
| 19. | Yuan SF, Wu HJ, Yin CL (2013) State of charge estimation using the extended Kalman filter for battery management systems based on the ARX battery model. Energies 6:444-470 |
| 20. | Weng CH, Sun J, Peng H (2014) A unified open-circuit-voltage model of lithium-ion batteries for state-of-charge and state-ofhealth monitoring. J Power Sources 258:228-237 |
| 21. | Plett GL (2004) Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 1: background. J Power Sources 134:252-261 |
| 22. | Plett GL (2004) Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 2: modeling and identification. J Power Sources 134:262-276 |
| 23. | Plett GL (2004) Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 3: parameter estimation. J Power Sources 134:277-292 |
| 24. | Plett GL (2006) Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs. Part 1: introduction and state estimation. J Power Sources 161: 1356-1368 |
| 25. | Plett GL (2006) Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs. Part 2: simultaneous state and parameter estimation. J Power Sources 161:1369-1384 |
| 26. | Li JH, Barillas JK, Guenther C et al (2013) A comparative study of state of charge estimation algorithm for LiFePO4 batteries used in electric vehicles. J Power Sources 230:244-250 |
| 27. | Arasaratnam I, Haykin S (2009) Cubature Kalman filters. IEEE Trans Autom Control 54(6):1254-1269" |
 2015, Vol. 3
2015, Vol. 3