The article information
- Liu-Ming Yan, Jun-Ming Su, Chao Sun, Bao-Hua Yue
- Review of the first principles calculations and the design of cathode materials for Li-ion batteries
- Advances in Manufacturing, 2014, 2(4): 358–368
- http://dx.doi.org/10.1007/s40436-014-0086-x
-
Article history
- Received: 2014-03-16
- Accepted: 2014-06-27
- Published online: 2014-07-19
2. Department of Physics, College of Sciences, Shanghai University, Shanghai, People’s Republic of China
The rapid industrialization and urbanization of modern China benefit greatly from the over exploitation of fossil fuels and other nature resources. However, such development is reaching the critical point of resources supply and environmental tolerance. In 2012, China consumed 2.8 billion tons of coal (about half of the overall world consumption), and 490 million tons of petroleum. Now, China is the second largest petroleum importer, and will become the largest importer in the near future. Even to pursue moderate economy growth, China has to maintain about 4 % yearly growth in energy supply. Therefore, it is important to develop advanced energy technologies for the exploitation of renewable energies, such as wind power and solar energy, and for the efficient and environmentally friendly use of fossil fuels.
In our times, the scientific and industrial communities have identified several advanced energy technologies, such as batteries and super capacitors, fuel cells, solar cells, and thermochromic coatings, as competitive candidate technologies for our society. However, the large scale commercializations of these advanced energy technologies depend on the development of several advanced energy materials. For example, the application of Li-ion batteries in electric vehicles depends on the development of anode and cathode materials, proton exchange membrane fuel cells on the proton exchange membranes and the electrocatalysts, thermochromic coatings on the thermochromic materials. And the lack of adequate and affordable advanced energy materials has hindered our society to overcome energy and environmental crises. In this paper, we present an overview of the computation approach for the development of cathode materials for Li-ion batteries, with an emphasis on the first principles calculations and the rational design of these materials.
The advanced cathode materials for Li-ion batteries are developed in three phases, requirement specification, screening for candidate compound, and developing the candidate compound into a commercial material. The requirement specification is identified by the domain experts according to the specific application, and it is the target of the advanced cathode materials for Li-ion batteries. The next two phases are carried out by materials scientists and engineers. In order to develop advanced cathode materials for Li-ion batteries, researchers have to firstly identify candidate compound by screening databases of existing compounds and/or by virtual screening of possible compounds which have not been synthesized or identified, and then to engineer the candidate compound via modification for commercial applications. For example, Padhi et al. [1] identified the olivine lithium iron phosphate as competitive cathode material for Li-ion batteries because of its relatively high energy density, low cost, and safety concerns compared to LiCoO2. However, the thermodynamic properties only provide this material the possibility as cathode material for Li-ion batteries and its commercial application is a result of years of efforts on the improvement of this material [2]. The process of commercialization of a material is slow and costly. As a matter of fact, Eagar showed that the average time required for new materials to be commercialized was 20 years [3].
In order to accelerate the commercialization process of novel materials, the full use of experimental and theoretical information ever accumulated in literatures and databases is critically important. Recently, a Materials Genome Project (MGP) was launched at MIT aiming to perform large-scale property computations on all known inorganic compounds and to make that basic information available for materials research discovery [4]. In Shanghai University, the 085 Knowledge Innovation Program is being carried out for the development of novel materials, especially of the materials applied in extreme environments.
In the following sections, we are going to overview the first principles calculations and design of cathode materials for Li-ion batteries including the calculation of energies, structures, and band-gap energies, phase diagram calculations, kinetic mechanism of Li-ion transport, and data mining and high-throughput ab initio calculations. We will also overview the first principles investigation of sodium ion intercalation materials for the emerging technology of sodium ion batteries. Finally, we will summarize the most important achievements and preview the challenges and opportunities of this rapidly developing field. 2 Calculations of energies and structures
In the field of solid state inorganic materials, density functional theory (DFT) is among the most popular and versatile methods to calculate their energies and structures. Several levels of approximations, including the local density approximation (LDA), the generalized gradient approximation (GGA), and the so called GGA + U method, are widely accepted for such calculations. The functionals PW91 and PBE and hybrid functionals PBE0 and HSE06 are popular for solid state calculations [5]. The difference between PBE and PBE0 functional is that a quarter of PBE exchange is substituted by the exact Hartree-Fock exchange [6, 7]. The functional HSE03 and HSE06 were developed to overcome the expansive Hartree-Fock calculations, in which only short range interaction was described using Hartree-Fock exchange [8, 9]. The calculations for solid state inorganic materials differ from those for organic molecules. In particular, periodic boundary conditions must be applied for solid state inorganic materials, and non-localized plane wave basis sets are applied instead of the localized Gaussian-type basis sets. The Bloch’s theorem states that the wave functions in periodic systems can be expressed as Bloch waves, and the wave functions of any free electrons can be described with plane wave packets. The most widely accepted calculation programs are VASP and CASTEP, and functionals are PBE for solid state calculations, while for molecular calculations, the programs are GAUSSIAN and functionals are B3LYP.
From the view points of a simulator, one can calculate every property including the structure, the total energy, and the band structure of a substance. Two of the most important properties of a cathode material obtainable from the first principles calculations are structure and energy, which determine the voltage, capacity, and cycling stability of the Li-ion batteries.
Meng et al. [10] have reviewed the computation approaches aimed at designing better electrode materials for Li-ion batteries, especially how each relevant property can be related to the structural component in the material and can be computed from the first principles. Recently, they also reviewed the first-principles computational investigations toward understanding, controlling, and improving the intrinsic properties of five well known high energy density Li-ion intercalation electrode materials: layered oxides (LiMO2), spinel oxides (LiM2O4), olivine phosphates (LiMPO4), silicates (Li2MSiO4), and the tavorite (LiM(XO4)F), where M are 3d transition metal elements. They described the crystal structures, the redox potentials, the ion mobilities, the possible phase transformation mechanisms, and structural stability changes, and the relevance of these properties to the development of high-energy, high-power, low-cost electrochemical systems [11]. 2.1 Phosphates
The olivine LiFePO4 is one of the most competitive cathode materials for Li-ion batteries attributing to its relatively high energy density, and excellent thermal and electrochemical stability, environmental friendliness, and low cost. However, the large scale commercialization of LiFePO4 in electric vehicles is impeded by its poor electrode kinetics or charging/discharging kinetics because of the low Li-ions migration rate.
The crystal defects are important factors impacting Li-ion transport mechanism and pathways. Hoang et al. [12] studied the native point defects and defect complexes in LiFePO4 using DFT calculation within the GGA + U framework and concluded that the native point defects were charged, and each defect was stable in one charge state only. Kuss et al. [13] investigated site exchange defects in LiFePO4 and FePO4, as well as the energies and diffusion kinetics using atomistic modeling based on empirical force field model.
Doping and substitution are two important methods widely accepted for the improvement of LiFePO4 in experiments. In order to explain the mechanism of doping and substitution, Xu et al. [14] investigated the electronic structures of pure and doped LiFePO4 by the first-principles calculations and concluded that the band-gap of LiFePO4 was most affected by F-ion doping at O site with the narrowest band gap, followed by Mn-ion doping at Fe site, and Na-ion doping at Li site. Lin et al. [15] calculated the average intercalation voltage and charging/discharging volume change of LiMnxCo1-xPO4 and concluded that the volume change of LiMnxCo1-xPO4 to MnxCo1-xPO4 was smaller than that of undoped LiCoPO4 which was responsible for the excellent tolerance of repeated cycling in Li-ion batteries.
Besides the doping on the metallic sites or O sites, the substitution of the phosphorus atoms by other elements, such as carbon atoms, will also affect the properties of LiFePO4. Chen et al. [16] discovered a new class of carbon phosphates, which could intercalate Li-ions reversibly from a novel high-throughput ab initio computational approach, and reported their synthesis, characterization, and electrochemical testing. The systematic experimental validation of the carbon phosphates were conducted, and experimental conditions of formation and the computational results were compared and discussed [17]. On the other hand, Xu et al. [18] studied the effect of C doping on the structural and electronic properties of LiFePO4 using the first-principles calculations within the GGA + U framework and indicated that C doped at O sites was energetically favored, and that C dopants preferred to occupy O3 sites.
Since the LiMPO4 (M = Mn, Ni, Co, V) is unstable at high temperature by releasing oxygen via disproportionation reactions, which may result in the explosion of the Liion batteries. Therefore, it is reasonable to use the disproportionation products, the pyrophosphates as cathode materials. The properties of Li9M3(P2O7)3(PO4)2 (M = V, Mo), potentially interesting cathodes from a highthroughput computational search, were studied with DFT calculations. From the calculated voltage, volume change, stability, safety, and diffusivity, it was found that extracting the final Li from LixV3(P2O7)3(PO4)2 will be difficult due to voltage and safety concerns, while the yet-unreported class of compounds LixV3-3yMo3y(P2O7)3(PO4)2 was proposed as a potential improvement over the pure V compound, especially for y = 2/3 [19]. 2.2 Complex oxides
The lithium transition-metal oxides LiMO2 (M = Co, Ni, Mn), such as LiMnO2 and LiCoO2, are the most widely applied cathode materials in the early age and are still widely accepted for Li-ion batteries. The defect chemistry in a series of layered lithium transition-metal oxides, LiMO2 (M = Co, Ni, Mn, and Li1/3Mn2/3), was investigated by systematic first-principles calculations. The calculations clearly showed that Ni3+ ions in LiNiO2 were easily reduced, whereas Mn3+ ions in LiMnO2 were easily oxidized under ordinary high-temperature synthesis conditions [20]. A first-principles approach to predict the intercalation voltage for lithium in metal oxides was presented, and the intercalation voltage of LiMO2 (M = Ti, V, Co, Ni and Cu) was computed in good agreement with experimental observations [21].
DFT calculations were also applied to the investigation of delithiation process, the kinetics of lithium diffusion, and the oxygen stability of Li2MnO3 [22]. The surface structure and equilibrium particle shape of the LiMn2O4 spinel were studied from DFT calculations which were benchmarked to obtain the correct semiconducting, Jahn-Teller distorted ground state of bulk LiMn2O4 [23]. Combined computational and experimental studies were used to probe the active redox pairs and changes in electronic structure of LiNi1/3Co1/3Mn1/3O2 during intercalation or deintercalation of Li, and concluded that LiNi1/3Co1/3Mn1/3O2 was a highcapacity stable cathode material for Li-ion batteries [24]. In another investigation, Ling et al. [25] studied the Li and Li oxides insertion in a-MnO2 with the first-principles calculations.
Besides defects structures, Kim et al. [26] studied the thermodynamic stability of oxygen and lithium vacancies and their most stable configurations of layered lithium nickel oxide based cathode materials by DFT calculations. The Jahn-Teller effect in LiNiO2, LiMnO2, and LiCuO2, were investigated in the framework of GGA, and the cooperative distortion was decomposed into the symmetrized- strain modes and k = 0 optical phonons [27]. 2.3 Silicates and borates
Besides the complex oxides and phosphates, silicates and borates are also investigated using the first principles calculations. Liivat demonstrated that the full reversal of Li/Fe site occupations was energetically favored on delithiation for all three electrochemically active Li2FeSiO4 polymorphs, and the common layered topology in the arrangement of SiO4 and FeO4 tetrahedra in all three polymorphs transforms into a 3D-framwork. However, the partial reversal is energetically less favored supporting the twophase transformation mechanism [28]. Seo et al. [29] studied the polymorphism and phase transformations of Li2-xFeSiO4 (0 ≤ x ≤ 2) from the first principles calculations. In addition, the structural and electrochemical properties of the different polymorphs of Li2MnSiO4 were studied [30]. The Li intercalation potential, volume change, and Li mobility of LiMBO3 (M = Mn, Fe, and Co) were also studied [31].
Manthiram described the challenges and prospects associated with high-voltage and high-capacity cathode as well as high-capacity anode materials, and the approaches to overcome these challenges were presented including computational modeling and simulations [32]. 3 Band-gap calculations
Band-gap, which is the energy gap between occupied and unoccupied states, is an essential property for semiconductors, and electrochemical, optical, and photovoltaic materials. The band-gap can also be interpreted as the difference between the ionization energy and electron affinity energy [33]. The experimentally measured bandgaps are sensitive to local structure and defects of the surface via photoemission spectroscopy, optical absorption spectroscopy, and cyclic voltammetry. Such error should be taken into account in any cautious comparison of experimental and theoretical band-gaps. The calculated band-gaps are very sensitive to the physical models and approximations. The Hartree-Fock self-consistent field approximation usually overestimates the band-gap, and the typical DFT approximations underestimate the band-gap. Therefore, various approximations, including time-dependent DFT, exact exchange, hybrid and screened-hybrid functionals, and modified Becke-Johnson potentials, are developed to accurately evaluate band-gaps [34].
Recently, Ceder et al. generalized the delta self-consistent- field (DSCF) method to predict the band-gaps for solids, and 70 % reduction of mean absolute errors compared to the Kohn-Sham gaps on over 100 compounds with experimental gaps of 0.5-4 eV, at computational costs similar to typical DFT calculations were obtained [34]. For the transition metal and rare-earth compounds, the DFT + U method which is used to address the on-site Coulomb interactions in the localized d or f orbitals with an additional Hubbard-type term U, is widely accepted [35, 36, 37]. The GGA + U method often correctly reproduces the relative energetic, magnetic ground states, and electronic structure for systems in which GGA often fails, including redox reaction energies in oxides for which GGA may produce errors of over 1 eV per formula unit. However, the GGA + U method also suffers from limitations, especially the transferability of U across compounds. Jain calculated the formation enthalpies for a test set of 49 ternary oxides by mixing GGA and GGA + U method, and the mean absolute relative error was reduced from 7.7 % to 21 % in GGA + U method to under 2 % [38]. Recently, a novel nonempirical scaling correction method was developed to tackle the challenge of band-gap prediction in DFT calculations [39]. 4 Phase diagram calculations
Phase diagrams are essential for the development of new materials. It is also very tedious to experimentally measure the phase diagram of a multicomponent system, such as ternary and quarternary systems. The CALPHAD techniques have permitted the prediction of phase diagrams and thermodynamic properties of multicomponent systems from binary and ternary subsystems. Since the DFT is an important method for the calculation of thermodynamic properties, phase diagrams can be calculated by combination of CALPHAD and DFT methods.
Based on the first principles calculations, Ong et al. [40] calculated the phase diagram of Li-Fe-P-O2. They also investigated the thermal reduction of delithiated LiMnPO4 and LiFePO4 based on the quarternary phase diagrams and confirmed that MnPO4 decomposed at much lower temperature than FePO4, and substantial oxygen was released as MnPO4 reduced to Mn2P2O7 [41]. In addition, they compared the small polaron migration and phase separation in olivine LiMnPO4 and LiFePO4 using the HSE06 functional [42]. 5 Kinetic mechanisms and rate processes
Any commercial Li-ion batteries should be charged in reasonable time. The charging speed of a battery is evaluated in C-rate which is the multiple of the current over the current that the battery can be fully charged from its fully discharged state in one hour. At discharging, the battery is used to supply power for loadings. The discharging speed of the battery is also evaluated in C-rate which is the multiple of the current over the current that the battery can sustain for one hour. No matter in charging or in discharging, the maximum obtainable C-rate of any battery is limited by its technical condition, and the maximum charging/discharging C-rate is an intrinsic technical parameter determining the minimum time in which the battery can be charged and/or the maximum power that the battery can supply. For the application in the transportation and electricity storage sectors, the maximum charging/ discharging C-rate is one of the most important restrictive parameters.
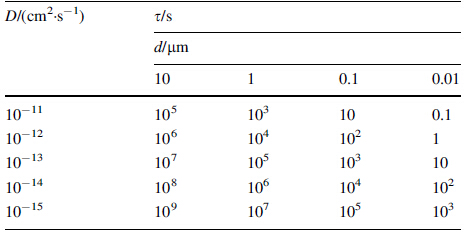
The maximum charging/discharging C-rate of a battery is determined by the intrinsic characteristics of the battery materials, as well as its design and technical conditions. During charging/discharging of a Li-ion battery, the ratedetermining step is usually the intercalation/extraction of Li-ions into/from the cathode material. For a cathode material with diffusion coefficient D and particle diameter d, the Li-ions can be fully intercalated or extracted in an average time of τ = d2/D. The typical apparent Li-ion diffusion coefficient D in LiFePO4 is from 10-13 cm2/s to 10-14 cm2/s. If the average particle size of LiFePO4 is 1 lm, the average intercalation/extraction time of all the Li-ions will be from 104 s to 105 s, equivalent to a maximum C-rate from 0.36 °C to 0.036 °C. From Table 1, where it lists a few typical Li-ion diffusion time τ at various diffusion coefficients D and particle diameters d, it can be concluded why the particles of cathode materials must be reduced to nanoscale.
 |
It is well known that the thermodynamic properties are state variables independent on the preparation history as well as the shapes and morphologies of the material if its surface effects are neglected. The redox voltages are thermodynamic properties dependent only on the intrinsic properties of the material and independent on its preparation history. Therefore, the voltage and specific energy of a Li-ion battery are only dependent on its electrode materials. However, the apparent diffusion coefficient of an electrode material is not a state variable and dependent on its preparation history as well as the shapes and morphologies of the material particles. It can be concluded that the charging/discharging characteristics of a electrode material is related to the diffusion coefficient and particle sizes and morphologies, and the control of particle sizes and morphologies is the most important issue in the preparation of electrode materials for Li-ion batteries satisfying fast charging/discharging.
In this section, we are going to overview the experimental techniques, as well as theoretical methods for the evaluation of apparent diffusion coefficients of Li-ions in cathode materials. We will present the experimental techniques and their applications in Sect. 5.1. In Sect. 5.2, we will discuss the theoretical methods that are used to investigate the Li-ions diffusion mechanism including diffusion pathways and activation energies by DFT calculations and various molecular dynamics (MD) simulations. In addition, technical means for the improvement of diffusion kinetics by introducing of disorders and defects and dopants are proposed. 5.1 Measurements of apparent Li-ion diffusion coefficients
The apparent Li-ion diffusion coefficient in an electrode can be evaluated using various experimental techniques including cyclic voltammetry (CV), electrochemical impedance spectroscopy (EIS), the ratio of the potentiocharge capacity to the galvano-charge capacity method (RPG), galvanostatic intermittent titration technique (GITT), potentiostatic intermittent titration techniques (PITT), and capacity intermittent titration technique (CITT) [43a, 44]. For example, Tang et al. [45] investigated the diffusion behavior of Li-ions in LiFePO4 by CITT, and determined continuously the Li-ion diffusion coefficient D in LiMn2O4 using CITT [46, 47]. Churikov evaluated the Li-ion diffusion coefficient in LiFePO4 by GITT and PITT [48].
The Li-ion diffusion coefficient in thin film of LiFePO4 prepared by radio frequency magnetron sputtering is in range of 10-14 cm2/s to 10-12 cm2/s and 10-15 cm2/s to 10-12 cm2/s measured by PITT and EIS, respectively, and in order of 10-14 cm2/s measured by CV [49]. In the same work, it was concluded that the Li-ion diffusion coefficient was dependent greatly on electrode potential but almost independent on the Ag content in the LiFePO4 film and crystal orientation, and thicker films show somewhat larger diffusion coefficients than thinner films. In addition, the electrochemical performance is determined mainly by the electronic conductivity of the films, rather than by the Liion diffusion kinetics [49]. Tang et al. [50] deposited a pure, well crystallized and highly (0 3 3) oriented LiCoO2 thin film on stainless steel substrate by pulsed laser deposition and measured the apparent Li-ion diffusion coefficient to be between 2 × 10-13 cm2/s and 10-12 cm2/s using CV, EIS, and PITT.
The apparent diffusion coefficient of Li-ions in LixFePO4 is also dependent on its composition or the value of x, as the value of x changes from 0 to 1. The apparent diffusion coefficient varies from 2.2910-16 cm2/s to 1.8910-14 cm2/s evaluated by EIS and GITT techniques [51]. Recently, we prepared nano-layered LiFePO4 particles from nano-layered ferrous phenylphosphonate templates, and observed the apparent Li-ion diffusion coefficient at 1.5 × 10-11 cm2/s and 3.1 × 10-13 cm2/s by CV and EIS, respectively. These values are among the best apparent Li-ion diffusion coefficients ever observed in LixFePO4 [52]. 5.2 DFT investigation of Li-ion diffusion mechanisms
DFT calculations are powerful tools not only for the calculations of energetics and the optimization of structures, but also for the investigation of transport mechanisms. Dathar et al. [53] studied the Li-ion migration pathways in olivine Li1-xFePO4 using the DFT + U method, and resolved the discrepancy between experimental measurements and theoretical calculations by considering various possible Li-ion diffusion kinetics, including diffusions in the bulk, on the surface, in the presence of defects, and in varying local environments, and concluded that the slow vacancy diffusion, which had a barrier of 0.71 eV, compared to 0.29 eV in defect-free channels, was the most important factor to the slow Li-ion kinetics. Hoang et al. studied the effect of various dopants, including monovalent (Na, K, Cu, and Ag), divalent (Mg and Zn), trivalent (Al), tetravalent (Zr, C, and Si), and pentavalent (V and Nb), on the ionic and electronic conductivities of LiFePO4 from DFT calculations, and identified impurities that were effective (or ineffective) at enhancing of concentration of lithium vacancies or of small hole polarons. They also discussed specific strategies for enhancing of electrical conductivity in LiFePO4, and provided suggestions for further experimental studies [54].
Liu et al. [55] studied the Li-ion migration properties, especially the activation energies in the olivine structured Li1-xFePO4 and in the Li1-xFeSO4F using the nudged elastic band (NEB) method within the GGA + U framework. The calculated activation energies in LiFePO4 and FePO4 are 0.5 eV and 0.27 eV, respectively, and that in partially delithiated Li1-xFeSO4F is as low as 0.3 eV corresponding to a diffusion coefficient estimated to be about 1.6 × 10-7 cm2/s [56].
The effects of N doping on the crystal structure, charge distribution, and transport properties of N-doped LiFePO4 have been studied within the GGA + U framework. It was concluded that the Fe—N bonding was covalent like, and the Fe atom nearest to the N atom appeared as Fe3+ to maintain charge balance. These characteristics result in a much narrower band-gap and strongly localized band near the Fermi level, thus improved electronic conductivity. The Li-ion diffusion activation energy in N-doped LiFePO4 is slightly lower than the pristine LiFePO4 as evaluated using the NEB method [57]. The DFT calculations were also applied to the investigation of the (010) surface structure of LiFePO4 coated with graphene or graphene-like B—C—N, and two in-gap states with an interval of 0.6 eV appear in the gap resulting in improved electric conductivity [58].
Iddir and Curtiss studied the Li-ion diffusion mechanisms in bulk monoclinic Li2CO3 crystals using DFT calculations and concluded that Li-ions transported along the open channel along the [010] direction with potential barrier as small as 0.28 eV [59]. Kang carried out DFT calculations for the orthorhombic Li2NiO2 to study the Li-ion mobility and predicted that the activation barriers along the b-axis and diagonal direction between a- and b-axes were fairly low, ensuring the facile Li-ion diffusion along those directions. However, the migration along the a-axis is unlikely given the very high activation barrier, and thus it was concluded that Li2NiO2 was a reasonably good Li-ion conductor with 2D diffusion pathways [60]. 5.3 Atomistic simulations of Li-ion diffusion pathways
While DFT calculations are used to study the structures and energetics of Li-ion transport, MD simulations are used to directly simulate the transport pathways of Li-ions. Lee et al. [61] carried out MD simulations based on empirical potential parameters to elucidate the structure, defect chemistry, and Li-ion transport pathways and dynamics in Li2MP2O7 (M = Mn, Fe, and Co), and concluded that the pyrophosphates without partial occupation had a 2D Li-ion transport pathway. Meanwhile, under the condition of partial occupancies of Li and transition metal atoms, the diffusion pathway of Li-ion is a 3D network [61]. For the monoclinic Li3V2(PO4)3, the Li-ion mobility is fairly high and strongly anisotropic as revealed by migration energy calculation, and the Li-ion diffusion coefficients are evaluated to be about 10-11 cm2/s (at 298 K) with activation energy of 0.45-0.48 eV based on MD simulations [62]. For LiFePO4, Adams simulated the Li-ion transport pathways as regions of low bond valence mismatch based on empirical force field models [63]. While classical MD simulations depending on empirical force field models, Yang et al. investigated the Li-ion diffusion mechanisms in fully lithiated LiFePO4 with spin polarized ab initio molecular dynamics calculations (AIMD) within GGA + U framework and concluded that Li-ion diffusion was not a continuous process but a series of jumps from one site to another. A dominant process is the jumping between neighboring Li sites around the PO4 groups resulting in a zigzag pathway along the crystallographic b-axis and a second process involves the collaborative movements of the Fe-ions leading to the formation of antisite defects and promotes Li-ion diffusion across the Li-ion channels [64]. And the AIMD simulations indicated that the lithium layer was the main diffusion plane in Li2MnO3, while the Li-ions in the transition-metal LiMn2 layer migrated into the lithium layer first, and then diffused through the lithium plane or moved back to the LiMn2 layer [22].
The DFT calculations and AIMD simulations have also been combined to study the diffusion mechanism of Li-ions in the olivine LiFePO4 and to simulate the 1D diffusion behavior [65]. In addition, Ouyang et al. [66] calculated the migration energy barriers of Li-ions and Cr-ions along the 1D diffusion pathway in pure and Cr-doped LiFePO4 from the first principles calculations, and then applied Monte Carlo simulations to evaluate the influences of the blocking behaviors on the electrochemical performance of LiFePO4. 5.4 Direct observation of Li-ion diffusion pathways
The direct observation and visualization of Li-ion transport pathways in LixFePO4 were realized by combining hightemperature powder neutron diffraction and the maximum entropy method [67]. Recently, Clark et al. [68] studied the Li-ion transport pathways in high-voltage pyrophosphate cathode materials by combination of atomistic simulation and neutron diffraction techniques and concluded that the Li-ion diffusion in Li2FeP2O7 would follow nonlinear, curved pathways parallel to the b- and c-axes through a 2D network in the bc-plane in contrast to the 1D diffusion in LiFePO4. In addition, favorable doping was for Na+ on the Li+ site, and isovalent dopants (e.g., Mn2+, Co2+, Cu2+) on the Fe2+ site. In contrast, supervalent doping especially V5+ and Nb5+ appears unfavorable on both Li+ and Fe2+ sites. 6 Materials for sodium ion batteries
If large scale commercializations of electric vehicles and energy storage facilitates based on Li-ion batteries are realized, the sustainable supply of lithium may be a great problem as the lithium reserves in China are limited and mainly locate in the environmentally weak area of Qinghai Province. Therefore, alternative technologies based on the Na-ion batteries, working on the cheap and widely accessible sodium, were proposed.
The principles for Na-ion batteries are similar to that of Li-ion batteries. In the core of a Na-ion battery, there are the cathode material and the anode material separated by a microporous membrane soaked in nonaqueous electrolyte solution allowing the shuttling of Na-ions between the two electrode materials. The requirements for anode material, the electrolyte solution, and the microporous membrane used in Na-ion batteries differ slightly from those used in Li-ion batteries. What makes really different is the cathode material. The cathode material used in Na-ion batteries must allow the reversible intercalation and extraction of Na-ions which are more spacious than the Li-ions. In this section, we are going to review the recent theoretical investigations of Na-ion intercalation materials with an emphasis on the transport mechanisms.
As an emerging technology, the number of Na-ion intercalation materials is limited and their structures resemble to that of Li-ion intercalation materials. For example, Velikokhatnyi et al. [69, 70] studied the structural stability of NaBxMn1-xO2 (x = 0-0.375) and that with 75 % vacancy of Na-ions for each concentration of B using DFT calculations within the GGA framework. Recently, Kim et al. [71] studied the structural and electrochemical properties of Na0.44MnO2 by the first principles calculations combined with experiments, and suggested that the Cr substitution will reduce the volume change significantly during intercalation and extraction.
The sodium iron fluorophosphates are also investigated as Na-ion intercalation materials. Ramzan et al. [72] studied the crystal structures of Li2FePO4F, Na2FePO4F, LiFePO4F, and NaFePO4F by ab initio calculations in the framework of GGA and GGA + U, and the calculated intercalation voltages with the GGA + U method was in good agreement with experimental values. New iron-based mixed polyanion compounds LixNa4-xFe3(PO4)2(P2O7) (x = 0-3) were synthesized, and their crystal structures were determined. The first principles calculations have identified the complex 3D pathways as well as the corresponding activation barriers and revealed these materials as fast ionic conductors. The properties of high power, small volume change, and high thermal stability were also recognized, presenting this type of new compounds as potential competitors to other iron-based electrodes such as Li2FeP2O7, Li2FePO4F, and LiFePO4 [73]. In addition, the NEB method with eight images along the Na-ion migration pathway was used to evaluate the sodium migration barriers in Na2FeP2O7 [74]. The Na2MnP2O7, as a new cathode material for Na-ion batteries, was investigated using both experimental and theoretical methods with the firstprinciples calculations to study the structure and intercalation kinetics [75].
Recently, Na3V2(PO4)2F3 was studied with combined first principles and experimental method for rechargeable Na-ion batteries, and the mechanism of structural evolution and the electrochemical behavior upon battery cycling [76]. 7 Combination of data mining and high-throughput ab initio calculations
The benefits from DFT calculations in the design and optimization of new materials have been demonstrated across several research fields. The scalability of computations makes it possible to make predictions on thousands of compounds, and potentially for all known inorganic materials. For example, Jain et al. [77] described a highthroughput infrastructure for DFT calculations to compute properties of approximately 80, 000 compounds within the GGA + U framework.
Recently, the concept of MGP, materials design by the combination of high-throughput computation and database mining of all known inorganic materials, was proposed [4]. As an example of MGP, the design of electrode materials for Li-ion batteries was demonstrated, and several new electrode materials were computationally designed and experimentally synthesized and tested [4]. Besides the high-throughput first principles computing, the other technology for the MGP is the data mining, searching crystal structure database for candidate materials. For example, Ceder et al. [78] searched experimental or computational results and applied the data mining results to the prediction of crystal structure of materials.
Now the database searching algorithms have developed into machine learning, and it is possible to predict unknown or unidentified compounds that do not exist in any databases. Using a probabilistic model built on an experimental crystal structure database, Tautier et al. [79] identified 209 novel compositions that were most likely to form a compound, predicted their most-probable crystal structures, and tested for their stability by DFT computations. Bennett integrated database searching and the first principles calculations for the discovery and design of novel functional materials [80].
Substitution is an important method in the discovery of new compounds. Hautier et al. developed a probabilistic model assessing the likelihood for ionic species to substitute for each other while retaining the crystal structure. The model was trained on an experimental database of crystal structures, and could be used to quantitatively suggest novel compounds and their structures. The predictive power of the model was demonstrated using crossvalidation on quaternary ionic compounds. The different substitution rules embedded in the model were analyzed and compared to some of the traditional rules used by solid state chemists to propose new compounds [81].
Hautier et al. applied high-throughput ab initio computing to study a series of mixed polyanions compounds of formula AxM(YO3)(XO4) (with A = Na, Li; X = Si, As, P; Y = C, B; M = a redox active metal; and x = 0-3). The stability of both lithium and sodium-based compounds was analyzed along with the voltage, specific energy, and energy density, and several novel carbonophosphates and carbonosilicates were identified as potential high capacity ([200 mAh/g) and specific energy ([700 Wh/kg) cathode materials for Li-ion batteries [82]. In addition, highthroughput DFT calculations were also applied in the study of phosphates [83], tavorite-structured oxyphosphates, fluorophosphates, oxysulfates, and fluoro sulfates [84], and complex oxides LiMO2 (M = Ti, V, Mn, Co, Ni, Zn) for their applications as cathode materials [85, 86].
Recently, several review articles were published in the field of materials design by combination of intelligent data mining and high-throughput ab initio calculations, and the challenges and opportunities of this rapidly developing field were highlighted [87, 88, 89]. 8 Conclusions
In the past years, we have witnessed the exponential growth of computing technology and its penetration into every aspects of modern society. Computing technology is also changing the development activities of new materials. One of the most significant achievements is the development of the first principles calculation methods and programs which allow the experimentalists to calculate or predict the structures and properties of a material or compound before its synthesis. The second achievement is the development of atomistic modeling techniques which allow the visualization of the motion of atoms, molecules, and even chemical reaction processes. These techniques will inspire scientists and engineers to develop and optimize the preparation process of new materials. The third achievement is the development of various databases of crystals and compounds allowing the fast searching for any experimental information that has ever accumulated.
One of the challenges is to integrate the first principles calculations, atomistic modeling, and databases into a single system, so that streamlined development of new materials, screening candidate compounds or predicting unknown compounds, calculating their properties, and visualizing their synthesis reactions, can be realized. The second challenge is to develop new functionals to accurately calculate electron correlation energy, and thus other properties and energies.
Acknowledgements The authors thank the National Natural Science Foundation of China (Grant Nos. 21073118, 21376147), the Innovation Program of Shanghai Municipal Education Commission (Grant No. 13ZZ078), and the 085 Knowledge Innovation Program for the financial support, and they also acknowledge the Laboratory for Microstructures, Shanghai University, for carrying out the structural characterization.| 1. | Padhi AK, Nanjundaswamy KS, Goodenough JB (1997) Phospho- olivines as positive-electrode materials for rechargeable lithium batteries. J Electrochem Soc 144:1188-1194 |
| 2. | Chung SY, Bloking JT, Chiang YM (2002) Electronically conductive phospho-olivines as lithium storage electrodes. Nat Mater 1:123-128 |
| 3. | Eagar TW (1995) Bringing new materials to market. Technol Rev 98:42-49 |
| 4. | Ceder G (2010) Opportunities and challenges for first-principles materials design and applications to Li battery materials. Mater Res Soc Bull 35:693-701 |
| 5. | Hafner J (2008) Ab-initio simulations of materials using VASP: density-functional theory and beyond. J Comput Chem 29:2044-2078 |
| 6. | Perdew JP, Burke K, Ernzerhof M (1996) Generalized gradient approximation made simple. Phys Rev Lett 77:3865-3868 |
| 7. | Adamo C, Barone V (1999) Toward reliable density functional methods without adjustable parameters: the PBE0 model. J Chem Phys 110:6158-6170 |
| 8. | Heyd J, Scuseria GE, Ernzerhof M (2003) Hybrid functionals based on a screened coulomb potential. J Chem Phys 118:8207-8215 |
| 9. | Krukau AV, Vydrov OA, Izmaylov AF, Scuseria GE (2006) Influence of the exchange screening parameter on the performance of screened hybrid functionals. J Chem Phys 125:224106 |
| 10. | Meng YS, Arroyo-de Dompablo ME (2009) First principles computational materials design for energy storage materials in lithium ion batteries. Energy Environ Sci 2:589-609 |
| 11. | Meng YS, Arroyo-de Dompablo ME (2013) Recent advances in first principles computational research of cathode materials for lithium-ion batteries. Acc Chem Res 46:1171-1180 |
| 12. | Hoang K, Johannes M (2011) Tailoring native defects in LiFe- PO4: insights from first-principles calculations. Chem Mater 23:3003-3013 |
| 13. | Kuss C, Liang G, Schougaard SB (2012) Atomistic modeling of site exchange defects in lithium iron phosphate and iron phosphate. J Mater Chem 22:24889-24893 |
| 14. | Xu J, Chen G (2010) Effects of doping on the electronic properties of LiFePO4: a first-principles investigation. Phys B 405:803-807 |
| 15. | Lin ZP, Zhao YM, Zhao YJ (2011) First-principles studies of Mndoped LiCoPO4. Chin Phys B 20:018201-018206 |
| 16. | Chen H, Hautier G, Jain A, Moore C, Kang B, Doe R, Wu L, Zhu Y, Tang Y, Ceder G (2012) Carbonophosphates: a new family of cathode materials for Li-ion batteries identified computationally. Chem Mater 24:2009-2016 |
| 17. | Chen H, Hautier G, Ceder G (2012) Synthesis, computed stability, and crystal structure of a new family of inorganic compounds: carbonophosphates. J Am Chem Soc 134:19619-19627 |
| 18. | Xu GG, Wu J, Chen ZG, Lin YB, Huang ZG (2012) Effect of C doping on the structural and electronic properties of LiFePO4: a first-principles investigation. Chin Phys B 21:097401 |
| 19. | Jain A, Hautier G, Moore C, Kang B, Lee J, Chen H, Twu N, Ceder G (2012) A computational investigation of Li9M3 (P2O7)3(PO4)2 (M = V, Mo) as cathodes for Li ion batteries. J Electrochem Soc 159:A622-A633 |
| 20. | Koyama Y, Arai H, Tanaka I, Uchimoto Y, Ogumi Z (2012) Defect chemistry in layered LiMO2 (M = Co, Ni, Mn, and Li1/3Mn2/3) by first-principles calculations. Chem Mater 24:3886-3894 |
| 21. | Aydinol MK, Kohan AF, Ceder G (1997) Ab initio calculation of the intercalation voltage of lithium-transition-metal oxide electrodes for rechargeable batteries. J Power Sour 68:664-668 |
| 22. | Xiao R, Li H, Chen L (2012) Density functional investigation on Li2MnO3. Chem Mater 24:4242-4251 |
| 23. | Karim A, Fosse S, Persson KA (2013) Surface structure and equilibrium particle shape of the LiMn2O4 spinel from firstprinciples calculations. Phys Rev B 87:075322 |
| 24. | Hwang BJ, Tsai YW, Carlier D, Ceder G (2003) A combined computational/experimental study on LiNi1/3Co1/3Mn1/3O2. Chem Mater 15:3676-3682 |
| 25. | Ling C, Mizuno F (2012) Capture lithium in a-MnO2: insights from first principles. Chem Mater 24:3943-3951 |
| 26. | Kim Y, Kim D, Kang S (2011) Experimental and first-principles thermodynamic study of the formation and effects of vacancies in layered lithium nickel cobalt oxides. Chem Mater 23:5388-5397 |
| 27. | Marianetti CA, Morgan D, Ceder G (2001) First-principles investigation of the cooperative Jahn-Teller effect for octahedrally coordinated transition-metal ions. Phys Rev B 63:224304 |
| 28. | Liivat A (2012) Structural changes on cycling Li2FeSiO4 polymorphs from DFT calculations. Solid State Ion 228:19-24 |
| 29. | Seo D-H, Kim H, Park I, Hong J, Kang K (2011) Polymorphism and phase transformations of Li2-xFeSiO4 (0 B x B 2) from first principles. Phys Rev B 84:220106 |
| 30. | Kalantarian MM, Asgari S, Mustarelli P (2013) Theoretical investigation of Li2MnSiO4 as a cathode material for Li-ion batteries: a DFT study. J Mater Chem A 1:2847-2855 |
| 31. | Seo DH, Park YU, Kim SW, Park I, Shakoor RA, Kang K (2011) First-principles study on lithium metal borate cathodes for lithium rechargeable batteries. Phys Rev B 83:205127 |
| 32. | Manthiram A (2011) Materials challenges and opportunities of lithium ion batteries. J Phys Chem Lett 2:176-184 |
| 33. | Godby RW, Garc'?a-Gonz'alez P (2003) A primer in density functional theory. Springer, Berlin, p 256 |
| 34. | Chan MKY, Ceder G (2010) Efficient band gap prediction for solids. Phys Rev Lett 105:196403 |
| 35. | Wang L, Maxisch T, Ceder G (2006) Oxidation energies of transition metal oxides within the GGA + U framework. Phys Rev B 73:195107 |
| 36. | Rohrbach A, Hafner J, Kresse G (2003) Electronic correlation effects in transition-metal sulfides. J Phys 15:979 |
| 37. | Anisimov VI, Zaanen J, Andersen OK (1991) Band theory and Mott insulators: Hubbard U instead of stoner I. Phys Rev B 44:943-954 |
| 38. | Jain A, Hautier G, Ong SP, Moore CJ, Fischer CC, Persson KA, Ceder G (2011) Formation enthalpies by mixing GGA and GGA + U calculations. Phys Rev B 84:045115 |
| 39. | Zheng X, Cohen AJ, Mori-Sánchez P, Hu X, Yang W (2011) Improving band gap prediction in density functional theory from molecules to solids. Phys Rev Lett 107:026403 |
| 40. | Ong SP, Wang L, Kang B, Ceder G (2008) LiFePO2 phase diagram from first principles calculations. Chem Mater 20:1798-1807 |
| 41. | Ong SP, Jain A, Hautier G, Kang B, Ceder G (2010) Thermal stabilities of delithiated olivine MPO4 (M = Fe, Mn) cathodes investigated using first principles calculations. Electrochem Commun 12:427-430 |
| 42. | Ong SP, Chevrier VL, Ceder G (2011) Comparison of small polaron migration and phase separation in olivine LiMnPO4 and LiFePO4 using hybrid density functional theory. Phys Rev B 83:075112 |
| 43. | Tang K, Yu X, Sun J, Li H, Huang X (2011) Kinetic analysis on LiFePO4 thin films by CV, GITT, and EIS. Electrochim Acta 56:4869-4875 |
| 44. | Tang XC, Pan CY, He LP, Li LQ, Chen ZZ (2004) A novel technique based on the ratio of potentio-charge capacity to galvano- charge capacity (RPG) for determination of the diffusion coefficient of intercalary species within insertion-host materials: theories and experiments. Electrochim Acta 49:3113-3119 |
| 45. | Tang XC, Li LX, Lai QL, Song XW, Jiang LH (2009) Investigation on diffusion behavior of Li+ in LiFePO4 by capacity intermittent titration technique (CITT). Electrochim Acta 54:2329-2334 |
| 46. | Tang XC, Song XW, Shen PZ, Jia DZ (2005) Capacity intermittent titration technique (CITT): a novel technique for determination of Li+ solid diffusion coefficient of LiMn2O4. Electrochim Acta 50:5581-5587 |
| 47. | Montella C (2006) Comments of the paper 'capacity intermittent titration technique (CITT). A novel technique for determination of Li+ solid diffusion coefficient of LiMn2O4' [X.-C. Tang, X.-W. Song, P.-Z. Shen, D.-Z. Jia, Electrochim. Acta 50 (2005) 5581-5587]. Electrochim Acta 51:2778-2781 |
| 48. | Churikov AV, Ivanishchev AV, Ivanishcheva IA, Sycheva VO, Khasanova NR, Antipov EV (2010) Determination of lithium diffusion coefficient in LiFePO4 electrode by galvanostatic and potentiostatic intermittent titration techniques. Electrochim Acta 55:2939-2950 |
| 49. | Xie J, Imanishi N, Zhang T, Hirano A, Takeda Y, Yamamoto O (2009) Li-ion diffusion kinetics in LiFePO4 thin film prepared by radio frequency magnetron sputtering. Electrochim Acta 54: 4631-4637 |
| 50. | Tang SB, Lai MO, Lu L (2008) Li-ion diffusion in highly (0 3 3) oriented LiCoO2 thin film cathode prepared by pulsed laser deposition. J Alloys Compd 449:300-303 |
| 51. | Prosini PP, Lisi M, Zane D, Pasquali M (2002) Determination of the chemical diffusion coefficient of lithium in LiFePO4. Solid State Ion 148:45-51 |
| 52. | Chen J, Yan L, Yue B (2012) Nano-layered LiFePO4 particles converted from nano-layered ferrous phenylphosphonate templates. J Power Sour 209:7-14 |
| 53. | Dathar GKP, Sheppard D, Stevenson KJ, Henkelman G (2011) Calculations of Li-ion diffusion in olivine phosphates. Chem Mater 23:4032-4037 |
| 54. | Hoang K, Johannes MD (2012) First-principles studies of the effects of impurities on the ionic and electronic conduction in LiFePO4. J Power Sour 206:274-281 |
| 55. | Liu Z, Huang X (2010) Factors that affect activation energy for Li diffusion in LiFePO4: a first-principles investigation. Solid State Ion 181:907-913 |
| 56. | Liu Z, Huang X (2012) Structural, electronic and Li diffusion properties of LiFeSO4F. Solid State Ion 181:1209-1213 |
| 57. | Liu Z, Huang X, Wang D (2008) First-principle investigations of N doping in LiFePO4. Solid State Commun 147:505-509 |
| 58. | Sun C, Yan L, Yue B (2013) Improvement of surface structure and enhancement of conductivity of LiFePO4 surface by graphene and graphene-like B—XC—XN coating. Acta Phys Chim Sin 29:1666-1672 |
| 59. | Iddir H, Curtiss LA (2010) Li ion diffusion mechanisms in bulk monoclinic Li2CO3 crystals from density functional studies. J Phys Chem C 114:20903-20906 |
| 60. | Kang K, Morgan D, Ceder G (2009) First principles study of Li diffusion in I-Li2NiO2 structure. Phys Rev B 79:014305 |
| 61. | Lee S, Park SS (2012) Structure, defect chemistry, and lithium transport pathway of lithium transition metal pyrophosphates (Li2MP2O7, M: Mn, Fe, and Co): atomistic simulation study. Chem Mater 24:3550-3557 |
| 62. | Lee S, Park SS (2012) Atomistic simulation study of monoclinic Li3V2(PO4)3 as a cathode material for lithium ion battery: structure, defect chemistry, lithium ion transport pathway, and dynamics. J Phys Chem C 116:25190-25197 |
| 63. | Adams S (2010) Lithium ion pathways in LiFePO4; and related olivines. J Solid State Electrochem 14:1787-1792 |
| 64. | Yang J, Tse JS (2011) Li ion diffusion mechanisms in LiFePO4: an ab initio molecular dynamics study. J Phys Chem A 115: 13045-13049 |
| 65. | Ouyang C, Shi S, Wang Z, Huang X, Chen L (2004) First-principles study of Li ion diffusion in LiFePO4. Phys Rev B 69:4303 |
| 66. | Ouyang CY, Shi SQ, Wang ZX, Li H, Huang XJ, Chen LQ (2004) The effect of Cr doping on Li ion diffusion in LiFePO4 from first principles investigations and Monte Carlo simulations. J Phys 16:2265 |
| 67. | Nishimura SI, Kobayashi G, Ohoyama K, Kanno R, Yashima M, Yamada A (2008) Experimental visualization of lithium diffusion in LixFePO4. Nat Mater 7:707-711 |
| 68. | Clark JM, Nishimura SI, Yamada A, Islam MS (2012) Highvoltage pyrophosphate cathode: insights into local structure and lithium-diffusion pathways. Angew Chem 51:13149- 13153 |
| 69. | Velikokhatnyi OI, Choi D, Kumta PN (2006) Effect of boron on the stability of monoclinic NaMnO2: theoretical and experimental studies. Mater Sci Eng B 128:115-124 |
| 70. | Velikokhatnyi OI, Chang CC, Kumta PN (2004) Ab initio calculations and structural stability of boron-doped sodium manganese oxide. J Electrochem Soc 151:J8-J13 |
| 71. | Kim H, Kim DJ, Seo DH, Yeom MS, Kang K, Kim DK, Jung Y (2012) Ab initio study of the sodium intercalation and intermediate phases in Na0.44MnO2 for sodium-ion battery. Chem Mater 24:1205-1211 |
| 72. | Ramzan M, Lebegue S, Ahuja R (2009) Ab initio study of lithium and sodium iron fluorophosphate cathodes for rechargeable batteries. Appl Phys Lett 94:151904 |
| 73. | Kim H, Park I, Seo DH, Lee S, Kim SW, Kwon WJ, Park YU, Kim CS, Jeon S, Kang K (2012) New iron-based mixed-polyanion cathodes for lithium and sodium rechargeable batteries: combined first principles calculations and experimental study. J Am Chem Soc 134:10369-10372 |
| 74. | Kim H, Shakoor RA, Park C, Lim SY, Kim JS, Jo YN, Cho W, Miyasaka K, Kahraman R, Jung Y et al (2013) Na2FeP2O7 as a promising iron-based pyrophosphate cathode for sodium rechargeable batteries: a combined experimental and theoretical study. Adv Funct Mater 23:1147-1155 |
| 75. | Park CS, Kim H, Shakoor RA, Yang E, Lim SY, Kahraman R, Jung Y, Choi JW (2013) Anomalous manganese activation of a pyrophosphate cathode in sodium ion batteries: a combined experimental and theoretical study. J Am Chem Soc 135: 2787-2792 |
| 76. | Shakoor RA, Seo DH, Kim H, Park YU, Kim J, Kim SW, Gwon H, Lee S, Kang K (2012) A combined first principles and experimental study on Na3V2(PO4)2F3 for rechargeable Na batteries. J Mater Chem 22:20535-20541 |
| 77. | Jain A, Hautier G, Moore CJ, Ping Ong S, Fischer CC, Mueller T, Persson KA, Ceder G (2011) A high-throughput infrastructure for density functional theory calculations. Comput Mater Sci 50:2295-2310 |
| 78. | Ceder G, Morgan D, Fischer C, Tibbetts K, Curtarolo S (2006) Data-mining-driven quantum mechanics for the prediction of structure. MRS Bull 31:981-985 |
| 79. | Hautier G, Fischer CC, Jain A, Mueller T, Ceder G (2010) Finding nature's missing ternary oxide compounds using machine learning and density functional theory. Chem Mater 22: 3762-3767 |
| 80. | Bennett JW (2012) Discovery and design of functional materials: integration of database searching and first principles calculations. Phys Proc 34:14-23 |
| 81. | Hautier G, Fischer C, Ehrlacher V, Jain A, Ceder G (2011) Data mined ionic substitutions for the discovery of new compounds. Inorg Chem 50:656-663 |
| 82. | Hautier G, Jain A, Chen H, Moore C, Ong SP, Ceder G (2011) Novel mixed polyanions lithium-ion battery cathode materials predicted by high-throughput ab initio computations. J Mater Chem 21:17147-17153 |
| 83. | Hautier G, Jain A, Ong SP, Kang B, Moore C, Doe R, Ceder G (2011) Phosphates as lithium-ion battery cathodes: an evaluation based on high-throughput ab initio calculations. Chem Mater 23:3495-3508 |
| 84. | Mueller T, Hautier G, Jain A, Ceder G (2011) Evaluation of favorite-structured cathode materials for lithium-ion batteries using high-throughput computing. Chem Mater 23:3854-3862 |
| 85. | Ceder G, Aydinol MK, Kohan AF (1996) Application of firstprinciples calculations to the design of rechargeable Li-batteries. Comput Mater Sci 8:161-169 |
| 86. | Ceder G, Chiang YM, Sadoway DR, Aydinol MK, Jang YI, Huang B (1998) Identification of cathode materials for lithium batteries guided by first-principles calculations. Nature 392:694-696 |
| 87. | Curtarolo S, Hart GLW, Nardelli MB, Mingo N, Sanvito S, Levy O (2013) The high-throughput highway to computational materials design. Nat Mater 12:191-201 |
| 88. | Hautier G, Jain A, Ong S (2012) From the computer to the laboratory: materials discovery and design using first-principles calculations. J Mater Sci 47:7317-7340 |
| 89. | Ceder G, Hautier G, Jain A, Ong S (2011) Recharging lithium battery research with first-principles methods. MRS Bull 36:185-191 |
 2014, Vol. 2
2014, Vol. 2




