文章信息
- 王佳敏, 刘秋萍, 巩超, 张明露, 高培, 唐迅, 胡永华.
- Wang Jiamin, Liu Qiuping, Gong Chao, Zhang Minglu, Gao Pei, Tang Xun, Hu Yonghua
- 离散事件模拟模型在流行病学筛查成本效果分析中的应用
- Application of discrete event simulation model in analysis on cost-effectiveness of epidemiology screening
- 中华流行病学杂志, 2023, 44(3): 463-469
- Chinese Journal of Epidemiology, 2023, 44(3): 463-469
- http://dx.doi.org/10.3760/cma.j.cn112338-20220725-00659
-
文章历史
收稿日期: 2022-07-25
2. 北京大学医学信息学中心, 北京 100191
2. Medical Informatics Center, Peking University, Beijing 100191, China
理论流行病学的决策模型可评价筛查等干预措施的长期效果,并开展成本效果分析,为公共卫生决策提供依据[1]。在复杂疾病筛查效果的评价中,马尔科夫模型因其“无记忆性”和人群同质性的假设,通常难以评估个体的特征和疾病史对疾病进展的影响[2];微观模拟模型(microsimulation model)基于个体进行模拟,弥补了马尔科夫模型的上述缺陷,但其本质上仍是状态转换模型,即通过模拟固定周期内个体的状态转换情况反映疾病进展,不可避免会受到固定周期的限制,因而无法精确估计事件发生的时间[3]。离散事件模拟(discrete event simulation,DES)模型可通过模拟发生在不同时间的各个离散事件的情况来反映疾病进展,近年来在医疗健康领域的应用越来越广泛,例如用于评估乳腺癌筛查效果等研究[4-5]。DES模型特别适用于需要考虑时间维度的复杂筛查和干预策略的评价,如根据个体的特征采用不同筛查频率[6-7]。本文详细介绍DES模型的基本原理、构建与分析步骤,并结合实例讨论DES模型在流行病学筛查成本效果分析中的应用。
一、基本原理DES模型又称为事件发生时间模型(time-to-event model)[5],是一种基于个体模拟的模型,通过从事件发生时间的分布中抽样,模拟个体在一定时限内的各离散事件发生情况,来反映疾病的发生发展过程[8]。DES模型的核心要素包括事件(events)、属性(attributes)和时钟(clock),事件用来表示个体在模拟过程中发生的各种情况,如疾病的进展或缓解、某项筛查或干预措施的实施、个体健康行为的改变等[9];属性指的是个体的特征(如年龄、健康状况等),可影响模型中事件的发生情况并随时间变化而更新;时钟用于记录模型运行时间,当个体发生一个事件后,时钟延展到该事件的时间点,然后更新属性并继续模拟下一个事件发生情况,直至个体死亡后退出模型或达到设定的模拟时限[10]。
1. 模型构建与参数收集:研究者在构建DES模型前,应详细描述研究问题和建模目的,模型构建的结构需要反映研究疾病的发生发展过程与需决策的问题,可采用流程图呈现模型的核心要素,例如事件发生的可能路径及先后关系、模拟过程中的决策节点等。
DES模型收集的参数:①个体属性的参数;②疾病进程相关的参数;③干预措施效应强度的参数;④成本、健康效用值、贴现率等经济学参数。研究者应根据指南的推荐按照一定规范选择参数,并需要对参数的来源和选择依据进行说明,当模型参数具有多个不同来源时,需综合考虑模型参数来源的证据等级、人群特征及地区差异等,尽可能与模型模拟的情景一致[9]。
2. 模型分析:
(1) 创建个体:DES模型在创建模拟个体时需确定模拟人数并定义个体初始属性。在目前的算力下,百万级的模拟人数已经足够,可使模型结果趋于稳定[11]。定义个体初始属性的方法:①从流行病学调查人群的汇总特征中抽样;②使用现实人群的个体数据[10]。前者的优点在于数据的可获得性更好,但该方法较难考虑个体不同属性间的关联性;后者的数据虽可反映不同属性之间的关联,但通常难获取适合的数据资源。
(2) 情景模拟:情景模拟的核心包括模拟个体的事件发生与属性更新情况[10]。事件发生的时间通常服从特定的分布,主要包括指数分布、威布尔分布、冈珀茨(Gompertz)分布等,可根据风险函数(hazard function)和生存函数(survival function)的特点选择分布[12]。在选择何种分布时,可通过图示法判断事件发生时间服从的参数分布,也可直接使用指数分布、威布尔分布、冈珀茨分布等对生存数据分别进行拟合,并通过拟合优度检验来选择适当的分布,拟合分布时还可纳入个体的特征作为预测变量,以反映个体属性对事件发生时间的影响。确定事件发生时间服从的分布后,通过从各事件发生时间的分布中随机抽样模拟个体事件发生的时间。
对于个体而言,同一时间可面临多种事件发生的选择,通过随机数抽样模拟多种事件的发生时间,选择发生时间最早的事件作为个体经历的事件。当个体发生事件后,时钟更新至该事件发生的时间,并更新个体的属性,继续进行下一个事件的模拟,直至个体死亡或者达到设定的模拟时限。DES模型分析的流程见图 1。

|
| 图 1 离散事件模拟模型分析的流程图 |
(3) 基础分析:进行成本效果分析时,模型的输出结果主要为成本、生命年、质量调整生命年(QALY)和事件发生数。DES模型将记录个体发生的事件及时间,并计算相应的成本、生命年和QALY,当所有个体完成模拟后,汇总计算人群的平均成本和效果指标,通过不同筛查策略下模型汇总结果的比较,计算增量成本-效果比(incremental cost-effectiveness ratio,ICER),用于评价筛查的成本效果[9]。
3. 敏感性分析:与其他决策模型类似,DES模型针对模型参数的不确定性对结果影响的分析方法主要包括确定性敏感性分析(deterministic sensitivity analysis,DSA)和概率敏感性分析(probabilistic sensitivity analysis,PSA)[13]。DSA主要评价模型中特定的一个或一组参数的变化对结果的影响,并针对参数的变化范围给出模型结果相应的变化范围。PSA主要评价多个参数变化的不确定性,参数根据其服从的分布随机抽样产生,通过蒙特卡罗模拟的方法重复抽样计算模型结果的置信区间。
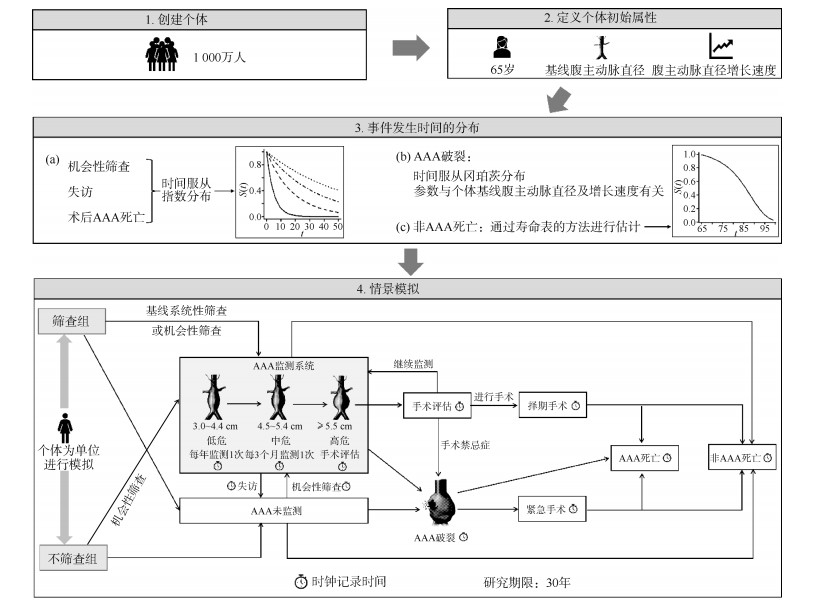
二、研究实例以《柳叶刀》上发表的在英国≥65岁女性人群中开展的腹主动脉瘤(abdominal aortic aneurysm,AAA)筛查的成本效果分析为例[14],介绍DES模型的构建过程和分析方法。该研究中使用的DES模型将腹主动脉的直径处理为随时间变化的连续变量,并根据动脉的直径对个体采用不同的筛查频率,因而适用于评价与时间有关的复杂筛查和干预策略的成本效果[14-15]。限于篇幅,本文仅讨论“65岁开始筛查、腹主动脉直径达到3 cm诊断AAA、直径达到5.5 cm进行手术干预”这一筛查策略相比于不开展系统性筛查的成本效果,DES模型分析的原始代码(https://github.com/mikesweeting/AAA_DES_model)已在R 4.1.3软件中完成结果复现。
1. 模型构建:该实例考虑的疾病为AAA,目标人群为英国≥65岁的女性,评估的干预策略为随时间变化的AAA筛查。实例中的腹主动脉直径数据来源于英国国家AAA筛查项目(National Abdominal Aortic Aneurysm Screening Programme),采用蒙特卡罗模拟的方法从基线特征(包括年龄、基线腹主动脉直径及直径随时间增长的速度)的分布中抽样产生1 000万基线年龄均为65岁的女性人群,模拟时限为30年,直至个体达到95岁或者死亡。首先创建个体并根据腹主动脉直径的分布抽样分配个体的属性,直径随时间增长的速度服从与基线直径相关的条件分布,并通过混合线性模型估计[16]。DES模型需估计发生时间的事件及其主要假设:①机会性筛查、失访、AAA死亡的时间服从指数分布,分布的参数为相应事件的发生率;②AAA破裂的时间服从冈珀茨分布,分布的参数与个体的基线腹主动脉直径及其增长速度有关;③非AAA死亡的时间分布通过寿命表的方法根据不同年龄段的死亡率估计。见图 2。
模型模拟的情景包括筛查组和不筛查组,两组的个体都有可能经历机会性筛查,但基线时仅在筛查组对所有个体开展系统性筛查。筛查时采用超声测量腹主动脉直径,直径达到3.0 cm将被诊断为AAA而进入监测系统。在AAA监测系统中,直径为3.0~4.4 cm的个体测量频率为每年1次,4.5~5.4 cm为每3个月1次,当直径≥5.5 cm将启动手术评估,此时使用影像学检查再次测量AAA直径,若直径≥5.5 cm且无手术禁忌症者将择期手术。患有AAA的个体可能发生瘤体破裂,可能将进行紧急手术,也可能未手术而死亡。手术期间死亡、术后与AAA相关的死亡及AAA破裂导致的死亡均定义为AAA死亡事件,其他原因的死亡则定义为非AAA死亡事件。
上述DES模型的构建在R语言中主要通过自定义函数实现(表 1)。个体的情景模拟通过自定义的processOnePair()函数实现,包括创建列表记录个体的经历和成本效果指标、从初始属性的分布中抽样、设置并更新个体发生的事件和时间、计算个体的成本和效果指标。
2. 模型分析:
(1) 基础分析:DES模型在计算机编程实现过程中,单线程通常在前一个体完成模拟后,后一个体才继续进入模型进行模拟,直至所有个体的模拟结束,但也可通过多线程处理减少模拟的运算时间,例如在该实例中,通过自定义的processPersons()函数实现了多线程处理,模拟所有研究对象在筛查组和不筛查组分别经历的事件和时间,并计算人群平均的成本和效果指标。首先设置种子数为2(原作者代码中的设定),通过setAndshowRandomSeed()函数可产生一系列用于个体抽样的种子数,再使用parLapply()函数多线程运行所有个体processOnePair()函数的结果,以获得所有个体在筛查组和不筛查组分别经历的事件和时间、成本和QALY,最后根据研究对象在两个组的平均成本和QALY计算ICER。英国人群的ICER的阈值定为20 000英镑,即低于该阈值则认为筛查策略具有成本效果。
(2) 敏感性分析:采用单因素敏感性分析探索模型主要参数的不确定性对结果的影响,例如AAA的患病率、机会性筛查率和失访率、筛查和监测的成本以及手术的成本,通过每次仅修改一个相应的参数后重新运行DES模型实现。概率敏感性分析采用蒙特卡罗模拟的方法,可使用psa()函数实现:首先从参数的分布中随机抽样,产生1 000组参数,然后分别模拟在每组参数下所有个体运行processPersons()函数的结果,输出结果为1 000次模拟后的平均成本、QALY和ICER,并取2.5%和97.5%的结果作为95%CI的范围。
3.结果解读:基础分析的结果发现,在英国≥65岁的女性人群中进行AAA筛查相比于不筛查,能减少2 590例(3.08%)AAA死亡,每预防1例AAA死亡需筛查3 862人;筛查组和不筛查组的平均成本分别为84.16和50.11英镑,平均QALY分别为10.449 5和10.448 3年,计算ICER发现每增加一个QALY而增加的成本为28 975(95%CI:12 760~1 000 513)英镑,大于阈值的20 000英镑。单因素敏感性分析发现,AAA患病率对ICER的影响较大,当患病率增加一倍时ICER可减少至12 548英镑/QALY,患病率减少一半时ICER将增加至65 686英镑/QALY;概率敏感性分析发现ICER < 20 000英镑阈值的概率仅为17.6%。因此,在英国≥65岁的女性人群中开展AAA筛查相比于不筛查,并不具有成本效果优势。
三、总结和展望DES模型在心血管病[14]、恶性肿瘤[17-18]、糖尿病肾病[19]等复杂疾病的筛查项目评价中的应用越来越广泛。在上述AAA筛查的研究实例中,疾病的进展过程及筛查干预措施均相对复杂,DES模型可将复杂过程转变为对一系列离散事件发生的情景模拟,模型的适用性较强。首先,对于竞争事件(如该实例中的AAA死亡和非AAA死亡),DES模型将竞争风险大小转变为事件发生时间,通过选择发生时间较早的事件实现对竞争事件发生的模拟;其次,对于筛查中常见的假阳性问题,该实例的DES模型中分别设定筛查与金标准采用的测量方法,通过添加相应的离散事件,从而较好地实现此类复杂但重要问题的情景模拟;最后,对于个体特征随时间变化的问题,DES模型可将特征处理为连续变量,并模拟其对疾病进展和筛查干预措施的影响,如该实例中的DES模型可实现AAA的监测频率随直径变化而改变的情景模拟。因此,DES模型由于其基于个体对离散事件的发生情况进行模拟,且能够较好地处理个体特征和事件与时间维度的关系,特别适合模拟复杂筛查措施的评价。
马尔科夫模型和微观模拟模型也是成本效果分析常用的决策模型,其原理是通过设置特定状态和固定周期,分析研究对象的状态转换以模拟疾病进展,与DES模型存在较大差异(表 2)。DES模型中事件发生的时间是通过从分布中抽样获得,并不设定固定的周期,因而对时间的处理更加灵活。与马尔科夫模型相比,DES模型是基于个体的模型,不受马尔科夫模型“无记忆性”的局限,可以考虑个体特征和疾病史与疾病发生发展的关系。基于个体的微观模拟模型作为状态转换模型仍会受到固定的状态转换周期限制,对事件发生时间的估计不够精确,而DES模型则不受该限制,且不需要模拟未发生事件的空白时间,因而效率更高。
尽管DES模型在模拟疾病发生发展上具有许多优势,但在实际应用上仍然存在局限性,其中最重要的就是需要足够的数据来建立各种事件发生时间的分布函数,这也是DES模型准确模拟的关键所在。另外,DES模型对建模者的数学背景要求也更高,需要对概率分布和相关统计学方法有较深的理解[6]。目前可用于实现DES模型的软件较多,如通用的开源软件R、Python等,常用的决策分析软件TreeAge也有相应的模块可将事件发生时间作为节点(node)嵌入决策树用于构建DES模型,便于可视化展示。无论采用何种软件,为保证研究的透明度和可重复性,均需要清晰地展现模型结构及构建过程,并遵循相应的报告规范开展流行病学筛查的成本效果分析[20]。
综上所述,DES模型基于个体数据,通过模拟离散事件的发生情况来反映疾病进展,不仅可以考虑个体特征对疾病进展的影响,还不受固定周期的限制,能较好地处理个体特征和事件与时间的关系,特别适用于考虑时间维度的复杂疾病筛查及干预策略的长期效果评价。
利益冲突 所有作者声明无利益冲突
作者贡献声明 王佳敏:实施研究、统计分析、论文撰写;刘秋萍、巩超、张明露:采集数据、统计分析、论文审阅;高培:论文审阅;唐迅:设计研究、实施研究、论文撰写;胡永华:设计研究、论文审阅
| [1] |
Atkinson JA, Page A, Prodan A, et al. Systems modelling tools to support policy and planning[J]. Lancet, 2018, 391(10126): 1158-1159. DOI:10.1016/S0140-6736(18)30302-7 |
| [2] |
刘秋萍, 高培, 唐迅, 等. 马尔可夫模型在流行病学筛查成本效果分析中的应用[J]. 中华流行病学杂志, 2021, 42(4): 728-734. Liu QP, Gao P, Tang X, et al. Applications of Markov model for cost-effectiveness analysis of screening in epidemiology[J]. Chin J Epidemiol, 2021, 42(4): 728-734. DOI:10.3760/cma.j.cn112338-20200729-00993 |
| [3] |
刘秋萍, 王佳敏, 巩超, 等. 微观模拟模型在流行病学筛查成本效果分析中的应用[J]. 中华流行病学杂志, 2022, 43(6): 931-937. Liu QP, Wang JM, Gong C, et al. Applications of microsimulation model for cost-effectiveness analysis on screening in epidemiology[J]. Chin J Epidemiol, 2022, 43(6): 931-937. DOI:10.3760/cma.j.cn112338-20210802-00601 |
| [4] |
Zhang X. Application of discrete event simulation in health care: a systematic review[J]. BMC Health Serv Res, 2018, 18(1): 687. DOI:10.1186/s12913-018-3456-4 |
| [5] |
Vázquez-Serrano JI, Peimbert-García RE, Cárdenas-Barrón LE. Discrete-event simulation modeling in healthcare: a comprehensive review[J]. Int J Environ Res Public Health, 2021, 18(22): 12262. DOI:10.3390/ijerph182212262 |
| [6] |
Caro JJ, Möller J. Advantages and disadvantages of discrete-event simulation for health economic analyses[J]. Expert Rev Pharmacoecon Outcomes Res, 2016, 16(3): 327-329. DOI:10.1586/14737167.2016.1165608 |
| [7] |
Caro JJ, Möller J, Getsios D. Discrete event simulation: the preferred technique for health economic evaluations?[J]. Value Health, 2010, 13(8): 1056-1060. DOI:10.1111/j.1524-4733.2010.00775.x |
| [8] |
Karnon J, Stahl J, Brennan A, et al. Modeling using discrete event simulation: a report of the ISPOR-SMDM modeling good research practices task force-4[J]. Value Health, 2012, 15(6): 821-827. DOI:10.1016/j.jval.2012.04.013 |
| [9] |
刘国恩. 中国药物经济学评价指南2020[M]. 北京: 中国市场出版社, 2020. Liu GE. China guidelines for pharmacoeconomic evaluations 2020[M]. Beijing: China Market Press, 2020. |
| [10] |
Caro JJ, Möller J, Karnon J, et al. Discrete event simulation for health technology assessment[M]. New York: Chapman and Hall/CRC, 2015.
|
| [11] |
Siebert U, Alagoz O, Bayoumi AM, et al. State-transition modeling: a report of the ISPOR-SMDM modeling good research practices task force-3[J]. Value Health, 2012, 15(6): 812-820. DOI:10.1016/j.jval.2012.06.014 |
| [12] |
Kleinbaum DG, Klein M. Survival analysis: a self-learning text[M]. 3rd ed. New York: Springer, 2012.
|
| [13] |
Briggs AH, Weinstein MC, Fenwick EAL, et al. Model parameter estimation and uncertainty: a report of the ISPOR-SMDM modeling good research practices task force-6[J]. Value Health, 2012, 15(6): 835-842. DOI:10.1016/j.jval.2012.04.014 |
| [14] |
Sweeting MJ, Masconi KL, Jones E, et al. Analysis of clinical benefit, harms, and cost-effectiveness of screening women for abdominal aortic aneurysm[J]. Lancet, 2018, 392(10146): 487-495. DOI:10.1016/S0140-6736(18)31222-4 |
| [15] |
US Preventive Services Task Force. Screening for abdominal aortic aneurysm: US Preventive Services Task Force recommendation statement[J]. JAMA, 2019, 322(22): 2211-2218. DOI:10.1001/jama.2019.18928 |
| [16] |
The RESCAN Collaborators. Surveillance intervals for small abdominal aortic aneurysms: a meta-analysis[J]. JAMA, 2013, 309(8): 806-813. DOI:10.1001/jama.2013.950 |
| [17] |
Lee CI, Cevik M, Alagoz O, et al. Comparative effectiveness of combined digital mammography and tomosynthesis screening for women with dense breasts[J]. Radiology, 2015, 274(3): 772-780. DOI:10.1148/radiol.14141237 |
| [18] |
Campbell LA, Blake JT, Kephart G, et al. Understanding the effects of competition for constrained colonoscopy services with the introduction of population-level colorectal cancer screening: a discrete event simulation model[J]. Med Decis Making, 2017, 37(2): 253-263. DOI:10.1177/0272989X16670638 |
| [19] |
Willis M, Asseburg C, Slee A, et al. Development and internal validation of a discrete event simulation model of diabetic kidney disease using CREDENCE trial data[J]. Diabetes Ther, 2020, 11(11): 2657-2676. DOI:10.1007/s13300-020-00923-w |
| [20] |
Husereau D, Drummond M, Augustovski F, et al. Consolidated health economic evaluation reporting standards 2022 (CHEERS 2022) statement: updated reporting guidance for health economic evaluations[J]. BMJ, 2022, 376: e067975. DOI:10.1136/bmj-2021-067975 |
 2023, Vol. 44
2023, Vol. 44