文章信息
- 李卫霞, 曹莉, 张德昊, 蔡畅, 黄丽菊, 赵建农, 宁毅.
- Li Weixia, Cao Li, Zhang Dehao, Cai Chang, Huang Liju, Zhao Jiannong, Ning Yi
- 新型冠状病毒Omicron变异株BA.5.1.3亚型潜伏期研究
- Study of incubation period of infection with 2019-nCoV Omicron variant BA.5.1.3
- 中华流行病学杂志, 2023, 44(3): 367-372
- Chinese Journal of Epidemiology, 2023, 44(3): 367-372
- http://dx.doi.org/10.3760/cma.j.cn112338-20221212-01060
-
文章历史
收稿日期: 2022-12-12
2. 三亚市疾病预防控制中心, 三亚 572000;
3. 海南医学院, 海口 571199;
4. 海南医学院第一附属医院, 海口 570102
2. Sanya Center for Disease Control and Prevention, Sanya 572000, China;
3. Hainan Medical University, Haikou 571199, China;
4. The First Affiliated Hospital of Hainan Medical University, Haikou 570102, China
新型冠状病毒(新冠病毒)感染大流行已造成全球6亿多人感染,约654万人死亡[1]。新冠病毒毒株经数次变异,Omicron变异株成为优势毒株[2-6]。2022年8月1日在海南省发现由Omicron变异株BA.5.1.3亚型引起的新冠病毒感染病例,截至2022年9月25日累计感染20 748例[7]。在病毒变异的过程中,变异株的潜伏期等流行病学特征也发生改变[8-10]。潜伏期是影响毒株在人群中传播强度、速度及基本传染数的重要指标,研究显示不同Omicron变异株的潜伏期也有所不同[11-15]。
在流行病学调查(流调)过程中,报告的感染时间有不精确现象,符合区间删失数据分布的特点,近年研究此类数据分布的理论和应用较多[9, 16-22],如对呼吸道传染病甲型流感和呼吸道合胞病毒感染的潜伏期估计[16]。区间删失数据也应用于2020年初出现的新冠病毒感染潜伏期估计[9, 21, 23],验证了该不确定性量化方法对于具有不精确数据的潜伏期估计的有效性,区间删失数据的贝叶斯估计成为估算潜伏期的有效方法[9, 20, 22],因此,本研究旨在利用区间删失数据的贝叶斯模型对三亚市疫情的潜伏期进行点估计和分布估计。
资料与方法1. 资料收集:源于三亚市新冠病毒Omicron变异株BA.5.1.3亚型感染者流调结果。按病例报告日期分析了2022年8月1-9日315例新冠病毒感染者流调记录。所有流调数据经过匿名化处理之后,选择其中信息用于研究分析,研究方案通过海南医学院生物医学伦理委员会批准(审批号:IRBGW20221205)。
2. 相关定义:从暴露到首次核酸阳性的检测时间区间定义为感染潜伏期,从暴露到报告临床症状出现的时间区间定义为发病潜伏期。感染者的信息包括首次核酸检测阳性时间、接触到上一代阳性感染者的时间、有明确的暴露时间点或有某段暴露区间。若患者没有明确的暴露时间点,则以患者自述的可能接触时间段定义为暴露区间。对于有症状感染者,若核酸检测阳性当天出现症状,则以当天作为发病时间点;若核酸检测阳性之前出现症状,则以报告症状到核酸检测阳性时间为区间;若核酸检测阳性之后出现症状,则以出现症状时间为发病时间点[22]。因此,计算潜伏期的数据结构有4种形式[16]:
第一种,假设E为感染者暴露的精确时间,S为感染者症状出现的精确时间,潜伏期(T)=S-E;
第二种,E为感染者暴露的精确时间,症状出现的时间为区间[SL,SR];
第三种,感染者暴露时间为区间[EL,ER],S为症状出现的精确时间;
第四种,暴露时间为区间[EL,ER],症状出现的时间为区间[SL,SR]。
第二、三、四种形式的数据结构是区间删失数据,第一、二、三种形式均可认为是第四种形式数据结构在区间上下限相同时的特例。
3. 分析方法:假设T是非负的连续随机变量,包括感染潜伏期和发病潜伏期,其概率密度函数为f (t,θ),其中θ为参数向量。本研究潜伏期采用常见的log-normal分布和Gamma分布。针对第四种形式的数据结构,log-normal分布的概率密度函数f (t,μ,σ) 的表达式:

式中,E采用均匀分布。
针对第一种形式的数据结构,Gamma分布概率密度函数为:
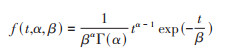
与log-normal分布同理,可表示出其他3种数据结构的Gamma分布概率密度函数,在此省略。
假设log-normal分布的两个参数的先验分布均服从正态分布,即
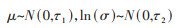
假设Gamma分布的两个参数α,β的先验分布为
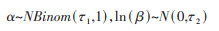
式中,NBinom是负二项分布。分别基于log-normal分布中参数μ,σ和Gamma分布中α,β的后验分布进行采样,得到潜伏期贝叶斯估计。
log-normal和Gamma两种分布在不同数据结构情况下,采用贝叶斯统计模型估计各分布参数的后验分布。针对后验分布存在计算复杂性问题,使用常用的离散时间马尔科夫链蒙特卡罗算法转移核Metropolis-Hastings算法对后验分布随机采样模拟,样本容量为10 000,设置种子数为123 456,得到潜伏期贝叶斯估计的分位数及95%CI。采用R 4.2.0软件的coarseDataTools包实现算法。
结果1. 基本特征:共纳入315例新冠病毒Omicron变异株BA.5.1.3亚型感染者流调数据,其中156例感染者在流行病学报告中记录了相关症状及其出现时间。暴露窗口的可能时间为2022年7月21日至8月6日,阳性检测结果的时间范围为2022年8月1-9日。315例感染者中27例为精确数据(第一种数据结构),238例为单区间删失数据(第二、三种数据结构),50例为双区间删失数据(第四种数据结构)。感染者年龄(42.01±16.54)岁;男性95例(30.16%),女性220例(69.84%)。有症状的156例感染者年龄(41.65±16.32)岁,男性44例(28.21%),女性112例(71.79%)。
2. 基于Omicron变异株BA.5.1.3亚型两种潜伏期分布的贝叶斯估计:
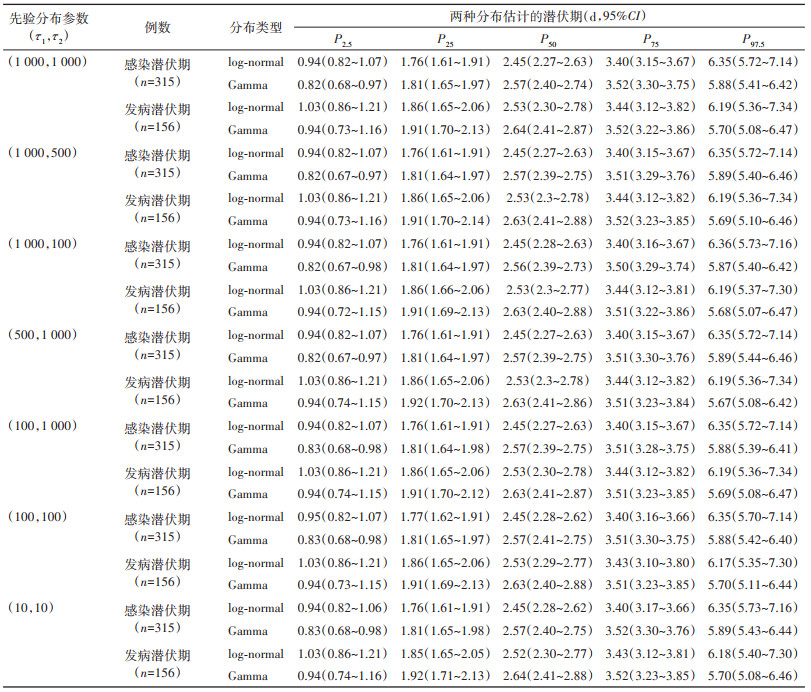
(1)发病潜伏期的估计:使用156例首次核酸检测阳性时出现症状感染者流调数据进行发病潜伏期估计。结果显示log-normal分布和Gamma分布在不同先验分布情况下,潜伏期分位数估计值的变化均在0.03范围内,P97.5的95%CI变化相差均小于0.05,表明发病潜伏期服从log-normal分布和Gamma分布时,参数不同先验分布的选择均对发病潜伏期估计影响较小,贝叶斯估计结果较稳健。见表 1。
当取相同的先验分布参数τ1=1 000,τ2=1 000时,得到log-normal分布和Gamma分布中参数采样的样本路径图和遍历均值图(图 1)。图 1A和图 1B的样本路径图显示,log-normal分布和Gamma分布的参数μ,σ及α,β的后验分布采样均是平稳的,不存在趋势性和周期性。从图 1C和图 1D的遍历均值图中均可见,马尔科夫链的各参数后验分布的采样在迭代4 000次后达到平稳状态。

|
| 图 1 发病潜伏期log-normal及Gamma分布参数采样的样本路径图和遍历均值图 |
基于采样平稳状态特征,将4个参数样本中4 001~10 000次取值的均值作为分布参数的估计值,即取log-normal分布的参数μ=0.93,σ=0.46,Gamma分布的参数α=5.23,β=0.55时,得到两分布估计的发病潜伏期的频率分布图。结果显示,基于log-normal分布和Gamma分布的潜伏期分布曲线拟合基本一致,提示贝叶斯估计比较稳定。在10 000次迭代后,log-normal分布和Gamma分布的对数似然函数值分别为-246.32和-243.24,Gamma分布对数似然函数值较大,三亚市2022年新冠病毒Omicron变异株BA.5.1.3亚型发病潜伏期最佳分布为Gamma分布。见图 2。
|
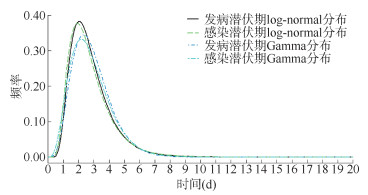
| 图 2 基于两种分布类型估计的两种潜伏期的频率分布 |
log-normal分布显示为正偏态分布,发病潜伏期M(Q1,Q3)为2.53(1.86,3.44)d,95%的病例潜伏期在5.41 d内,超过7、8、9、10 d的概率分别为1.36%、0.62%、0.29%、0.14%。Gamma分布的发病潜伏期M(Q1,Q3)为2.64(1.91,3.52)d,95%的病例潜伏期在5.21 d内,超过7、8、9、10 d的概率分别为0.59%、0.16%、0.04%、0.01%。
(2)感染潜伏期的估计:使用315例感染者流调数据进行感染潜伏期估计。结果显示log-normal分布和Gamma分布在不同先验分布情况下,潜伏期分位数估计值的变化均在0.02范围内,P97.5的95%CI变化相差最大仅0.06,表明感染潜伏期服从log-normal分布和Gamma分布时,参数不同先验分布的选择均对感染潜伏期估计影响较小,贝叶斯估计结果较稳健。见表 1。
类似发病潜伏期方法对感染潜伏期进行分析,当取相同的先验分布参数τ1=1 000,τ2=1 000时,从两种潜伏期分布的参数采样样本路径图和遍历均值图发现参数μ,σ及α,β的后验分布采样在迭代第4 000次后达到平稳状态,即取log-normal分布的参数μ=0.89,σ=0.49,Gamma分布的参数α=4.44,β=0.63时,得到两分布估计的频率分布图。结果显示,基于log-normal分布和Gamma分布的潜伏期分布曲线拟合基本一致,提示贝叶斯估计比较稳定。在10 000次迭代后,log-normal分布和Gamma分布的对数似然函数值分别为-112.62和-110.59,Gamma分布对数似然函数值较大,三亚市2022年新冠病毒Omicron变异株BA.5.1.3亚型感染潜伏期最佳分布为Gamma分布。见图 2。
log-normal分布显示为正偏态分布,感染潜伏期M(Q1,Q3)为2.45(1.76,3.40)d,95%的病例潜伏期在5.46 d内,超过7、8、9、10 d的概率分别为1.56%、0.76%、0.38%、0.20%。Gamma分布的感染潜伏期M(Q1,Q3)为2.57(1.81,3.52)d,95%的病例潜伏期在5.28 d内,超过7、8、9、10 d的概率分别为0.77%、0.24%、0.07%、0.02%。
讨论本研究根据三亚市新冠病毒感染者的暴露时间、症状出现时间和首次核酸检测阳性时间特征,利用区间删失数据的特点,建立常见潜伏期分布函数。本研究发现Omicron变异株BA.5.1.3亚型两种潜伏期分布均呈正偏态分布,感染潜伏期相比发病潜伏期M分别缩短0.08 d和0.07 d,相同潜伏期分布下中位数95%CI的上限最大相差0.15 d,无实际临床意义。Gamma分布估计感染潜伏期和发病潜伏期M分别为2.57 d和2.64 d。有小概率存在7~10 d的潜伏期,这种小概率事件在Omicron变异株感染防控中也不容忽视。
本研究使用的马尔科夫链蒙特卡罗算法对分布函数的参数进行贝叶斯估计的方法学是稳定的。Reich等[16]对甲型流感和呼吸道合胞病毒引起的呼吸道传染病的潜伏期估计所用的样本量分别为151例和24例,并通过仿真模拟结果验证了该方法的稳定性。Backer等[9]基于区间删失数据采用贝叶斯估计方法对2020年1月武汉市旅游者新冠病毒感染的潜伏期进行估计,证明了此方法的有效性。本研究的贝叶斯估计结果显示对于不同的先验分布的选择不敏感,支持现有模型估计的潜伏期是稳健的。
在Omicron变异株其他亚型的潜伏期研究中,Backer等[11]采用了确定的接触和症状时间数据估计了2021年12月荷兰发生的Omicron变异株BA.1亚型的潜伏期为3.20~4.40 d;Mefsin等[12]估计了我国香港地区暴发的Omicron变异株BA.1和BA.2亚型平均潜伏期分别为4.58 d和4.42 d,杜婧等[14]和黄勇等[15]估计了2022年3月我国北京市及2022年4月我国广州市发生的Omicron变异株潜伏期M分别为4 d和3 d。与以往的Omicron变异株相比,本研究估计的Omicron变异株BA.5.1.3亚型潜伏期M更短,说明2022年8月三亚市的Omicron变异株BA.5.1.3亚型传播速度更快。与2020年杜志成等[21]估计的Alpha变异株的log-normal分布和Gamma分布两种潜伏期M为4.94 d和5.06 d相比,是本研究估计的Omicron变异株BA.5.1.3亚型潜伏期的近2倍。
本研究存在局限性。首先,数据来源于感染者的流调报告,可能会受到感染者回忆偏差和调查质量的影响,但用于研究的疫情早期感染者的信息记录较全面,主要信息无缺失项,反映出早期调查的质量较高;其次,流调首先基于实验室诊断发现病例,在未报告症状的感染者中,可能出现未能准确记忆症状和尚未出现症状的情况,因此存在低估发病潜伏期的可能,但本研究有症状感染者占49.52%,高于2022年8月1日至9月25日的有症状感染者(42.13%),减少了低估发病潜伏期的可能。
本研究发现感染潜伏期和发病潜伏期M分别为2.57 d和2.64 d,提示此时间点前后是感染后核酸检测阳性和出现症状的主要时间窗口;同时,极少部分感染者的感染潜伏期和发病潜伏期长达7~10 d,较长的感染潜伏期和发病潜伏期也构成了疫情防控的难度和复杂性。本研究为Omicron变异株的疫情防控政策提供了真实世界依据。
利益冲突 所有作者声明无利益冲突
作者贡献声明 李卫霞、曹莉:数据分析、论文撰写/修改;张德昊、蔡畅、黄丽菊:采集/整理数据;赵建农、宁毅:研究指导、论文修改审阅、经费支持
志谢 感谢海南省疾病预防控制中心、三亚市疾病预防控制中心疫情防控组的大力支持
| [1] |
WHO. WHO CORONAVIRUS (COVID-19) DASHBOARD[EB/OL]. (2022-10-18)[2022-10-19]. https://covid19.who.int.
|
| [2] |
GISAID. Genomic epidemiology of SARS-CoV-2 with subsampling focused globally over the past 6 months[EB/OL]. (2022-10-14)[2022-10-19]. https://nextstrain.org/ncov/gisaid/global/6m.
|
| [3] |
Callaway E. Are COVID surges becoming more predictable? New Omicron variants offer a hint[J]. Nature, 2022, 605(7909): 204-206. DOI:10.1038/d41586-022-01240-x |
| [4] |
Cao YL, Yisimayi A, Jian FC, et al. BA. 2.12. 1, BA. 4 and BA. 5 escape antibodies elicited by Omicron infection[J]. Nature, 2022, 608(7923): 593-602. DOI:10.1038/s41586-022-04980-y |
| [5] |
黄云, 李依红, 谢仕兰, 等. 新型冠状病毒Omicron变异株研究进展[J]. 中华流行病学杂志, 2022, 43(5): 655-662. Huang Y, Li YH, Xie SL, et al. Progress in research of 2019-nCoV Omicron variant[J]. Chin J Epidemiol, 2022, 43(5): 655-662. DOI:10.3760/cma.j.cn112338-20220121-00061 |
| [6] |
廖春晓, 王波, 吕筠, 等. 新型冠状病毒Omicron变异株病原学及流行病学研究进展[J]. 中华流行病学杂志, 2022, 43(11): 1691-1698. Liao CX, Wang B, Lyu J, et al. Progress in research of etiology and epidemiology of 2019-nCoV Omicron variant[J]. Chin J Epidemiol, 2022, 43(11): 1691-1698. DOI:10.3760/cma.j.cn112338-20220929-00829 |
| [7] |
海南省卫生健康委员会. 截至9月25日24时海南省新型冠状病毒肺炎疫情最新情况[EB/OL]. (2022-09-26)[2022-10-19]. https://wst.hainan.gov.cn/swjw/rdzt/yqfk/202209/t20220926_3273195.html.
|
| [8] |
Weng YJ, Yi GY. Estimation of the COVID-19 mean incubation time: Systematic review, meta-analysis, and sensitivity analysis[J]. J Med Virol, 2022, 94(9): 4156-4169. DOI:10.1002/jmv.27841 |
| [9] |
Backer JA, Klinkenberg D, Wallinga J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20-28 January 2020[J]. Euro Surveill, 2020, 25(5): 2000062. DOI:10.2807/1560-7917.ES.2020.25.5.2000062 |
| [10] |
吴俣, 刘民. 不同新型冠状病毒变异株感染的COVID-19潜伏期研究[J]. 中国全科医学, 2022, 25(11): 1309-1313, 1319. Wu Y, Liu M. The incubation period of COVID-19 caused by different SARS-CoV-2 variants[J]. Chin General Pract, 2022, 25(11): 1309-1313, 1319. DOI:10.12114/j.issn.1007-9572.2022.0078 |
| [11] |
Backer JA, Eggink D, Andeweg SP, et al. Shorter serial intervals in SARS-CoV-2 cases with Omicron BA. 1 variant compared with Delta variant, the Netherlands, 13 to 26 December 2021[J]. Euro Surveill, 2022, 27(6): 2200042. DOI:10.2807/1560-7917.ES.2022.27.6.2200042 |
| [12] |
Mefsin YM, Chen DX, Bond HS, et al. Epidemiology of infections with SARS-CoV-2 Omicron BA. 2 variant, Hong Kong, January-March 2022[J]. Emerg Infect Dis, 2022, 28(9): 1856-1858. DOI:10.3201/eid2809.220613 |
| [13] |
于乐成, 宋勇. 新型冠状病毒Omicron变异株的病原学、临床特点、感染控制及治疗[J]. 解放军医学杂志, 2022, 47(11): 1063-1072. Yu LC, Song Y. Etiology, clinical features, infection control and therapy of SARS-CoV-2 Omicron variant[J]. Med J Chin Peoples Liberat Army, 2022, 47(11): 1063-1072. DOI:10.11855/j.issn.0577-7402.2022.11.1063 |
| [14] |
杜婧, 王佳敏, 王晶, 等. 北京市新型冠状病毒Omicron变异株的传播力研究[J]. 中华流行病学杂志, 2022, 43(9): 1364-1369. Du J, Wang JM, Wang J, et al. Study of transmissibility of 2019-nCoV Omicron variant in Beijing[J]. Chin J Epidemiol, 2022, 43(9): 1364-1369. DOI:10.3760/cma.j.cn112338-20220410-00274 |
| [15] |
黄勇, 郑志伟, 陈纯, 等. 广州市2起由新型冠状病毒Omicron变异株引起的本地疫情流行病学参数研究[J]. 中华流行病学杂志, 2022, 43(11): 1705-1710. Huang Y, Zheng ZW, Chen C, et al. Epidemiological characteristics of two local COVID-19 outbreaks caused by 2019-nCoV Omicron variant in Guangzhou, China[J]. Chin J Epidemiol, 2022, 43(11): 1705-1710. DOI:10.3760/cma.j.cn112338-20220523-00450 |
| [16] |
Reich NG, Lessler J, Cummings DAT, et al. Estimating incubation period distributions with coarse data[J]. Statist Med, 2009, 28(22): 2769-2784. DOI:10.1002/sim.3659 |
| [17] |
Zhang ZG, Sun JG. Interval censoring[J]. Stat Methods Med Res, 2010, 19(1): 53-70. DOI:10.1177/0962280209105023 |
| [18] |
Mcbryde ES, Gibson G, Pettitt AN, et al. Bayesian modelling of an epidemic of severe acute respiratory syndrome[J]. Bull Math Biol, 2006, 68(4): 889-917. DOI:10.1007/s11538-005-9005-4 |
| [19] |
Komárek A, Lesaffre E. Bayesian accelerated failure time model with multivariate doubly interval-censored data and flexible distributional assumptions[J]. J Am Stat Assoc, 2008, 103(482): 523-533. DOI:10.1198/016214507000000563 |
| [20] |
Hanson T, Johnson WO. A Bayesian semiparametric AFT model for interval censored data[J]. J Comput Graph Stat, 2004, 13(2): 341-361. DOI:10.1198/1061860043489 |
| [21] |
杜志成, 顾菁, 李菁华, 等. 基于区间删失数据估计方法的COVID-19潜伏期分布估计[J]. 中华流行病学杂志, 2020, 41(7): 1000-1003. Du ZC, Gu J, Li JH, et al. Estimating the distribution of COVID-19 incubation period by interval-censored data estimation method[J]. Chin J Epidemiol, 2020, 41(7): 1000-1003. DOI:10.3760/cma.j.cn112338-20200313-00331 |
| [22] |
邱明悦, 胡涛, 崔恒建. 双区间删失下新冠病毒肺炎潜伏期分布的参数估计[J]. 应用数学学报, 2020, 43(2): 200-210. DOI: CNKI:SUN:YYSU.0.2020-02-006. Qiu MY, Hu T, Cui HJ. Parametric estimation for the incubation period distribution of COVID-19 under doubly interval censoring[J]. Acta Mathemat Applict Sin, 2020, 43(2): 200-210. DOI: CNKI:SUN:YYSU.0.2020-02-006. |
| [23] |
Lu QB, Zhang Y, Liu MJ, et al. Epidemiological parameters of COVID-19 and its implication for infectivity among patients in China, 1 January to 11 February 2020[J]. Euro Surveill, 2020, 25(40): 2000250. DOI:10.2807/1560-7917.ES.2020.25.40.2000250 |
 2023, Vol. 44
2023, Vol. 44