文章信息
- 李卓颖, 沈秋明, 拓嘉怡, 唐丹丹, 肖宇轩, 赵龙刚, 项永兵.
- Li Zhuoying, Shen Qiuming, Tuo Jiayi, Tang Dandan, Xiao Yuxuan, Zhao Longgang, Xiang Yongbing
- 队列研究资料分析中Cox比例风险回归模型的时间尺度选择和应用
- Choice and application of time scale selection for Cox proportional hazards regression model in cohort studies
- 中华流行病学杂志, 2022, 43(12): 2002-2007
- Chinese Journal of Epidemiology, 2022, 43(12): 2002-2007
- http://dx.doi.org/10.3760/cma.j.cn112338-20220720-00644
-
文章历史
收稿日期: 2022-07-20
2. 上海交通大学医学院附属仁济医院上海市肿瘤研究所癌基因及相关基因国家重点实验室/流行病学研究室, 上海 200032;
3. 南卡罗莱纳大学阿诺德公共卫生学院流行病学与生物统计系, 哥伦比亚 29201
2. State Key Laboratory of Oncogene and Related Genes/Department of Epidemiology, Shanghai Cancer Institute, Renji Hospital, Shanghai Jiao Tong University School of Medicine, Shanghai 200032, China;
3. Department of Epidemiology & Biostatistics, Arnold School of Public Health, University of South Carolina, Columbia 29201, USA
Cox比例风险回归模型(Cox模型)是一种用于时间-事件数据分析的回归模型,是目前生存分析中重要的多因素分析方法,被广泛应用于临床随访研究、临床干预试验和流行病学前瞻性研究的资料分析中[1-2]。拟合Cox模型时一个关键的问题是如何选择合适的结局事件时间尺度。1979年Farewell和Cox[3]的研究指出,应当选择与结局事件关系最为密切的一个时间度量作为模型的时间尺度。在干预性质的临床研究中,结局事件的发生风险与接受干预的时间密切相关,采用治疗开始到结局出现的时间间隔(即随访时间)作为Cox模型的时间尺度,是十分自然、合理的。但在大多数观察性质的流行病学前瞻性研究,如队列研究中,研究起始的时间与观察结局之间一般来说并不存在直接关联,使用随访时间作为时间尺度可能并不完全合适[4-6]。由于年龄与许多疾病的发生密切相关,近年来有学者主张用年龄作为时间尺度[5-8],同时适当考虑控制出生队列的效应。但也有学者认为,以随访时间作为时间尺度、同时在模型中调整年龄是最适宜的方法[9-11]。目前文献中对于队列研究资料分析中,Cox模型的时间尺度选择问题尚未达成共识。
基于此,本研究拟对队列研究资料分析中Cox模型生存时间变量尺度选择的问题进行探讨,简述其基本原理和方法,并利用大规模人群队列研究资料举例说明不同时间尺度对分析结果的影响。同时提供几点关于时间尺度选择上的考虑和建议,以期为队列研究资料的统计分析提供参考。
一、基本原理1. Cox模型的基本原理:Cox模型通过将风险函数表达为基准风险函数和协变量函数的乘积,构建协变量与风险之间的回归关系,其基本形式:
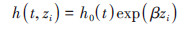 (1)
(1)
式中,风险函数h(t, zi) 表示具有协变量(组合)水平zi的个体i在t时刻发生结局事件的瞬时风险,h0(t) 为t时刻的基准风险函数,β为协变量的回归系数。
根据公式1可知,个体在某时刻发生结局事件的风险,由该时刻的基准风险以及该个体的协变量(组合)水平共同决定。公式1中基准风险函数的分布不作定义,可以为任何形式,具有非参数的特点;而协变量(组合)水平则用一个参数形式的指数函数来表达,故Cox模型是一种“半参数”回归模型。模型的参数估计可借助Cox[12]提出的偏似然函数进行:
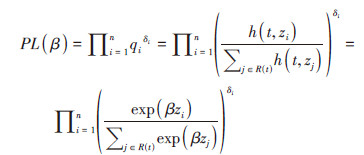 (2)
(2)
式中,qi为个体i在其随访截止时点(t时刻)的似然函数,表示个体i在t时刻发生结局事件的可能性,其分子为个体i在t时刻的风险函数,分母为t时刻处于风险状态的所有个体的风险函数之和。t时刻的可能发生结局事件的所有研究对象的集合,定义为风险集R(t),包含所有生存时间T≥t的个体。j为风险集R(t) 内的个体,其协变量(组合)水平为zj。当个体i在t时刻发生结局事件时,δi=1;当个体i在t时刻并未发生结局事件(删失)时,δi=0。
常规的似然函数应当包含全部n个样本的观测结果,但由于δi的存在,上述PL(β) 实际上只包含了结局事件时间点的似然函数,忽略了删失时点,故称之为偏似然函数[12]。公式2中分子分母的基线风险函数h0(t) 正好抵消,不对偏似然函数产生影响。根据最大似然理论,令PL(β) 达到最大值的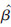
2. 不同时间尺度对Cox模型风险估计的影响:根据公式1、2可知,Cox模型中结局事件的发生时间并不直接影响偏似然函数,时间的效应包含在基准风险函数h0(t) 中,同一风险集内的所有个体都拥有相同的基准风险,在偏似然函数的分子和分母中相互抵消。实际上,不同的时间尺度正是通过影响相关风险集的构成来影响参数估计结果的。按照选定的时间尺度,所有研究对象的观测资料沿着该时间轴进行排列,在每一个结局事件发生的时间点构建似然函数,进行参数估计。
由于基准风险函数h0(t) 可以为任何形式,被选作时间尺度的变量对研究结局的效应可以得到最充分的控制。这也是Cox提出“应当选择与结局关系最密切的变量作为时间尺度”的原因[3],通过将作用最强的一个非研究因素作为时间尺度,可以最充分地控制其对暴露-结局关联的影响。如果存在多个可选的时间尺度变量,则应当将最重要的一个变量作为时间尺度,将次重要的变量放在参数部分进行调整(即纳入模型中作为协变量)[3]。
由于研究设计本身的特点,队列研究容易受到混杂偏倚的影响。在大多数情况下,年龄是暴露-疾病关联中最重要的混杂因素之一,通常需要对年龄的效应进行充分、合理的控制。因此,年龄也经常作为Cox模型中首要的候选时间尺度。在队列研究资料分析中,时间尺度的选择通常也会与年龄的调整策略同时考虑。目前文献中报道的时间尺度选择和年龄调整策略主要有4种情形。
(1)调整年龄的随访时间(FT),模型基本形式:
 (3)
(3)
式中,t为随访截止与研究开始的时间间隔,即随访时间;a0为基线年龄;zi为除年龄外的其他协变量(组合)水平;γ为年龄的回归系数。这是目前使用较为广泛的一种分析策略,相当于把所有研究对象拉到同一个观察原点,假定所有研究对象在研究开始时(t=0)的基准风险均相同。基线年龄的调整放在参数部分,可通过连续/分类变量的形式进入模型。
(2)采用研究对象的年龄(AGE1)作为时间尺度,公式:
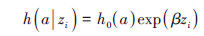 (4)
(4)
式中,a为结局事件发生的年龄。此模型假定相同年龄的个体具有相同的基准风险,但由于未考虑生存资料的左截尾信息,相当于假定研究对象从出生即开始处于风险状态,在大多数情况下并不符合科学实际。
(3)在AGE1基础上,同时考虑左截尾的年龄(AGE2)作为时间尺度,公式:
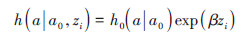 (5)
(5)
此模型假定相同年龄的个体具有相同的基准风险,同时考虑了随访资料的左截尾信息,将研究对象的发病风险区间限定在基线调查至随访截止这一范围内(a0~a),只有在a岁时已经进入研究的个体才会被纳入风险集R(a)。
(4)同样在AGE1基础上,根据出生队列分层的年龄(AGE3)作为时间尺度,公式:
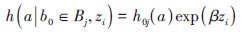 (6)
(6)
式中,b0为出生年份,Bj为出生队列j,此模型在AGE1尺度的基础上根据出生队列进行分层,在层内分别构建偏似然函数,允许基准风险函数在不同层间变化,但参数部分取值相同。
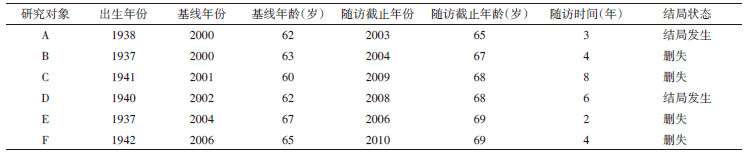
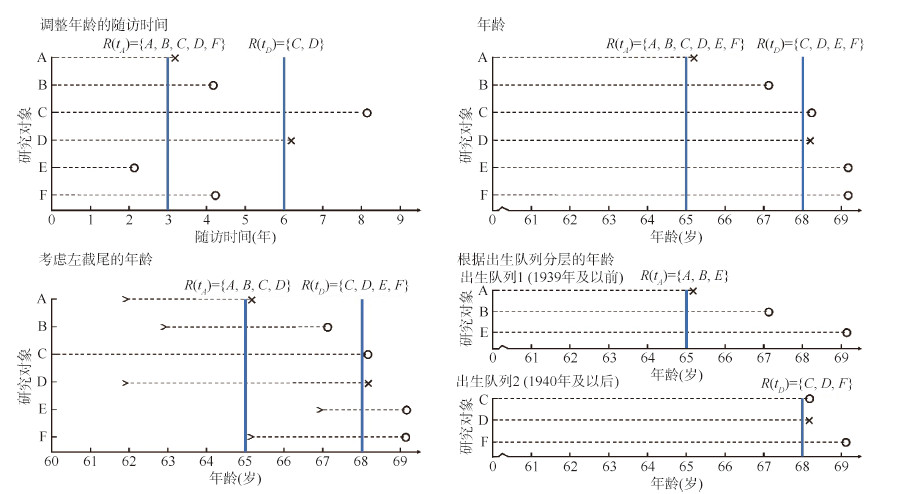
以一个虚构的包含6名研究对象的随访数据集为例,展示4种时间尺度对Cox模型风险估计的影响(表 1,图 1)。该数据集的基本情况见表 1,假设该研究从2000年开始,随访截止时间为2016年底。6位研究对象在2000-2006年内先后入组,成员A和D在研究期间发生了结局事件。图 1展示了4种时间尺度下,风险集R(tA) 和R(tD) 的构成情况。以FT尺度为例,其偏似然函数
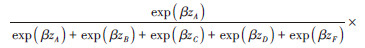
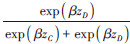
|
| 注:×:结局事件;○:删失;R(tA):tA时刻的风险集;R(tD):tD时刻的风险集 图 1 Cox模型中常用的4种时间尺度示例 |
利用上海女性健康队列资料[13],以中心性肥胖与肝癌发病风险的关联为例,比较4种时间尺度在风险估计结果上的差异。上海市肿瘤研究所流行病学研究室于1997-2000年在上海市某区建立了女性自然人群队列,研究对象为40~70岁的女性常住户籍居民,该队列的研究设计和详细实施方案见文献[13]。
本研究所关心的暴露因素为中心性肥胖,根据文献定义为腰围≥85 cm[14];结局事件定义为肝癌发病(ICD-9编码:155);随访截止时间为2016年12月31日。资料分析中共纳入72 687名研究对象,其中包含肝癌病例255例,随访时间M为18.12年。在Cox模型中分别采用4种时间尺度对中心性肥胖与肝癌发病的风险比(hazard ratio,HR)及其95%CI进行估计。除考虑年龄的作用外,模型中还额外调整了以下潜在混杂因素:文化程度(小学及以下、中学、大学及以上)、经济收入(低、中、高)、吸烟(曾经吸、从不吸)、饮酒(曾经饮、从不饮)、慢性肝炎史(有、无)、胆石症史(有、无)、肝癌家族史(有、无)、总能量摄入(kcal/d,连续变量)和总体力活动(MET-h/d,连续变量),计算结果见表 2。基于4种时间尺度估计的HR值及其95%CI分别为1.55(1.19~2.03)、1.42(1.09~1.85)、1.56(1.19~2.04)和1.53(1.17~2.00)。除AGE1尺度外,另外3种时间尺度的点估计结果和标准误均较为接近。但AGE2尺度的运算速度远远慢于其他时间尺度,在相同电脑和统计软件运行环境下所花费的时间几乎是其他时间尺度的60倍。
结合Cox模型中结局事件时间尺度的基本原理和上述研究实例,归纳4种常用时间尺度在风险函数结构、SAS代码和运算速度等方面的差异,供读者参考(表 3)。
Cox模型是流行病学研究中常用的回归模型之一,但在生存分析中结局事件的发生通常可以沿着不止一条时间轴来记录[2-3]。如本文提到的随访时间、研究对象的年龄等。在多个可选的时间度量中,由于随访时间最为直观、最易于理解,不管是干预性质的临床研究还是观察性流行病学研究中,默认采用随访时间作为Cox模型时间尺度的研究数量都远超于其他时间尺度。有时为了研究一些特殊暴露和疾病的关联,可能要选择其他时间刻度,如乳腺癌的发病时间可以记录为实际发病年龄,也可以记录为初次妊娠至发病的间隔时间,还可以记录为口服避孕药的服用年限。本研究针对Cox模型中时间刻度的选择问题展开了系统探讨,包括常用的几种时间尺度的原理、方法和区别;同时结合实例说明,并总结归纳了Cox模型中常用的几种时间尺度的特点。
1997年,Korn等[5]对观察性研究中Cox模型的时间尺度选择问题进行了探讨。并利用大规模人群纵向研究数据,分别分析了吸烟、居住地和收入水平与全因死亡风险以及卵巢切除的关联。根据研究结果,推荐使用年龄作为时间尺度,并适当考虑进行出生队列效应/时期效应的控制(类似本研究的AGE3尺度)。过去20年陆续有几项研究利用模拟数据或实际的人群随访资料探讨了此问题,其中部分研究支持以年龄作为时间尺度外加出生队列分层的分析策略[5-8, 15-16];也有研究认为,在无法确定“正确”时间尺度的情况下,随访时间是比较可靠的选择[9-11]。国内对此问题关注很少,仅2000年的一项研究利用职业锡矿工人队列资料,简单比较了两种时间尺度(分别为本研究的AGE1尺度和AGE2尺度)在识别肺癌危险因素上的区别。结果发现,使用AGE1尺度时,砷暴露表现为肺癌的保护性因素,而使用AGE2尺度的计算结果则较符合医学实际[17]。
目前大部分研究比较支持以年龄而非随访时间作为队列研究资料分析的时间尺度。首先,大部分疾病的发病风险都会随着年龄的变化而变化,把基准风险解释为“年龄的函数”,比“随访时间的函数”要更符合目前科学认知;其次,观察性流行病学研究通常需要控制年龄带来的混杂,使用随访时间作为尺度时,虽然也可以在模型中加入基线年龄作为协变量,但由于许多疾病的发病风险与年龄之间并非简单的线性关系,这种参数形式的调整往往不够充分,而将年龄当作时间尺度则可以最大程度地控制其影响(Cox模型中基准风险函数可以为任何复杂形式);最后,随访时间的长短与一些危险因素的累积暴露水平高度相关(尤其是一些职业暴露因素等),在这种情况下使用随访时间作为尺度可能会掩盖暴露因素的真实作用。
1997年Korn等[5]提出,满足以下两个条件时,使用年龄或随访时间作为Cox模型的时间尺度,可得到一致的参数估计结果。一是基准风险和年龄呈指数/近似指数关系;二是模型中的协变量与基线年龄之间相互独立。但几项模拟研究[9-11, 18]和实例研究[8-9, 18]的结果并不支持上述观点,满足以上两个条件时,随访时间和年龄尺度的分析结果也会存在差异。不同的时间尺度只有在对结局事件或删失的时间排序不同时才会导致不同的参数估计结果。不难发现,导致两种时间尺度计算结果存在差异的根本原因是研究对象基线年龄的差异,如果所有研究对象的基线年龄都相同,那么随访时间和发病年龄这两种时间尺度将是等价的。因此,当研究对象的年龄分布范围较宽或基线调查时间窗较长时,应当更加谨慎地选择Cox模型的时间尺度。此外,值得注意的是在使用发病年龄作为时间尺度时,一般都需要考虑生存资料的左截尾信息,否则相当于假定暴露从出生即开始,研究对象从出生开始即处于风险状态,对于常见环境暴露因素并不合理,因此一般不推荐直接使用AGE1尺度。对于大部分以基线情况作为暴露水平的队列研究来说,使用AGE2尺度把每个个体的风险区间限定在研究真正观测到的范围内是比较合理的;也可选用AGE3尺度,通过分层的方法对出生队列效应/时期效应进行控制。出生队列的分层方法,文献中推荐以5年作为一层较为合适[5]。
虽然几种时间尺度的含义存在明显区别,但在大多数文献报道以及本文实例分析中,HR值估计结果的差别其实并不大,尤其是FT、AGE2和AGE3尺度[5-11, 15-16, 18]。由于AGE2尺度考虑了每位研究对象的延迟进入情况,运算时间相对于其他时间尺度将耗费很多。当计算量比较大时,运算速度也可以作为时间尺度选择的一个考量因素。另外,已有研究利用模拟数据和人群随访资料进行了一系列分析,发现以随访时间作为尺度时,Cox模型的预测效果(以一致性指数来衡量)显著优于年龄尺度[9-11]。因此,如果研究目的是风险预测而非关联分析,不严格要求模型具有较好的可解释性时,可以考虑尝试不同的时间尺度以获得更好的预测效果。除了选用单一的时间变量作为Cox模型的时间尺度,还有几项研究尝试将年龄和随访时间整合在一起,构建一个“最优时间尺度”[3, 19-20]。2015年的一项研究还提出了一种新的“相对时间尺度”,基于相对生存率的思想,利用人群寿命表,根据同时期、同年龄自然人群的期望死亡风险对每个个体的随访时间进行校正,用校正后的随访时间进行风险估计[21]。但上述方法目前尚未得到广泛应用。此外,还有几项研究讨论了存在时依协变量时Cox模型的时间尺度选择问题[22-23]。
综上所述,在实际工作中如何选择时间尺度的思路可以考虑以下几条原则,如研究目的是病因探索,还是风险预测;年龄是否为所研究的暴露-疾病关联中一个重要的混杂因素;研究人群的年龄分布范围大小以及基线调查时间的跨度大小;数据计算量大小等。总之,应从研究问题出发,充分考虑研究人群的年龄构成特点以及混杂因素调整的需要等,若研究目的是风险预测,可挑选预测效果最好的模型;如果是暴露-疾病的关联分析,则应根据研究问题选择最符合科学解释的时间尺度。
利益冲突 所有作者声明无利益冲突
作者贡献声明 李卓颖:查阅文献、编写统计程序、分析数据和结果解释、撰写和修改论文;沈秋明、拓嘉怡、唐丹丹、肖宇轩、赵龙刚:参与方法学讨论和文章修改;项永兵:负责基金、课题设计和论文框架设计、参与方法学讨论和结果解释、内容修改和定稿
| [1] |
Cox DR. Regression models and life‐tables[J]. J Roy Stat Soc: Ser B (Methodol), 1972, 34(2): 187-202. DOI:10.1111/j.2517-6161.1972.tb00899.x |
| [2] |
Cox DR, Oakes D. Analysis of survival data[M]. Florida: Chapman and Hall/CRC, 2018.
|
| [3] |
Farewell VT, Cox DR. A note on multiple time scales in life testing[J]. J Roy Stat Soc: Ser C (Appl Stat), 1979, 28(1): 73-75. DOI:10.2307/2346815 |
| [4] |
Breslow NE, Lubin JH, Marek P, et al. Multiplicative models and cohort analysis[J]. J Am Stat Assoc, 1983, 78(381): 1-12. DOI:10.1080/01621459.1983.10477915 |
| [5] |
Korn EL, Graubard BI, Midthune D. Time-to-event analysis of longitudinal follow-up of a survey: choice of the time-scale[J]. Am J Epidemiol, 1997, 145(1): 72-80. DOI:10.1093/oxfordjournals.aje.a009309 |
| [6] |
Cologne J, Hsu WL, Abbott RD, et al. Proportional hazards regression in epidemiologic follow-up studies: an intuitive consideration of primary time scale[J]. Epidemiol, 2012, 23(4): 565-573. DOI:10.1097/ede.0b013e318253e418 |
| [7] |
Canchola AJ, Stewart SL, Bernstein L, et al. Cox regression using different time-scales[M]. Western Users of SAS Software. San Francisco, California, 2003.
|
| [8] |
Thiébaut AC, Bénichou J. Choice of time-scale in Cox's model analysis of epidemiologic cohort data: a simulation study[J]. Stat Med, 2004, 23(24): 3803-3820. DOI:10.1002/sim.2098 |
| [9] |
Chalise P. Time scales in epidemiological analysis[D]. The Florida State University, 2009.
|
| [10] |
Chalise P, Chicken E, McGee D. Baseline age effect on parameter estimates in Cox models[J]. J Stat Comput Sim, 2012, 82(12): 1767-1774. DOI:10.1080/00949655.2011.595010 |
| [11] |
Chalise P, Chicken E, McGee D. Performance and prediction for varying survival time scales[J]. Commun Stat-Simul C, 2013, 42(3): 636-649. DOI:10.1080/03610918.2011.650259 |
| [12] |
Cox DR. Partial likelihood[J]. Biometrika, 1975, 62: 269-276. DOI:10.1093/biomet/62.2.269 |
| [13] |
Zheng W, Chow WH, Yang G, et al. The Shanghai Women's Health Study: rationale, study design, and baseline characteristics[J]. Am J Epidemiol, 2005, 162(11): 1123-1131. DOI:10.1093/aje/kwi322 |
| [14] |
高萌, 魏玉虾, 吕筠, 等. 中国成年人代谢异常相关的体质指数和腰围切点研究[J]. 中华流行病学杂志, 2019, 40(12): 1533-1540. Gao M, Wei YX, Lyu J, et al. The cut-off points of body mass index and waist circumference for predicting metabolic risk factors in Chinese adults[J]. Chin J Epidemiol, 2019, 40(12): 1533-1540. DOI:10.3760/cma.j.issn.0254-6450.2019.12.006 |
| [15] |
Lamarca R, Alonso J, Gomez G, et al. Left-truncated data with age as time scale: an alternative for survival analysis in the elderly population[J]. J Gerontol A Biol Sci Med Sci, 1998, 53(5): M337-343. DOI:10.1093/gerona/53a.5.m337 |
| [16] |
Cheung YB, Gao F, Khoo KS. Age at diagnosis and the choice of survival analysis methods in cancer epidemiology[J]. J Clin Epidemiol, 2003, 56(1): 38-43. DOI:10.1016/s0895-4356(02)00536-x |
| [17] |
姚树祥, 巫秀美, 倪宗瓒, 等. Cox比例风险模型中生存时间变量尺度的探讨[J]. 数理医药学杂志, 2000, 13(2): 102-104. Yao SX, Wu XM, Ni ZZ, et al. An exploration of the scale of survival time variables in the Cox proportional hazard model[J]. J Math Med, 2000, 13(2): 102-104. DOI:10.3969/j.issn.1004-4337.2000.02.004 |
| [18] |
Pencina MJ, Larson MG, D'Agostino RB. Choice of time scale and its effect on significance of predictors in longitudinal studies[J]. Stat Med, 2007, 26(6): 1343-1359. DOI:10.1002/sim.2699 |
| [19] |
Duchesne T, Lawless J. Alternative time scales and failure time models[J]. Lifetime Data Anal, 2000, 6(2): 157-179. DOI:10.1023/a:1009616111968 |
| [20] |
Oakes D. Multiple time scales in survival analysis[J]. Lifetime Data Anal, 1995, 1(1): 7-18. DOI:10.1007/BF00985253 |
| [21] |
Hurley MA. A reference relative time-scale as an alternative to chronological age for cohorts with long follow-up[J]. Emerg Themes Epidemiol, 2015, 12(1): 1-12. DOI:10.1186/s12982-015-0043-6 |
| [22] |
Griffin BA, Anderson GL, Shih RA, et al. Use of alternative time scales in Cox proportional hazard models: implications for time‐varying environmental exposures[J]. Stat Med, 2012, 31(27): 3320-3327. DOI:10.1002/sim.5347 |
| [23] |
Kim M, Paik MC, Jang J, et al. Cox proportional hazards models with left truncation and time‐varying coefficient: Application of age at event as outcome in cohort studies[J]. Biom J, 2017, 59(3): 405-419. DOI:10.1002/bimj.201600003 |
 2022, Vol. 43
2022, Vol. 43