文章信息
- 黄勇, 郑志伟, 陈纯, 李科, 陈思宇, 陈远源, 景钦隆, 马钰, 罗雷, 杨智聪, 张周斌.
- Huang Yong, Zheng Zhiwei, Chen Chun, Li Ke, Chen Siyu, Chen Yuanyuan, Jing Qinlong, Ma Yu, Luo Lei, Yang Zhicong, Zhang Zhoubin
- 广州市2起由新型冠状病毒奥密克戎变异株引起的本地疫情流行病学参数研究
- Epidemiological characteristics of two local COVID-19 outbreaks caused by 2019-nCoV Omicron variant in Guangzhou, China
- 中华流行病学杂志, 2022, 43(11): 1705-1710
- Chinese Journal of Epidemiology, 2022, 43(11): 1705-1710
- http://dx.doi.org/10.3760/cma.j.cn112338-20220523-00450
-
文章历史
收稿日期: 2022-05-23
2. 广州医科大学公共卫生研究院, 广州 510440
2. Institute of Public Health, Guangzhou Medical University, Guangzhou 510440, China
2021年11月26日WHO首次报告了新型冠状病毒(新冠病毒)奥密克戎变异株,奥密克戎变异株包含若干亚分支,主要亚分支包括BA.1、BA.2、BA.3、BA.4和BA.5。自2021年12月9日我国内地报告首例奥密克戎变异株病例以来,广州、北京、上海、深圳、天津等多地均出现不同规模的奥密克戎变异株本土疫情。目前奥密克戎变异株已取代德尔塔变异株成为全球优势毒株[1]。相对于德尔塔变异株,奥密克戎变异株的潜伏期更短,传染性更强且仍在不断变异[2]。为应对奥密克戎变异株,及时动态精准地调整防控措施,持续分析其流行病学特征具有重要意义。
已有学者开展对新冠病毒流行病学参数估计的研究。Li等[3]通过指数增长法(EG)、极大似然法(ML)等5种数学模型估计2020年新冠病毒原始株基本再生数(R0)约为3.39。通过ML估计德尔塔变异株在国内的R0为3.57~4.07,传播能力明显高于原始株[4]。李亚飞等[5]发现由奥密克戎变异株(BA.1)引发的学校聚集性疫情R0为5.46。潘静静等[6]发现由奥密克戎变异株(BA.2)引发的工厂聚集性疫情的中位潜伏期为3 d,序列间隔中位数3 d,R0为6.14,但样本量偏少。提示聚集程度不同的场所可能导致R0不同。
本研究分析2022年4月8日和4月27日广州市2起新冠病毒奥密克戎变异株(BA.2)本地疫情早期的流行病学特征,根据发病病例数据估计潜伏期和序列间隔的分布,并估算R0,同时探索小型场所聚集性疫情和机场聚集性疫情对R0的影响。
资料与方法1. 基本情况:2022年4月8日和4月27日广州市发生2起新冠病毒奥密克戎变异株(BA.2)本地疫情[7-8],其中“408”疫情首例病例为3月27日发病的某服装公司员工,该起疫情以小型场所聚集性疫情为主,波及酒吧、公司等,共报告274例。“427”疫情首例病例为4月26日发病的机场员工,该起疫情以机场聚集性疫情为主,共报告148例。
2. 2起疫情广州市所采取的疫情防控措施:①“408”疫情:2022年4月8日,白云区某学校例行核酸筛查发现1例小学生核酸检测异常,广州市于4月9日发布《广州市新型冠状病毒肺炎疫情防控指挥部通告(第32号)》并迅速启动全市11个区第一轮全员核酸筛查,其中将白云区除封控区和管控区外的其他区域划定为防范区[7, 9]。4月10日,全市中小学(有住宿条件和全封闭管理条件的高三年级除外)暂停线下教学,采取线上教学[10]。4月12日,全市启动第二轮全员核酸筛查[11]。4月20日起,全市幼儿园及中小学(白云区除外)有序恢复线下教学[12]。②“427”疫情:4月27日,因白云区白云机场例行核酸采样中发现机场工作人员核酸检测异常,4月28-29日全市11个区开展第三轮全员核酸筛查,并对白云机场进行有效管控[8, 13]。4月30日,实现社会面清零[14]。5月4日,全市实施第四轮全员核酸筛查。5月7日,全市实施第五轮全员核酸筛查。5月13日,白云机场恢复常态化运行[15]。
3. 数据来源:病例信息来源于2022年4月8日至5月8日中国疾病预防控制信息系统中广州市所有新冠病毒肺炎本土病例传染病报告卡信息和个案流行病学调查。
4. 潜伏期估计:潜伏期指在新冠病毒侵入机体到最早出现临床症状或体征的时间之差[16],是确定密切接触者隔离期限和判断病例感染时间的重要依据。计算潜伏期需确定新冠病毒肺炎感染者的暴露时间和发病时间。对于暴露时间,对传播链清晰且流行病学调查资料准确的个案病例进行疾病潜伏期估计最佳。因此,本研究选取有明确、唯一暴露源且仅暴露一次的病例进行分析,并采用Weibull、Gamma和lognormal概率密度分布模型拟合相关数据。采用Akaike信息准则(Akaike information criterion,AIC)进行定量分析,其中AIC值越小,说明模型拟合程度越高[17]。确定最优分布后,再利用Bootstrap方法进行10 000次重抽样计算中位数及其95%CI。
5. 序列间隔估计:序列间隔指一个感染者发病时间与其下一代感染者发病时间之差[16]。代表疾病从一个人传至另一个人的平均间隔时间。值越小,疫情越容易呈现暴发模式。参数估计方法同潜伏期。
6. R0及实时再生数(Rt)估计:①R0:在没有干预的情况下,即政府实施防控措施前,一个病例造成的新发病例数的平均数量[18-19],对于评估病毒传播能力和提示疫情起始规模具有重要意义。②Rt:当政府采取防控措施后,病毒的传播能力受到限制,此时疫情的传播速度可用Rt表示,即在t时刻一个病例造成的新发病例数的平均数量[18-19]。Rt会随时间动态变化,主要用于评估疫情的进展和防控措施的有效程度,当Rt保持在1以下,说明该防控措施下疫情将得到控制[19]。③估计方法:在获得序列间隔的最优分布及该分布参数的基础上,结合政府实施分级防控前的发病病例数,分别采用EG和ML估计R0[3],并用决定系数(R2)和均方根误差(root mean squared error,RMSE)评估模型拟合程度。R2越大,RMSE越小,模型拟合程度越高[16]。利用序列间隔的均值、标准差和每日发病病例数计算Rt,因每天Rt波动较大,参数上设置平滑7 d对其进行滚动计算。采用R软件工具包R0和EpiEstim分别计算R0和Rt。
7. 统计学方法:上述分析应用R 4.0.2软件完成。因潜伏期和序列间隔不服从正态分布,计量资料以M(Q1,Q3)表示。采用非参数检验法比较2起疫情在潜伏期、序列间隔的差异。基于重抽样法估计的中位数和95%CI对比2起场所聚集程度不同的疫情在R0上的差异。检验水准α=0.05。
结果1. 基本情况:2022年4月8日至5月8日广州市共报告新冠病毒奥密克戎变异株(BA.2)感染者422例,其中感染来源明确且仅暴露一次的感染者共79例。其中“408”小型场所聚集性疫情61例(77.2%),“427”机场聚集性疫情18例(22.8%)。
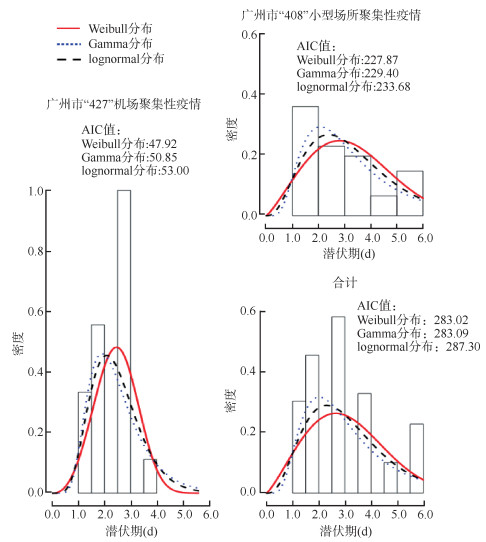
2. 潜伏期估计:新冠病毒奥密克戎变异株(BA.2)潜伏期范围为1.00~6.00 d,M(Q1,Q3)为3.00(2.00,4.00)d,平均值为3.07 d。基于三种分布的概率密度分布见图 1和表 1。三种分布中,潜伏期的估计以Weibull分布对应的AIC值最小,经Bootstrap进行10 000次重抽样的M(95%CI)为2.94(2.52~3.38)d。其中,“427”机场聚集性疫情的潜伏期[M(95%CI)为2.44(1.99~2.91)d]与“408”小型场所聚集性疫情差异尚不显著[M(95%CI)为3.12(2.62~3.67)d],P=0.064。
|
| 图 1 2022年广州市2起疫情新型冠状病毒奥密克戎变异株(BA.2)潜伏期频率分布 |
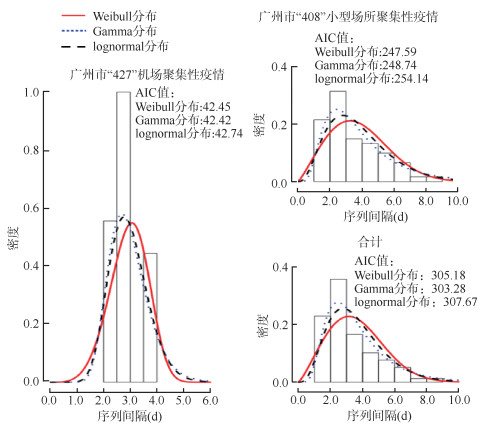
3. 序列间隔估计:新冠病毒奥密克戎变异株(BA.2)序列间隔范围为1.00~9.00 d,M(Q1,Q3)为3.00(3.00,4.50)d,平均值为3.62 d。基于三种分布的概率密度分布见图 2和表 1。三种分布中,序列间隔的估计以Gamma分布对应的AIC值最小。经Boostrap进行10 000次重抽样的M(95%CI)为3.32(2.89~3.81)d。其中,“427”机场聚集性疫情的序列间隔[M(95%CI)为2.90(2.52~3.30)d]与“408”小型场所聚集性疫情差异尚不显著[M(95%CI)为3.65(3.09~4.28)d],P=0.071。
|
| 图 2 2022年广州市2起疫情新型冠状病毒奥密克戎变异株(BA.2)序列间隔频率分布 |
4. R0及Rt估计:根据广州市实施分级防控前的发病病例数和序列间隔估计值,在“408”小型场所聚集性疫情中,ML计算得R0为3.76(95%CI:3.31~4.22),R2=67%,RMSE=2.10;EG计算得R0为4.40(95%CI:3.95~4.85),R2=71%,RMSE=1.21。鉴于EG的R2高于ML(71% vs. 67%),且RMSE小于ML(1.21 vs. 2.10),因此,EG的拟合效果最优。
在“427”机场聚集性疫情中,ML计算得R0为6.77(95%CI:6.45~7.10),R2=69%,RMSE=15.26;EG计算得R0为11.35(95%CI:11.02~11.67),R2=71%,RMSE=13.04。鉴于EG的R2高于ML(71% vs. 69%),且RMSE小于ML(13.04 vs. 15.26),因此,EG的拟合效果最优。
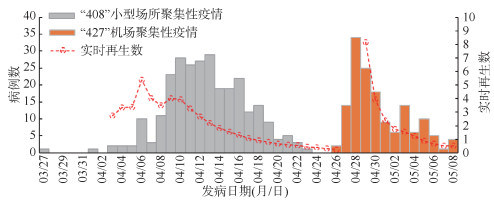
“427”机场聚集性疫情的R0为11.35(95%CI:11.02~11.67)远高于“408”小型场所聚集性疫情(R0=4.40,95%CI:3.95~4.85),且“408”小型场所聚集性疫情的Rt先缓慢升高再缓慢下降,而“427”机场聚集性疫情Rt先急剧升至高峰,再快速下降。见图 3。
|
| 图 3 2022年广州市2起疫情发病流行曲线和实时再生数趋势图 |
2022年4-5月我国广州市2起奥密克戎变异株(BA.2)疫情的中位潜伏期为2.94 d,与2021年12月挪威奥密克戎变异株疫情、2022年我国河南省奥密克戎变异株疫情估计的潜伏期3 d相近[6, 20],但短于2021年5月我国广州市德尔塔变异株疫情估计的潜伏期4.7 d[21],也短于2020年我国武汉市原始株疫情估算的潜伏期5.2 d[22]。本研究2起疫情的潜伏期的最优分布均为Weibull分布,与Backer等[23]结果一致,但也有部分学者发现Gamma分布和lognormal分布为潜伏期最优分布[24-25],可能原因为三种分布类型近似[25]。潜伏期与留验、检疫和医学观察时限密切相关,潜伏期越短,一方面提示需要加快疫情防控工作的响应速度,另一方面提示可以适当缩短密切接触者和次密切接触者的隔离期。
我国广州市2起奥密克戎变异株(BA.2)疫情的中位序列间隔为3.32 d,与2022年我国河南省奥密克戎变异株疫情的3 d、2022年韩国奥密克戎变异株疫情的3.78 d相近[6, 26],与2021年5月我国广州市德尔塔变异株疫情估计的序列间隔3 d、2021年韩国德尔塔疫情的3.6 d相近[21, 27],但短于2020年原始株的7.5 d[22]。本研究2起疫情序列间隔的最优分布分别为Weibull分布和Gamma分布,而总体最优分布为Gamma分布,与Talmoudi等[28]结果一致,但也有部分学者发现Weibull分布和lognormal分布为序列间隔最优分布[29-30]。这种不一致与三种分布类型近似、样本量等因素相关[25]。
即使是同一变异株,在人员聚集程度不同的场所下也有所不同[31]。本研究发现,由奥密克戎变异株(BA.2)引起的以酒吧、公司等小型场所聚集为主的疫情的R0为4.40,小于由奥密克戎变异株(BA.1)引起的以学校聚集性为主的疫情(R0=5.46)[5],小于由奥密克戎变异株(BA.2)引起的以工厂聚集性为主的疫情(R0=6.14)[6],小于本研究由奥密克戎变异株(BA.2)引起的以机场聚集性为主的疫情(R0=11.35)。提示场所聚集程度越高,R0越大,越需要以更快的速度和更果断的措施切断传播链,否则极易引起更大规模的本地疫情暴发和大范围的外溢。除了场所聚集程度,口罩使用率、疫苗覆盖度等也可能会影响R0和疫情传播。本研究2起疫情的R0分别为4.40和11.35,高于2020年原始株的2.2[22]和2021年广州市德尔塔疫情的3.2[21]。在估计方法上,2起疫情的最优拟合方法均为EG,与多数学者使用的估计方法一致[18, 32]。
因出现疫情后政府会迅速实施防控措施,Rt的趋势通常先上升后下降。本研究中,“408”小型场所聚集性疫情的Rt趋势为先升后降,与2022年河南省工厂聚集性疫情和学校疫情的Rt趋势一致[5-6],也与2021年广州市德尔塔疫情的Rt趋势一致[21]。而“427”机场聚集性疫情的Rt趋势直接为升至高峰后快速下降,这可能与其高度聚集、例行核酸策略和人员快速管控有关。机场工作人员例行核酸策略便于早期在高风险人群中发现感染源,机场工作人员及旅客快速管控有助于减少外溢。
本研究选择有明确唯一的暴露源且仅暴露一次的病例数据估计潜伏期和序列间隔,获得的结果会比基于报告病例数统计的要精确。不足之处在于机场聚集性疫情的样本量较小,仅18例,主要原因在于机场内人员流动频繁,员工交流密切,且多数共用食堂等公共场所,导致多数病例有持续暴露史或无明确感染来源。
综上所述,本研究提供了奥密克戎变异株(BA.2)的流行病学特征,阐述了不同聚集性场所对R0的影响,尤其是机场聚集性疫情,为进一步的疫情分析提供了重要参数,同时也为实时动态调整防控措施提供科学依据。
利益冲突 所有作者声明无利益冲突
作者贡献声明 黄勇、郑志伟:研究设计、数据收集及整理、论文撰写、论文修改;陈纯、李科、陈思宇、陈远源:实施研究、采集数据、论文修改和指导;景钦隆、马钰、罗雷、杨智聪:研究设计、论文指导、技术支持;张周斌:研究设计、论文修改/指导、经费支持、技术支持
| [1] |
WHO. Weekly epidemiological update on COVID-19[EB/OL]. (2022-02-22)[2022-06-23]. https://www.who.int/publications/m/item/weekly-epidemiological-update-on-covid-19-22-february-2022.
|
| [2] |
Saxena SK, Kumar S, Ansari S, et al. Characterization of the novel SARS-CoV-2 Omicron (B. 1.1. 529) variant of concern and its global perspective[J]. J Med Virol, 2022, 94(4): 1738-1744. DOI:10.1002/jmv.27524 |
| [3] |
Li JH, Wang YJ, Gilmour S, et al. Estimation of the epidemic properties of the 2019 novel coronavirus: a mathematical modeling study[Z]. medRxiv, 2020. DOI: 10.1101/2020.02.18.20024315.
|
| [4] |
王廉皓, 张翔宇, 王雪纯, 等. 中国新型冠状病毒德尔塔突变株传播强度分析[J]. 现代预防医学, 2022, 49(7): 1165-1169. Wang LH, Zhang XY, Wang XC, et al. Transmission intensity analysis of SARS-Cov-2 delta mutant in China[J]. Mod Prev Med, 2022, 49(7): 1165-1169. |
| [5] |
李亚飞, 范威, 王文华, 等. 一起由新冠病毒奥密克戎变异株引起的学校聚集性疫情[J]. 中国公共卫生, 2022, 38(5): 614-618. Li YF, Fan W, Wang WH, et al. A school cluster outbreak of COVID-19 caused by SARS-COV-2 omicron variant[J]. Chin J Public Health, 2022, 38(5): 614-618. DOI:10.11847/zgggws1138512 |
| [6] |
潘静静, 王莹莹, 王文华, 等. 一起由奥密克戎变异株BA. 2.2引起的河南省新冠肺炎本土疫情流行病学特征分析[J]. 中国公共卫生, 2022, 38(5): 1-5. Pan JJ, Wang YY, Wang WH, et al. Epidemiological characteristics of a local COVID-19 outbreak caused by Omicron (BA. 2.2) variant in Henan province[J]. Chin J Public Health, 2022, 38(5): 1-5. DOI:10.11847/zgggws1138726 |
| [7] |
广州市人民政府. 2022年4月9日广州市疫情防控新闻发布会[EB/OL]. (2022-04-09)[2022-06-09]. http://www.gz.gov.cn/xw/xwfbh/content/post_8176897.html.
|
| [8] |
广州市人民政府. 2022年4月29日广州市疫情防控新闻发布会[EB/OL]. (2022-04-29)[2022-06-09]. http://www.gznews.gov.cn/167310.shtml.
|
| [9] |
广州市新型冠状病毒肺炎疫情防控指挥部. 广州市新型冠状病毒肺炎疫情防控指挥部通告(第32号)[EB/OL]. (2022-04-09)[2022-06-09]. http://www.gz.gov.cn/xw/tzgg/content/post_8176408.html.
|
| [10] |
广州市教育局. 广州市新型冠状病毒肺炎疫情防控指挥部办公室教育疫情防控工作专班关于各级各类学校教学安排的通告[EB/OL]. (2022-04-11)[2022-06-09]. http://www.gz.gov.cn/xw/tzgg/content/post_8178920.html.
|
| [11] |
排骨. 2022年4月12日广州11区开展全员核酸检测[EB/OL]. (2022-04-12)[2022-06-09]. http://gz.bendibao.com/news/2022412/312915.shtm.
|
| [12] |
广州市人民政府. 4月20日起广州全市中学(白云区除外)返校复课[EB/OL]. (2022-04-18)[2022-06-09]. http://m.gz.bendibao.com/mip/313440.html.
|
| [13] |
广州白云国际机场. 白云机场从即日起调整部分国内客运航班计划[EB/OL]. (2022-04-28)[2022-06-09]. https://www.gbiac.net/byairport-web/menu/index?urlKey=news&id=7065.
|
| [14] |
海阔天空. 4月30日以来广州已连续6天实现社会面清零[EB/OL]. (2022-05-05)[2022-06-09]. http://gz.bendibao.com/news/202255/content314674.shtml.
|
| [15] |
广州白云国际机场. 2022年5月13日白云机场恢复常态化运行[EB/OL]. (2022-05-13)[2022-06-09]. https://www.gbiac.net/byairport-web/menu/index?urlKey=news&id=7092.
|
| [16] |
宋倩倩, 赵涵, 方立群, 等. 新型冠状病毒肺炎的早期传染病流行病学参数估计研究[J]. 中华流行病学杂志, 2020, 41(4): 461-465. Song QQ, Zhao H, Fang LQ, et al. Study on assessing early epidemiological parameters of COVID-19 epidemic in China[J]. Chin J Epidemiol, 2020, 41(4): 461-465. DOI:10.3760/cma.j.cn112338-20200205-00069 |
| [17] |
Cauchemez S, Fraser C, van Kerkhove MD, et al. Middle East respiratory syndrome coronavirus: quantification of the extent of the epidemic, surveillance biases, and transmissibility[J]. Lancet Infect Dis, 2014, 14(1): 50-56. DOI:10.1016/S1473-3099(13)70304-9 |
| [18] |
王莹, 尤心怡, 王奕婧, 等. 中国新型冠状病毒肺炎疫情基本再生数评估[J]. 中华流行病学杂志, 2020, 41(4): 476-479. Wang Y, You XY, Wang YJ, et al. Estimating the basic reproduction number of COVID-19 in Wuhan, China[J]. Chin J Epidemiol, 2020, 41(4): 476-479. DOI:10.3760/cma.j.cn112338-20200210-00086 |
| [19] |
韩珂, 贾王平, 曹文哲, 等. 一线城市新型冠状病毒肺炎实时基本再生数估算及流行现状评估[J]. 解放军医学院学报, 2020, 41(4): 421-425, 429. Han K, Jia WP, Cao WZ, et al. Estimation of real-time basic reproduction number and epidemic status of 2019 novel coronavirus diseases (COVID-19) in first-tier cities[J]. Acad J Chin PLA Med Sch, 2020, 41(4): 421-425, 429. DOI:10.3969/j.issn.2095-5227.2020.04.023 |
| [20] |
Brandal LT, Macdonald E, Veneti L, et al. Outbreak caused by the SARS-CoV-2 Omicron variant in Norway, November to December 2021[J]. Euro Surveill, 2021, 26(50): 2101147. DOI:10.2807/1560-7917.ES.2021.26.50.2101147 |
| [21] |
Zhang M, Xiao JP, Deng AP, et al. Transmission dynamics of an outbreak of the COVID-19 delta variant B. 1.617. 2-Guangdong province, China, May-June 2021[J]. China CDC Wkly, 2021, 3(27): 584-586. DOI:10.46234/ccdcw2021.148 |
| [22] |
Li Q, Guan XH, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia[J]. N Engl J Med, 2020, 382(13): 1199-1207. DOI:10.1056/NEJMoa2001316 |
| [23] |
Backer JA, Klinkenberg D, Wallinga J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 January 2020[J]. Euro Surveill, 2020, 25(5): 2000062. DOI:10.2807/1560-7917.ES.2020.25.5.2000062 |
| [24] |
李盈科, 赵时, 楼一均, 等. 新型冠状病毒肺炎的流行病学参数与模型[J]. 物理学报, 2020, 69(9): 090202. Li YK, Zhao S, Lou YJ, et al. Epidemiological parameters and models of coronavirus disease 2019[J]. Acta Phys Sin, 2020, 69(9): 090202. DOI:10.7498/aps.69.20200389 |
| [25] |
杜志成, 顾菁, 李菁华, 等. 基于区间删失数据估计方法的COVID-19潜伏期分布估计[J]. 中华流行病学杂志, 2020, 41(7): 1000-1003. Du ZC, Gu J, Li JH, et al. Estimating the distribution of COVID-19 incubation period by interval-censored data estimation method[J]. Chin J Epidemiol, 2020, 41(7): 1000-1003. DOI:10.3760/cma.j.cn112338-20200313-00331 |
| [26] |
Kim D, Ali ST, Kim S, et al. Estimation of serial interval and reproduction number to quantify the transmissibility of SARS-CoV-2 omicron variant in South Korea[J]. Viruses, 2022, 14(3): 533. DOI:10.3390/v14030533 |
| [27] |
Ryu S, Kim D, Lim JS, et al. Serial interval and transmission dynamics during SARS-CoV-2 delta variant predominance, South Korea[J]. Emerg Infect Dis, 2022, 28(2): 407-410. DOI:10.3201/eid2802.211774 |
| [28] |
Talmoudi K, Safer M, Letaief H, et al. Estimating transmission dynamics and serial interval of the first wave of COVID-19 infections under different control measures: a statistical analysis in Tunisia from February 29 to May 5, 2020[J]. BMC Infect Dis, 2020, 20(1): 914. DOI:10.1186/S12879-020-05577-4 |
| [29] |
Kwok KO, Wong VWY, Wei WI, et al. Epidemiological characteristics of the first 53 laboratory-confirmed cases of COVID-19 epidemic in Hong Kong, 13 February 2020[J]. Euro Surveill, 2020, 25(16): 2000155. DOI:10.2807/1560-7917.ES.2020.25.16.2000155 |
| [30] |
Ratovoson R, Razafimahatratra R, Randriamanantsoa L, et al. Household transmission of COVID-19 among the earliest cases in Antananarivo, Madagascar[J]. Influenza Other Respir Viruses, 2022, 16(1): 48-55. DOI:10.1111/irv.12896 |
| [31] |
黄丽红, 沈思鹏, 余平, 等. 基于动态基本再生数的新型冠状病毒肺炎疫情防控现状评估[J]. 中华流行病学杂志, 2020, 41(4): 466-469. Huang LH, Shen SP, Yu P, et al. Dynamic basic reproduction number based evaluation for current prevention and control of COVID-19 outbreak in China[J]. Chin J Epidemiol, 2020, 41(4): 466-469. DOI:10.3760/cma.j.cn112338-20200209-00080 |
| [32] |
Yu CJ, Wang ZX, Xu Y, et al. Assessment of basic reproductive number for COVID-19 at global level: a meta-analysis[J]. Medicine, 2021, 100(18): e25837. DOI:10.1097/MD.0000000000025837 |
 2022, Vol. 43
2022, Vol. 43