文章信息
- 刘杰, 汤后林.
- Liu Jie, Tang Houlin
- 模糊层次分析法在医学相关领域风险评估中的应用
- Application of fuzzy analytic hierarchy process in risk assessment in medicine related fields
- 中华流行病学杂志, 2022, 43(5): 766-770
- Chinese Journal of Epidemiology, 2022, 43(5): 766-770
- http://dx.doi.org/10.3760/cma.j.cn112338-20211130-00935
-
文章历史
收稿日期: 2021-11-30
风险评估是对某一现象带来的损失程度进行量化,包括风险识别、风险分析和风险评价[1]。医学相关领域(如医疗设施、医学决策、临床用药等)涉及许多难以清楚界定和精准量化的模糊现象[2],此类模糊现象存在不确定性,对其进行风险评估时,为量化风险,需采用针对不确定性模糊现象的方法进行风险评估。本文通过模糊层次分析法(fuzzy analytic hierarchy process,FAHP),从其基本思想、基本步骤、应用优势及其在医学相关领域风险评估的应用现状进行综述。
一、FAHP的基本思想[2]FAHP根据待评价目标,将涉及到的众多复杂因素和因素之间的复杂关系整理为自上而下的多层次阶梯状模型,以上层元素为准则进行同层元素两两比较,确定因素相对重要程度,建立模糊判断矩阵,从而分层次进行模糊综合评价。FAHP不仅可将界限不清、不易定量的因素定量化,简化分析和计算的过程,还可将主观评价过程系统化,尤其适合于人的定性判断起重要作用、决策结果难以直接量化的场合,可以很好地解决评价过程中判断的模糊性和不确定性,为不确定风险的综合评价问题提供评价方法。
二、FAHP的基本步骤[2]1. 构造指标层次:目标层:使用该方法要达到的终目标;准则层:实现预期目标所涉及的相关一级指标;指标层:实现预期目标所涉及的相关二级指标。
2. 构造判断集:各层元素两两比较,由熟悉该研究问题的专家根据0.1~0.9标度法构造判断集fij,其中fij表示因素i与因素j相比,对于目标的重要程度,fji=1-fij(i,f=1,2,…,n)[3]。
3. 构造模糊一致判断矩阵A':
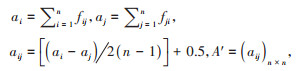
模糊一致判断矩阵的表示形式:
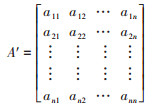
4. 计算矩阵最大特征根和权重向量:利用统计软件,如MATLAB计算矩阵的权重向量Wi,得到权重向量集W=(W1,W2,...,Wn)。
5. 构造评价矩阵:设因素集U=(u1,u2,…,um),即准则层所涉及到的所有m个因素,评价集V={v1,v2,…,vn},即每一因素所属的n个评价等级(一般设3~5个评价等级)。判断ui在评价级vi(i=1,2,…,n)的隶属度,记为rij,即认为元素ui处于评价级vi的专家数占所有评价专家的总数。汇总m个因素的单因素评价集构成总评价矩阵R:
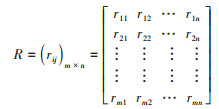
6. 进行模糊合成并做出决策:利用权重向量集W和总评价矩阵R进行模糊合成,得到被评价事物总体上对各评价等级的隶属程度。
设决策集B=(b1,b2,…,bn),令B=W·R(·为算子符号),bj表示被评价对象具有评语vj的程度,可根据最大隶属度原则[2],选择最大的bj所对应的等级vj作为最终综合评价的结果。
三、FAHP的应用优势[2]常用的综合评价方法很多,除了本文综述的FAHP外,还有数据包络分析法、人工神经网络评价法以及灰色综合评价法等。FAHP作为一种定性、定量相结合的综合评价方法,当结果涉及模糊概念甚至与评价者经验有关时,通过构建层次结构,将元素分层比较,使决策过程数字化,不仅能将复杂的定性结果定量分析,而且可以很好地解决评价过程中判断的模糊性和不确定性,所需样本数据少、数据类型简单、决策花费时间短,因此在决策和管理方面得到很好的应用。该方法关于隶属函数的确定和模糊合成算法方面有待于进一步完善。而数据包络分析法虽基于各指标的客观数据进行评价,可消除人为因素引起的误差,但各个决策部分缺乏可比性。人工神经网络评价法虽可降低人为因素的影响,但每一指标最后的权重值并无实际比较意义,且需要大量既往样本获得经验值。灰色综合评价法虽是一种定性、定量相结合的评价方法,但应用时要求所分析数据具有时间序列的特性。
四、FAHP在医学相关领域风险评估中的应用FAHP最初多用于工业领域建筑施工风险评估[3],随着该方法的日渐成熟,经济[4]、环境[5]等领域也常用该方法进行风险评估。随着其应用范围的扩大,FAHP逐渐被应用至医学相关领域,从基础医疗设施、日常医学决策、合理用药等方面到众多影响疾病的不确定性因素和错综复杂的中间环节等。这些领域所涉及的风险因素包括定性和定量因素,而诸如“设施规模”“病情急缓”“传播风险”等指标大多带有模糊性,在对所涉风险进行综合评价时,该领域专家的工作经验和判断能力也会对风险评估起到重要影响,此时运用FAHP不仅可以将定性分析和定量分析有效结合,还可充分利用专家经验为多层次决策问题提供决策支撑,事先对可能的风险因素进行综合评价从而规避风险,有助于决策者正确做出决策。
1. 在医疗设施风险评估中的应用:医院在进行建造选址和科室布局方面所涉及的自然、社会因素广泛,中间环节众多,由此带来的相关风险难以完全量化评估。Tripathi等[6]为评价适宜的医院选建地址,通过文献回顾、结合专家意见,共确定了3个一级指标和11个二级指标,通过建立指标层次,对同级指标两两比较,根据相应标度确定指标权重,建立模糊一致判断矩阵,综合地理信息系统和FAHP结果生成适宜选址图,最终确定医院最优建址。Lin和Wang[7]为研究手术室最优布局,从硬件、环境等4个方面,综合8个指标建立指标体系,采用FAHP确定各指标权重,经模糊评价对待选设计方案进行评价,从而选定手术室最优布局方案。
2. 在医学决策风险评估中的应用:医学决策离不开决策者工作经验影响,决策过程伴随主观定性因素,常需对定性因素进行决策分析。采用FAHP可通过建立模糊一致判断矩阵,将定性因素定量分析,有助于决策者做出最佳决策。例如为了确定小儿包皮环切手术的首选麻醉方法,Hancerliogullari等[8]通过文献综述和专家建议,拟定4个一级标准、8个二级标准和3个备选方案,邀请3位该领域专家对同级待评估标准进行比较打分,采用FAHP赋予各级标准权重,结果显示麻醉的时间因素是选择手术方案最重要的参考标准,经模糊合成后显示,首选麻醉方案为全身麻醉伴阴茎阻滞。为帮助决策者在新型冠状病毒肺炎(COVID-19)大流行期间选择最佳干预策略,Samanlioglu和Kaya[9]运用FAHP方法选择不同科室7名医生对世界各国在COVID-19大流行期间采用的15种干预策略进行两两比较,利用标度法赋予权重并以权重值进行排序,结果显示,紧急情况及时告知是COVID-19大流行期间的最佳防控策略,隔离患者和疑似感染者策略次之。
3. 在用药风险评估中的应用:临床用药经历制药、运输等多个中间环节,用药时需考虑患者自身和外部等多种因素影响,只有正确评估中间环节风险,根据患者情况准确用药才能达到安全用药的目的。影响中药制剂制造成本的因素众多且由于制剂存在隐形价值,导致制药成本核算困难、制剂定价困难。蔡娟娟等[10]通过调查南京市某医院中药制剂,运用FAHP及灰色关联分析法建立定价指标体系,利用该体系对肺宁合剂定价方案进行验证研究,结果表明基于FAHP的中药制剂定价与实际定价一致,该体系对中药制剂价格制定具有参考价值。马莹和褚淑贞[11]研究药品配送风险,利用FAHP从进货风险、储存风险等5个风险层面深入分析配送环节的各个过程,建立药品配送风险评价指标体系,以某医院为例验证该评价体系可行性,结果显示,其药品配送风险与该医院实际药品配送风险基本一致。
4. 在疾病预防风险评估中的应用:
(1)在传染病风险评估中的应用:传染病的传染源、传播途径多样,中间环节错综复杂,加剧了传染病传播风险的不确定性。既往传染病传播风险评估常用传染病疫情报告系统进行描述流行病学分析[12];或采集数据,结合历史疫情,分析传播风险因素[13];也有学者利用非齐次Hawkes模型进行传染病实时预测[14]。但以上方法无法规避传染病传播过程中所涉及的难以定量的模糊因素。Li等[15]应用FAHP研究广东省寨卡病毒的传播风险,通过文献回顾和专家咨询,共收集5类15个风险评估指标,邀请14位专家根据0.1~0.9标度法确定指标权重,建立指标层次,并进行模糊综合评价,结果显示蚊虫密度是影响寨卡病毒传播风险的最重要因素,且该病毒夏、秋季传播风险高于冬、春季。为评估绍兴市新发传染病暴发或流行风险,Tu等[16]选择21种新发传染病,邀请41名临床专家从传染源、传播途径及预防控制措施3个方面,选择14个影响因素构建指标体系,赋予各指标权重并建立模糊一致判断矩阵进行模糊合成,结果显示艾滋病是绍兴市最危险的新发传染病。蓝泳铄和宋世斌[17]评估高致病性禽流感的发生风险,通过FAHP确定影响禽流感各风险因素权重,用多指标综合评分法计算出风险概率并建立风险模型,成功应用于2008年春季我国各省份禽流感疫情风险评估。
(2)在慢性病风险评估中的应用:慢性病的危险因素众多,因素之间的相互作用错综复杂,且许多危险因素尚未查明,导致慢性病患病风险难以评估。Sabahi[18]利用双峰FAHP对冠心病危险因素进行评估,选择法国某医院152例冠心病患者,收集可能的风险因素建立指标体系,运用FAHP将指标体系进行模糊运算,构建评价模型,结果表明,使用该方法预测患者冠心病患病风险的准确率高达85%以上。李霞等[19]应用FAHP对51例高血压患者和39例血压正常者的4个生理参数分别进行比较并建立层次结构,对两组人群心血管健康状况进行模糊评估,结果显示血压正常者的评估得分高于高血压患者,该模型评估结果与两组t检验结果一致。
(3)在职业卫生风险评估中的应用:从业人员所面临的职业风险因素众多,其中工作环境质量、精神压力等因素难以定量分析,导致其所面临的职业风险难以正确评估,职业病屡见不鲜。为研究护士和院前急救人员的职业压力,Rajabi等[20]通过问卷和文献综述等方法收集该人群压力因素,由30名专家选择主要因素根据FAHP建立指标层次并进行模糊运算,结果显示,影响该人群职业压力的主要因素是医院管理因素和患者护理因素。隐孢子虫实验的各环节都存在不确定的安全隐患,熊彦红等[21]通过问卷调查和专家咨询采集风险因素,通过FAHP构建模糊综合评价模型,利用该模型对隐孢子虫实验室检测的风险因素进行分析,结果显示,实验室中隐孢子虫粪便样本处理属于高危风险因素。Honarbakhsh等[22]研究医护人员拒绝使用N95口罩的影响因素,通过横断面调查,将6个因素纳入研究并建立指标体系,按FAHP步骤构建评价模型,结果显示,面部发热、呼吸困难、交流困难是医护人员拒绝使用N95口罩的主要风险因素。
四、小结FAHP在医学相关领域多用于医疗设施、医学决策和用药风险评估等,通过对相关风险因素进行重要性判别,可提前规避高风险因素,有助于选择最优设施,做出最佳决策,安全合理用药;在职业卫生相关风险评估中,识别作业场所影响工人健康的高风险因素,有助于改进作业场所工作环境,提高工人健康水平。FAHP在慢性病和传染病相关风险研究中应用较少,应用该方法可将疾病风险评估涉及的多病因、多环节,从分子水平乃至社会经济水平都建立于同一指标体系,也可将依靠评判者主观经验的评价结果和难以定量的复杂因素定量分析。例如慢性病影响因素众多,且大多是模糊因素,不能确定其致病风险,有些因素甚至只是影响患病的中间环节,或者由于该因素的存在增加患病风险,FAHP针对此类风险因素建立指标体系,确定指标之间相对风险权重值,通过建立评价集,与风险指标体系进行模糊合成,达到对不同风险因素的综合评价,进而确定患病风险。在传染病中,由于传染源、传播途径涉及到的自然、社会因素多而复杂,易感人群界限模糊,在对传染性疾病的传播风险进行评估时,利用FAHP可将传染病所涉及的复杂模糊因素构建出清晰的风险指标层次结构,将某些定性因素转为定量分析,使研究过程逻辑化,研究结果清晰化、数字化。
艾滋病作为一种慢性传染病,具备慢性和传染性疾病的共同特征,其感染风险因素众多,因素之间关系复杂。MSM感染风险[23]、感染者家庭内传播风险[24-25]等研究在进行感染风险筛查时可从性行为特征、安全套使用情况、抗病毒治疗情况、家庭支持情况等多角度建立风险指标体系,利用FAHP确定各因素影响程度,建立感染风险评估模型,最终量化研究对象感染风险并进行综合评价。
目前,FAHP在艾滋病领域的风险评估研究较少,合理使用该方法进行风险评估有助于科学有效地找到艾滋病流行和传播的关键因素,判断相关风险程度,从而为目标人群做出最优决策,合理分配有限的卫生资源,达到精准干预的目的。
利益冲突 所有作者声明无利益冲突
作者贡献声明 刘杰:论文撰写、文献资料收集;汤后林:研究指导、论文修改、经费支持
| [1] |
朱军. 风险评估[M]. 北京: 经济管理出版社, 2020. Zhu J. Risk assessment[M]. Beijing: Economy & Management Publishing House, 2020. |
| [2] |
杜栋, 庞庆华, 吴炎. 现代综合评价方法与案例精选[M]. 3版. 北京: 清华大学出版社, 2015. Du D, Pang QH, Wu Y. Modern comprehensive evaluation method and case selection[M]. 3rd ed. Beijing: Tsinghua University Press, 2015. |
| [3] |
钱辉, 杨森, 彭琪琪, 等. 基于模糊层次分析法对高电压下耐压测试系统的风险评估[J]. 安全与环境工程, 2019, 26(2): 111-116. Qian H, Yang S, Peng QQ, et al. Risk assessment of pressure test system under high voltage based on fuzzy analytic hierarchy process[J]. Saf Environ Eng, 2019, 26(2): 111-116. DOI:10.13578/j.cnki.issn.1671-1556.2019.02.016 |
| [4] |
段秉乾, 司春林. 基于模糊层次分析法的产品创新风险评估模型[J]. 同济大学学报: 自然科学版, 2008, 36(7): 1002-1005. Duan BK, Si CL. Comprehensive risk assessment model of complex product systems innovation based on Fuzzy AHP[J]. J Univ Tongji: Natural Science, 2008, 36(7): 1002-1005. DOI:10.3321/j.issn:0253-374X.2008.07.028 |
| [5] |
Zhang H, Li W, Miao P, et al. Risk grade assessment of sudden water pollution based on analytic hierarchy process and fuzzy comprehensive evaluation[J]. Environ Sci Pollut Res Int, 2020, 27(1): 469-481. DOI:10.1007/s11356-019-06517-9 |
| [6] |
Tripathi AK, Agrawal S, Gupta RD. Comparison of GIS-based AHP and fuzzy AHP methods for hospital site selection: a case study for Prayagraj City, India[J]. GeoJournal, 2021, 1-22. DOI:10.1007/s10708-021-10445-y |
| [7] |
Lin Q, Wang D. Facility layout planning with SHELL and Fuzzy AHP method based on human reliability for operating theatre[J]. J Healthc Eng, 2019, 2019: 8563528. DOI:10.1155/2019/8563528 |
| [8] |
Hancerliogullari G, Hancerliogullari KO, Koksalmis E. The use of multi-criteria decision making models in evaluating anesthesia method options in circumcision surgery[J]. BMC Med Inform Decis Mak, 2017, 17(1): 14. DOI:10.1186/s12911-017-0409-5 |
| [9] |
Samanlioglu F, Kaya BE. Evaluation of the COVID-19 pandemic intervention strategies with hesitant F-AHP[J]. J Healthc Eng, 2020, 2020: 8835258. DOI:10.1155/2020/8835258 |
| [10] |
蔡娟娟, 申俊龙, 黄建元. 基于模糊层次分析法的南京市某医院中药制剂定价方法研究[J]. 医学与社会, 2015(4): 75-78. Cai JJ, Shen JL, Huang JY. Research on the traditional Chinese medicine preparation pricing method in a Nanjing hospital based on Fuzzy AHP method[J]. Med Society, 2015(4): 75-78. DOI:10.13723/j.yxysh.2015.04.024 |
| [11] |
马莹, 褚淑贞. 基于SCOR模型的药品配送风险多级模糊综合评价[J]. 中国药业, 2018, 27(13): 66-69. Ma Y, Chu SZ. Multi-level fuzzy comprehensive evaluation of drug distribution risk based on SCOR model[J]. China Pharm, 2018, 27(13): 66-69. DOI:10.3969/j.issn.1006-4931.2018.13.021 |
| [12] |
殷小娟, 赵煜红, 苏晓燕, 等. 甘肃省定西市法定传染病流行特征及发病趋势[J]. 疾病预防控制通报, 2017, 32(3): 29-32. Yin XJ, Zhao YH, Su XY, et al. Epidemiological characteristics and incidence trend of notifiable infectious diseases in Dingxi city, Gansu province[J]. Bull Dis Control Prev (China), 2017, 32(3): 29-32. DOI:10.13215/j.cnki.jbyfkztb.1610004 |
| [13] |
王哲, 任婧寰, 李树萍, 等. 云南省鲁甸地震灾区重点传染病风险评估[J]. 中国公共卫生管理, 2015, 31(2): 182-184. Wang Z, Ren JH, Li SP, et al. Preliminary assessment on risk of priority communicable disease in earthquake hit area in Ludian, Yunnan province[J]. Chin J PMH, 2015, 31(2): 182-184. DOI:10.19568/j.cnki.23-1318.2015.02.021 |
| [14] |
邓雪凌. 非齐次Hawkes模型在传染病实时预测中的应用[J]. 调研世界, 2021(2): 9-18. Deng XL. Non-homogeneous Hawkes model and its application in projections of outbreak size of epidemics[J]. World Surv Res, 2021(2): 9-18. DOI:10.13778/j.cnki.11-3705/c.2021.02.002 |
| [15] |
Li X, Liu T, Lin L, et al. Application of the analytic hierarchy approach to the risk assessment of Zika virus disease transmission in Guangdong province, China[J]. BMC Infect Dis, 2017, 17(1): 65. DOI:10.1186/s12879-016-2170-2 |
| [16] |
Tu C, Fang Y, Huang Z, et al. Application of the analytic hierarchy process to a risk assessment of emerging infectious diseases in Shaoxing City in Southern China[J]. Jpn J Infect Dis, 2014, 67(6): 417-422. DOI:10.7883/yoken.67.417 |
| [17] |
蓝泳铄, 宋世斌. 高致病性禽流感发生风险评估模型的建立[J]. 中山大学学报: 医学科学版, 2008, 29(5): 615-619. Lan YS, Song SB. Establishment of a risk assessment model for analysis of spread of highly pathogenic avian influenza[J]. J Sun Yat-Sen Univ: Med Sci, 2008, 29(5): 615-619. DOI:10.3321/j.issn:1672-3554.2008.05.025 |
| [18] |
Sabahi F. Bimodal Fuzzy Analytic Hierarchy Process (BFAHP) for coronary heart disease risk assessment[J]. J Biomed Inform, 2018, 83: 204-216. DOI:10.1016/j.jbi.2018.03.016 |
| [19] |
李霞, 白净, 杨德超, 等. 心血管健康状况的模糊评估方法[J]. 北京生物医学工程, 2006, 25(5): 478-481. Li X, Bai J, Yang DC, et al. Fuzzy method for assessing the health status of cardiovascular system[J]. Beijing Biomed Med Eng, 2006, 25(5): 478-481. DOI:10.3969/j.issn.1002-3208.2006.05.008 |
| [20] |
Rajabi F, Jahangiri M, Molaeifar H, et al. Occupational stress among nurses and pre-hospital emergency staff: application of fuzzy analytic hierarchy process (FAHP) method[J]. EXCLI J, 2018, 17: 808-824. DOI:10.17179/excli2018-1505 |
| [21] |
熊彦红, 向芳, 夏尚, 等. 隐孢子虫实验室安全风险评估模型的建立[J]. 中国血吸虫病防治杂志, 2016, 28(6): 678-682. Xiong YH, Xiang F, Xia S, et al. Establishment of a risk assessment model for laboratory biosafety of cryptosporidium[J]. Chin J Schisto Control, 2016, 28(6): 678-682. DOI:10.16250/j.32.1374.2015219 |
| [22] |
Honarbakhsh M, Jahangiri M, Farhadi P. Effective factors on not using the N95 respirators among health care workers: application of Fuzzy Delphi and Fuzzy Analytic Hierarchy Process (FAHP)[J]. J Healthc Risk Manag, 2017, 37(2): 36-46. DOI:10.1002/jhrm.21286 |
| [23] |
陈潇潇, 李玲玲, 汪剡灵, 等. 男男性行为者个体HIV感染风险评估工具预测能力分析[J]. 中华流行病学杂志, 2020, 41(8): 1324-1327. Chen XX, Li LL, Wang YL, et al. Predictive ability of risk assessment tool regarding HIV infection for men who have sex with men[J]. Chin J Epidemiol, 2020, 41(8): 1324-1327. DOI:10.3760/cma.j.cn112338-20191011-00728 |
| [24] |
汤后林, 毛宇嵘, 吴尊友. 应用贝努利过程模型拟合艾滋病病毒感染单阳家庭配偶间性传播及干预措施效果分析[J]. 中华流行病学杂志, 2018, 39(6): 755-759. Tang HL, Mao YR, Wu ZY. Application of Bernoulli process model fitting the effect of intervention measures on sexual transmission among HIV sero-discordant couples[J]. Chin J Epidemiol, 2018, 39(6): 755-759. DOI:10.3760/cma.j.issn.0254-6450.2018.06.012 |
| [25] |
汤后林, 刘玉芬. 夫妇单方艾滋病病毒感染家庭生育问题研究[J]. 中国计划生育学杂志, 2019, 27(4): 535-538, 543. Tang HL, Liu YF. Research of fertility of couples with HIV infection sero-discordant[J]. Chin J Fam Plann, 2019, 27(4): 535-538, 543. DOI:10.3969/j.issn.1004-8189.2019.04.034 |
 2022, Vol. 43
2022, Vol. 43


