文章信息
- 郑棒, 刘琪, 吕筠, 余灿清.
- Zheng Bang, Liu Qi, Lyu Jun, Yu Canqing
- 降秩回归方法简介及其Stata程序开发
- Introduction of reduced rank regression and development of a user-written Stata package
- 中华流行病学杂志, 2022, 43(3): 403-408
- Chinese Journal of Epidemiology, 2022, 43(3): 403-408
- http://dx.doi.org/10.3760/cma.j.cn112338-20210222-00136
-
文章历史
收稿日期: 2021-02-22
2. 北京大学公众健康与重大疫情防控战略研究中心, 北京 100191;
3. 帝国理工学院公共卫生学院, 英国伦敦 W6 8RP
2. Peking University Center for Public Health and Epidemic Preparedness & Response, Beijing 100191, China;
3. School of Public Health, Imperial College London, London W6 8RP, UK
降秩回归(reduced rank regression,RRR)是一种多变量统计方法,在使用多个自变量预测或解释多个因变量的同时达到降维的目的[1-2]。降秩回归在国内外文献中大多特指降秩线性回归,即在传统多变量线性回归的基础上进行的拓展。传统多变量线性回归通过估计自变量的线性组合拟合多个因变量,其线性组合的个数与因变量的个数相等。而降秩回归通过估计少于因变量个数的相互独立的自变量线性组合(降秩回归因子),最大程度解释因变量组的变异。
降秩回归近年来被广泛应用到了医学领域,尤其是营养流行病学中基于特定的因素提取膳食模式(即各类食物摄入量的线性组合)[3-5]。Hoffmann等[3]在欧洲肿瘤与营养前瞻性队列(European Prospective Investigation into Cancer and Nutrition)的Potsdam子队列中应用了该方法。他们使用49个食物组的摄入量数据预测4个糖尿病相关的营养素摄入指标(多不饱和脂肪酸与饱和脂肪酸摄入量比值、纤维素摄入量、镁摄入量、酒精摄入量),从而得到了一个与糖尿病患病风险有关联的膳食模式。目前国内使用降秩回归进行流行病学分析的研究较少。殷召雪等[6]和程茅伟等[7]分别用降秩回归得到了血压值(SBP和DBP)和代谢综合征生物标记物(腰围、SBP、DBP、TG、HDL-C、FPG)相关的膳食模式,并利用这些膳食模式研究食物摄入与疾病风险的关联。值得注意的是,本文所提及的膳食模式是指为了预测一组因变量(如生物学指标)而对一组膳食摄入自变量的综合(即线性组合),而不是通过对膳食摄入变量做因子分析而得到的隐变量。
一、降秩回归方法介绍降秩回归是一种用于降维的多变量线性回归,适用于存在多个相关性较强的连续型因变量的情况。其在传统多变量线性回归的假设基础上,对回归系数矩阵或预测值矩阵的秩加以限制。假设自变量个数为p(即自变量组:X1,…,Xp),因变量个数为q(即因变量组:Y1,…,Yq),样本量为n,自变量矩阵X(n×p)与因变量矩阵Y(n×q)均满秩,且n > p≥q。传统的普通最小二乘估计(ordinary least squares,OLS)的目标是使残差平方和最小,即求解回归系数矩阵B(p×q),使得L=∥Y-XB∥2最小。其中预测值矩阵用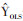
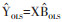
降秩回归方法对回归系数矩阵B(p×q)的秩进行限制,要求在B的秩m≤q的前提下,使残差平方和最小。这等同于求解m个不存在共线性的自变量线性组合(即m个降秩回归因子),来解释因变量组的变异。该求解过程[1-2, 8-9]可以通过对普通最小二乘法得到的预测值矩阵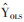
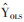
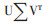
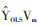
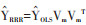
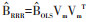
特别的,在规定m=q的情况下,降秩回归能提取出q个自变量线性组合但不能起到降维的作用,此时其优点是这q个变量相互线性独立。而在规定m < q的情况下,对秩次的这一限制则能体现降秩回归的降维作用。在现实情况下,使因变量组的预测残差平方和最小的秩次数为q,因为每减少一个秩次,预测变量的数量(即可以使用的预测信息)就会减少,对因变量组的拟合效果就会变差。因此降秩回归中对秩次m的选择是在降维和拟合度之间的取舍与平衡。此外,降秩回归是多变量统计方法,如果只有一个因变量(q=1),降秩回归的结果就等同于一般线性回归的结果。
二、降秩回归的软件实现与Stata程序开发1. 降秩回归的软件实现:目前,主流的统计分析软件开发了降秩回归的程序或者宏。SAS软件的偏最小二乘(PLS)过程或高性能偏最小二乘(HPPLS)过程可以实现降秩回归(proc pls data=data method=RRR或proc hppls data=data method=RRR)[10]。R语言的rrr包[11]和rrpack包[12]也可以实现降秩回归。然而,Stata软件目前尚无进行降秩回归的独立程序或命令,仅有的Stata程序(PLSSAS)是通过调用SAS软件实现的[13]。
基于以上情况,笔者开发了用于实现降秩回归的Stata程序(rrr),并提交到了波士顿大学“统计软件组件存档”[Statistical Software Components(SSC)archive][14]。读者可以通过在Stata软件里直接输入“ssc install rrr”语句安装,该程序包含程序代码(rrr.ado)和帮助文件(rrr.sthlp)[14]。
2. Stata程序开发原理:Stata程序rrr是按照降秩回归方法的基本思想进行原生开发,即对OLS预测值矩阵
其原理和步骤:①利用Stata软件的regress命令,分别用自变量组对每个因变量进行一般线性回归,进而用predict语句得到线性预测值
此外,分析中还可以使用regress命令,以提取的降秩回归因子对自变量组做线性回归,从而根据该模型的回归系数(即因子载荷)得到降秩回归因子的计算公式。
3. Stata程序功能介绍:rrr程序的主体语句形式是:rrr depvars [if] [in],x(indepvars)[rank()nostd savevar loadings]。其中因变量名列表和自变量名列表是必要语句,还可以选择是否需要筛选纳入样本、设定秩次、进行变量标准化、保存中间变量以及因子载荷输出(语句中的[]内的部分),详细说明见表 1。
程序运行后,Stata软件在界面依次输出分析结果,包括OLS回归的参数估计结果、因变量OLS预测值的描述性统计、主成分分析结果、降秩回归因子对原始变量的方差解释百分比以及因子载荷等信息。
与此同时,程序将分析过程中新生成的变量保存在原始数据集中,包括提取的降秩回归因子、标准化后的自变量和因变量、因变量的OLS预测值等变量,具体变量解释见表 2。
本文利用中国慢性病前瞻性研究(China Kadoorie Biobank)[16]第二次重复调查的膳食数据作为实例,介绍降秩回归和rrr程序的应用。此研究纳入25 041名调查对象(平均年龄为59.5岁,女性占61.8%),通过对血压值和膳食摄入量做降秩回归来得到血压相关的膳食模式。因变量为SBP[变量名sbp,平均值为136.6 mmHg(1 mmHg=0.133 kPa)]和DBP(变量名dbp,平均值为78.3 mmHg),自变量为10个食物组的摄入量(大米、面食、杂粮、肉类及制品、家禽及制品、鱼类/海产品、蛋类及制品、新鲜蔬菜、豆制品、新鲜水果)。Stata语句如下:
rrr sbp dbp,x(rice wheat other_staple meat poultry fish eggs fresh_veg soya fresh_fruit)loadings
Stata输出结果主要分为三部分:①变量数汇总和一般线性回归结果;②主成分分析结果;③提取的降秩回归因子分别对因变量和自变量的方差解释百分比(图 1)。从结果可得,提取的两个降秩回归因子(膳食模式)共解释因变量(SBP和DBP)0.9%的变异,第一个因子和第二个因子分别解释因变量0.5%和0.4%的变异。第一个因子解释自变量组10.3%的变异,其中与肉类及制品和新鲜水果等食物组相关性相对较强;第二个因子解释自变量组10.1%的变异,其中与面食和豆制品等食物组相关性相对较强。此分析所得的两个降秩回归因子对因变量的方差解释百分比偏低,可能与纳入的食物组较少有关(作为示例分析仅考虑了主要食物组的摄入量)。
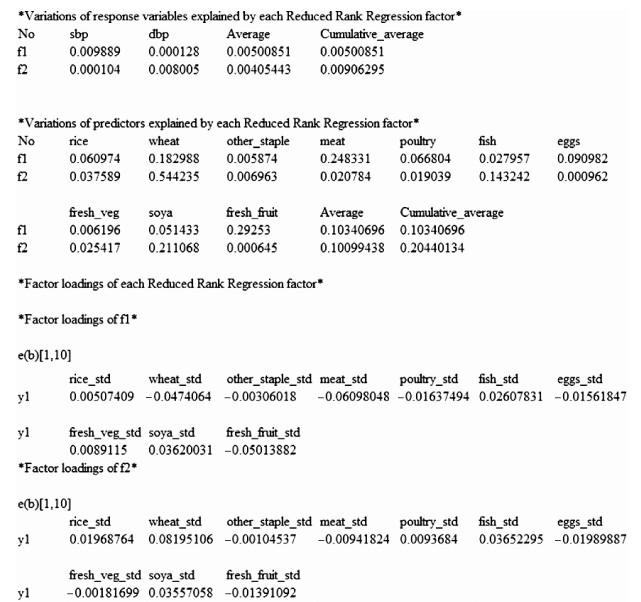
|
| 图 1 rrr程序输出结果:方差解释百分比和因子载荷 |
此外,示范语句中加入了loadings语句以获得每个食物组的因子载荷(图 1)。程序在原数据集里添加的两个降秩回归因子(膳食模式)得分变量f1和f2(表 3),就是通过各食物组的标准化后摄入量与其因子载荷乘积之和计算所得。rrr程序提取的膳食模式因子载荷可被用于计算其他相似的膳食数据中相应的膳食模式得分,例如:
膳食模式1的计算公式:f1=rice_std×(0.005 07)+wheat_std×(-0.047 41)+other_staple_std×(-0.003 06)+meat_std×(-0.060 98)+poultry_std×(-0.016 37)+fish_std×(0.026 08)+eggs_std×(-0.015 62)+fresh_veg_std×(0.008 91)+soya_std×(0.036 20)+fresh_fruit_std×(-0.050 14)。
四、讨论本文介绍了降秩回归方法的基本原理,开发了基于Stata的rrr程序包,并通过中国慢性病前瞻性研究数据进行了膳食模式的示例分析。降秩回归目前主要应用于营养流行病学[17],来研究从食物摄入量到营养素摄入量再到疾病结局的关联通路,或者建立食物摄入量-生物标记物-疾病的关联通路。但是此方法同样适用于其他多变量关联通路的研究方向。
除降秩回归外,还有其他两种常用的多变量降维回归方法:主成分回归和偏最小二乘回归。主成分回归注重于对自变量组变异的解释,用自变量组的主成分得分和因变量组做回归;而偏最小二乘回归则兼顾两者的方差解释,用自变量组的主成分和因变量组的主成分做回归[18]。相较而言,降秩回归更注重于对因变量组变异的解释,其因子得分对因变量的方差解释百分比往往优于另两种方法[3]。值得注意的是,在实际应用中降秩回归秩次数的选择存在一定的主观性。保留的降秩回归因子越多(例如m=q),其对因变量组变异的解释越好(即拟合度越高);保留的降秩回归因子越少,则降维的作用越明显,例如用一个降秩回归因子f1去代表两个因变量(SBP和DBP)的信息。在实际操作中,使用者可以先采用程序默认的满秩设置(秩次等于因变量个数),根据主成分分析的结果并结合实际研究需要来选择想要保留的降秩回归因子的个数。例如考虑保留特征值> 1的因子,或者当从第i个因子开始特征值大幅下降(即第i+1个因子的特征值明显低于第i个因子),则考虑保留前i个因子。
本研究开发了首个采用降秩回归方法分析的Stata程序包,并提交到了Stata程序发布平台SSC,供全球用户使用。本程序准确的实现了SAS软件的降秩回归分析功能。在本文的示例分析中,通过将Stata软件输出结果与SAS软件的PLS(RRR)过程输出结果做横向对比,发现两个软件提取的降秩回归因子对自变量和因变量的方差解释百分比及因子载荷(SAS软件中称为Model Effect Weights)完全一致,而因子得分相差常数倍(f1和f2分别相差0.105倍和0.102倍)。由于降秩回归因子得分没有量纲且其绝对数值没有实际意义,因此是完全等价的结果。
本程序开发的意义首先在于实现了Stata软件用户直接使用该软件做降秩回归的需求。目前Stata是国内外较为常用的统计软件之一,用户群体庞大,并且Stata软件编程语言与SAS、R软件等存在较大差异。在本程序开发前,大多数Stata软件用户只能通过其他软件进行降秩回归分析,因此本程序的开发打破了这一分析工具上的限制。其次,相较于已有的SAS程序和R程序,本程序提供了更为简便、灵活的语句设置。rrr程序只有两个必要输入语句:自变量组和因变量组,因此主体语句结构简洁易懂。此程序不仅遵循Stata官方程序格式,例如可以与if、in等语句兼容,还根据常见分析流程开发扩展选项,例如变量标准化功能。rrr程序默认对变量进行标准化。如果数据已经经过标准化,或各变量的量纲一致,则可在命令中加nostd语句跳过该过程。第三,此程序的输出结果相比于其他已有程序更具系统性和结构性,有助于使用者更好地理解降秩回归的原理及分析步骤(即OLS估计、主成分分析和方差解释百分比计算)。此程序的loadings语句可以指定在运行完rrr程序后输出各个降秩回归因子的因子载荷,构建降秩回归因子的计算公式。该公式可直接应用到其他有相同自变量的数据库来生成降秩回归因子,从而增加研究间的可比性。
综上所述,降秩回归在公共卫生领域有着广泛的应用前景,而Stata程序的开发弥补了该软件用户无法直接使用该统计方法进行数据分析的不足,有助于其进一步推广使用。
利益冲突 所有作者声明无利益冲突
作者贡献声明 郑棒:软件开发、分析解释数据、起草文章、统计分析;刘琪:统计分析、对文章的知识性内容作批评性审阅;吕筠:对文章的知识性内容作批评性审阅、经费支持;余灿清:研究制订、软件开发、分析解释数据、起草文章、经费支持
| [1] |
Izenman AJ. Reduced-rank regression for the multivariate linear model[J]. J Multivar Anal, 1975, 5(2): 248-264. DOI:10.1016/0047-259X(75)90042-1 |
| [2] |
van der Merwe A, Zidek JV. Multivariate regression analysis and canonical variates[J]. Can J Stat, 1980, 8(1): 27-39. DOI:10.2307/3314667 |
| [3] |
Hoffmann K, Schulze MB, Schienkiewitz A, et al. Application of a new statistical method to derive dietary patterns in nutritional epidemiology[J]. Am J Epidemiol, 2004, 159(10): 935-944. DOI:10.1093/aje/kwh134 |
| [4] |
Shakya PR, Melaku YA, Page A, et al. Association between dietary patterns and adult depression symptoms based on principal component analysis, reduced-rank regression and partial least-squares[J]. Clin Nutr, 2020, 39(9): 2811-2823. DOI:10.1016/j.clnu.2019.12.011 |
| [5] |
Frank LK, Jannasch F, Kröger J, et al. A dietary pattern derived by reduced rank regression is associated with type 2 diabetes in an urban Ghanaian population[J]. Nutrients, 2015, 7(7): 5497-5514. DOI:10.3390/nu7075233 |
| [6] |
殷召雪, 任泽萍, 徐小刚, 等. 基于降秩回归的血压相关膳食模式与老年人认知受损的关系[J]. 中华流行病学杂志, 2018, 39(6): 781-785. Yin ZX, Ren ZP, Xu XG, et al. Association between blood pressure related dietary patterns and identified cognitive performance in the elderly Chinese-a study by reduced rank regression method[J]. Chin J Epidemiol, 2018, 39(6): 781-785. DOI:10.3760/cma.j.issn.0254-6450.2018.06.017 |
| [7] |
程茅伟, 王惠君, 王志宏, 等. 基于降秩回归的膳食模式与代谢综合征相关性研究[J]. 营养学报, 2017, 39(2): 121-126. Cheng MW, Wang HJ, Wang ZH, et al. Study on the correlation between dietary patterns and metabolic syndrome based on reduced rank regression analysis[J]. Acta Nutrimenta Sinica, 2017, 39(2): 121-126. DOI:10.3969/j.issn.0512-7955.2017.02.004 |
| [8] |
Anderson TW, Rubin H. Estimation of the parameters of a single equation in a complete system of stochastic equations[J]. Ann Math Stat, 1949, 20(1): 46-63. DOI:10.1214/aoms/1177730090 |
| [9] |
Anderson TW. Estimating linear restrictions on regression coefficients for multivariate normal distributions[J]. Ann Math Stat, 1951, 22(3): 327-351. DOI:10.1214/aoms/1177729580 |
| [10] |
SAS Institute Inc. SAS/STAT® 13.1 User's Guide[EB/OL]. Cary, NC: SAS Institute Inc., 2013. https://support.sas.com/documentation/cdl/en/statug/66859/HTML/default/viewer.htm#titlepage.htm.
|
| [11] |
Addy C. rrr: reduced-rank regression[CP]. (2016)[2021-01-31]. https://CRAN.R-project.org/package=rrr.
|
| [12] |
Chen K, Wang WJ, Yan J. rrpack: reduced-rank regression[EB/OL]. (2019-11-18). https://cran.r-project.org/package=rrpack.
|
| [13] |
Mander A. PLSSAS: Stata module to execute SAS partial least squares procedure (Windows only)[CP/OL]. Statistical Software Components S456810, Boston College Department of Economics, 2007(2012-06-21). https://ideas.repec.org/c/boc/bocode/s456810.html.
|
| [14] |
Zheng B, Yu CQ. RRR: Stata module to perform Reduced rank regression[CP/OL]. Statistical Software Components S458882, Boston College Department of Economics, 2020. https://ideas.repec.org/c/boc/bocode/s458882.html.
|
| [15] |
Kohler U, Luniak M. Data Inspection using Biplots[J]. Stata J, 2005, 5(2): 208-223. DOI:10.1177/1536867X0500500206 |
| [16] |
李立明, 吕筠, 郭彧, 等. 中国慢性病前瞻性研究: 研究方法和调查对象的基线特征[J]. 中华流行病学杂志, 2012, 33(3): 249-255. Li LM, Lv J, Guo Y, et al. The China Kadoorie Biobank: related methodology and baseline characteristics of the participants[J]. Chin J Epidemiol, 2012, 33(3): 249-255. DOI:10.3760/cma.j.issn.0254-6450.2012.03.001 |
| [17] |
程茅伟, 张兵. 应用降秩回归评估膳食模式与代谢紊乱性疾病相关性的研究进展[J]. 营养学报, 2020, 42(1): 83-91. Cheng MW, Zhang B. Application of reduced rank regression in evaluating the association between dietary patterns and metabolic diseases[J]. Acta Nutrim Sin, 2020, 42(1): 83-91. DOI:10.3969/j.issn.0512-7955.2020.01.017 |
| [18] |
罗晓, 陈耀, 孙优贤. 基于统计回归的质量推断方法[J]. 信息与控制, 2001, 30(5): 422-426. Luo X, Chen Y, Sun YX. Statistical-regression-based quality inference methods[J]. Inform Control, 2001, 30(5): 422-426. DOI:10.3969/j.issn.1002-0411.2001.05.008 |
 2022, Vol. 43
2022, Vol. 43





