文章信息
- 高瑞, 于石成, 王琦琦, 周晓华, 刘楠堃, 谭枫.
- Gao Rui, Yu Shicheng, Wang Qiqi, Zhou Xiaohua, Liu Nankun, Tan Feng
- 我国新型冠状病毒肺炎早期时空演变规律分析
- Spatiotemporal evolution of COVID-19 epidemic in the early phase in China
- 中华流行病学杂志, 2022, 43(3): 297-304
- Chinese Journal of Epidemiology, 2022, 43(3): 297-304
- http://dx.doi.org/10.3760/cma.j.cn112338-20211217-00996
-
文章历史
收稿日期: 2021-12-17
2. 北京大学医学部,北京 100191
2. Peking University Health Science Center, Beijing 100191, China
新型冠状病毒肺炎(COVID-19)是由新型冠状病毒引起的一种高传染性的呼吸道疾病。COVID-19已被纳入我国法定乙类传染病,同时采取甲类传染病的防控措施。2019年12月,湖北省武汉市出现COVID-19病例[1]。COVID-19疫情作为重大突发公共卫生事件,严重影响了人民的生命财产和国民经济发展,引起了世界各国的高度重视[2-3]。疫情空间特征的描述和动态传播规律分析是传染病防控研究中的重要技术手段,有助于全面认识疫情的空间传播演化过程,对防控决策的实施提供参考。空间统计学方法可直观、准确地呈现传染病疫情现状和空间分布特征,因此从空间统计视角,挖掘全国COVID-19的空间分布和聚集规律,对有效防控COVID-19疫情具有重要意义。已有研究采用Moran's I和Geary C系数等描述传染病的空间聚集性,可反映疫情空间分布的聚集特征与聚集水平以及发病数与相邻空间上发病数之间的关系。该类方法可有效判断空间区域内是否存在聚集性,但不能精确反映聚集的具体分布和随时间的动态变化规律。而时空扫描分析方法,结合地理信息系统,通过及时统计每一病例的发病时间和地点以及其他重要信息,动态更新疫情分布局势,以及分析疫情发展传播的空间趋势,进而可对疫情的暴发情况进行实时监测和预警。此外,结合每一时期疫情的发展变化趋势,可为疫情防控政策的制定提供参考。目前,已有较多学者对COVID-19的流行病学特征及流行趋势预测模型、病原学和免疫学等方面进行研究,也有一些学者对COVID-19的时空分布规律进行了研究,如阎思宇等[4]通过对COVID-19境外输入确诊病例进行空间自相关分析探讨其空间集聚特征。曹培明等[5]利用地理信息系统(geographic information systems,GIS)制图和一般统计方法,描述性分析了COVID-19在省、市内部的时空特征及其变化趋势。石莹等[6]对中国各省COVID-19累计确诊人数和新增确诊人数进行了全局和局部空间自相关分析,从省级行政区层面探讨了其空间集聚特征。李清清等[7]对广东省各区/县的COVID-19时空扩散特征进行了分析。为了详细了解COVID-19在我国的流行传播规律和空间分布聚集特征,本研究运用GIS技术回顾性分析我国COVID-19地级行政区水平的时空演化规律,通过对我国疫情始发阶段各区域研究单元的COVID-19疫情数据进行空间自相关分析和时空扫描分析,总结疫情的聚集性和发展传播规律,此外,结合不同时期各省份的应急响应等级,揭示各个时期防控干预下疫情发展的空间特征。
资料与方法1. 资料来源:以全国333个地级行政区加上北京、上海、天津、重庆4个直辖市所辖区和30个省直辖县共367个区域研究单元的COVID-19疫情发病资料进行研究(各区域研究单元疫情数据以病例的发病日期进行统计记录),数据来源于中国疾病预防控制信息系统。全国2021版地理信息数据来源于中国国家基础地理信息中心,所需人口数据来源于中华人民共和国第六次人口普查数据。
2. 研究方法:
(1)探索性统计分析:为了方便表达各时段的疫情空间聚集演化和时空聚集特征的变化,从2019年12月8日至12月31日为第一个时段,从2020年1月1日至4月8日以7 d为时间间隔选取时间段,共得到15个时段。利用MATLAB软件绘制新增确诊病例和累计确诊病例的时序图并对其进行分析。
(2)空间自相关分析:利用GeoDa软件,对上述15个时段内各区域研究单元的疫情数据进行空间自相关分析,并绘制可视化疫情图,考察疫情的空间分布和随时段的变化情况。
全局空间自相关用于分析整个研究区域各研究要素的相关程度,用全局Moran's I值来表示,其取值范围为[-1, 1],在P < 0.05即具有统计学意义的前提下,Moran's I > 0为正相关,越接近于1,相关性越强,表示邻接空间单元之间具有明显的相似性或呈聚集性分布;< 0为负相关,越接近于-1,相关性越强,表示邻接空间单元之间差异越大或分布越不集中,接近0则表示邻接空间单元不相关,研究对象在空间上呈随机分布[8-10]。全局统计量的计算公式:
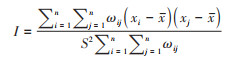 (1)
(1)
 (2)
(2)
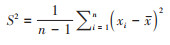 (3)
(3)
式中:I为Moran's I值;xi与xj为区域研究单元i、j的累计确诊人数观测值;x为累计确诊人数观测值的平均值;S2为累计确诊人数观测值的方差;n为区域研究单元个数;ωij为空间权重矩阵,用来度量空间单元之间的邻近关系,相邻时为1,否则为0,其主对角线元素全为0,使用时需对空间权重矩阵进行标准化。分子是对两两区域的“空间权重矩阵×离均差乘积”的值求和,反映了研究区域与相邻区域平均值的共变程度,可看作是考虑了空间位置的协方差。分母表示空间权重矩阵与总体方差的乘积,反映了各区域与研究区域平均值的总变异程度,可看作是考虑了空间位置关系的方差。全局Moran's I值的计算公式考虑了空间位置关系的协方差与方差之比,反映了相邻元素间共变与变异的关系。
全局空间自相关分析的是整个研究区域内COVID-19发病率的相似程度,用来确定全局层面上是否存在聚集区,但不能准确地确定哪些地区存在空间聚集性,以及聚集区和邻接区域之间的关联性。局部空间自相关可展现具体地区的空间分布聚集模式,局部Moran's I值用于反映一个区域研究单元与其邻近区域研究单元的相关程度,根据其和0的比较,分为高-高型(即单元属性值高,相邻单元属性值高)、低-低型(即单元属性值低,相邻的单元属性值低)、高-低型(即单元属性值高,相邻的单元属性值低)和低-高型(即单元属性值低,相邻的单元属性值高)。用LISA集聚图可对局部空间自相关区域进行二维可视化展示。局部Moran's I值的计算公式:
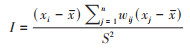 (4)
(4)
式中所有符号的释义同公式(1)。
(3)时空扫描统计:时空扫描统计量方法的基本原理是利用半径随人口数变化的圆柱形窗口在目标区域进行扫描,探测其中可能的发病聚集区域。其中,圆柱形的底对应于地理区域(空间),圆柱形的高对应于时间。在扫描过程中,每个窗口内的期望病例数是根据该窗口内的实际人口数和目标区域的总发病率计算的,再用该窗口的实际发病数和期望发病数计算窗口内的相对危险度(RR)和对数似然比(LLR),LLR最大的为一级聚集区,其余按照LLR值的大小将聚集区分为二、三、四级聚集区等[11]。然后利用马尔可夫链蒙特卡罗(Markov Chain Monte Carlo)方法产生模拟数据集,并得到相应的概率P值,以P < 0.05为差异有统计学意义[12-13]。RR和LLR的计算公式:
 (5)
(5)
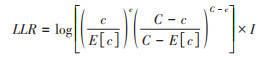 (6)
(6)
式中,c表示窗口内的实际发病例数,C表示目标区域的总发病例数,C-c表示窗口外的实际发病例数,C-E[c]表示窗口外的期望发病例数;E[c]为基于无效假设由协变量校正过的窗口内预期发病数,E[C]为基于无效假设由协变量校正过的预期总发病数;I为扫描值指示值,进行高发病率聚集扫描时,若窗口内实际发病数高于预期发病数,则I=1,反之I=0。
对2019年12月8日至2020年4月8日全国COVID-19资料、全国各省市人口资料以及地理信息资料进行信息提取和处理,使符合SaTScan软件中离散型Poisson分布模型时空扫描方法的资料要求,导入软件中,设置最大扫描半径为总人口的50%,进行时空扫描统计并输出结果。使用MATLAB软件绘制各省份每日确诊病例总数时序图;应用GeoDa软件依据Queen法构建空间权重矩阵,进而计算全局和局部Moran's I值,最后应用SaTScan软件的时空扫描方法探索时空聚集变化趋势及其高发区域和时段。
结果1. 一般情况:对2019年12月8日至2020年4月8日,全国367个区域研究单元累计COVID-19确诊病例62 392例。每日新增确诊病例和累计确诊病例的时间分布曲线见图 1。结果显示,每日新增确诊病例随时间先增长后下降,在2020年1月26日达到峰值,当日新增确诊病例数为3 108例,之后开始下降,至3月7日每日新增确诊病例数降为个位数,之后维持在较低水平,呈平稳、小幅波动状态,下降的过程中,在2月1日突增至3 745例累计确诊病例。
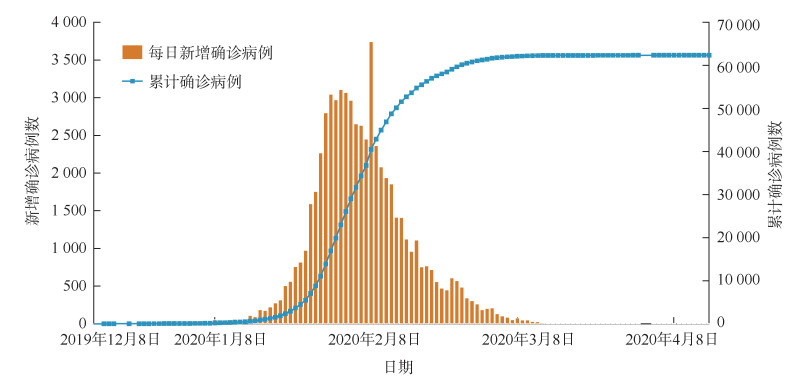
|
| 图 1 中国367个区域研究单元新型冠状病毒肺炎新增和确诊人数变化趋势 |
2. COVID-19空间聚集性分析:
(1)全局空间聚集性:利用式(1)~(3)计算各时段内中国各区域研究单元COVID-19发病率的全局Moran's I值和相关指标,全局Moran's I值在2019年12月8日至2020年1月29日的各时段均为正,且有统计学意义,同时全局Moran's I值随时间的推移逐渐增大,提示该时段各区域研究单元COVID-19发病率总体上具有空间集聚特征,且其聚集程度呈逐渐增强趋势;全局Moran's I值1月30日至2月26日各时段均为正,由0.471减小至0.057,且有统计学意义,提示该时段内COVID-19发病率的总体空间聚集程度减弱;2月27日至3月4日,P=0.021,且Moran's I值趋于0,说明总体空间疫情分布不再具有明显的分布规律,3月5日至4月8日,P > 0.05,全局Moran's I值统计学意义不显著,无法判断疫情空间的分布特征。见表 1。
(2)局部空间聚集性:全局空间自相关研究结果显示,在地级行政区研究层面,全国整体层面上COVID-19发病率的空间聚集性在2019年12月8日至2020年3月4日的10个时间段较为显著,故进一步对该10个时间段的局部聚集特征进行分析,利用公式(4)计算各区域研究单元COVID-19发病率的局部Moran's I值,并通过ArcGIS软件得到局部空间聚集演变图。见图 2。
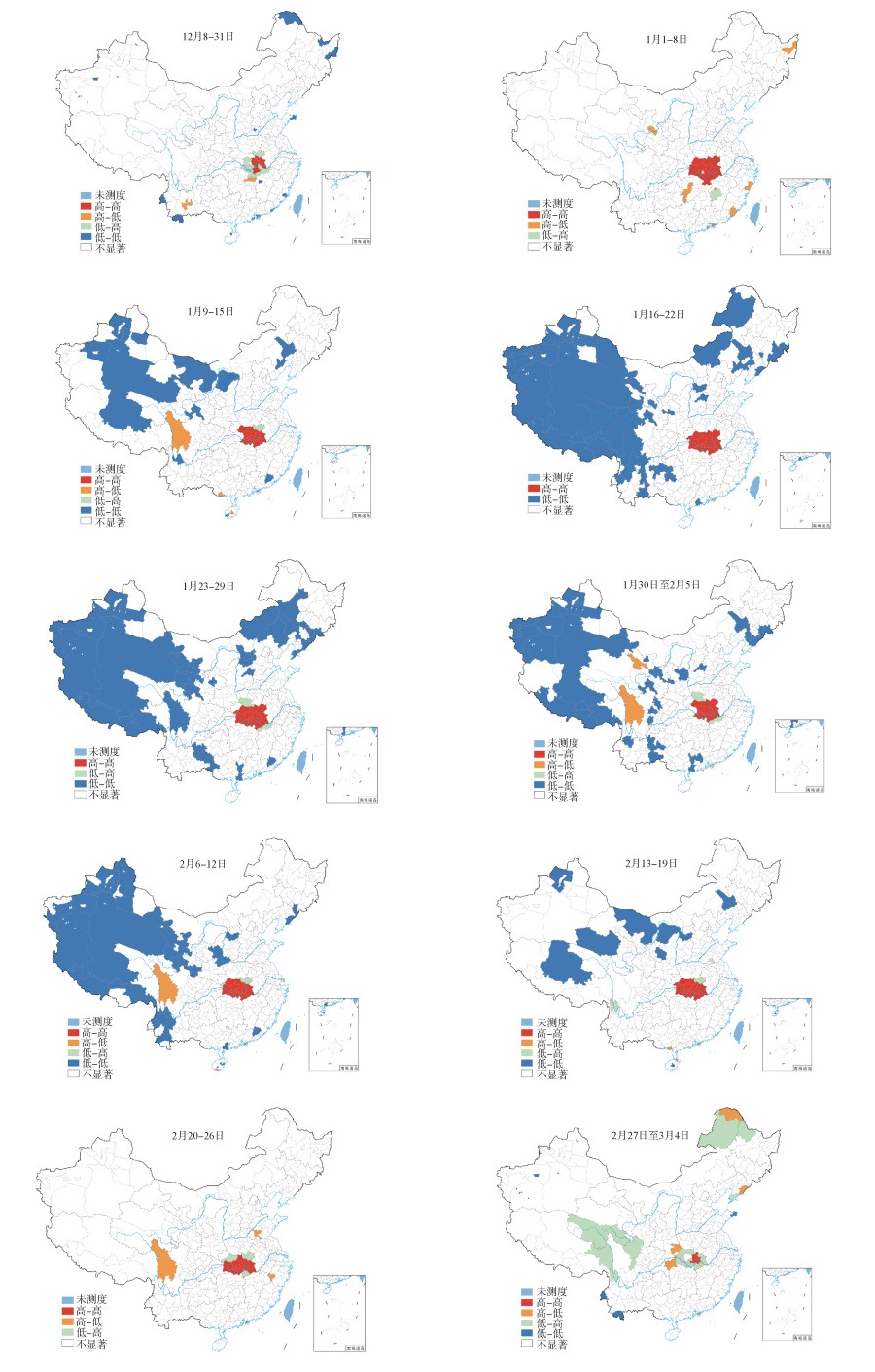
|
| 注:审图号:GS(2022)1351号 图 2 2019年12月8日至2020年3月4日中国新型冠状病毒肺炎局部空间聚集情况 |
高-高聚集区表示该地区与其相邻地区的COVID-19发病率都很高。从局部空间聚集时空分布看,高-高聚集区集中分布在武汉市及其周围区域研究单元,高-高聚集区于2019年12月8日至2020年3月4日均有分布,1月16-29日时段达到最大,共覆盖16个区域研究单元。主要分布在湖北、河南和湖南省,其中湖南省仅在1月1-8日出现,湖北省一直处于此聚集区内。
低-低聚集区说明该地区与其邻近地区的COVID-19发病率都很低。该聚集区在2020年1月23-29日时段达到最大,1月1-8日、2月20-26日我国未出现明显的低-低聚集区,在1月9日至2月19日是4类聚集区中占比最多的聚集区。
高-低聚集区说明该地区COVID-19发病率较高,而其邻近地区较低。2020年1月16-29日我国未出现明显的高-低聚集区,其余时段均有分布。1月1-8日时段高-低聚集区分布的地区最多,离散分布在华东、东北、华中和西北地区的个别区域研究单元;从1月30日至2月5日时段之后集中在华南、西南、华东和西北地区。
低-高聚集区说明该地区COVID-19发病率较低,而其邻近地区较高。2020年1月16-22日我国未出现明显的低-高聚集区,2019年12月8日至2020年2月26日时段覆盖了华中和华东地区,2月13-19日新增加了西南地区,低-高聚集区在2月27日至3月4日时段达到最大,共覆盖19个区域,分布在西南、华中、华北、东北和西北地区。
3. COVID-19时空聚集性分析:应用SaTScan软件对各区域研究单元每日COVID-19新增病例数进行时空扫描分析,即研究COVID-19疫情在时间与空间上聚集性,探测到具有统计学意义的时空聚集区共152个,LLR最大的时空聚集区为一级时空聚集区(包含10个区域研究单元),其余为二级时空聚集区(包含142个区域研究单元)。见表 2。其中一级聚集区有武汉、黄石、鄂州、孝感、黄冈、咸宁、随州、仙桃、潜江、天门等湖北省内城市,LLR=164 847.20,RR=251.04(P < 0.001),表明该聚集区内发病风险是聚集区外风险的251.04倍。一级聚集区聚集时间为2020年1月13日至2月25日,与每日新增发病数的集中时间一致。二级聚集区聚集时间为2020年1月23日至2月1日,该聚集区主要分布在湖北省外以北和以东的部分地区,LLR=103.21,远小于一级聚集区的LLR值,RR=1.31(P < 0.001),表明该聚集区内发病风险是聚集区外风险的1.31倍。由聚集区的时间节点和跨度可知,疫情由起始(2019年12月8日)到出现聚集(2020年1月13日)存在时间间隔,且二级聚集区起始晚于一级聚集区,结束时间早于一级聚集区,时间跨度包含在一级聚集区时间跨度以内。见图 3。
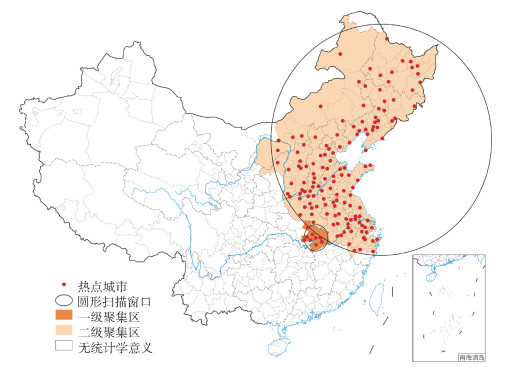
|
| 注:审图号:GS(2022)1351号 图 3 2019年12月8日至2020年4月8日中国新型冠状病毒肺炎时空扫描可视化地图 |
在COVID-19流行早期,人们对此新发传染病缺乏认识,加之病毒传染力强、人员防护意识弱等因素,疫情迅速在武汉市蔓延。1月21日起,全国春运开始,作为国内最早出现疫情聚集情况的武汉市有大量人员流入全国各省市,其中感染者作为其他省市的初始传染源使COVID-19疫情在其他地区也开始传播。1月23日起武汉市关闭离汉通道,成为独立疫情防控地区,聚集情况明显。2020年1月23-25日全国已有30个省级行政区陆续启动突发公共卫生事件一级响应,应对和防控疫情。同时由于各地区初始病例数、地理位置、人口密度、出行频度、气候环境等因素存在差异,以及面对新发疫情的预警程度和防控措施不同,进而导致COVID-19发病数在时间变化和空间分布上存在异质性。本研究应用用空间自相关和时空扫描的方法,探讨全国地级行政区层面上COVID-19疫情的时空分布特征,主要为疫情的时空聚集情况和发展演化规律。
根据每日新增确诊病例和累计确诊病例统计结果可知,发病人数先增加后减少,符合疫情发展防控规律。2月1日突增可能与当时发病诊断标准的更新变化有关。此外也可能由于2月1日前一段时间疫情暴发,暴发地医疗资源有限,出现饱和情况,在2月1日前后进行了病例的集中补充统计。
根据全局空间自相关分析结果,COVID-19发病率的全局Moran's I值呈现先增加后减小的趋势,1月30日前后出现转折,说明空间聚集程度在此之前逐渐增强,随着疫情防控力度的加大,截至1月29日,全国31个省份全部启动突发公共卫生事件一级响应。在1月30日后,各地疫情空间集聚程度逐渐减弱,至3月5日后呈随机分布。全局Moran's I值在2020年1月1日至2月19日时段较大,且有显著统计学意义,提示全国367个区域研究单元COVID-19发病率在总体上具有明显空间聚集性,且为正向空间自相关,即COVID-19发病率较高地区相邻,较低地区相邻。2月20日至3月4日,全局Moran's I值接近于0,说明空间聚集性减弱,空间相关性不再明显,说明全国范围内疫情得到了有效的控制。上述结果与2月21日起,全国陆续下调应急响应等级政策的实施时间相对应。
此外,通过局部空间自相关分析结果可知,高-高聚集区主要分布在湖北、河南和湖南省,这与该区域人口密度高、经济发达、交通便利密不可分,所以很可能是由于人口流动、经济交流、城际交往等原因而导致。随着时间推移,人口流动造成高-高聚集区集中分布于湖北省及周边地区。高-低聚集区大致分布在相对周围人口较为密集的地区,低-低聚集区主要分布在人口密度较低和经济发展水平不高的地区。高-低和低-高聚集的省份总体上增多,这与全局Moran's I值呈现下降的趋势一致。
空间自相关分析具有一定的局限性,其没有考虑时间的因素,只能说明在空间上具有聚集性,而不能判断空间聚集区域随时间变化的趋势。因此引入时空扫描弥补这一不足,时空扫描分析同时考虑了时间和空间两个因素。将每日COVID-19新增病例数进行时空扫描,共得到两类时空聚集区,一级时空聚集区为湖北省内城市,其发病风险是聚集区外风险的251.04倍,聚集时间为2020年1月13日至2月25日,且对应的聚集时间较长,为本次疫情严重区域;二级时空聚集区主要分布在河南省、京津冀等地区,聚集时间为2020年1月23日至2月1日;其余地区没有明显的时空聚集性,即为非聚集区。2月21日起非聚集区所在的各省份陆续下调应急响应等级,截至2月28日,非聚集区应急响应等级基本全部下调为二级及以下。二级聚集区除京津冀外各省份由3月2日起至3月31日应急响应等级全部下调为二级及以下。至4月8日武汉市解封前,全国除京津冀和湖北省外应急响应等级均已降为二级及以下。
全国COVID-19起始阶段早期(2019年12月8日至2020年3月4日)疫情分布具有明显的时空相关性,开始呈现高-高聚集区,主要聚集于湖北省内各区域研究单元,且随着时间推移总体由高-高聚集区变为低-高或高-低聚集区,说明疫情在初始暴发和防控前为自然传播,发病率高,传播区域有限,但在各地政府采取积极防控措施后疫情得到有效控制,病例在地区之间的流动减弱,疫情时空关联性下降。起始阶段后期(2020年3月5日至4月8日)随着病例基数的减少和疫情防控经验的成熟,地区间疫情不再具有明显关联性;通过时空扫描分析结果可知,疫情由始发到暴发存在一定间隔时期,疫情暴发后时空聚集明显,且随人口流动发展传播迅速,二级聚集区开始时间较一级聚集区晚,结束时间较一级聚集区早,主要原因是因为二级聚集区起始病例基本为一级聚集区传入病例,相对基数较小,且一级聚集区启动一级防控措施后,二级聚集区包含省市及时采取一级防控方案,并且疫情暴发前已有一级聚集区的疫情防控经验,且对疫情的传播规律等流行病学特征认识更加全面,进而防控措施更加精准、及时、有效。
与其他相关研究结果相比[14-17],本研究中所用疫情数据为发病日期,而非报告日期,因此能够更真实地描述COVID-19疫情实际的发展传播规律。由于发病日期早于报告日期,与此对应,疫情的暴发日期和转折点均较其他同类研究结果的时间点提前,以此为研究能够更早地了解疫情的发展趋势,及时采取应对措施,缩短疫情的防控周期。此外,本研究将分析结果与实际疫情发展时间节点相对应,结合疫情发展不同时期的应急响应等级的启动和调整时间,可作为防控政策制定的参考依据。
综上所述,本研究利用空间自相关分析发现全国COVID-19发病率具有空间正相关性,存在着明显的聚集区域;通过LISA聚集地图直观展示全国COVID-19发病率的聚集区域,以及不同时段聚集区的变化情况;根据时空扫描分析结果可知不同时期的发病热点区域,结合当时政策措施情况,可验证联防联控机制的有效性,为进一步制定COVID-19及类似呼吸道传染病的有效防控策略,采取相应强度的防控措施提供一定的参考。
利益冲突 所有作者声明无利益冲突
作者贡献声明 高瑞:疫情数据收集、整理、统计分析、绘图、文章撰写;于石成:技术指导、论文修改审核;王琦琦:指导资料分析;周晓华:技术指导;刘楠堃:辅助处理地图相关事宜;谭枫:论文审核、指导
| [1] |
Huang CL, Wang YM, Li XW, et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China[J]. Lancet, 2020, 395(10223): 497-506. DOI:10.1016/S0140-6736(20)30183-5 |
| [2] |
World Health Organization. WHO director-general's opening remarks at the media briefing on COVID-19-11 March 2020[EB/OL]. (2020-03-11)[2021-12-15]. https://www.who.int/director-general/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---11-march-2020.
|
| [3] |
World Health Organization. Situation report-79[EB/OL]. (2020-04-08)[2021-12-15]. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200408-sitrep-79-covid-19.pdf?sfvrsn=4796b143_6.
|
| [4] |
阎思宇, 靳英辉, 王永博, 等. 常态化疫情防控阶段中国内地COVID-19境外输入确诊病例时空分布特征分析[J]. 现代预防医学, 2021, 48(13): 2305-2308. Yan SY, Jin YH, Wang YB, et al. Analysis of spatiotemporal distribution characteristics of COVID-19 imported confirmed cases in mainland China during the stage of normalized epidemic prevention and control[J]. Mod Prev Med, 2021, 48(13): 2305-2308. |
| [5] |
曹培明, 李晓旭, 严晓峰, 等. 重庆市223例新型冠状病毒肺炎病例的回顾性流行病学分析[J]. 西南大学学报: 自然科学版, 2020, 42(3): 10-16. Cao PM, Li XX, Yan XF, et al. Retrospective epidemiological analysis of 223 cases of novel coronavirus pneumonia in Chongqing[J]. J Southwest Univ: Nat Sci Ed, 2020, 42(3): 10-16. DOI:10.13718/j.cnki.xdzk.2020.03.002 |
| [6] |
石莹, 柏如海, 李蕾, 等. 全国新型冠状病毒肺炎空间分布及空间聚集性浅析[J]. 中国循证心血管医学杂志, 2020, 12(2): 148-151, 154. Shi Y, Bai RH, Li L, et al. A brief analysis of the spatial distribution and clustering of COVID-19 in China[J]. Chin J Evid-Bases Cardiovasc Med, 2020, 12(2): 148-151, 154. DOI:10.3969/j.issn.1674-4055.2020.02.05 |
| [7] |
李清清, 高铭, 郑沾福, 等. 广东省COVID-19疫情的空间流行病学分析[J]. 重庆医科大学学报, 2020, 45(7): 904-910. Li QQ, Gao M, Zheng ZF, et al. Spatial epidemiological analysis of coronavirus disease 2019 in Guangdong province[J]. J Chongqing Med Univ, 2020, 45(7): 904-910. DOI:10.13406/j.cnki.cyxb.002586 |
| [8] |
苏理云, 郭雯. 中国各省新型冠状病毒肺炎累计确诊人数的空间聚集及时空格局演变分析[J]. 重庆理工大学学报: 自然科学版, 2020, 34(4): 51-58, 65. Su LY, Guo W. Spatial aggregation and spatial-temporal pattern of provincial cumulative confirmed count of novel coronavirus pneumonia (COVID-19) in China[J]. J Chongqing Inst Technol: Nat Sci Ed, 2020, 34(4): 51-58, 65. DOI:10.3969/j.issn.1674-8425(z).2020.04.007 |
| [9] |
黄翠, 陈晓晖, 谢峰, 等. GIS在传染病防控方面的应用[J]. 公共卫生与预防医学, 2017, 28(1): 77-80. Huang C, Chen XH, Xie F, et al. Application of GIS (geographic information system) in infectious diseases control and prevention[J]. J Public Health Prev Med, 2017, 28(1): 77-80. |
| [10] |
Haining R. Spatial data analysis: theory and practice[M]. Cambridge: Cambridge University Press, 2003: 1077.
|
| [11] |
唐咸艳, 周红霞. 扫描统计及其在流行病学中的应用[J]. 中国卫生统计, 2011, 28(3): 332-337. Tang XY, Zhou HX. Scanning statistics and its application in epidemiology[J]. Chin J Health Stat, 2011, 28(3): 332-337. DOI:10.3969/j.issn.1002-3674.2011.03.042 |
| [12] |
Kulldorff M, Huang L, Pickle L, et al. An elliptic spatial scan statistic[J]. Stat Med, 2006, 25(22): 3929-3943. DOI:10.1002/sim.2490 |
| [13] |
缪羽晨, 刘尧成. 我国华中地区区域经济发展差异比较研究[J]. 经济视角, 2019(6): 67-73. Miao YC, Liu YC. comparative research on economic developmental difference of central China[J]. Econom Vis, 2019(6): 67-73. |
| [14] |
杨瑛莹, 詹思怡, 姜棋竞, 等. 中国258个城市新型冠状病毒肺炎时空分布特征研究[J]. 疾病监测, 2020, 35(11): 977-981. Yang YY, Zhan SY, Jiang QJ, et al. Spatiotemporal characteristics of coronavirus disease 2019 in 258 cities in China[J]. Dis Surveill, 2020, 35(11): 977-981. DOI:10.3784/j.issn.1003-9961.2020.11.005 |
| [15] |
Wu ZY, McGoogan JM. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: summary of a report of 72 314 cases from the Chinese center for disease control and prevention[J]. JAMA, 2020, 323(13): 1239-1242. DOI:10.1001/jama.2020.2648 |
| [16] |
金安楠, 李钢, 王皎贝, 等. 深圳市新型冠状病毒肺炎(COVID-19)疫情时空演化与防控对策[J]. 陕西师范大学学报: 自然科学版, 2020, 48(3): 18-32. Jin AN, Li G, Wang JB, et al. Spatio-temporal evolution and control strategies of COVID-19 epidemic in Shenzhen, China[J]. J Shaanxi Normal Univ: Nat Sci Ed, 2020, 48(3): 18-32. DOI:10.15983/j.cnki.jsnu.2020.03.017 |
| [17] |
崔芳芳, 何贤英, 高景宏, 等. 河南省1 272例新型冠状病毒肺炎流行病学特征[J]. 中华医院感染学杂志, 2020, 30(15): 2247-2251. Cui FF, He XY, Gao JH, et al. Epidemiological characteristics of COVID-19 with 1 272 cases in Henan province[J]. Chin J Nosocomiol, 2020, 30(15): 2247-2251. DOI:10.11816/cn.ni.2020-200694 |
 2022, Vol. 43
2022, Vol. 43