文章信息
- 李亚欣, 牟育彤, 黄卓英, 周晓钰, 郭阳, 孙晓冬, 郑英杰.
- Li Yaxin, Mu Yutong, Huang Zhuoying, Zhou Xiaoyu, Guo Yang, Sun Xiaodong, Zheng Yingjie
- 比例和率:概念内涵及其识别路线
- Proportion and rate: connotation and understanding route
- 中华流行病学杂志, 2022, 43(1): 105-111
- Chinese Journal of Epidemiology, 2022, 43(1): 105-111
- http://dx.doi.org/10.3760/cma.j.cn112338-20210412-00307
-
文章历史
收稿日期: 2021-04-12
2. 上海市疾病预防控制中心,上海 200032;
3. 北京大学深圳医院,深圳 518036
2. Shanghai Municipal Center for Disease Control and Prevention, Shanghai 200032, China;
3. Peking University Shenzhen Hospital, Shenzhen 518036, China
人群流行病学是研究人群中健康相关状态和/或事件的分布及其原因,并提出改变这种分布的策略和措施的科学,除了聚焦于人群的疾病或健康外,与其他群体学科如统计学、人口学、心理学等无异。人群资料有定量和分类之分,其中分类资料的计算建立在以时间为基础的人群事件数、状态数及其来源人群上,由此形成3个基本指标——比、比例和率,而后可演化出不同学科需要的、丰富的分类指标体系。这既是人群研究所期望的,又是当前各类教材编写或具体教学实施所采用的主流路线。
一、比、比例和率的历史与现状比和比例的概念和运算记载于我国古代数学专著《九章算术》,最早可追溯至公元前4世纪的黄金分割理论。广义的“比”是任意两个数值之商,比例和率为其特例。为了与“比例”区分,流行病学将“比”的含义限制于:两个彼此分离的、互不重叠或包容的量之商[1-2],其分子和分母的量纲可相同或不同,如移植器官的供需比、身高与体重之比等。“比”的概念,简单而清晰;然而,对于“比例”和“率”的含义及表述,不同学科之间、不同指标之间不尽相同。
英文名称“proportion”至少有2种中文译名[3-5]:构成比(例)和比例;反之,中文的“构成比”,则出现至少3种英文译名[6-7]:constitution ratio,proportion和proportional ratio。不论是哪个名词,其含义均指的是事物的局部与整体之商或比重[3-4]。从名称的表述上,也有用“率”表述“proportion”的含义,如(时点)患病率,或者累积发病率、罹患率,后者的“率”的含义多数反映事件发生的风险或概率,又常常被认定为是“频率”[6]。名称的混用导致了“以比代率”的问题,究其原因是人们未能辨别状态的存在和事件的发生二者间含义的差别。
此外,“率”又被用于表述变化率(rates of change,R)或速度[1-2, 8-9],以反映两个变量间相互依赖的关系,即一个变量(y)的变化量(Δy)与另一个变量(x)的变化量(Δx)之商,见公式(1)。这个数学定义最早可追踪至1627年提出的“差分(=导数)”概念,至今没有改变[8-10]。
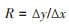 (1)
(1)
“率”的含义在人群研究中的使用,可追溯至1693年英国天文学家埃德蒙·哈雷博士的第一张寿命表[11]或1825年英国保险统计师本杰明·贡培兹提出的“Intensity of Mortality”[12-13]。由于y可以是频数、频率、体重等表示任何含义的量,x可以是时间相关或无关的量,因此率的指标无统一的表达式[13]。在人群事件发生的描述上,虽然威廉·法尔于1838年就以“死亡概率(probability of dying)”和“死亡率(rate of mortality)”明确地区分了风险和率的精确含义[14-15],然而历经多个学者的阐述与澄清[1, 15-17],这两个概念的争议、误解和误用仍在延续[16]。
综上,比例和率的多重而交叉的含义,模糊了其概念的准确性。本文尝试从事件的发生和状态的存在出发,引入一些新的概念,并基于数学上“率”的一般含义,以澄清比例和率的精确内涵,建立其识别路线。
二、两个基本问题——事件的发生和状态的存在事件的发生涉及两个不同状态(如从无病状态向有病状态)的相变过程[18],这个过程通常是瞬间的;然而事件发生后需要一定的时间长度(或时期)才可被我们识别,这意味着事件的计数受到时期的影响,具有时间累积的特征;而物体的某一属性在一定时间内持续,则意味着该物体处于该属性的状态,因此状态本身隐含了时期的概念[19],是历史某一未知时点开始直至现在的结果。只有区分事件的发生过程和事件发生后状态的存在,才能真正理解人群分类资料的基本指标。
例如,统计学在概率的介绍上有两个基本问题:
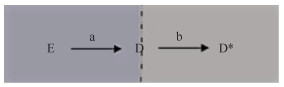
1。彩色球问题:从一袋混有红色、蓝色和绿色球的袋子中随机抽取若干个,红色球出现的概率是多少? 这一问题中,球的色彩(涂色)是历史上已经发生的事件,目前球的颜色性质持续不变。彩色球问题的实质在于了解历史已发生的事件在当前所处的状态特征,仅涉及测量过程(图 1)。
|
| 注:a:事件的发生过程;b:事件的测量过程 图 1 事件的发生和状态的存在及其测量过程 |
2。抛硬币问题:抛硬币若干次,出现正面的概率是多少? 这一问题中,硬币未抛出前,硬币出现正面(或反面)的事件尚未发生;抛硬币过程结束后,目测其是否正面。显然,这个问题涉及了从可能发生(或易感性)且尚未发生到真实发生及发生后的测量,其目的在于了解尚未发生的某一事件在未来发生的可能性,涉及发生和测量两个过程(图 1)。
研究时,若只关注图 1中D→D*的过程,则为对已发生历史事件所处状态的探索,对应于上述的彩色球问题;而若外部力量(E)(如抛起硬币)影响D的发生,并实现后者的测量(D*),则对应于上述的抛硬币问题。
由上可见,从测量起点的角度来看,事件的未来发生或其相变后状态的存在具有时期性,而当前时点(无时间长度)的状态可被视为已发生的历史事件——相变后状态遗留至当前这一刻。以时点测量此刻状态数,即时点状态数(number of states in point time,简写为s0,单位:例)可反映当前时点的情形。若要测量一段时期的所有状态数,即为时期状态累积数(cumulative number of states in period time,简写为s1,单位:例)。
唯有易感者才可相变,即意味着事件的发生[18];唯有对相变前后两个时点不同状态的测量,可获得“事件是否发生”的结果。这提示了在相变前,事件发生数、事件累积数和相变后状态累积数均为零。因此提出了概念“相变后状态累积数的变换量(the change cumulative number of states,简写为Δs/Δt,单位:例/时间)”,其在数量上等价于时期(两个不同时点间)事件发生数或时期状态累积数的变换量。这个概念相当于流行病学等教材中提及的时期事件发生数,如“一定时期内某人群中某病新发病例数”“观察期内某病新发病例数”“潜伏期内易感接触者中发病人数”等。
以上阐述建立了时点状态数、时期状态累积数及其变化量(对应于事件发生数)的概念,时点状态数具有历史累积而遗留的特征;时期状态累积数的变换量具有未来发生并在观察期内累积的特征,时期终点和起点状态累积数之差在数量上相当于时期事件发生数,与通常提及的“观察期新发病例数”类似。当进行时期状态累积数的计数时,如时期患病率,系历史累积遗留至今的时点状态数和未来将要产生的时期事件发生数的综合。由此,人群频率指标的测量统一于“状态”这个概念上。
三、时点状态累积数设有一个封闭人群,包含已发生某事件和在观察期内可能发生某事件的个体。为简化阐述,假设研究的目标是单次事件,并且观察期内无失访、竞争风险等。
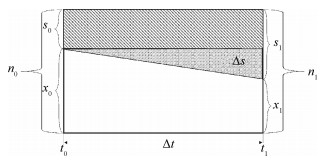
定义以下变量(按照文中出现顺序依次排列),并作简单图示(图 2):ti为第i个观察时点,t0和t1分别为观察起点和终点;Δt为总观察期,如Δt=t1-t0;xi为ti时点的易感个体数;si为ti时点已发生某事件(或处于事件发生的相变后状态)的个体累积数;ni为ti时点观察人群,为易感个体数和个体状态累积数之和,即ni = xi + si;Δni为第i次调查时增加的调查个体数;Δsi为第i次调查时在增加的调查个体数中将出现具有某一状态的个体累积数的变化量;Pi为第i次调查时具有某一状态的个体累积数的变化量,占本次调查所增加的调查个体数的比例;P0为某一时点具有某一状态的个体占全部调查人群的比例;P为时期事件发生比例;P1为时期所有状态累积数占其来源人群的比例。
|
| 图 2 封闭人群在观察期(Δt)内事件发生数和状态累积数 |
在观察期起点(t0)的易感个体x0,经过一个观察期(Δt)后,事件发生(相变后)状态累积数的变换量(Δs),可通过观察期起点(t0时点)状态累积数s0和观察期终点(t1时点)的状态累积数s1进行计算,即:
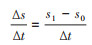 (2)
(2)
此即为通常提及的观察期事件发生数或绝对率(absolute rate),即表示观察期终点和起点状态累积数之差与观察期长度间的关系。例如,每日新型冠状病毒肺炎(新冠)新发病例数300例,是新冠新病例从观察期起点(t0)的0例(s0),经过了一天时间(Δt)的累积后而达到了观察期终点(t1)的300例(s1)。因此,“每日新冠新发病例数”是一天结束时点与这天开始时点的新冠新病例累积数之差与观察期长度的比。
针对观察期起点(t0)的全部个体n0而言,仅有易感个体x0存在事件发生的可能性,产生的事件发生数或相变后状态累积数的变化量(Δs/Δt)。当需要计算观察期(Δt)的所有状态数时,s0可被视为在观察期内保持不变,即:t0时点的状态累积数,在历经一个观察期,其累积数在观察期内不变,在数量上等价于(s0/Δt),从而与Δs/Δt的单位相同而实现可加性。由此可得:
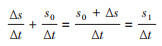 (3)
(3)
此即时期状态累积数或观察期终点状态数,类似于通常提及的“观察期内新旧病例数”,系观察期终点状态累积数与观察期长度之比,或观察期起点状态累积数与观察期间状态累积数变化量之和与观察期长度之比。
由上可见,除时点状态累积数的单位为“例”外,时点状态累积数的变换量和时期状态累积数的单位均为“例/时间”,差别在于:当计算时期状态累积数时,具备观察期(含起点)的状态即可;而计算时期事件发生数时,系两个不同时点状态累积数之差。
四、比例的局部与整体在知晓了时点或时期状态累积数后,通常需要知道其由什么样的人群具有或产生,即明确其来源人群,进而建立“比例”的概念。比例是同一事物局部占整体的比重,有以下3种形式。
1。同一时点的局部与整体:描述某时点的局部与整体之比。由上述可知,进行时点(如t0)观察时,局部(分子,s0)与整体(分母,n0)的同时点性和同单位(均为“例”),故这种比例( 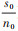
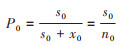 (4)
(4)
需要注意的是,公式4本质上也可被视为“率”的一种特殊形式[13]。如,对患病比例为20%的人群进行调查时,第i次调查时增加100例(Δni)的调查个体,预计将产生20例(Δsi)额外的患者,见公式5,故可将这种比例命名为率型构成比例(rate-type constitutional proportion)。
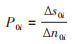 (5)
(5)
从测量的角度来看公式4的计算,可将公式4中s0和n0的测量视为多次公式5所表达过程的实施,即每(第i次)增加人群调查数Δn0i,将新增加Δs0i个具有某一状态的个体(如患病);当测量的整个过程均完成后,ΣΔn0i为已被测量的总体数(n0=ΣΔn0i),ΣΔs0i为已被测量的具有某一状态的个体数之和(s0=ΣΔs0i)。因此,时点构成比例实质上可视为忽略了时间因素影响的多个局部的率型构成比例的综合(图 3),见公式6。
 (6)
(6)
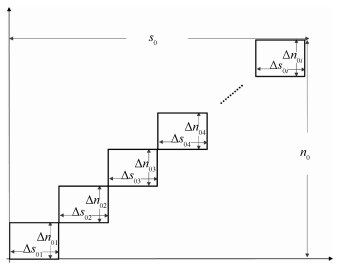
|
| 注:n0代表总体人群;s0代表总体人群中具有某一状态的个体数;Δs0i和Δn0i分别代表第i次增加的人群调查数和具有某一状态的个体数 图 3 时点构成比例与率型构成比例的关系 |
2。时期的局部与时期起点的整体:事件发生的时期性及观察期起点人群的易感性,奠定了指标——时期事件发生比例(incidence proportion,IP)的基础,即:在关闭队列中,观察期起点易感人群(x0),经过一个固定的观察期(Δt)至观察终点,期间状态累积变化量( 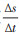
 (7)
(7)
因x0是观察期起点(t0)的易感人群数,为时点概念,其单位为例;故IP是时期概念的分子(Δs/Δt)与时点概念的分母(x0)之商。公式7又可表示为:
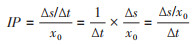 (8)
(8)
由上可见,IP的单位按理应为1/时间。其意义相当于:观察期状态累积变化量(Δs/Δt)占观察期起点易感人群数(x0)之比的时间均值。对上述公式两侧同时乘以Δt而获得:
 (9)
(9)
或
 (10)
(10)
由此可见,IP隐含着将观察期(Δt)视为固定的一个观察期(令Δt=1),故Δt × IP=1×IP = IP,从而将Δt得以从公式中略去;或可以说,Δt发生了移位,即从公式8右侧的分母转移到公式9的左侧,从而出现在IP指标的描述中。因此,IP必须交代观察期(Δt),是固定观察期(Δt=1个单位)的IP。因有意于令Δt=1,故Δt × IP的分子(Δs)包含于分母(x0)之中,取值在[0, 1];当观察时间足够长,IP可达100%。
3。时期的局部与时期的整体:时期状态数是观察期起点状态累积数、观察期终点及起点状态累积数之差的综合(公式3)。假定有一个合适的时期状态数的来源人群(nu),则可将时期状态数占其来源人群的比例命名为时期构成比例(time-period constitutional proportion,P1),见公式11。
与上述IP类似,同样地,其观察期(令Δt=1)将发生移位,并需在指标的描述中提及,见公式12和13。
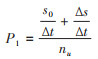 (11)
(11)
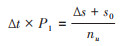 (12)
(12)
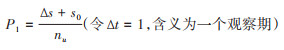 (13)
(13)
那么这个分子的来源人群nu是什么? 对于封闭人群,在观察期起点将人群区分为易感性人群(x0)和历史状态累积数(s0);若整个观察期人群不变,则封闭人群经过一个观察期的状态累积数,其来源人群nu = n0 - s0 + s0 = n0,即nu应为n0,因此,上述公式13可表述为:
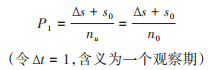 (14)
(14)
由此可见,对于关闭队列而言,当涉及时期的局部与时期的整体之间的关系时,局部的来源人群仍然是观察期起点的人群(含易感人群和已有状态人群),为时点概念;时期患病比例中的分子与分母之间的关系仍是局部与整体间的关系。时期构成比例是时点构成比例和时期发生比例的综合。
五、固定队列(有失访)和动态人群实践中,人群通常存在随时间动态变化的特征,如出现失访、研究终止或易感性缺失等[19],无法确保所有个体均按照一个固定的观察期(Δt)进行观察,个体间观察期的起点和终点可不同,即存在着变化的观察期。
当观察期足够短时,人群中的所有个体应有一个固定的观察期,这为固定队列或动态人群中事件数或状态数的描述奠定基础。因此,固定队列(有失访)或动态人群可被视为:将整个观察期(Δt)细分为i个连续的以Δti为第i个固定观察期的关闭队列,即Δt=ΣΔti。由此,可参照上述情形计算相应的比例指标。实践中,研究感兴趣的通常是整个观察期的频率,以下分别进行阐述。
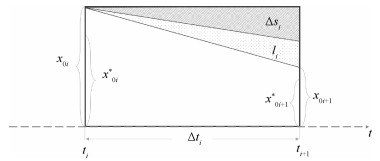
首先定义以下变量,并作简单图示(图 4):Δt为总观察期; Δti为第i个连续的固定观察期,由总观察期Δt细分而成,即Δt = ∑Δti;li为第i个固定观察期内失访个体数;pti为第i个固定观察期内人群观察人时;x0i为第i个固定观察期起点易感个体数;x0i*为第i个固定观察期起点有效易感个体数;Δsi为第i个固定观察期状态累积数变化量。
|
| 图 4 固定队列(有失访)第i个观察期(Δti内事件发生情况 |
1。时期IP:若对第i个观察期的易感人群部分(x0i),在观察期(Δti)内的每一个体进行观察,其中失访者(li)的观察时长常以Δti/2估计,则整个人群经历的观察人时,pti,可表示为:
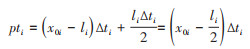 (15)
(15)
由此可将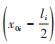

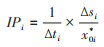 (16)
(16)
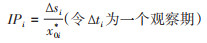 (17)
(17)
公式17构成了Kaplan-Meier或乘积限公式的基础[20]。
2。时期事件发生率(incident rate,IR):由公式16,当我们将∆ti保留于公式中时,x0i*∆ti 是第i个固定观察期事件发生中所贡献人群经历,或人时,以此为分母即可计算时期事件发生率,或可称为相对率(relative rate),即:第i个观察期起点有效易感人群数(x0i*),经过一定的观察期(∆ti)后,该人群事件累积发生数的变化量(∆si)。因此,整个观察期(∆t)内实际事件发生累积数的变化量为∆s = ∑∆si,而观察的总人时为∑xi0*∆ti二者之商(∆t的影响已体现在指标IR的分母——∆ti之中)即:
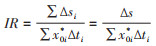 (18)
(18)
这里,x0i*是时点 t0i第i个观察期起点的有效易感人群数(考虑移入移出的影响),单位仍为例;∑x0i* × ∆ti的单位是“例×时间”;因此IR的单位应为“1/时间”。显然,IR只是数学上“率”的一种特殊情形,因“率”指标具有更为灵活地处理人群分类资料的特点,特别适合于多次发生事件,如一年内老年人跌倒的情况,因此其应用领域更为广泛。
3。时期构成比例:以第i个观察期中全人群关闭队列为例,第i个观察期人群的构成比例原则上可仍按照上述“时期的局部与时期的整体”来计算。该指标反映了第i个观察期人群中任一个体具有某一状态的概率,或这概率的时间均值。由于时期构成比例涉及易感者和非易感者可能不同的人群动态变化特征,整个观察期状态比例的计算较为复杂,值得继续进行研究。
至此,我们完成了人群研究的定性资料的指标——比例和率的统一识别路线(图 5):当绝对率结合其来源人群并进行时间分段计算时即转化为IR,当IR的观察期被视为一个单位并移位时即转化为IP,由IP和P0二者综合而成时期构成比例(P1)。

|
| 注:变量的含义见文中;a “比”的概念清晰,不再赘述 图 5 人群频率基本分类及关系 |
本文围绕事件的发生和状态的存在及其测量过程,首先指出了二者的计数有统一的基础——状态;接着提出了“时点状态数和时点状态累积数”的概念,最后发现:率和比例有其固有的结构,二者的概念、联系和区别清晰,容易理解。
人群频率指标的计算,除了状态的时点计数无时间单位(或可将其视为当前时点之前历史累积的遗留)外,涉及时期概念的事件的发生、事件数的变化、状态数及其计数均需要时间,因此人群定性资料的计数具有累积的特征。区分事件(未来)发生的过程和事件发生后状态(历史或相变后)的存在,是理解人群分类资料指标的关键。由此,本文提出了“时点状态数和时点状态累积数”,奠定了频数计数的统一的基础:状态,从而为理解和简化频数指标的计算奠定了坚实的基础。
在本文提出的概念“时点状态累积数的变化量”(单位:例/时间)基础上,从测量的角度揭示了时期事件发生数的计数等价于该时期事件发生后所处于的相变后状态的计数,即时点状态累积数的变化量,这个含义与当前的“(观察期)事件发生数”或“绝对率”是等价的。事件的发生需要一定的观察期(Δt)的特征,形成了发生比例与发生率的联系与区别,即Δt是否被视为一个单位时长的固定期,并移位于指标中观察时长的描述。而时点(或忽视时间的影响)状态的测量,即时点构成比例(亦是率型构成比例)可视为观察人群及其相应状态变化量的累积值间的关系[21],其基础是与时间无关的“率”的含义;在状态为计数基础时,时点构成比例与时期发生比例一起形成了时期构成比例的基础。这种逻辑自然地延伸至动态人群、固定队列和关闭队列中频率指标的估计。由此可见,比例不应具有“率”的含义,“率”也不宜于扮演“比例”的角色,二者适用的统计模型有着本质的差别[22];同时“以比代率”,即“以构成比例替代发生比例”,这个问题也将迎刃而解。
人群疾病频率指标是描述疾病分布、社区诊断、病因推断、干预实施和资源分配的基础,然而其准确性不易保证,这往往因研究设计、经济性等原因而难以获得其必要的计算用元素。因此,对指标的估计是常态,这往往需要满足一定的条件,如人群的稳态性、罕见病假设、随机性失访等;习惯于估计的做法忽视了对指标计算元素的精确理解,或是对指标容易产生误解的原因之一。
人群分类指标的估计上,分子与分母间存在着对应关系尤为重要;然而,要准确界定来源人群(或分母)不太容易[23-26]。基于本文的阐述,容易发现比例和相对率的来源人群均统一于观察期起点人群。因各种原因导致的人群动态变化实质上影响的是其观察期初的有效易感人群数或其相应的人时经历,可通过寿命表等方法进行较为精确的估计[23]。例如,卫生或统计部门计算每年疾病(如肺癌)发病率,对于潜伏期长的癌症而言不太可能在一年内由当年的易感者发生发展而来,这将导致肺癌发病率的计算中存在着“新病例-易感者的对应错位”。实际上,该指标常常使用总人群贡献的观察人时经历的变化量为分母,在稳态人群的条件下以期中人口数或期初和期末人口数均值来估计是合理的(公式18和19)[27]。
 (19)
(19)
综上所述,本文结合人群、时点/时期、状态,基于数学上“率”的一般含义,结合指标计算元素的单位,识别人群计数资料基本指标——比、比例和率的精确内涵,建立统一的、概念明晰、切实可行的指标识别路线,适用于封闭人群、固定队列或动态人群。本文旨在明确指标的含义,无意于改变习惯约定的名称,仅供人群研究工作者参考,如本文提及的“频率”是“率”的概念,但已约定为具有概率(比例)的含义。
利益冲突 所有作者声明无利益冲突
作者贡献声明 李亚欣:研究设计、资料整理、论文撰写;牟育彤、黄卓英、周晓钰:论文修改、技术支持;郭阳、孙晓冬:论文修改;郑英杰:研究设计、论文指导
| [1] |
曾光. 现代流行病学方法与应用[M]. 北京: 北京医科大学、中国协和医科大学联合出版社, 1994. Zeng G. Modern epidemiology methods and applications[M]. Beijing: Beijing Medical University, Chinese Union Medical University Press, 1994. |
| [2] |
王若涛, 罗凤基, 严立. 对疾病分布指标的再认识[J]. 中国卫生统计, 1995, 12(4): 56-57. Wang RT, Luo FJ, Yan L. Rethinking diseases' distribution measuring indexes[J]. Chin J Health Statist, 1995, 12(4): 56-57. |
| [3] |
赵耐青, 陈锋. 卫生统计学[M]. 北京: 高等教育出版社, 2008. Zhao NQ, Chen F. Health statistics[M]. Beijing: Higher Education Press, 2008. |
| [4] |
金丕焕, 陈锋. 医用统计方法[M]. 3版. 上海: 复旦大学出版社, 2009. Jin PH, Chen F. Public health preventive medicine[M]. 3rd ed. Shanghai: Fudan University Press, 2009. |
| [5] |
沈红兵, 齐秀英. 流行病学[M]. 9版. 北京: 人民卫生出版社, 2018. Shen HB, Qi XY. Epidemiology[M]. 9th ed. Beijing: People's Medical Publishing House, 2018. |
| [6] |
钱宇平. 流行病学[M]. 北京: 人民卫生出版社, 1990. Qian YP. Epidemiology[M]. Beijing: People's Medical Publishing House, 1990. |
| [7] |
陆召军, 庄勋. 流行病学[M]. 南京: 东南大学出版社, 2008. Lu ZJ, Zhuang X. Epidemiology[M]. Nanjing: Southeast University Press, 2008. |
| [8] |
同济大学数学系. 高等数学[M]. 7版. 北京: 高等教育出版社, 2014. School of Mathematical Sciences, Tongji University. Advanced mathematics[M]. 7th ed. Beijing: Higher Education Press, 2014. |
| [9] |
孙伟民, 黄大贶. 医用高等数学[M]. 上海: 上海科学技术文献出版社, 1993. Sun WM, Huang DK. Medical advanced mathematics[M]. Shanghai: Shanghai Scientific & Technical Press, 1993. |
| [10] |
Stewart J. Essential calculus[M]. 2nd ed. Belmont: Brooks/Cole, Cengage Learning, 2013.
|
| [11] |
Halley E. An estimate of the degrees of the mortality of mankind, drawn from curious tables of the births and funerals at the city of Breslaw, with an attempt to ascertain the price of annuities upon lives[J]. Philosophical Transactions, 1693, 17: 596-610. DOI:10.1098/rstl.1693.0007 |
| [12] |
Eyler JM. Constructing vital statistics: Thomas Rowe Edmonds and William Farr, 1835-1845[J]. Soz Präventivmed, 2002, 47(1): 6-13. DOI:10.1007/BF01318400 |
| [13] |
Gompertz B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies[J]. Philos Trans Roy Soc London, 1825, 115: 513-583. DOI:10.1098/rstl.1825.0026 |
| [14] |
Vandenbroucke JP. Continuing controversies over "risks and rates"—more than a century after William Farr's "On prognosis"[J]. Soz Präventivmed, 2003, 48(4): 216-218. DOI:10.1007/s00038-003-3073-8 |
| [15] |
Farr W. On prognosis[J]. Br Med lmanack, 1838, 48(4): 199-216. DOI:10.1007/s00038-003-3004-8 |
| [16] |
Elandt-Johnson RC. Definition of rates: some remarks on their use and misuse[J]. Am J Epidemiol, 1975, 102(4): 267-271. DOI:10.1093/oxfordjournals.aje.a112160 |
| [17] |
Vandenbroucke JP. On the rediscovery of a distinction[J]. Am J Epidemiol, 1985, 121(5): 627-628. DOI:10.1093/aje/121.5.627 |
| [18] |
郑英杰, 刘海燕, 于波, 等. 观察与实验: 因果视角[J]. 中华流行病学杂志, 2021, 42(10): 1863-1870. Zheng YJ, Liu HY, Yu B, et al. Observation and experiment: a causal perspective[J]. Chin J Epidemiol, 2021, 42(10): 1863-1870. DOI:10.3760/cma.j.cn112338-20201224-01437 |
| [19] |
Kleinbaum DG, Kupper LL, Morgenstern H. Epidemiologic research: principles and quantitative methods[M]. Belmont, California: Wiley, 1982.
|
| [20] |
Kaplan EL, Meier P. Nonparametric estimation from incomplete observations[J]. J Am Stat Assoc, 1958, 53(282): 457-481. DOI:10.1080/01621459.1958.10501452 |
| [21] |
Miettinen OS. Theoretical epidemiology: principles of occurrence research in medicine[M]. New York: Wiley, 1985.
|
| [22] |
Vose D. Risk analysis: a quantitative guide[M]. 3rd ed. New Jersey: John Wiley & Sons, 2014.
|
| [23] |
Bass M. Approaches to the denominator problem in primary care research[J]. J Fam Pract, 1976, 3(2): 193-195. |
| [24] |
Cherkin DC, Berg AO, Phillips WR. In search of a solution to the primary care denominator problem[J]. J Fam Pract, 1982, 14(2): 301-309. DOI:10.1016/0021-9681(82)90122-9 |
| [25] |
Krogh-Jensen P. The denominator problem[J]. Scand J Prim Health Care, 1983, 1(2): 53. DOI:10.3109/02813438309034933 |
| [26] |
Morrison CN, Rundle AG, Branas CC, et al. The unknown denominator problem in population studies of disease frequency[J]. Spat Spatiotemporal Epidemiol, 2020, 35: 100361. DOI:10.1016/j.sste.2020.100361 |
| [27] |
Vandenbroucke JP, Pearce N. Incidence rates in dynamic populations[J]. Int J Epidemiol, 2012, 41(5): 1472-1479. DOI:10.1093/ije/dys142 |
 2022, Vol. 43
2022, Vol. 43


