在观察性研究中，估计暴露与结局间因果效应的关键是控制混杂。当暴露不随时间变化（time-fixed treatment）时，例如接种疫苗/外科手术等仅在基线发生的处理因素、基因型/性别等不随时间变化的因素、年龄等随时间有确定性变化的因素，采用匹配、分层、回归校正、倾向性评分等传统分析方法即可实现混杂的有效控制。当前，很多大型人群队列研究都试图推断基线暴露与预设的一次随访结局的关系，其中一个常被忽视的假设是基线暴露及其可能的混杂是不随时间变化的。然而在流行病学研究中，许多感兴趣的暴露是随时间变化（time-varying treatment）的，例如药物剂量、用药方案、吸烟状态、空气污染程度、社会经济状态等，此时要估计时变暴露的因果总效应，就必须考虑时依混杂的有效控制。

一、时依混杂

当感兴趣的暴露随时间变化时，可能存在随时间变化的、受过去暴露水平影响并影响着后续暴露水平的混杂，即时依混杂^[1]。例如，在研究抗反转录病毒治疗（anti-retroviral therapy，ART）（X=1为ART，X=0为其他治疗）对HIV感染者的CD4⁺T淋巴细胞（CD4）计数（Y）的影响时（例1），HIV载量（C）为时依混杂（C=1为HIV病毒载量 > 200拷贝/ml，C=0则相反）。在研究起始时受试者的基线HIV病毒载量均 > 200拷贝/ml（C₀=1），而第一次随访时的HIV病毒载量（C₁）会受到研究起始时治疗方案（X₀）的影响，同时其又影响着该次随访时的治疗方案（X₁），成为X₀到Y的一条因果通路上的中介变量（图 1）。此外，当存在同时影响HIV病毒载量（C）和CD4计数（Y）的未测量协变量U₀时，C₁是X₀、U₀和Y因果通路上的对撞因子（collider）（图 1）。在这些复杂情形下，若采用传统分析方法直接控制C₁，很可能产生过度校正偏倚（控制了中介变量C₁）或对撞机偏倚（collider bias，控制了对撞变量C₁），从而无法得到无偏因果效应估计值。

在临床流行病学纵向研究中，许多临床体征或生化指标不仅影响着后续的暴露水平，其本身也受过去暴露水平的影响。例如在研究哮喘抢救药物与呼气流量率峰值（peak expiratory flow rate，PEFR）的因果关系中，某阶段哮喘症状（时依混杂）出现的频率及严重程度与先前用药剂量密切相关，同时也影响着后续用药水平^[2]；在探索他汀类药物对冠心病一级预防效果的研究中，存在受先前是否服用他汀类药物影响的时依混杂，如血清胆固醇水平、DBP值等^[3]；在β受体阻滞剂与急性心梗死亡之间的因果关系研究中，血压值是受先前用药影响的时依混杂^[4]。因此，纵向研究中采用有效的统计方法控制时依混杂是其因果推断的关键。

二、方法和原理

目前发展了3种控制时依混杂的统计方法：参数g-formula、逆概率加权（inverse probability of weighting，IPW）和G估计，统称为G方法。不同于传统方法，G方法不会通过将混杂因素固定在某个值或某个水平而实现控制混杂的目的，因此可有效避免过度校正偏倚和对撞机偏倚，从而得到无偏因果效应估计值^[5]。令X(t)为时变二分类暴露，C(t)为二分类时依混杂，假设C(t)在固定的时间点t=0，…，k处改变，，X(t)={X(0)，…，X(t)}和C(t) = {C(0)，…，C(t)}分别代表每次随访时的暴露状态和混杂水平。

(1) 参数g-formula

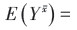
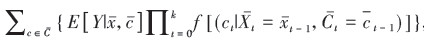
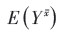
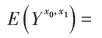
参数g-formula利用了标准化的思想，在多个时间点上构建X、C和Y的联合分布，模拟受试者在暴露和非暴露情况下产生的潜在结果，并估计总体平均潜在结局，例1的可简单表示为：，通过比较暴露组和非暴露组的潜在预期结局估计处理效应^[6-7]。吴诗蓝等^[8]在探究膳食纤维摄入量（fiber≤30 g/d或 > 30 g/d）是否影响冠心病发病风险的纵向研究中，每次随访时糖尿病是否发生既受到过去膳食纤维摄入量的影响，又可能使受试者未来的膳食行为发生改变，是需要控制的时依混杂，采用参数g-formula得到结果为fiber > 30 g/d的人患冠心病的风险是fiber≤30 g/d患病风险的0.86倍（95%CI：0.78~0.99）；而当采用传统回归校正方法时，得到的结果为0.74（95%CI：0.48~1.14），显然其95%CI更宽，更易产生有偏估计结果^[8]。

(2) IPW

在没有未测量混杂（no unmeasured confounding）假设下，给每个观测者分配权重来重新获得一个混杂在组间均衡分布的伪人群，在该人群中拟合处理因素和结局间的边际结构模型（marginal structure models，MSMs）即可得到因果效应无偏估计值^[9-10]。IPW的计算包括不稳定权重：；和稳定权重：（例1中： ）。之所以称为不稳定权重是由于，可能有受试者在X_k-1，C_k条件下被分配进入暴露组的估计概率极低，致其W极大，使因果效应估计量的标准误增大，甚至产生偏倚^[11-12]。SW将分子替换为个体实际接受暴露的边际概率，故基于SW的因果效应估计值标准误显著降低^[11]。Danaei等^[3]在评估他汀类药物在冠心病一级预防中的作用时，使用IPW和MSMs分析，发现服用他汀类药物能够降低冠心病发病风险HR=0.79（95%CI：0.41~1.41），而用传统回归校正方法得到的结论为HR=1.31（95%CI：1.04~1.66），这与RCT试验得到的结论HR=0.72（95%CI：0.65~0.79）相悖^[13]。

(3) G估计

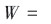
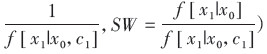
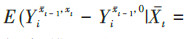
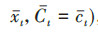
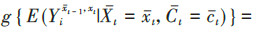
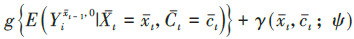
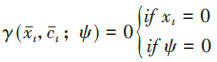
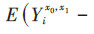
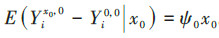
将暴露效应定义为比较同一个体或一组受试者接受暴露和非暴露的潜在结局^{[5, 14]}。首先，在先前暴露状态和混杂水平下，第t次随访暴露与非暴露的效应估计值为，随后采用结构嵌套模型（structural nested mean models，SNMs）来参数化处理组受试者的平均因果效应： ，其中g（.）为链接函数（如identity链接、log链接、logit链接），γ (x_t，c_t；ψ)是波动函数（如线性波动函数），其满足只有ψ是需要估计的未知有限维参数^[15-16]。以例1为例，采用identity链接和线性波动函数，有： 和。根据条件可交换性假设，每个时间点的暴露与结局间的条件协方差为0，则可估计出系数ψ。Shakiba等^[17]在一项量化肥胖和冠心病发病风险间因果关系的研究中使用G估计控制时依混杂（包括发生高血压/糖尿病/脑卒中、血清胆固醇/TG、吸烟饮酒状态），得到腹型肥胖患病风险更高HR=1.65（95%CI：1.35~1.92）的结论，而仅调整了基线混杂的传统Cox回归方法得到的结论为HR=0.93（95%CI：0.77~1.12）。

三、方法比较

本研究将从原理、适用范围、估计的有效性和稳定性、计算复杂程度等方面比较3种方法的差异，并用表 1简要概括了3种方法的优缺点。

(1) 原理

参数g-formula可以看作标准化方法在多个随访时间点的拓展，通过预测缺失的反事实结局，比较在不同的假设干预下人群的结局是否存在差异；IPW通过对调查人群加权，获得一个不受混杂因素影响的、伪随机化的人群^{[1, 18]}。这2种方法是直观的，相对于G估计更好理解，但是通过G估计得到的因果效应结论更容易外推到其他人群中^[18]。

(2) 零悖论

因果推断的零假设为暴露和结局间不存在因果关联，当零假设为真时错误地拒绝零假设被称为零悖论^[19]。参数g-formula需要估计给定协变量和处理因素的平均结局效应E [Y|X = x，C = c]，和给定历史协变量和处理因素时该次随访协变量的分布布f[(C_t = c_t|X_{t- 1} = x_{t- 1}，C_{t- 1} = c_{t- 1})。。当先前的暴露对之后的混杂有非零影响时，基于参数g-formula得到的结论会与零假设不一致，即产生了零悖论^{[1, 18]}。而其他2种估计方法不存在零悖论，零假设对IPW而言，意味着加权后的MSMs中估计的暴露系数为0；零假设在G估计中，对应着波动函数的有限维参数ψ = 0^[18]。因此零悖论也被称为g-null悖论，其只会发生在控制时依混杂的因果推断中。避免零悖论的方法是仅考虑已知对结局有影响的暴露，或基于零假设不成立的先验信息^[20]。

(3) 估计的有效性和稳定性

参数g-formula估计的有效性和稳定性主要依赖于模型是否被正确设定，尤其是在不能排除零假设的前提下，而一旦结局模型（以结局为预测变量建模）和混杂模型（以混杂为预测变量建模）均被正确设定，参数g-formula的效率和稳定性都很高^[18]。基于IPW加权建立伪人群方法的效率和稳定性都低于模型正确设定时的参数g-formula，且随着混杂维数的增加，IPW的变异性增加，会给数据集中少数受试者非常大的权重，导致其低效和不稳定性进一步增加^{[18, 21]}。G估计的效率和稳定性通常介于参数g-formula和IPW之间，与MSMs相比，SNMs可以纳入暴露和混杂的交互项，这可能是G估计的效率高于IPW的原因^[18]。

(4) 适用范围

参数g-formula可用于估计较复杂的联合暴露（例如吸烟和每日≥30 min的体育锻炼对健康的联合效应），但当暴露是连续变量/具有多个水平的分类变量/具有多个随访时间点的二分类变量，且无感兴趣的暴露水平时，参数g-formula要估计每一种可能处理组合的平均结局，当有太多可能的假设处理水平可供比较时，计算量很大，模型解释变得很困难，同时也会增加模型误设的概率^{[1, 18]}。当某一混杂水平下所有受试者均为暴露或均为非暴露，即违背了正性假设（给定的混杂水平下，没有接受某个处理水平概率为零的受试者）时，不能用IPW方法^[1]；IPW难以处理连续性暴露，且由于MSMs是边际的，因此无法纳入暴露和混杂的交互项。G估计可以纳入暴露和混杂的交互项^{[1, 19]}。参数g-formula和IPW均可以用于连续性、分类的结局变量以及生存分析中；G估计在生存分析中采用的模型为基于SNMs的结构嵌套累计失效时间模型^[22]。

上述G方法对随访次数均不做限制，但随着随访次数增加，失访比例可能增大。虽然G方法能够将失访视为另一种可能的治疗方式，从而通过二次加权均衡失访偏倚，但其需要假设失访是完全随机发生的。而在实际研究中，失访常与暴露或结局存在一定关联，因此在设计阶段采取一系列措施提高随访率是十分必要的，例如纳入主动性较高更易跟踪随访的受试者、设计的问卷尽可能易于理解和完成、确保在所有研究小组中保持高水平的随访等。此外，研究者应结合临床实际、文献报道、或进行预调查，判断研究纳入的暴露和协变量是否随时间变化，即判断是否存在需要控制的时依混杂，虽然在理论上G方法可以估计不随时间变化的暴露因素与结局间的因果效应，但其复杂程度要远高于传统的匹配、分层、倾向性评分等方法。本研究仅讨论了包含单个随访时间点结局事件（即随访终点结局事件Y）的因果效应估计，但研究者可根据实际研究问题将G方法拓展到包含了多个随访时间点结局事件（Y_i）的因果效应估计中^[23]。

(5) 计算和程序实现

参数g-formula计算较复杂，因为涉及了蒙特卡洛模拟和bootstrap，可用Stata软件中的“gformula”命令或R软件中的“gformula”软件包实现；IPW可在大多数统计软件中轻松实现，可参考R软件包“ipw”；G估计计算较复杂，可通过Stata软件中的“stgest”命令、SAS软件中的“SURV”宏程序或R软件中的“DTRreg”软件包实现。

四、实例分析

以2016年Naimi等^[5]的研究报告中关于ART治疗对HIV感染者CD4计数影响的前瞻性研究数据为例，比较传统回归分析方法与3种G方法估计效应的准确性（表 2）。该研究调查了基线（t₀）和第一次随访（t₁）时的ART状态，分别用X₀、X₁表示（X_i=1为接受ART、X_i=0为未接受ART）；基线的HIV病毒载量（C₀）均 > 200拷贝/ml，在第一次随访时第二次治疗前测得的HIV病毒载量（C₁）为时依混杂（C₁=0表示≤200拷贝/ml，C₁=1则相反），随访结束时测得的CD4计数（个/μl）为结局Y（因果图可参考图 1）。分别用传统线性回归方法，包括只考虑基线治疗状态X₀和同时考虑两次治疗状态X₀和X₁的校正了C₁的线性回归模型，以及3种可以控制时依混杂C₁的G方法，估计ART与CD4计数间的因果关系。表 2中β₀、β₁分别代表X₀、X₁的回归系数，Δŷ_mean代表基线和第一次随访时均接受ART（X₀=1且X₁=1）与均未接受ART（X₀=0且X₁=0）分别对应的Y均值的差异。表 2中显示，G方法估计的β₀和β₁很接近，即在t₀和t₁时的ART对CD4计数的影响效应相同，而传统回归方法估计的β₀和β₁有较大差异；且G方法估计的Δŷ_mean均为50.0个/μl，即两次均接受ART的患者CD4计数平均增加50.0个/μl。传统回归方法则低估了ART与CD4计数间的因果效应，尤其是在只关注基线暴露对结局的影响效应时。

五、总结

在纵向研究中，常常存在受过去暴露影响的时依混杂，但在实践中，通常被忽略或者直接使用传统方法进行调整，得到有偏因果效应估计值。G方法是在对暴露和混杂进行重复测量的纵向数据中，调整受过去暴露影响的时依混杂的方法。在一项关于2000-2016年控制时依混杂的相关研究文献的系统回顾中，使用G方法的文献虽然在逐年增加，但也仅占总文献量的20%，且其中有60.9%集中在HIV、心肺疾病、肾病或精神健康领域，80.3%采用的方法是IPW^[24]。因此，本研究可为不同领域的研究人员在处理纵向数据的因果推断实践中提供参考，由于G方法包括的3种方法的适用范围、估计的有效性和稳定性有差异，研究者应根据实际情况，选择适合的G方法控制时依混杂，从而获得无偏因果效应估计值。

利益冲突  所有作者均声明不存在利益冲突