文章信息
- 甘秀敏, 赵燕, 马烨, 吴亚松, 赵德才.
- Gan Xiumin, Zhao Yan, Ma Ye, Wu Yasong, Zhao Decai
- 脱落率加权调整在医学重复测量资料敏感性分析中的应用及其SAS程序实现
- Application of weighted adjustments of dropout rates in sensitivity analysis of medical repeated measurements data and implementation with SAS
- 中华流行病学杂志, 2021, 42(6): 1118-1123
- Chinese Journal of Epidemiology, 2021, 42(6): 1118-1123
- http://dx.doi.org/10.3760/cma.j.cn112338-20201217-01414
-
文章历史
收稿日期: 2020-12-17
医学研究中,常需要在不同时点对同一研究对象的同一观察指标进行多次纵向观测,所获得的重复测量资料可用于分析该观察指标在不同时点的变化规律。在长期随访或定期监测过程中,因研究对象主观或客观原因以及受研究设计与实施过程中多方面复杂因素的共同影响,不可避免会出现研究对象脱落、观察指标数据缺失的现象。医学重复测量资料中缺失数据的存在增加了统计分析的复杂性,使结果解释和结论应用存在一定困难,若直接忽略缺失值而采用完整观测分析或有效病例分析方法时,因其舍弃了含缺失数据观测所含的已知信息且不符合意向性分析原则,可能会导致统计分析结果存在偏差甚至错误[1-2]。为了得到更科学的研究结论,以临床试验为例,美国国家研究委员会发布了临床试验中缺失数据的预防和处理措施报告,建议研究者在进行意向性分析以评价主要疗效指标的同时,可采用生成不同人群分析数据集、进行数据填补或建立多种模型等敏感性分析方法进行结果的比较,以辅助验证研究结论的稳定性[3-4]。已有研究表明,作为单一填补法的延伸,目前较常用的多重填补法要求数据符合完全随机缺失或随机缺失假设,当无法确定是否存在偏离上述假设的情况时,可采用选择模型、模式混合模型等建模法进行敏感性分析[3-6],尤其是当组间缺失情况存在差异时,考虑脱落率对研究结果的影响开展敏感性分析是非常有必要的[7]。鉴于此,本研究通过编写SAS程序,以重复测量混合效应模型(mixed-effects models for repeated measures,MMRM)为基础,对医学重复测量资料进行协方差分析,同时构建基于脱落率加权调整的模式混合模型(pattern-mixture models,PMM)以评估脱落对分析结果的影响,为脱落率调整在医学重复测量资料敏感性分析中的应用提供实践依据。
资料与方法1.资料来源和变量赋值:数据来源于多变量医学重复测量资料,本研究截取了前5周数据资料用于开展方法学实践性分析。按照随机、双盲、平行对照的原则,研究将受试者分为三组,即药物治疗低剂量组、药物治疗高剂量组和安慰剂组,组间受试者比例为1∶1∶1。研究过程中每周需对受试者进行一次量表评估,所得评分用以评价疗效指标前后变化情况,研究目的是与安慰剂组相比,观察使用高、低剂量药物后疗效指标较基线改变量之间的差异。见表 1。
2.研究方法:(1)不考虑脱落对试验的影响:通过SAS 9.4软件中混合效应模型MIXED过程构建MMRM将基线后各访视疗效指标测量值与基线的差值作为应变量,将试验分组、访视时间、试验分组*访视时间作为固定效应,将疗效指标基线值作为协变量,受试者为随机效应,采用非结构化协方差矩阵(un-structured covariance matrix),MMRM:
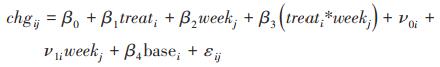
式中,i=1,…,N病例数;j=1,…,M访视数;β0为截距,β1、β2、β3和β4为各自变量及交互相的系数;ν0i和ν1i为随机效应,ε为残差。
(2)考虑脱落对试验的影响:以重复测量协方差分析模型为基础,将基线后各访视疗效指标测量值与基线的差值作为应变量,将试验分组、访视时间、试验分组*访视时间、脱落情况、脱落情况*试验分组、脱落情况*访视时间和脱落情况*试验分组*访视时间作为固定效应,将疗效指标基线作为协变量,受试者为随机效应,采用非结构化协方差矩阵,构建模式混合模型[7-8]:

式中,i = 1, …, N病例数;j = 1, …, M访视数。β0为截距,β1、β2、β3、β4、βd0、βd1、βd2和βd3为各自变量及交互相的系数,ν0i和ν1i为随机效应,ε为残差。三交互项表示药物疗效随着时间和完成试验情况变化而变化。
以样本脱落率作为数据缺失的评估比例,带入模型中估算模式混合的平均结果(pattern-mixture averaged results)[9]:
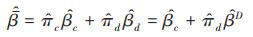
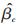
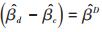
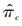
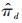
分别采用边际(marginal)脱落率(即总体脱落率)及各组药物自身(drug-specific)脱落率(即各组脱落率),对高、低剂量组与安慰剂组疗效指标较基线改变量之间的差异进行参数估计和统计推断。
采用SAS 9.4软件,SAS程序如下:
① MMRM分析SAS程序:
proc mixed data=dataset;
class subid treat week;
model chg = treat week treat*week base;
repeated week/sub=subid type=un;
lsmeans treat*week / diff cl;
estimate 'group1 vs placebo' treat 1 0 -1;
estimate 'group2 vs placebo' treat 0 1 -1;
run;
② 脱落率加权调整PMM分析SAS程序:
/*赋值宏变量:总体、各组脱落率及各组脱落率差值*/;
%let rall=0.1227;*总体脱落率;
%let rp=0.0877;*安慰剂组脱落率*;
%let rg1=0.1179;*低剂量组脱落率*;
%let rg2=0.1615;*高剂量组脱落率*;
%let dg1=0.0302;*低剂量组与安慰剂组脱落率的差值*;
%let dg2=0.0738;*高剂量组与安慰剂组脱落率的差值*;
proc mixed data= dataset method=reml;
class treat subid;
model diff=week treat week*treat drop drop*week drop*treat drop*week*treat base/solution;
random intercept week/sub=subid type=un g gcorr;
estimate 'week*drop*treat placebo vs. group1'
drop*week*treat 1 0 -1;
estimate 'week*drop*treat placebo vs. group2'
drop*week*treat 0 1 -1;
****marginal intercept;
estimate 'IPA:INT Placebo Average'
intercept 1 treat 0 0 1 drop & rall drop*treat 0 0 & rall;
estimate 'I1AP:INT Group1 over Placebo Average'
treat 1 0 -1 drop*treat & rall 0 - & rall;
estimate 'I2AP:INT Group2 over Placebo Average'
treat 0 1 -1 drop*treat 0 & rall - & rall;
contrast 'I1AP:INT Group1 over Placebo Average'
treat 1 0 -1 drop*treat & rall 0 - & rall;
contrast 'I2AP:INT Group2 over Placebo Average'
treat 0 1 -1 drop*treat 0 & rall - & rall;
contrast 'IbothAP:INT Group1= INT Group2= INT Placebo Average'
treat 1 0 -1 drop*treat & rall 0 - & rall,
treat 0 1 -1 drop*treat 0 & rall - & rall;
****marginal slope;
estimate 'WPA:Week(Slope)Placebo Average'
week 1 Week*treat 0 0 1 drop*week & rall drop*week*treat 0 0 & rall;
estimate 'W1AP:Week(Slope)Group1 over Placebo Average'
week*treat 1 0 -1 drop*week*treat & rall 0 - & rall;
estimate 'W2AP:Week(Slope)Group2 over Placebo Average'
Week*treat 0 1 -1 drop*week*treat 0 & rall - & rall;
contrast 'WbothAP:INT Group1= INT Group2= INT Placebo Average'
week*treat 1 0 -1 drop*week*treat & rall 0 - & rall,
week*treat 0 1 -1 drop*week*treat 0 & rall - & rall;
****by treatment group intercept;
estimate 'T_IPA:INT Placebo Average'/**/
intercept 1 treat 0 0 1 drop & rp drop*treat 0 0 & rp;
estimate 'T_I1AP:INT Group1 over Placebo Average'/**/
treat 1 0 -1 drop & dg1 drop*treat & rg1 0 - & rp;
estimate 'T_I2AP:INT Group2 over Placebo Average'
treat 0 1 -1 drop & dg2 drop*treat 0 & rg2 - & rp;
contrast 'T_IbothAP:INT Group1= INT Group2= INT Placebo Average'
treat 1 0 -1 drop & dg1 drop*treat & rg1 0 - & rp,
treat 0 1 -1 drop & dg2 drop*treat 0 & rg2 - & rp;
****by treatment group slope;
estimate 'T_WPA:Week(Slope)Placebo Average'
week 1 Week*treat 0 0 1 drop*week & rp drop*week*treat 0 0 & rp;
estimate 'T_W2AP:Week(Slope)Group1 over Placebo Average'
week*treat 1 0 -1 drop*week & dg1 drop*week*treat & rg1 0 - & rp;
estimate 'T_W2AP:Week(Slope)Group2 over Placebo Average'
week*treat 0 1 -1 drop*week & dg2 drop*week*treat 0 & rg2 - & rp;
contrast 'T_WbothAP:INT Group1= INT Group2= INT Placebo Average'
week*treat 1 0 -1 drop*week & dg1 drop*week*treat & rg1 0 - & rp,
week*treat 0 1 -1 drop*week & dg2 drop*week*treat 0 & rg2 - & rp;
run;
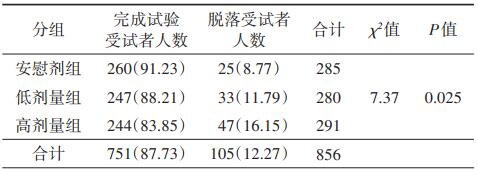
结果1.试验各组脱落情况:将完成5周治疗过程并有第5周主要疗效指标评估的受试者定义为完成病例(drop=0),反之则定义为未完成病例(drop=1),各组受试者脱落情况见表 2。试验总体受试者脱落率为12.27%,安慰剂组、低剂量组和高剂量组的受试者脱落率分别为8.77%、11.79%和16.15%。采用CMH χ2检验对三组受试者脱落率进行比较,三组受试者脱落率之间的差异有统计学意义(χ2=7.37,P=0.025),高剂量组受试者脱落率高于低剂量组和安慰剂组。
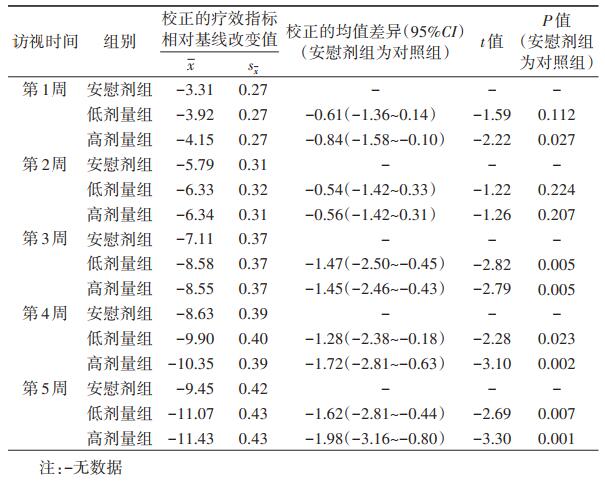
2.不考虑脱落对试验的影响:重复测量混合效应模型总体结果显示,高、低剂量组与安慰剂组疗效指标较基线改变量之间的差异均有统计学意义(P=0.008和P=0.002)。见表 3。各访视高、低剂量组与安慰剂组疗效指标较基线改变量比较结果表明,在第1周和第2周,低剂量组与安慰剂组疗效指标较基线改变量之间的差异无统计学意义(P > 0.05);从第3周开始,低剂量组与安慰剂组疗效指标较基线改变量之间的差异均有统计学意义(P < 0.05);除第2周外,其他访视时间高剂量组与安慰剂组疗效指标较基线改变量之间的差异均有统计学意义(P < 0.05)。见表 4。
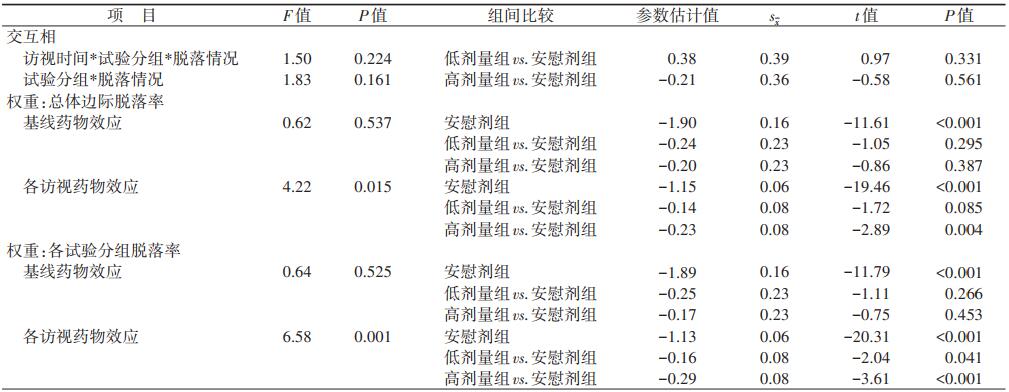
3.考虑脱落对试验的影响:分别引入试验总体和各试验组脱落率的模式混合模型结果。见表 5。引入试验总体边际脱落率的敏感性分析结果显示,低剂量组与安慰剂组疗效指标较基线改变量之间的差异无统计学意义(P=0.085),高剂量组与安慰剂组疗效指标较基线改变量之间的差异有统计学意义(P=0.004)。引入各试验组脱落率的敏感性分析结果显示,高、低剂量组与安慰剂组疗效指标较基线改变量之间的差异均有统计学意义(P=0.041和P < 0.001)。
数据缺失的发生在真实世界医学重复测量资料获得过程中往往是无法避免的,如何合理选择数据处理和分析方法,充分利用现有研究资料、客观评估样本分析结果进而合理推断总体研究结论,一直备受国内外学者们的关注。Little等[9]和Rubin等[10]曾系统阐述了有关缺失数据的有关问题,包括数据缺失机制和相应的参数估计方法等。根据数据缺失产生的原因,可将缺失数据大致分为三类,即应变量的缺失完全是由随机因素引起的完全随机缺失(missing completely at random,MCAR)数据、应变量的缺失仅与已观测到的应变量值有关的随机缺失(missing at random,MAR)数据和应变量的缺失不仅与已观测到的应变量值有关且还可能与未观测到的应变量值有关的非随机缺失(missing not at random,MNAR)数据。MCAR数据可被视为研究总体中的一个随机样本,可采用常规统计分析方法进行分析,但往往在实际研究过程中所获得的医学重复测量资料较难满足证实MCAR数据繁多严苛的前提条件[11-12],真实世界中MAR数据和MNAR数据更为常见。
对于存在缺失数据的医学重复测量资料,一般都需要进行敏感性分析已验证结论的稳健性,主要可采用两种方法进行处理。一是填补法,即先对数据进行填补,再对填补后的数据进行统计分析,如单一填补法和目前常用的多重填补法(multiple imputation)等,后者是前者的延伸,较适用于MCAR数据和MAR数据[1-2, 13],而当缺失数据无法排除MNAR的可能时,多重填补法在处理MNAR数据时较难得到无偏的参数估计值;二是非填补法,即通过生成不同人群分析数据集或建立多种模型的方法直接对数据进行统计分析。已有研究认为,MMRM建模具有较大灵活性,该模型可在不剔除存在缺失数据的研究对象或不进行缺失数据填补的情况下,充分利用已观测到的应变量信息获得有效的参数估计和统计推断[5, 12];PMM建模可将缺失模式引入随机效应变量,根据缺失模式出现概率得到不同缺失模式下各参数的偏差大小,有效估计出由于MNAR所导致的结果偏倚。PMM建模时不限制数据缺失机制的具体分布形式,不仅适用于多种缺失机制的数据,尤其对于MNAR数据,使用该模型进行参数估计时更加稳健,因此建议将PMM作为偏离MAR假设时敏感性分析方法之一[13-16]。
鉴于此,针对存在数据缺失且各组脱落率之间的差异存在统计学意义的医学重复测量资料,本研究在MMRM建模得到主要疗效指标分析结果的基础上,引入了脱落率变量,分别采用总体脱落率和各组自身脱落率作为权重,构建了基于脱落率加权调整的PMM进行敏感性分析,以实现校正脱落率对试验结果的影响、进一步验证结果稳健性的目的。本研究中三组脱落率之间的差异有统计学意义,高剂量组脱落率高于低剂量组和安慰剂组,故考虑脱落率对试验结果的影响是非常必要的。因各组脱落率之间的差异有统计学意义,故应采用各组自身脱落率调整的PMM结果,高、低剂量组与安慰剂组疗效指标较基线改变量之间的差异均有统计学意义,以各组自身脱落率作为权重进行校正后的PMM敏感性分析结果与MMRM模型一致。若敏感性分析结果与主要分析结果不一致,则表明数据缺失对研究结果产生了一定的影响,则需要更进一步对数据进行挖掘,根据数据缺失产生原因深入分析其对疗效指标的影响,或采用亚组分析等方式来进一步探讨导致结果不一致的具体原因。
综上所述,真实世界研究中发生数据缺失是我们认识事物真实发展规律的较大阻碍,在研究设计阶段、实施和统计分析等一系列研究过程中都应充分考虑数据缺失的可能性并明确相应的处理措施。在研究设计阶段,应确定各类分析人群数据集的定义和缺失数据处理方法;在研究实施阶段,应尽可能降低数据缺失发生的概率,获得更为准确的第一手真实数据;在数据统计分析阶段,应严格按照统计分析计划,运用丰富的专业背景知识,针对数据收集阶段数据缺失产生的原因进行详细分析和判断。当数据缺失原因的详细信息难以获得、无法准确判断数据缺失机制,且各组脱落率之间的差异有统计学意义时,可在应用MMRM建模分析的基础上,选择加权调整脱落率的PMM建模方法进行敏感性分析,以验证结论的可靠性。本研究所提供的SAS程序也可为该方法的推广和应用提供实践参考。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
鲍晓蕾, 高辉, 胡良平. 多种填补方法在纵向缺失数据中的比较研究[J]. 中国卫生统计, 2016, 33(1): 45-48. Bao XL, Gao H, Hu LP. Comparative study of various imputation methods in dealing with longitudinal missing data[J]. Chin J Health Stat, 2016, 33(1): 45-48. |
| [2] |
帅平, 李晓松, 周晓华, 等. 缺失数据统计处理方法的研究进展[J]. 中国卫生统计, 2013, 30(1): 135-139, 142. Shuai P, Li XS, Zhou XH, et al. Research progress of statistical processing methods for missing data[J]. Chin J Health Stat, 2013, 30(1): 135-139, 142. |
| [3] |
Little RJ, D'Agostino R, Cohen ML, et al. The prevention and treatment of missing data in clinical trials[J]. N Engl J Med, 2012, 367(14): 1355-1360. DOI:10.1056/NEJMsr1203730 |
| [4] |
王骏, 韩景静, 黄钦. 临床试验缺失数据的统计学考量[J]. 中国临床药理学杂志, 2016, 32(5): 469-472. Wang J, Han JJ, Huang Q. Statistical considerations on missing data in clinical trials[J]. Chin J Clin Pharmacol, 2016, 32(5): 469-472. DOI:10.13699/j.cnki.1001-6821.2016.05.027 |
| [5] |
吴秋红, 张裕青, 李国平, 等. 不同模型处理纵向缺失数据的模拟研究及应用[J]. 中国卫生统计, 2013, 30(6): 855-858, 861. Wu QH, Zhang YQ, Li GP, et al. Simulation research and application of different models in processing longitudinal missing data[J]. Chin J Health Stat, 2013, 30(6): 855-858, 861. |
| [6] |
Daniels MJ, Jackson D, Feng W, et al. Pattern mixture models for the analysis of repeated attempt designs[J]. Biometrics, 2015, 71(4): 1160-1167. DOI:10.1111/biom.12353 |
| [7] |
Hedeker D, Gibbons RD. Application of random-effects pattern-mixture models for missing data in longitudinal studies[J]. Psychol Methods, 1997, 2(1): 64-78. DOI:10.1037/1082-989X.2.1.64 |
| [8] |
Hedeker D, Gibbons RD. Longitudinal data analysis[M]. New York: Wiley, 2006.
|
| [9] |
Little RJA, Wang YX. Pattern-mixture models for multivariate incomplete data with covariates[J]. Biometrics, 1996, 52(1): 98-111. DOI:10.2307/2533148 |
| [10] |
Rubin DB. Inference and missing data[J]. Biometrika, 1976, 63(3): 581-592. DOI:10.1093/biomet/63.3.581 |
| [11] |
金勇进, 邵军. 缺失数据的统计处理[M]. 北京: 中国统计出版社, 2009. Jin YJ, Shao J. Statistical processing of missing data[M]. Beijing: China Statistics Press, 2009. |
| [12] |
陈丽嫦, 衡明莉, 王骏, 等. 定量纵向数据缺失值处理方法的模拟比较研究[J]. 中国卫生统计, 2020, 37(3): 384-388. Chen LC, Heng ML, Wang J, et al. Missing data handing methods of quantitative longitudinal data: a simula-tion study[J]. Chin J Health Stat, 2020, 37(3): 384-388. |
| [13] |
江震, 斗智, 宋炜路, 等. MSM人群HIV感染者病毒载量抽样调查缺失数据填补方法研究[J]. 中华流行病学杂志, 2017, 38(11): 1563-1568. Jiang Z, Dou Z, Song WL, et al. Comparison of different methods in dealing with HIV viral load data with diversified missing value mechanism on HIV positive MSM[J]. Chin J Epidemiol, 2017, 38(11): 1563-1568. DOI:10.3760/cma.j.issn.0254-6450.2017.11.025 |
| [14] |
Bunouf P, Molenberghs G. Implementation of pattern-mixture models in randomized clinical trials[J]. Pharm Stat, 2016, 15(6): 494-506. DOI:10.1002/pst.1780 |
| [15] |
Moreno-Betancur M, Chavance M. Sensitivity analysis of incomplete longitudinal data departing from the missing at random assumption: methodology and application in a clinical trial with drop-outs[J]. Stat Methods Med Res, 2016, 25(4): 1471-1489. DOI:10.1177/0962280213490014 |
| [16] |
Fiero MH, Hsu CH, Bell ML. A pattern-mixture model approach for handling missing continuous outcome data in longitudinal cluster randomized trials[J]. Stat Med, 2017, 36(26): 4094-4105. DOI:10.1002/sim.7418 |
 2021, Vol. 42
2021, Vol. 42