文章信息
- 肖燕妮, 李倩, 周伟柯, 彭志行, 唐三一.
- Xiao Yanni, Li Qian, Zhou Weike, Peng Zhihang, Tang Sanyi
- 新型冠状病毒肺炎疫情多次暴发的动力学机制分析
- Analysis on dynamical mechanism of multi outbreaks of COVID-19
- 中华流行病学杂志, 2021, 42(6): 966-976
- Chinese Journal of Epidemiology, 2021, 42(6): 966-976
- http://dx.doi.org/10.3760/cma.j.cn112338-20210219-00123
-
文章历史
收稿日期: 2021-02-19
2. 陕西师范大学数学与统计学院, 西安 710019;
3. 南京医科大学公共卫生学院 211166
2. School of Mathematics and Statistics, Shaanxi Normal University, Xi'an 710019, China;
3. School of Public Health, Nanjing Medical University, Nanjing 211166, China
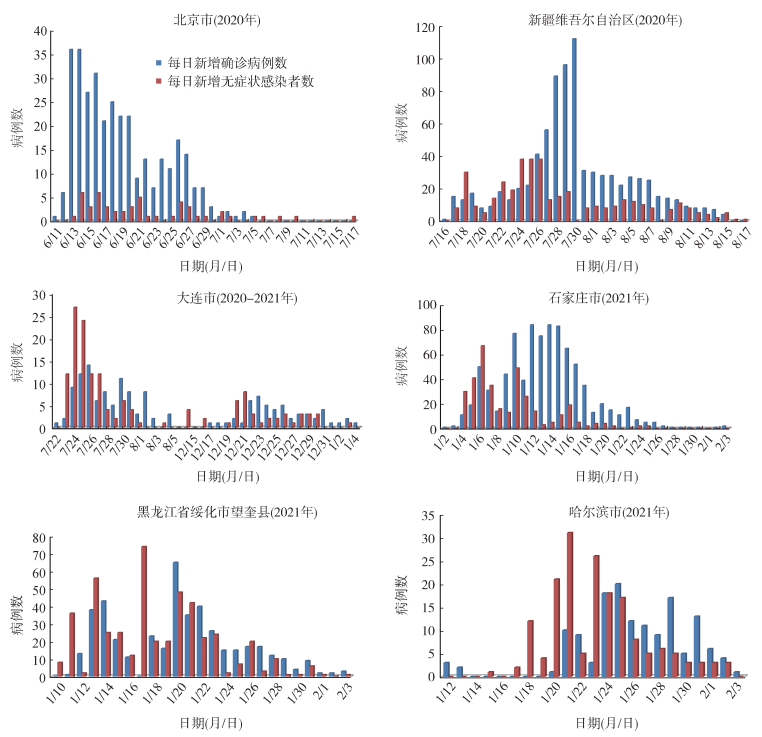
新型冠状病毒肺炎(新冠肺炎)疫情已在世界各地蔓延。2020年末,海外疫情加剧,特别是在英国、巴西、南非等国家发现的新型冠状病毒(新冠病毒)变异株,传染性更强、致病率和致死率均提高[1-2]。在我国部分地区疫情出现了一定程度集聚性散发,在新疆维吾尔自治区、辽宁省、河北省、黑龙江省等地区相继发生了不同规模的本土聚集性病例(图 1),并且出现了超级传播病例[3]。随着国外病毒变异株的出现,加之境外输入病例的不断增加,同时隔离期后出现阳性的情况和无症状感染者数量的增加等因素给疫情防控带来了极大的挑战。很多国家和地区疫情经历了暴发、防控、二次暴发、再防控的多个波峰的传播模式,我国香港地区经历了明显的3个波峰,日本正在经历较大的第三波新冠肺炎疫情传播,美国的疫情则持续不断的发展恶化[4]。较早的解除防控措施使得疫情的下降趋势可能再次逆转,长时间疫情防控模式下,人们对疫情认知的疲劳,特别是人们自发改变减小感染风险的行为也将随着疫情的多次暴发出现很大变化。令人振奋的是疫苗的投入使用有效保护易感人群,从而阻滞新冠病毒传播,然而目前疫苗接种下的解除措施、新冠病毒的持续变异和疫苗的有限性等给未来疫情防控带来了较大的不确定性。特别是在防止疫情二次暴发的前提下,如何设计优化的解封与疫苗接种策略近期得到了广泛的关注和研究[5-7]。
|
| 注:大连市两次暴发时间分别为2020年7月22日至8月5日、12月15日至2021年1月6日 图 1 我国新型冠状病毒肺炎第一波疫情清零后的部分地区疫情与二次暴发疫情 |
由此可见,引发疫情反复多次暴发的因素众多,有较强的随机性和不可预测性。如何刻画新冠肺炎疫情多次暴发的内在机制、揭示易感人群规模、病毒传播能力、防控措施强弱、个体行为变化和疫苗接种速率与时效性等因素的交叉融合,研究疫情的多次暴发具有挑战性。为此,本研究针对公共卫生领域关键热点问题:①如何构建动态方程刻画人群对新冠肺炎疫情的敏感性,模拟感染者人数驱动的人群行为动态改变率,从而精确描述疫情与行为相互驱动进而导致疫情多次暴发的内在机制?②基于易感人群规模阈值[8],如何确定最优的非药物干预措施力度、最优的疫苗接种覆盖率,如何融合疫苗接种和逐步解除非药物干预措施以便能长时间避免疫情的多次暴发?本研究在经典Susceptible exposed infectious recovered(SEIR)传染病动力学模型框架下,融入非药物干预措施和疫苗接种等因素,推导刻画感染者人数驱动的人群行为动态演化方程[9],通过分析和数值研究揭示新冠肺炎疫情发生多峰传播的机制和本质,研究最优的干预措施和疫苗接种速率来优化非药物措施退出机制,从而有效的避免疫情的多次暴发。
一、方法1.模型构建:融合干预措施以及由感染者驱动的个体行为改变和疫苗接种等多因素,结合经典的SEIR模型,推导本文需要采用的数学模型[9]。考虑人群面对新发或重大传染病时,将自发改变其行为以减小感染风险,易感人群(S)分为两类:行为正常的易感人群和行为发生改变的易感人群。由于易感者被感染后关联的潜伏者未出现症状,因此,潜伏者与易感者视为行为相同,将其分为行为正常的潜伏人群和行为发生改变的潜伏人群。经典的SEIR疾病传播动力学模型公式:
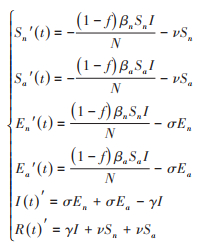 (*)
(*)
模型(*)中将自然传播过程的人群分为易感者类(S)、潜伏者类(E)、感染者类(I)和恢复者类(R)。为分析局部疫情和常态化管理强度,在模型中融入免疫接种(接种率为)和干预措施(干预强度为)等因素。和分别是正常行为和行为发生改变后的传染率,满足,从潜伏类到感染类的转化率为,感染者的康复率为γ。
为了刻画人群行为改变的动态过程,假设个体感知到的感染风险是患病人数的线性函数,即假设易感者保持正常行为和改变行为的收益(收益为代价取负数)分别为:
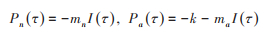
其中mn, ma分别表示正常行为和行为改变的个体由于当前时刻的患病人数而感知到的被感染风险参数,且满足mn > ma, k为行为改变的个体付出的额外代价。个体是否改变其行为可看作是两种决策的博弈。采取一种决策的个体与采取另一决策的个体沟通交流,对两种决策的感染风险进行比较,权衡其成本效益,而后决定是否改变其决策。记ΔP=Pn-Pa,则当Pn>Pa即ΔP>0时,Sa(或Ea)中个体将恢复正常行为成为Sn(或En),反之,当Pn < Pa即ΔP < 0时Sn(或En)中个体将改变其行为成为Sa (或Ea),因此行为改变的动力学方程可以描述为[6]:
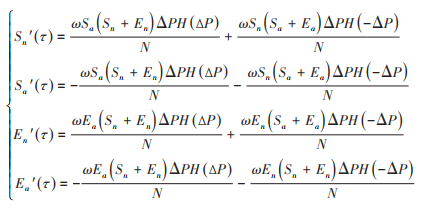 (**)
(**)
其中τ表示行为改变的时间单位,由于感染只会发生在物理接触时,而人与人交流沟通可通过网络电话等进行从而更加频繁,因此,(**)相对(*)是一个快系统,假设t=ατ, α是一个尺度参数,ω是个体间相互沟通并改变决策的率参数,H表示Heaviside函数,即当ΔP≥0时有H(ΔP)=1和当P < 0时有H(ΔP) = 0。相应的考虑人群自发行为改变的传染病动力学模型为疾病传播动力学模型(*)和行为改变模型(**)的耦合,即:
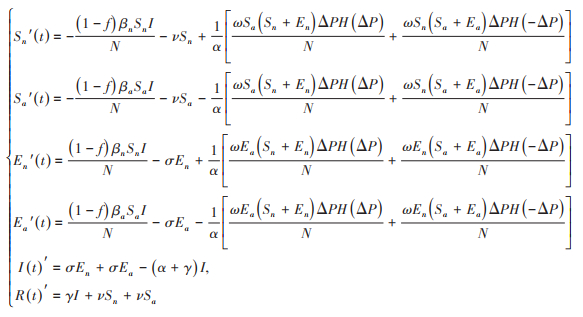 (***)
(***)
p=(Sn+En)/(S+E)表示易感者和潜伏者中保持正常行为的人的比例,其中S=Sn+Sa和E=En+Ea,则当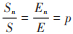
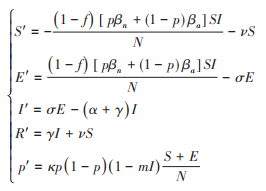 (1)
(1)
其中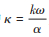
模型(1)中的最后一个方程说明了在新冠病毒感染人数(疫情)的驱动下,个体的行为会在系统的两个稳态0~1之间相互转换(初值选取在0~1之间),而这种切换的快慢由个体对新冠肺炎疫情的敏感程度(即参数)和个体的反应速率(即参数)决定。
2.有效再生数、感染规模和数值分析:当所有的易感个体在疾病暴发期间行为不发生任何变化,即p=1时,根据经典的SEIR模型的主要结论得到相应的基本再生数为:
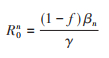
而当所有的易感个体在疾病暴发期间其行为都发生变化,即p=0,则模型的基本再生数为:
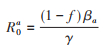
当考虑个体行为随着疫情的演化而动态变化时的完整模型(1),由于行为的变化率和易感人群规模的动态变化,考虑有效再生数R0(t),即为2个特殊系统的基本再生数和关于行为变化率的线性组合:
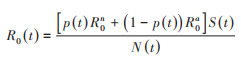
为分析干预措施对包括最终感染规模等在内的关键指标的影响,首先假设行为变化率p是一个常数,不依赖于模型(1)的最后那个微分方程,接种率v=0。记最终感染规模(final size)为F1,则根据分析经典SEIR模型最终感染规模相同的方法,得到表达式:
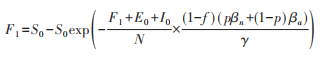
其中初值S0 = S(0),E0 = E(0),I0 = I (0),R0 = R(0) = 0。由F1 = S0 - S∞可得S∞(最终易感人群规模)的表达式为:
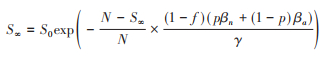
进一步E∞ = I∞ = 0,易证,因此可得R∞ = N - S∞。令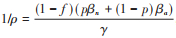
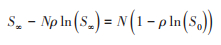 (2)
(2)
根据Lambert W函数的定义和性质,能够确定S∞满足如下的解析公式[10]:
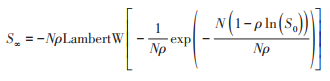
有效再生数是一个与易感人群规模相关的函数,假设当易感人群规模下降到阈值时,有效再生数变为1,即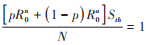
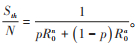
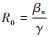
|
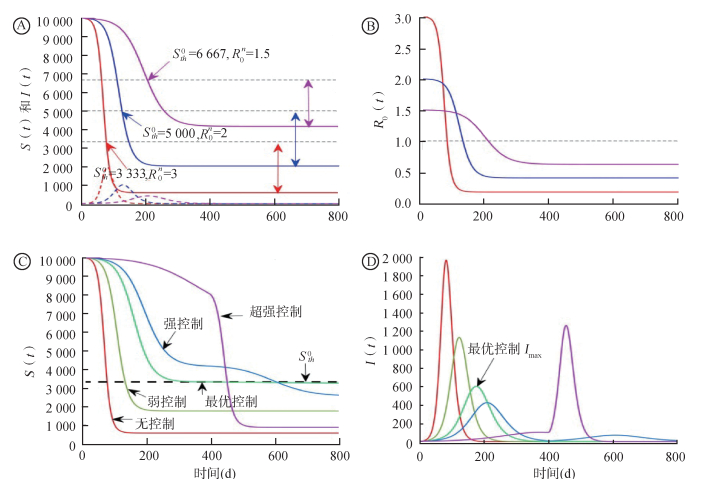
| 注:经典的SEIR模型在给定人口规模为1万时,参数f=0,p=1和ν=0时;A.基本再生数R0分别取值为1.5、2、3时,最终感染规模和易感人群阈值Sth0的关系;B.相应的有效再生数;C和D.基本再生数R0=3以及p=1时,取f = 0、0.3、0.450 9、0.5和0.6分别表示无、弱、最优、强和超强干预措施后的数值实现,其中fc=0.450 9,Sth0=3 333.3,在T=400 d完全解除干预 图 2 经典的SEIR模型在完全自然条件下的解和有效再生数的数值实现 |
为利用模型说明干预措施的强弱对新冠肺炎单波或多波疫情发生的影响,以及免疫接种和个体行为改变如何影响疫情发展,固定基准参数,并采用相应的数值分析方法:总人口规模固定为N=1万,潜伏期时长为5 d(即σ=1/5,治疗时长为10 d(即康复率γ=1/10)。行为改变后的基本再生数R0a=1.5(则相对于f = 0有βa = 0.15),而未发生行为改变时的基本再生数依据文献设定范围为R0n= 1.5~6.5(则相对于f=0有βn=0.15~0.65)[11-19]。若非特别说明,固定k=4,取f = 0、0.3、0.450 9、0.5和0.6,分别表示无、弱、最优、强和超强的干预措施(最优干预措施的计算公式下面一节给出)。“无”指疾病在自然状态下传播,没有受到外界干预措施的影响;“超强干预”指如我国采取的包括密切跟踪隔离、强化检测监测等强有力的防控措施;而“弱、最优和强干预”指介于无和超强干预之间的不同干预强度。通常采用其对传染率的影响大小来刻画,即模型中的参数f。
同时在数值计算时选择不同的v和m来分析不同的疫苗覆盖率和个体对疾病诱导行为改变的敏感性对疫情多波峰暴发的影响,以此分析多波疫情发生的多因素和协同关系。初始值的选取,如不考虑个体行为改变时,模型初值设定为[9 995,0,5,0,1];如考虑个体行为的动态变化时,模型的初值设定为[9 995,0,5,0,0.99],疾病开始时,个体发生行为改变的概率非常小。当分析防控措施在第T天完全解除(即干预措施的强度f=0和系统暴发二次疫情的风险时,需考虑因突发或意外因素在第T天有1个感染者输入的情况。分析在干预措施的强度f=0的疫苗接种对二次暴发的影响时,假设在防控措施完全解除前1周,开始以速率vS接种疫苗(即接种疫苗开始的时间为第T-7天)。数据分析和模型数值计算均运用Matlab 2010软件完成。
二、结果经典的SEIR模型如图 2A、B所示的数值实现,揭示了新冠肺炎疫情在自然状态下演化的基本规律:如果新冠病毒传播能力强(基本再生数大),则易感者最终稳定规模S∞和易感者规模阈值Sth0小,感染者峰值高且出现得早;相反,如果新冠病毒传播能力弱(基本再生数小),则易感者最终稳定规模S∞和易感者规模阈值Sth0大,感染者峰值低且出现较晚。特别是易感者规模下降到阈值Sth0时感染者数量恰好到达高峰Imax。
1.最优的早期干预措施强度与二次暴发风险:首先分析仅有强化干预措施时,如何设计参数使得新冠肺炎疫情得到最佳的防控效果(易感人群规模达到其阈值)。为此,假设行为改变率p=1和v=1,此时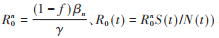
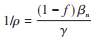
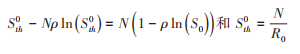
代入相关参数求解得到临界值fc,需满足等式:
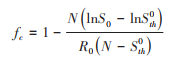 (3)
(3)
该阈值fc的存在揭示了如果疫情早期选择最优的防控措施,后期的输入病例不能引起疫情的二次暴发,也暗示解除超强或强的干预措施的时间过早(即易感者人数 > 易感者规模阈值Sth0的时间之前),则外来流入的病例或突发事件即可导致疫情的二次暴发。见图 2C和D。
为进一步说明干预措施的强弱和逐步解除,对新冠肺炎疫情的严重程度以及二次暴发的关系[5],固定参数值录用,如图 2C和D所示,利用公式(3)计算得到fc= 0.450 9, 进而选择f=0,0.3,0.450 9,0.5和0.6分别表示无、弱、最优、强和超强干预措施,而且按照设计分析干预措施在第400天完全解除(即干预措施的强度降为f=0,并新增1个感染者后继续运行模型到第800天。图 2C和D给出了不同控制条件下的易感者和感染者动态变化的曲线,在无控制或弱控制下,感染者的快速增加导致易感人数快速下降并最终稳定在水平上,其数值小于阈值Sth0。因此,即使在T=400 d由于突发事件输入一例病例对疫情的影响基本可以忽略不计(图 2C和D)。相反,相应于强干预或超强干预措施下的动态变化曲线揭示了过早的解除干预措施,会不同程度地导致新冠肺炎疫情的二次暴发,而且是早期控制措施越强,二次暴发的程度越大。特别的,最优的早期干预措施不仅可以避免后期疫情的二次暴发,更能有效地降低第一波疫情的峰值并推迟其到来的时间(图 2C和D中的绿色曲线)。
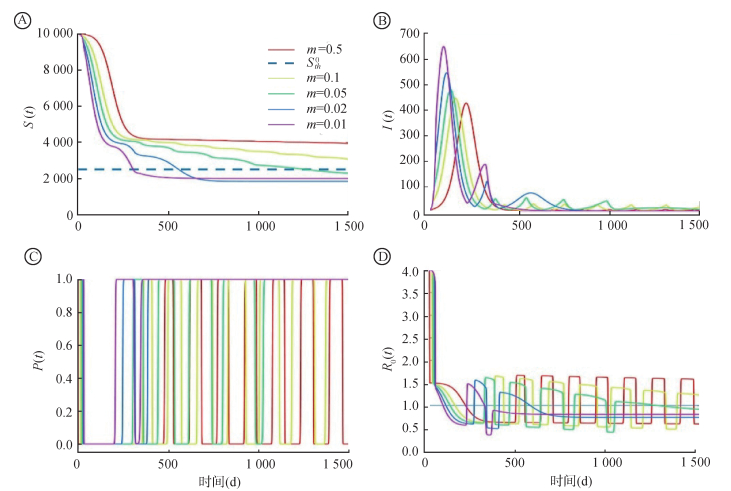
2.个体行为动态演化与二次暴发风险:模型(1)中的个体行为改变率p在疫情的驱动下满足一个微分方程,而反过来个体的行为变化又降低传染的发生率。由此可见感染者的数量与易感者、潜伏类的行为变化之间的相互作用关系,必将导致新冠肺炎疫情发生复杂的动态演化,这为揭示常态化防控策略下的疫情演化具有实际指导意义。为分析上述关系对新冠肺炎疫情的影响,设定人口规模为1万时,固定基本再生数R0=4以及f=0和v= 0,并取m = 0.5,0.1,0.05,0.02和0.01分别表示易感者和潜伏类个体对疫情的超强敏感、强敏感、敏感、弱敏感和不敏感,此时Sth0=2 500。见图 3。
|
| 注:设定人口规模为1万时,固定基本再生数R0 =4以及f=0和v = 0,并取m = 0.5、0.1、0.05、0.02和0.01分别表示易感者和潜伏类个体对感染数量的超强敏感、强敏感、敏感、弱敏感和不敏感时的数值实现,此时Sth0 =2 500 图 3 经典的SEIR模型在易感者和潜伏类个体对感染数量的不同敏感程度的数值实现 |
常态化防控措施下,由于疫情持续时间长、个体行为切换疲劳等因素,导致感染者数量驱动个体行为选择和改变的敏感性程度对疫情的多次暴发具有重要影响。超强的敏感性(m = 0.5)说明个体在区域内有超过2例病例时,就选择改变其行为并加强个人防护,这样将有效地延迟疫情高峰并降低峰值(图 3B),但是易感人群规模始终位于Sth0之上,这不仅导致疫情非常小规模的多次暴发,也使个体行为在两个稳态0~1之间快速切换,从而有效再生数发生较大幅度的高频振动(图 3A、C和D红色曲线)。随着敏感性的降低,个体行为在两个稳态0~1之间快速切换频率逐步降低,有效再生数发生振动的频率和振幅逐渐减小,但是疫情多次暴发的强度不断增大。最后,如果当感染者数量超过100人,个体才选择改变其行为(m = 0.01),发现新冠肺炎疫情在发生大规模的第一波疫情后,紧接着发生较大规模的第二波疫情,致使易感者规模降到阈值Sth0之下而使得疾病逐渐消除(图 3紫色曲线)。这说明对疫情高敏感性(m越大)尽管使得易感人群规模很长一段时间都位于阈值Sth0水平之上,即使后期有可能出现二次暴发,但个体的行为改变能有效压制暴发程度。因此,在无疫苗或接种速度较慢的情况下,高质量的常态化干预和个体的良好依从性以及敏感性是抑制疫情非常重要的措施。
3.疫苗接种与优化常态化防控:前两节分析的是解除强干预措施以及个体行为改变对感染者的敏感程度是诱导疫情多次暴发的重要因素。为了恢复正常生活,强干预措施不可能始终实施,个体也由于防控意识疲劳、工作所需等也不可能对疫情长期处于高度敏感状态。因此,疫苗的研发成功和有效接种是弥补上述缺陷的关键。
与分析强干预措施一样,当仅基于疫苗接种防控新冠肺炎时,为了防止疫情反弹,有意义的问题是:能否确定最佳接种时长或最佳接种率?由于模型(1)的复杂性,直接分析模型来回答该问题挑战性大。为此,首先考虑当接种速率为v时,在什么条件下易感人群规模在T0时刻,能从数量S0T降到易感人群阈值水平Sth0。考虑简单的方程S '=-vS,求解该方程得到S(t) = ST0e-v(t-T0),并假设在T1时刻易感人群数量下降到阈值水平Sth0,则公式:
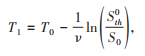 (4)
(4)
即如果从T0以速率v接种易感人群,当考虑疾病传播的同时,那么在T1时刻易感人群数量必定降到Sth0以下,进而达到通过以速率v接种易感人群,在T1时间后就能避免新冠肺炎的二次暴发的目的。
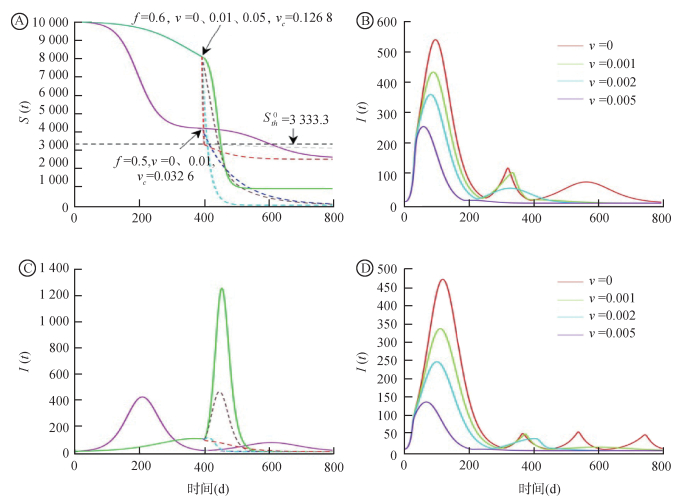
根据图 4A和B所示的强和超强干预措施对应的结果,如果在T1=400 d时解除干预措施(即此后f=0),那么为了避免解除强干预措施后各种因素导致的二次暴发,假设在解除之前的1周开始接种疫苗(即T0=339 d,也可以是2周或更早时间),为了保证在T1时刻后不发生二次暴发,则依据公式(4)最佳的接种率可以根据下式计算:
|
| 注:设定人口规模为1万,固定基本再生数R0=3以及p=1,并取f=0.5和0.6分别表示强和超强干预措施后优化接种疫苗的数值实现;A和B. f=0.5,v=0、0.01和vc=0.032 6;f=0.6,v=0、0.01、0.05和vc=0.126 8;C和D. f=0,m=0.02(0.05),v=0、0.001、0.002、0.005(0.003) 图 4 经典的SEIR模型在强和超强干预措施后优化接种疫苗的数值实现 |
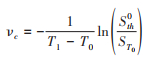
当f=0.5时,通过计算得到Sth0=3333.3,ST0 = 4188.8,vc=0.0326,即当干预措施的强度为强干预时,在解除干预措施之前接种1周的疫苗,且接种率为0.0326就能避免二次暴发(图 4A和B的灰色曲线);当f=0.6时,计算得到Sth0=3333.3,ST0=8096.4,vc=0.1268,即当干预措施的强度为超强干预时,在解除之前接种1周的疫苗,且接种率需要提升到0.1268才能实现目标(图 4A和B的红色曲线)。因此,实施防控措施越强的地区,在解除防控措施之前,为避免更大的二次暴发,就必须让疫苗的接种比例更大。
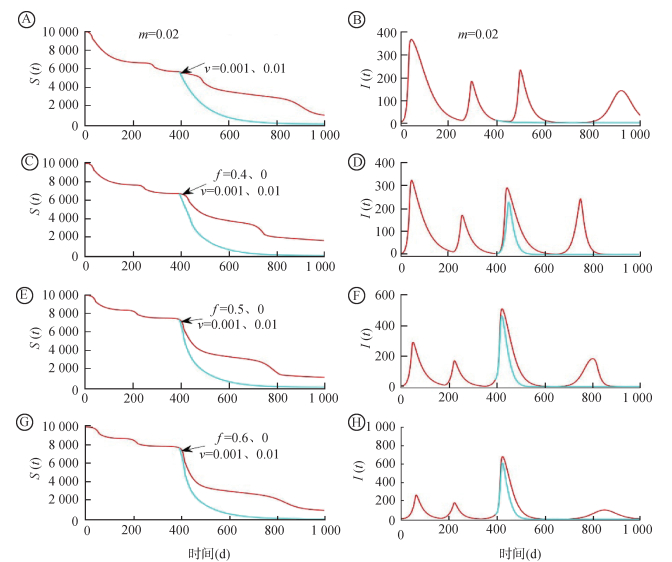
4.强干预措施下疫情诱导的行为改变与疫情的多次暴发:考虑干预措施、民众行为动态变化与免疫接种3个策略的协同优化效应对新冠肺炎疫情的影响。固定参数值见图 5,考虑民众对疫情相同敏感性下干预强度与接种率对疫情多次暴发的影响。比较图 5B、D、F和H的红色曲线,发现:①干预措施持续存在时,相对较弱的干预措施会导致相对较强的第一波疫情、较弱的第二波疫情,且第一波疫情随着干预措施的加强不断减弱;②干预措施解除之后,原来较弱的干预措施会产生相对较弱的第三波疫情,且第三波疫情随着原来干预措施的加强不断增强。为分析疫苗接种与解除干预措施对疫情影响的协调作用,在解除干预措施的前1周提高了接种率,发现相同的接种率对于补偿干预措施解除的效果差异很大(图 5中蓝色曲线)。因此,对于相对较弱的防控措施(f = 0.3),解除其之前1周增加接种率v=1,能够有效抑制疫情的二次暴发。这是由于解除措施时易感人群规模相对较低(图 5B)。然而,解除相对较强的干预措施,再增加同样的接种率的情况下,尽管不能抑制下一波疫情的暴发,但能避免后期的反复多波疫情的发生。见图 5D、F和H。
|
| 注:设定人口规模为1万,固定基本再生数R0 =6,f=0.3、0.4、0.5和0.6,同时考虑个体行为变化与疫苗接种等多因素协同效应时的数值实现。同样在第400天解除干预措施,其中f≠0和v=0.001对应的是红色曲线,f=0和v=0.01对应的是蓝色曲线 图 5 经典的SEIR模型同时考虑个体行为变化与疫苗接种等多因素协同效应时的数值实现 |
疫苗大幅度推广后,2021年2月初世界各国的感染人数开始出现下降,这可能是疫苗的作用初现,或者和近期民众的日常行为有关(很多国家再次采取强有力的防控措施、结束了新年假期或民众开始戴口罩和保持社交距离)。在疫苗接种的持续推进、行为改变的敏感度疲劳作用等情况下,如何制定合理的干预措施缓解方案是疫情控制的关键,还需考虑如何有效融合疫苗接种、民众的行为改变与逐步解除的干预措施等因素,从而最有效地降低疫情多次暴发风险是当前公共卫生面临的核心问题。近期的相关文献就疫苗接种期间保持社交距离的重要性以及如何设计优化的免疫策略[5-6]、免疫策略与干预措施放缓之间的复杂动态关系等进行了系统研究[7],但这些研究不仅忽略了个体行为与疫情共演化是驱动疫情多次暴发的这一关键因素,并没有从本质上就诱导疫情多次暴发的机制进行深入探讨。本研究从数学模型上创新性的提出刻画感染人数驱动的民众行为改变的动态演化,再将疫苗接种、非药物干预措施耦合到经典的SEIR传染病动力学模型中,分析疫情的暴发峰值、最终规模、有效再生数等流行病学指标的变化,从而揭示新冠肺炎疫情多峰传播模式的动力学机制。
本研究发现,防控措施的时紧时松(或过早的解除干预措施)是导致二次暴发的重要因素之一。在新发突发传染病来临时,强有力的防控措施能很快的控制疫情,但同时也因为在较长时间内保护了易感人群,使其规模维持在易感人群规模阈值之上(即S∞ > Sth0),因而任何外来的感染病例必将导致疫情的二次暴发。实施防控措施越强的地区,在解除相关防控措施之前必须做好预案,否则二次暴发的风险和强度就越大。基于模型计算得到存在最优的控制措施使得第一波疫情后的易感者规模恰好在阈值水平处(S∞ = Sth0),这样外来的感染病例将无法导致疫情的再次暴发。另外,在逐步解除干预措施时,疫苗接种能起到补偿作用,能有效的避免疫情的二次暴发,特别是基于易感人群规模阈值,计算出了能够避免二次暴发的最优疫苗接种比率。这为疫苗的持续推进和干预措施的逐步解除提供了较好的思路。
感染者人数驱动的民众行为改变也很大程度地影响着疫情二次暴发风险。对疫情敏感程度较小时,越易出现较大的二次暴发,随着民众对疫情敏感程度的增强,多次暴发逐步减弱。特别是高敏感性(m值大)尽管维持了易感人群规模较长时间位于阈值水平之上,但能维持低水平的多次暴发,这说明在无疫苗或疫苗接种过程中,高效的常态化防控措施是非常有必要的。另外,疫苗的持续接种能有效的规避由于行为改变引起的疫情的暴发(接种率越高,峰值越小、高峰时间越早)。
疫苗接种的持续推进、感染者人数驱动的民众行为改变和干预措施的逐步解除等因素,综合影响和改变着疫情的发展趋势,3种因素不同强度的综合作用,使得世界各国疫情暴发的模式差异较大(疫情高峰的大小、来临的早晚、规模的大小等)。本研究发现,尽管引发世界各国疫情反复暴发的因素众多,且具有较强的随机性和不确定性,但影响我国新冠肺炎疫情的多次局部暴发、世界各国疫情的复杂发生模式的关键因素包括易感人群规模大小、干预措施实施的强弱及解除时间、疫苗接种率和时效性、疫情驱动个体行为的动态演化等核心因素,以及这些因素之间的协同效应。因此,根据我国各地区、世界各国的易感者规模阈值、干预措施强弱、民众行为改变对疫情的敏感性和疫苗接种能力等因素,设计符合当地实际的优化常态化防控策略,就能有效避免新冠肺炎疫情的多次暴发。
本研究存在局限性。一是只根据文献固定相关的参数,从模型上说明疫情出现多波峰的机制,但是如何量化疫情驱动的个体行为变化率,尚缺乏相关行为学数据和对模型进行辨识和参数估计的疫情数据,虽然这不影响对新冠肺炎疫情多次暴发的驱动机制的定性分析,但是影响了对民众行为变化定量的描述;二是在参数敏感性分析过程中,仅聚焦个体行为变化对疫情的敏感程度、干预强度和疫苗接种率这3个与疫情多次暴发密切相关的参数进行设定,未考虑疫苗接种前置时间、滞后效应、疫苗的保护率以及病毒变异等关键因素对疫情多次暴发的影响。为实现上述目标,后期需构建更完善的数学模型,包括融合行为学数据在内的多源数据,进行精细化的参数敏感性和不确定性分析。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
Korber B, Fischer WM, Gnanakaran S, et al. Tracking changes in SARS-CoV-2 spike:evidence that D614G increases infectivity of the COVID-19 virus[J]. Cell, 2020, 182(4): 812-827. DOI:10.1016/j.cell.2020.06.043 |
| [2] |
Grubaugh ND, Hanage WP, Rasmussen AL. Making sense of mutation:what D614G means for the COVID-19 pandemic remains unclear[J]. Cell, 2020, 182(4): 794-795. DOI:10.1016/j.cell.2020.06.040 |
| [3] |
国家卫生健康委员会[EB/OL].新型冠状病毒肺炎疫情最新情况[EB/OL].(2020-12-31)[2021-02-01].http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml. National Health Commission. The update situation of COVID-19 epidemic[EB/OL].(2020-12-31)[2021-02-01].http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml. |
| [4] |
WHO. WHO Coronavirus (COVID-19) Dashboard[EB/OL]. (2021-01-31)[2021-02-01]. https://covid19.who.int/.
|
| [5] |
Choi W, Shim E. Optimal strategies for vaccination and social distancing in a game-theoretic epidemiologic model[J]. J Theoret Biol, 2020, 505: 110422. DOI:10.1016/j.jtbi.2020.110422 |
| [6] |
Galanti M, Pei S, Yamana TK, et al. Social distancing remains key during vaccinations[J]. Science, 2021, 371(6528): 473-474. DOI:10.1126/science.abg2326 |
| [7] |
Tang B, Liu PY, Yang J, et al. The challenges of the coming mass vaccination and exit strategy in prevention and control of COVID-19, a modelling study[J]. medRxiv, 2021. DOI:10.1101/2020.12.18.20248478 |
| [8] |
Handel A, Longini IM, Antia R. What is the best control strategy for multiple infectious disease outbreaks?[J]. Proc Biol Sci, 2007, 274(1611): 833-837. DOI:10.1098/rspb.2006.0015 |
| [9] |
Poletti P, Ajelli M, Merler S. Risk perception and effectiveness of uncoordinated behavioral responses in an emerging epidemic[J]. Math Biosci, 2012, 238(2): 80-89. DOI:10.1016/j.mbs.2012.04.003 |
| [10] |
Tang SY, Xiao YN. One-compartment model with Michaelis-Menten elimination kinetics and therapeutic window:an analytical approach[J]. J Pharmacokinet Pharmacodyn, 2007, 34(6): 807-827. DOI:10.1007/s10928-007-9070-4 |
| [11] |
Tang B, Wang X, Li Q, et al. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions[J]. J Clin Med, 2020, 9(2): 462. DOI:10.3390/jcm9020462 |
| [12] |
Tang B, Xia F, Tang SY, et al. The effectiveness of quarantine and isolation determine the trend of the COVID-19 epidemics in the final phase of the current outbreak in China[J]. Int J Infect Dis, 2020, 95: 288-293. DOI:10.1016/j.ijid.2020.03.018 |
| [13] |
王霞, 唐三一, 陈勇, 等. 新型冠状病毒肺炎疫情下武汉及周边地区何时复工?数据驱动的网络模型分析[J]. 中国科学:数学, 2020, 50(7): 969-978. Wang X, Tang SY, Chen Y, et al. When will be the resumption of work in Wuhan and its surrounding areas during COVID-19 epidemic? A data-driven network modeling analysis[J]. Sci Sin Math, 2020, 50(7): 969-978. DOI:10.1360/SSM-2020-0037 |
| [14] |
唐三一, 唐彪, Bragazzi NL, 等. 新型冠状病毒肺炎疫情数据挖掘与离散随机传播动力学模型分析[J]. 中国科学:数学, 2020, 50(8): 1071-1086. Tang SY, Tang B, Bragazzi NL, et al. Analysis of COVID-19 epidemic traced data and stochastic discrete transmission dynamic model[J]. Sci Sin Math, 2020, 50(8): 1071-1086. DOI:10.1360/SSM-2020-0053 |
| [15] |
唐三一, 肖燕妮, 彭志行, 等. 新型冠状病毒肺炎疫情预测建模、数据融合与防控策略分析[J]. 中华流行病学杂志, 2020, 41(4): 480-484. Tang SY, Xiao YN, Peng ZH, et al. Prediction modeling with data fusion and prevention strategy analysis for the COVID-19 outbreak[J]. Chin J Epidemiol, 2020, 41(4): 480-484. DOI:10.3760/cma.j.cn112338-20200216-00107 |
| [16] |
Li Q, Guan XH, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia[J]. N Engl J Med, 2020, 382(13): 1199-1207. DOI:10.1056/NEJMoa2001316 |
| [17] |
Imai N, Cori A, Dorigatti I, et al. Report 3: Transmissibility of 2019-nCoV[EB/OL]. (2020-01-25). https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-transmissibility-25-01-2020.pdf.
|
| [18] |
Read JM, Bridgen JRE, Cummings DAT, et al. Novel coronavirus 2019-nCoV:early estimation of epidemiological parameters and epidemic predictions[J]. medRxiv, 2020. DOI:10.1101/2020.01.23.20018549 |
| [19] |
Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China:a modelling study[J]. Lancet, 2020, 395(10225): 689-697. DOI:10.1016/S0140-6736(20)30260-9 |
 2021, Vol. 42
2021, Vol. 42


